Лекция 4 - Простейшие СМО.ppt
- Количество слайдов: 33

Простейшие системы массового обслуживания и их характеристики Лекция 4

Характеристики СМО в стационарном режиме. Формулы Литтла Рассмотрим любую СМО и связанные с ней два потока событий: 1) поток заявок, прибывающих в СМО; 2) поток заявок, покидающих СМО. В стационарном режиме интенсивности обеих потоков равны: вх = вых = . Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2008, лекция 4 2

Пусть X(t) – число заявок, прибывших в СМО до момента t; Y(t) – число заявок, покинувших СМО до момента t. Для любого момента t можно определить Z(t) = X(t) – Y(t) - число заявок, находящихся в СМО. Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2008, лекция 4 3
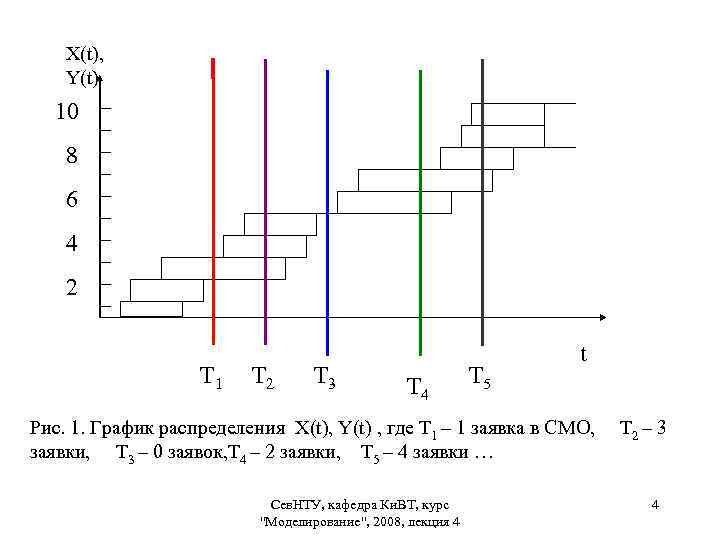
X(t), Y(t) 10 8 6 4 2 T 1 T 2 T 3 T 4 T 5 t Рис. 1. График распределения X(t), Y(t) , где Т 1 – 1 заявка в СМО, Т 2 – 3 заявки, Т 3 – 0 заявок, Т 4 – 2 заявки, Т 5 – 4 заявки … Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2008, лекция 4 4

Тогда среднее число заявок n, находящихся в СМО за промежуток времени Т (площадь фигуры, изображенной на рис. 1), можно определить по формулам: (1) или (2) где Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2008, лекция 4 5

Среднее число заявок, пришедших в СМО за время Т, определяется как Т. Тогда среднее время пребывания i заявок в системе: (3) Если в (3) , то справедливо (4) Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2008, лекция 4 6

В соответствии с (4) среднее число заявок в СМО определяется по 1 -ой формуле Литтла, т. е. (5) 1 -Я ФОРМУЛА ЛИТТЛА : для любой СМО, при любом характере потока заявок, при любом распределении времени обслуживания, при любой дисциплине обслуживания среднее время пребывания заявки в системе равно среднему числу заявок в системе, деленному на интенсивность потока заявок. Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2008, лекция 4 7

2 -Я ФОРМУЛА ЛИТТЛА: w - среднее время пребывания заявок в очереди L - среднее число заявок в очереди : Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2008, лекция 4 8

Среднее время пребывания заявки в CMO u = w + , (7) где w – среднее время ожидания в очереди; - среднее время обслуживания в приборе. Количество заявок в СМО n = L + R, (8) где L – среднее число заявок в очереди; R – среднее число заявок на обслуживании. Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2008, лекция 4 9

Простейшая СМО с отказами (задача Эрланга) Имеется N каналов (линий связи), на которые поступает простейший поток заявок с интенсивностью λ. Время обслуживания – экспоненциальное с интенсивностью μ, т. е. со средним значением υ = 1/ μ. Найти финальные вероятности состояний СМО, а также характеристики ее эффективности: 1) Ротк - вероятность отказа; 2) Рпрост – вероятность простоя; Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2008, лекция 4 10

Простейшая СМО с отказами (задача Эрланга) 3) Q – относительную пропускную способность, т. е. вероятность того, что заявка будет обслужена; 4) А – абсолютную пропускную способность, т. е. среднее число заявок, обслуживаемых в единицу времени; 5) R – среднее число занятых каналов. Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2008, лекция 4 11

Решение. М/М/N/0 Состояния системы будем нумеровать по числу заявок, находящихся в системе (в данном случае оно совпадает с числом занятых каналов): S 0 – в СМО нет ни одной заявки; S 1 –в СМО находится одна заявка ( занят один канал, остальные свободны); … Sk - в СМО находится k заявок ( занято k каналов, остальные свободны); … Sn - в СМО находится n заявок ( все n каналов заняты). Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2008, лекция 4 12

Граф состояний и переходов СМО: Уравнения Колмогорова в стационарном режиме: λ Р 0 = μ Р 1 (λ+ (N-1)μ) Рn-1 = λ Рn-2 + N μ РN (μ + λ) Р 1 = λ Р 0 + 2μ Р 2 … N μ РN = λ Рn-1 (λ + i μ) Рi = λ Рi-1 + (i +1) μ Рi+1 Р 0 + Р 1 + … + РN = 1 … Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2008, лекция 4 13

Финальные вероятности состояний (Формулы Эрланга): Р 0 = [ 1 + ρ2/ 2! + ρ3/ 3! +… + ρN/ N! ] – 1 , Рi = ρi/ i! * [ 1 + ρ2/ 2 + ρ3/ 3! +… + ρN/ N! ] -1 = ρi/ i! * Р 0 , (9) где ρ = λ/μ – приведенная интенсивность потока заявок - среднее число заявок, приходящее за время обслуживания одной заявки. Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2008, лекция 4 14

Характеристики эффективности: 1) Вероятность отказа (заняты все каналы) Ротк = РN = ρN/ N! * Р 0 , 2) Вероятность простоя Рпрост = Р 0 = [ 1 + ρ2/ 2! + ρ3/ 3! +… + ρN/ N! ]-1 , 3) Относительная пропускная способность: Q = 1 - Pотк = 1 - ρN/ N! * Р 0, 4) Абсолютная пропускная способность А = λ *Q = λ (1 - ρN/ N! * Р 0), 5) Среднее число занятых каналов R = 0*Р 0 + 1* Р 1 + … + N*РN = ρ (1 - ρN/ N! * Р 0). Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2008, лекция 4 15
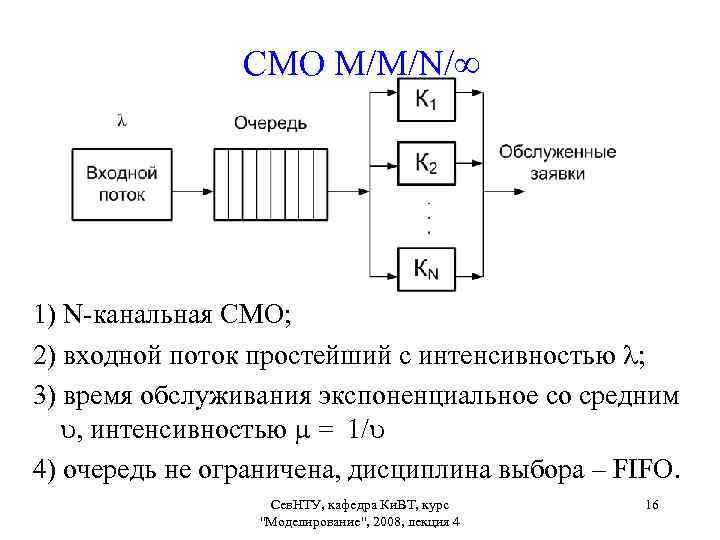
СМО M/M/N/ 1) N-канальная СМО; 2) входной поток простейший с интенсивностью ; 3) время обслуживания экспоненциальное со средним , интенсивностью = 1/ 4) очередь не ограничена, дисциплина выбора – FIFO. Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2008, лекция 4 16

. Состояния системы (СМО M/M/N/ ) Состояния системы нумеруются по числу заявок в системе: S 0 – в СМО заявок нет (все каналы свободны); S 1 - занят один канал, остальные свободны; … Sn - заняты все n каналов (очереди нет); Sn+1 - заняты все n каналов, одна заявка стоит в очереди; … Sn+к - заняты все n каналов, K заявoк стоит в очереди; … Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2008, лекция 4 17
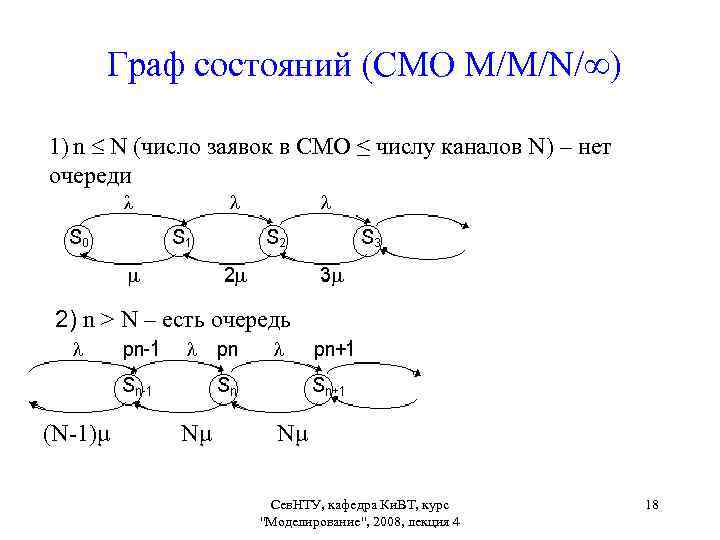
Граф состояний (СМО M/M/N/ ) 1) n N (число заявок в СМО ≤ числу каналов N) – нет очереди 2) n > N – есть очередь (N-1)μ Nμ Nμ Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2008, лекция 4 18

Условия существования стационарного режима: 1) ρ < 1, ρ – загрузка одного канала; 2) R < N, R - среднее число занятых каналов; 3) , υ – время обслуживания заявки; 4) ; 5) λ < μ N. Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2008, лекция 4 19

Решение системы уравнений Колмогорова: (Финальные вероятности) Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2008, лекция 4 20

М/М/N/∞ М/М/1/∞ 1) R – среднее число занятых каналов R=λ·ν = λ/ ρ = λ·ν = λ/ 2) Рпрост – вероятность простоя Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2008, лекция 4 21

М/М/N/∞ М/М/1/∞ 3) L- среднее число заявок в очереди 4) n – среднее число заявок в системе n = L + R Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2008, лекция 4 22

М/М/N/∞ М/М/1/∞ 5) w - среднее время пребывания заявки в очереди 6) u – среднее время пребывания заявки в системе Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2008, лекция 4 23

Пример1: железнодорожная касса М/М/2/ Два окошка общая очередь Билеты в пункты А и В λА = λВ = 0. 45 (пассажира в минуту) λ = λА + λВ = 0. 9 ν = 2 минуты ? две СМО М/М/1/∞ Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2008, лекция 4 24

Пример1: железнодорожная касса М/М/2/ R= λ ν = 1. 8 - ср. число занятых каналов ρ = R/2 = 0. 9 < 1 – стационарный режим существует. Вероятность простоя: Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2008, лекция 4 25

Пример1: железнодорожная касса М/М/2/ Среднее число пассажиров в очереди Среднее время пребывания пассажиров в очереди: Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2008, лекция 4 26

Пример1: железнодорожная касса две СМО М/М/1/∞ λ = 0, 45 пасс/мин, ν = 2 мин ρ = λ ν = 0, 9 < 1– стационарный режим существует Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2008, лекция 4 27
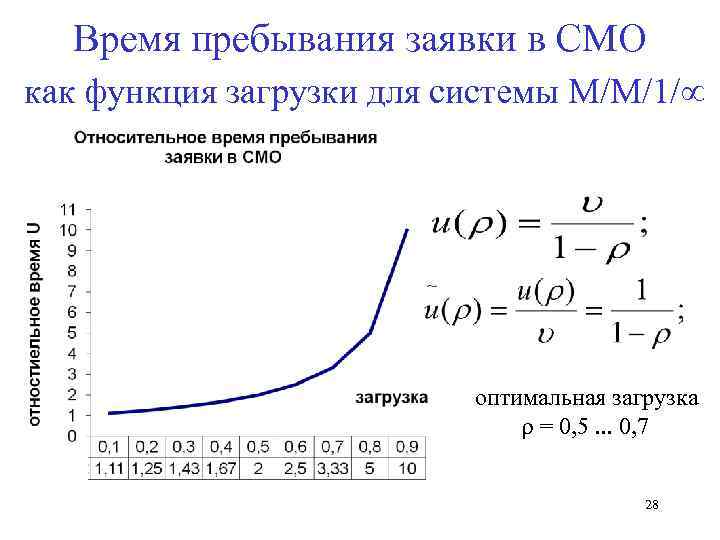
Время пребывания заявки в СМО как функция загрузки для системы М/М/1/ оптимальная загрузка = 0, 5. . . 0, 7 28

СМО М/М/1/ как модель обработки пакетов в сети с коммутацией пакетов Основные типы коммутации: 1. Коммутация каналов – абонентам сети выделяется зарезервированный канал передачи данных с фиксированной пропускной способностью и постоянной скоростью передачи данных. Используется для передачи потокового трафика реального времени (данные, чувствительные к задержкам – голос, видео). Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2008, лекция 4 29

М/М/1/ как модель обработки пакетов в сети с коммутацией пакетов Основные типы коммутации: 2. Коммутация пакетов – передаваемые пользователем данные разбиваются в исходном узле на сравнительно небольшие части, называемые пакетами (кадрами), затем передаются по сети независимо друг от друга и собираются в узле назначения Специально разработана для эффективной передачи компьютерного (пульсирующего) трафика Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2008, лекция 4 30
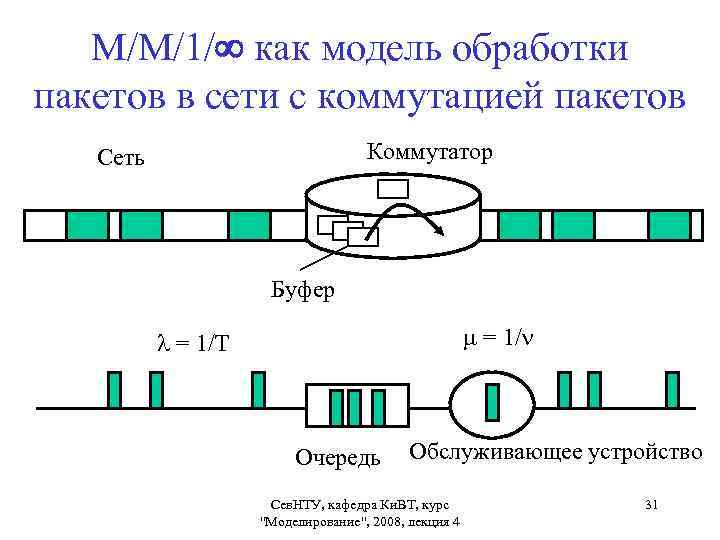
М/М/1/ как модель обработки пакетов в сети с коммутацией пакетов Коммутатор Сеть Буфер = 1/Т Очередь Обслуживающее устройство Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2008, лекция 4 31

М/М/1/ как модель обработки пакетов в сети с коммутацией пакетов 1. Входной поток заявок – поток пакетов, поступающих на вход интерфейса коммутатора. 2. Очередь – буфер входного интерфейса коммутатора. 3. Обслуживающее устройство – процессор, обрабатывающий пакеты и направляющий их на выходной интерфейс. 4. Среднее время обслуживания заявки – среднее время продвижения пакета процессором коммутатора из входного буфера в выходной канал. Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2008, лекция 4 32

М/М/1/ как модель обработки пакетов в сети с коммутацией пакетов Среднее время пребывания заявки в очереди как характеристика эффективности СМО: ρ – коэффициент использования (utilization) обслуживающего устройства (ресурса). Для обеспечения приемлемого уровня задержек в сети самый простой способ – работа в недогруженном режиме: все коммутаторы и каналы работают на 20 -30% от своей максимальной производительности: = 0, 2. . 0, 3 Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2008, лекция 4 33
Лекция 4 - Простейшие СМО.ppt