Пропозициональная логика Основы логики высказываний СУЖДЕНИЕ ВЫСКАЗЫВАНИЕ

Пропозициональная логика Основы логики высказываний

СУЖДЕНИЕ ВЫСКАЗЫВАНИЕ - предложение, выражающее определенное суждение ПРЕДЛОЖЕНИЕ – синтаксическая форма естественного языка СУЖДЕНИЕ – логическая форма мысли

Христианский пример (1. 2) Если некоторые граждане РФ – христиане, а все христиане празднуют Рождество, Значит, некоторые граждане РФ празднуют Рождество (1. 1) Все христиане празднуют Рождество Некоторые граждане РФ – христиане Некоторые граждане РФ празднуют Рождество

Иудейский пример (2. 1) Христиане празднуют Рождество, и не празднуют Хануку, а в этой стране празднуют Хануку, и не празднуют Рождество, значит, в этой стране христиане не живут. Хр. Х) (Стр. Х Стр. Р) ЖХр 2. 2. (Хр. Р (2. 3) Хр а Р Хр е Х Стр а Х Стр е Р Стр е Хр

Коран-пример (3. 1) Если ваши книги согласны с Кораном, то они излишни. Если ваши книги не согласны с Кораном, то вредны. Если ваши книги излишни или вредны, то их следует уничтожить. Следовательно, ваши книги следует уничтожить. p q p r (r q) s s

Логическое следование n Отношение между логическими формами высказываний Из Г логически следует В, если и только если при любой интерпретации параметров в составе Г и В, при которой все выражения из Г принимают значение "истина", выражение В также примет значение "истина"

Дедуктивная логика n n выделение и систематизация класса логических законов выделение и систематизация форм правильных умозаключений (таких умозаключений, в которых заключения логически следуют из посылок)

Логическая теория n n n Язык логической теории (определение формального языка) + правило построения формул (определение правильно построенной формулы) Синтаксис логической теории (правила получения формул одних формул из других) Семантика логической теории (правила приписывания значений формулам)

Логические теории n n строятся в рамках формализованных языков решают следующие задачи 1) выделяют во множестве формул языка класс формул, представляющих собой логические законы, 2) выделяют во множестве переходов (от формул F 1, F 2, … Fn к формуле Q) F 1, F 2, … F n Q класс таких переходов, которые являются формами правильных умозаключений, т. е. в которых формула Q логически следует из F 1, F 2, … Fn

Язык логической теории n n n логические символы — специальные знаки для логических терминов, нелогические символы — параметры, предназначенные для замещения простых высказываний или нелогических терминов различных категорий, технические символы (скобки).

ВЫСКАЗЫВАНИЕ n n предложение, выражающее суждение ЭЛЕМЕНТАРНЫЕ ВЫСКАЗЫВАНИЯ - не содержащие логических постоянных n СЛОЖНЫЕ ВЫСКАЗЫВАНИЯ - высказывания, которые содержат логические постоянные n ФОРМЫ ВЫСКАЗЫВАНИЙ - неполные высказывания, которые содержат предметные переменные

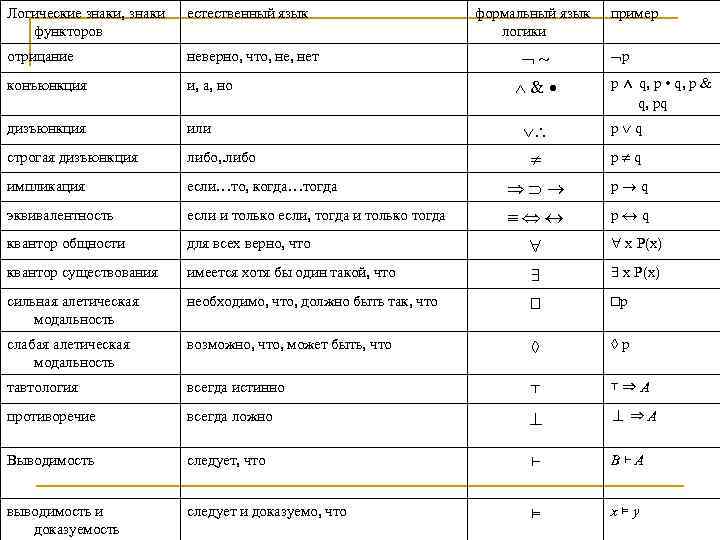Логические знаки, знаки функторов естественный язык отрицание неверно, что, нет конъюнкция и, а, но дизъюнкция или строгая дизъюнкция либо, . либо импликация формальный язык логики пример р p ⋀ q, p • q, p & q, pq p q если…то, когда…тогда p q эквивалентность если и только если, тогда и только тогда p q квантор общности для всех верно, что х Р(х) квантор существования имеется хотя бы один такой, что х Р(х) сильная алетическая модальность необходимо, что, должно быть так, что р слабая алетическая модальность возможно, что, может быть, что р тавтология всегда истинно ⊤ ⊤⇒A противоречие всегда ложно ⊥⇒A Выводимость следует, что ⊢ B⊢A выводимость и доказуемость следует и доказуемо, что ⊨ x⊨y

Язык логики высказываний ПРОПОЗИЦИОНАЛЬНЫЕ БУКВЫ (пропозициональные переменные): р, q, r, s, t, p 1, q 1, r 1, s 1, t 1, p 2, q 2, … 2. ЛОГИЧЕСКИЕ ЗНАКИ (логические союзы): 1. ~ отрицание; конъюнкции; дизъюнкции; импликации; эквивалентности, строгой дизъюнкции. ТЕХНИЧЕСКИЕ ЗНАКИ: ( ) , . 4. Никаких других знаков в языке логики высказываний нет. 3.

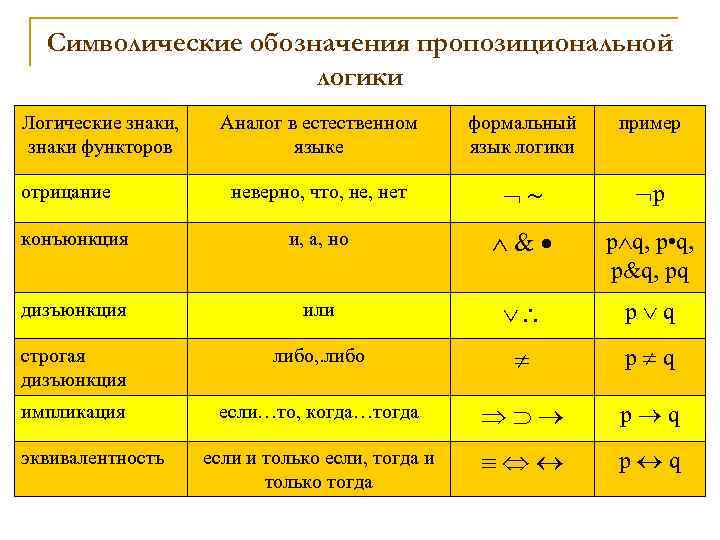Символические обозначения пропозициональной логики Логические знаки, знаки функторов Аналог в естественном языке формальный язык логики пример неверно, что, нет р конъюнкция и, а, но p q, p • q, p&q, pq дизъюнкция или p q строгая дизъюнкция либо, . либо p q импликация если…то, когда…тогда p q если и только если, тогда и только тогда p q отрицание эквивалентность

Формула логики высказываний 1. Пропозициональная переменная есть формула; 2. Если А — произвольная формула, то ~А— тоже формула; 3. Если А и В — произвольные формулы, то (А В), (A B); (А В), (А В) — тоже формулы. 4. Никаких других формул, кроме указанных в пп. 1 — 3 , в языке логики высказываний нет.

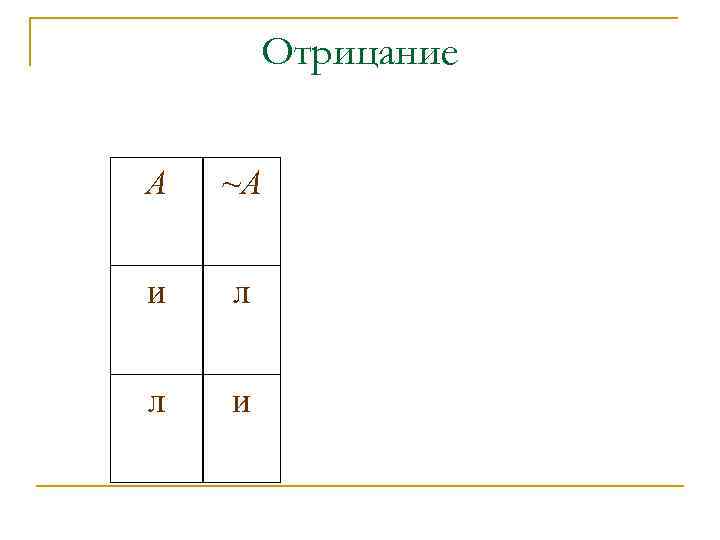Отрицание А ~А и л л и

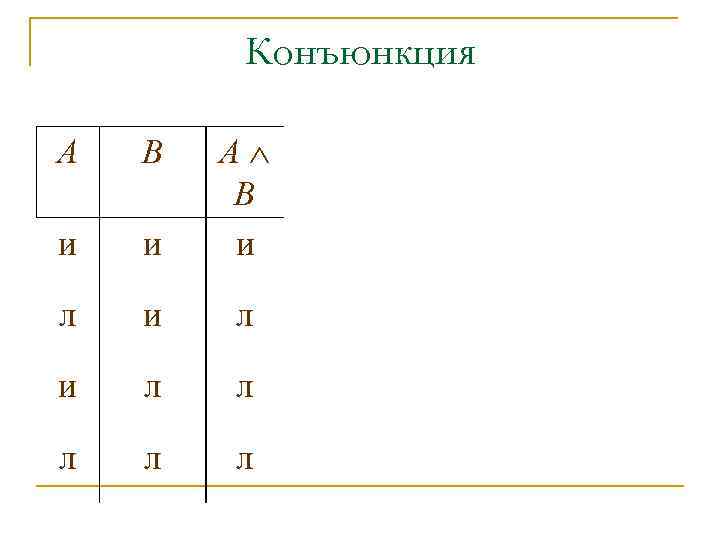Конъюнкция А B и и А В и л и л л л

Дизъюнкция А В A B и и и л и л л л

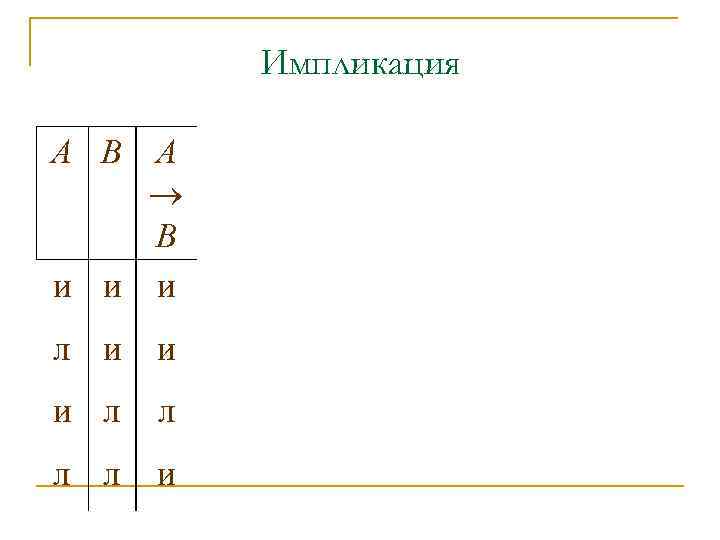Импликация А В А В и и и л л л л и

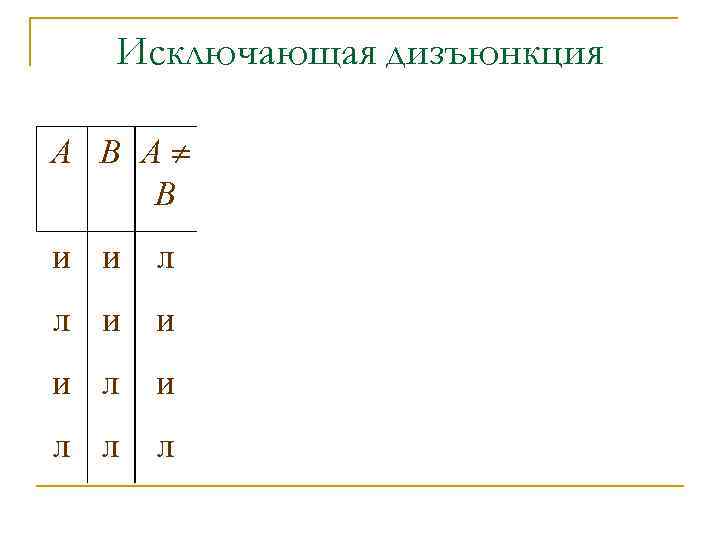Исключающая дизъюнкция А В и и л л и и и л л л

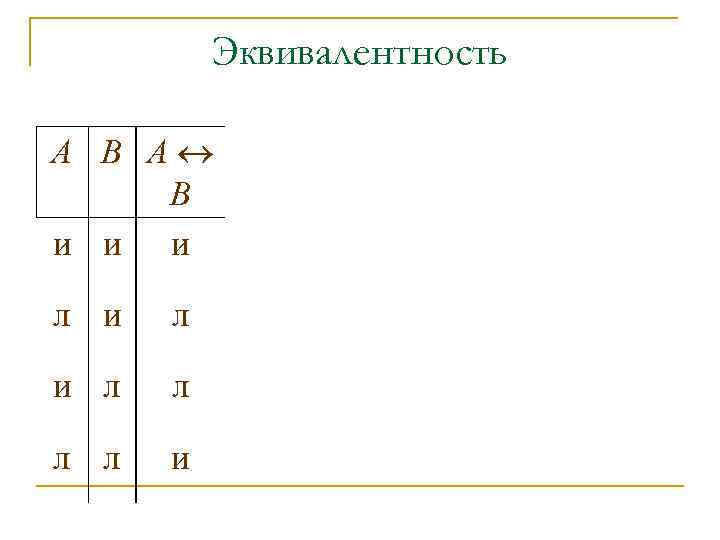Эквивалентность А В и и и л и л л и

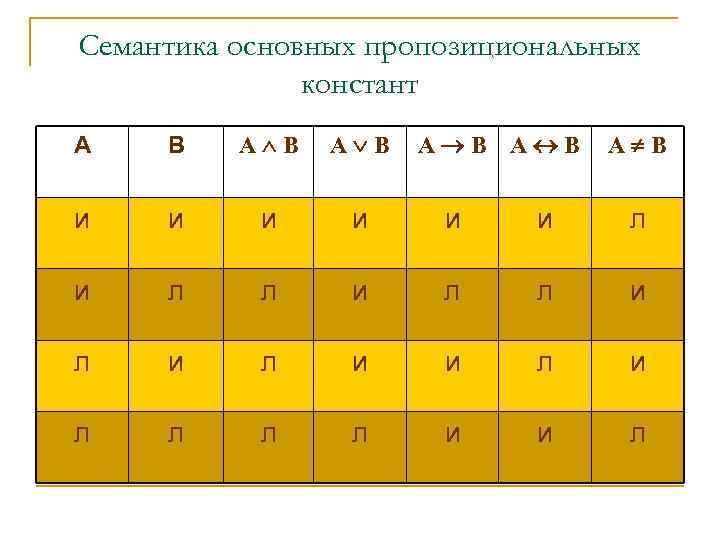Семантика основных пропозициональных констант А В A B А В А В и и и л и л и и л л л л и и л

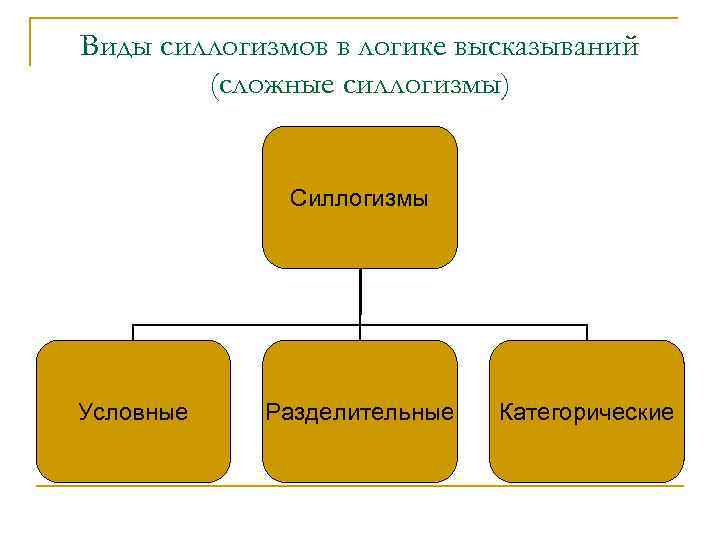Виды силлогизмов в логике высказываний (сложные силлогизмы) Силлогизмы Условные Разделительные Категорические

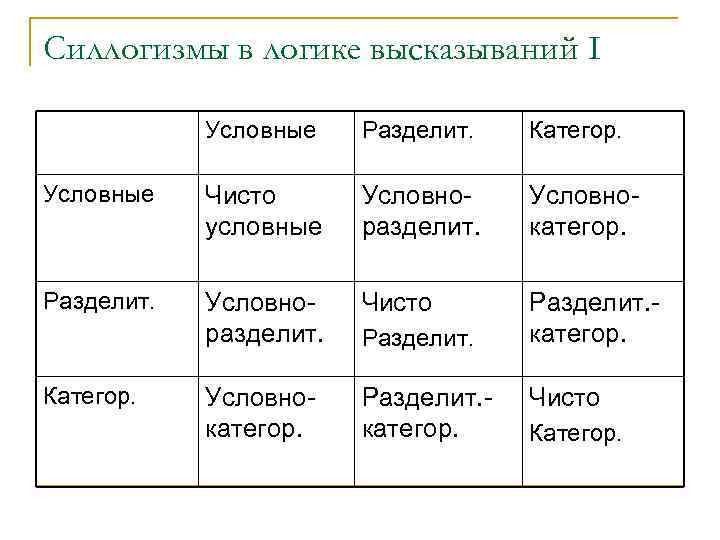Силлогизмы в логике высказываний I Условные Разделит. Категор. Условные Чисто условные Условноразделит. Условнокатегор. Разделит. Условноразделит. Чисто Разделит. категор. Условнокатегор. Разделит. категор. Категор. Разделит. Чисто Категор.

Силлогизмы в логике высказываний II Условные Разделит. Категор. Условные А В В С С А А В C А В B А Разделит. А В C (В C) А А В A B А В В С С В А А В А B А В C А C B Ма. Р Si. М Si. P Категор.

Чисто условные силлогизмы I Если бояться волков, то в лес не ходить. Если в лес не ходить, то грибов не видать. Если бояться волков, то грибов не видать. Если ваши книги согласны с Кораном, то они излишни. Если ваши книги излишни, то они вредны. Если ваши книги согласны с Кораном, то они вредны

Чисто условные силлогизмы II Если ваши книги согласны с Кораном, то они вредны. Если ваши книги вредны, то их следует уничтожить Если ваши книги согласны с Кораном, то их следует уничтожить p q, q r p r

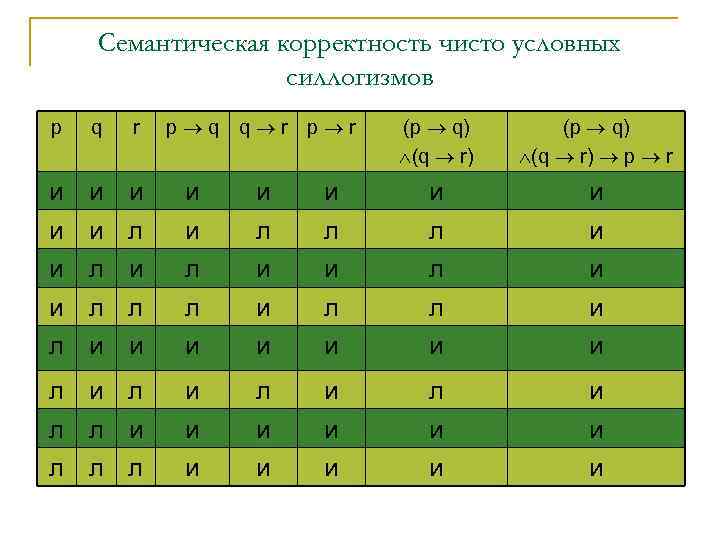Семантическая корректность чисто условных силлогизмов p q r p q q r p r (p q) (q r) p r и и и л и л и и л л и и л л л и и и л л л и и и и и л и и и

Пример сложного чисто условного силлогизма (Если) не было гвоздя — подкова пропала, (если) не было подковы, лошадь захромала, командир убит, (командир убит), конница разбита, (конница разбита, ) армия бежит, (армия бежит, ) враг вступает в город, (враг вступает в город, ) пленных не щадя, оттого, что в кузнице не было гвоздя.

Условно-категорический силлогизм Если в этой стране официально празднуют Хануку, значит в этой стране иудаизм – господствующая религия В этой стране официально празднуют Хануку Значит, в этой стране иудаизм – господствующая религия. Если в этой стране официально празднуют Рождество, значит в этой стране христианство – господствующая религия Неверно, что в этой стране христианство – господствующая религия Значит, неверно, что в этой стране официально празднуют Рождество

Модусы условно-категорического силлогизма I Если в этой стране официально празднуют Хануку, значит в этой стране иудаизм – господствующая религия В этой стране официально празднуют Хануку Значит в этой стране иудаизм – господствующая религия. Modus ponens А В A B

Модусы условно-категорического силлогизма II Если в этой стране официально празднуют Рождество, значит в этой стране христианство – господствующая религия Неверно, что в этой стране христианство – господствующая религия Значит, неверно, что в этой стране официально празднуют Рождество Modus tollens А В B А

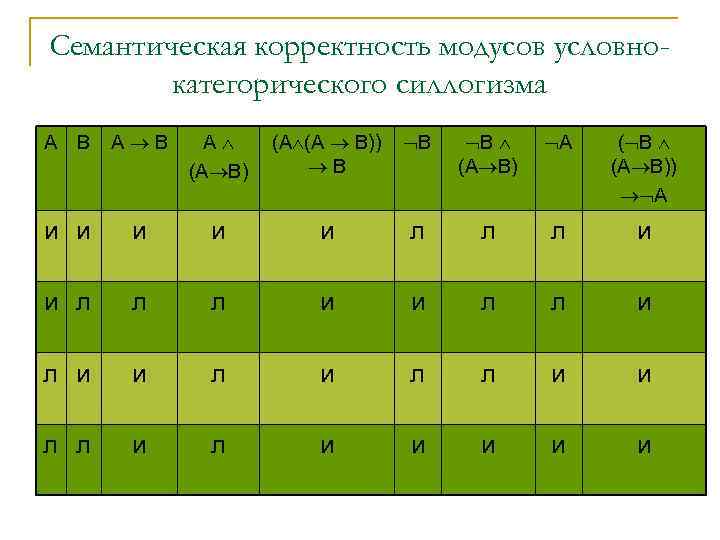Семантическая корректность модусов условнокатегорического силлогизма A B А В A (А В) (A (А В)) В В В (А В) A ( В (А В)) A и и и л л л и и л л и и и

Чисто разделительный силлогизм В этой стране празднуют Рождество или Хануку В этой стране празднуют Хануку или Рамадан Байрам Значит, в этой стране празднуют Рождество или Хануку или Рамадан Байрам А В В С С В А

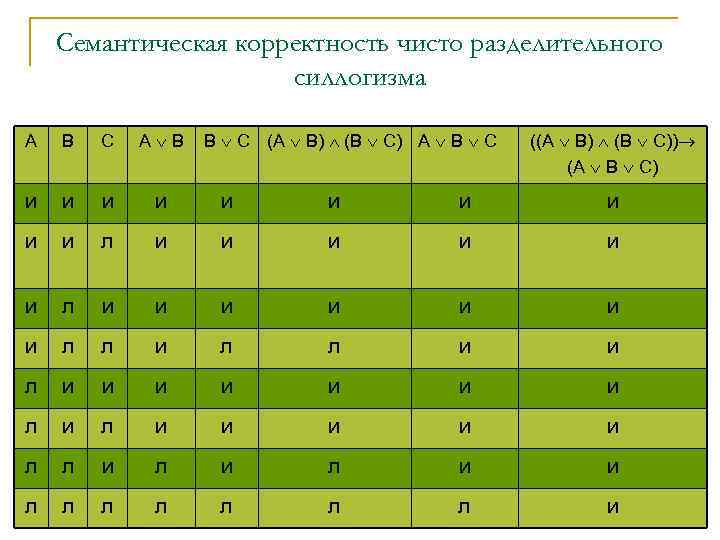Семантическая корректность чисто разделительного силлогизма А В С А В В С (А В) (В С) А В С ((А В) (В С)) (А В С) и и и и и л и и и и л л и и и и л и и и л л и л и и л л л л и

Разделительно-категорический силлогизм Ваши книги излишни или вредны. Ваши книги вредны. Значит, неверно, что ваши излишни. А В В А modus ponendo tollens Ваши книги излишни или вредны. Неверно, что ваши книги вредны. Значит, ваши книги излишни. А В В А мodus tollendo ponens

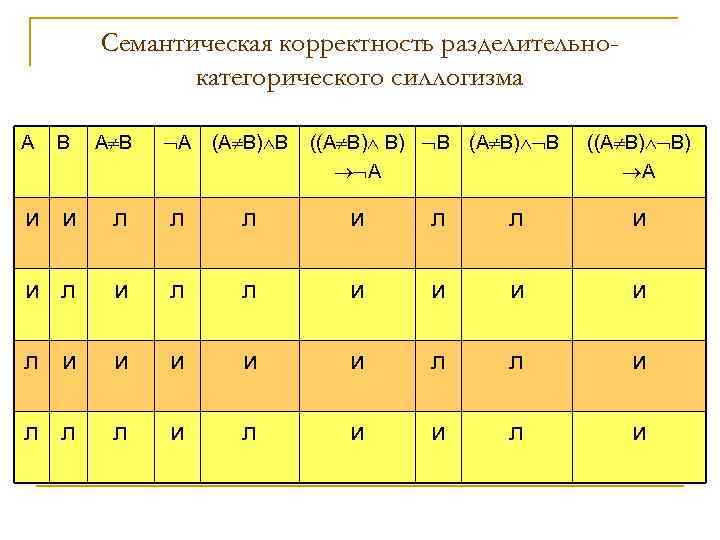Семантическая корректность разделительнокатегорического силлогизма А (А В) В л л л и и и и и л л л и и л и А В и и ((А В) В) В (А В) В А ((А В) В) А

Условно-разделительный (лемматический) силлогизм Если волк проголодался, он хочет поймать зайца, если лиса проголодалась, она хочет поймать зайца Если волк или лиса проголодались Зайца хотят поймать. Если удав спит, он сыт, если удав голоден, у него плохое настроение Удав спит или голоден Он сыт или у него плохое настроение. Если удав спит, то он сыт или устал Он не сыт и не устал Он не спит. Если удав сыт, он спит, если попугай рассуждает, у него хорошее настроение. Удав не спит и у попугая нет хорошего настроения Удав не сыт и попугай не рассуждает.

Модусы условно-разделительного (лемматического) силлогизма Простая конструктивная дилемма (А C) (В C) А В C (А В) (А C) (В C) А Простая деструктивная дилемма Сложная конструктивная дилемма (А C) (В D) А В C D (А В) (D C) (В C) (А D) Сложная деструктивная дилемма