ПРОПОЗИЦІЙНА ЛОГІКА Пропозиційний рівень розгляду не проникаємо у

ПРОПОЗИЦІЙНА ЛОГІКА Пропозиційний рівень розгляду: не проникаємо у внутрішню, суб’єктнопредикатну структуру висловлень та предикатів. Предикати – функції вигляду Р : А {T, F}, де А - абстрактна множина (її елементи неструктуровані) Засобами утворення складніших висловлень чи предикатів із простіших є логiчнi операцiї (композиції), які не враховують стуктурованості даних - пропозиційні композиції, або логiчнi зв’язки. Основні логічні зв’язки: – заперечення – диз’юнкцiя – кон’юнкцiя & – iмплiкацiя – еквiваленцiя – роздільна диз’юнкцiя 1

Логічні зв’язки відповідають певним зворотам природної мови. Заперечення: "не …", "невірно, що …". Диз’юнкцiя: "… або …". Кон’юнкцiя: "… та …", "… і …". Імплікація: "якщо … то …", "із. . . випливає. . . ". Еквiваленцiя: ". . . тоді і тільки тоді, коли. . . ", "… рівносильне …", "… еквівалентне …". Роздільна диз’юнкцiя: "або …, або …". Природна мова неоднозначна: – слово "коса" – речення "Микола зустрів Галю на лузі з квітами" Багатозначність "або": Чергові збори відбудуться завтра або післязавтра роздільна диз’юнкцiя Трикутник АВС прямокутний або рівнобедренний нероздільна диз’юнкцiя АВ=ВС, або трикутник АВС рівнобедрений еквіваленція 2

Для точного дослiдження предикатів та висловлень треба ввести строгу логіко-математичну мову. На пропозиційному рівні вводимо мову логiки висловлень, або мову пропозиційної логіки (мова ПЛ). Вимога до множини B базових пропозиційних композицій – повнота: B визначає клас усіх пропозиційних композицій (див. th Поста). Беремо множину базових композицій (логiчних зв’язок) { , }. Поширені варiанти мови ПЛ із множинами базових композицій { , }, { , &}, { , , &} та { , , &, }. При зафіксованій множині базових композицій мови ПЛ можуть відрізнятися способами запису пропозиційних формул. Префіксна (польська) форму запису: символ логічної операцiї (композиції) передує аргументам. Запропонував Я. Лукасєвiч (1878– 1956). 3

Пропозиційні композиції Предикати (P), (P, Q), &(P, Q), (P, Q) позначимо P, P Q, P&Q, P Q. Композиції та – базовi пропозиційнi композиції. Композиції , &, та – похіднi Враховуємо частковість предикатів. Так визначені логiчні зв’язки – Клінієві. ( P)(d) = T P(d) = F ( P)(d) = F P(d) = T в усіх інших випадках ( P)(d) (P Q)(d) = T P(d) = T або Q(d) = T (P Q)(d) = F P(d) = F та Q(d) = F в усіх інших випадках (P Q)(d) 4

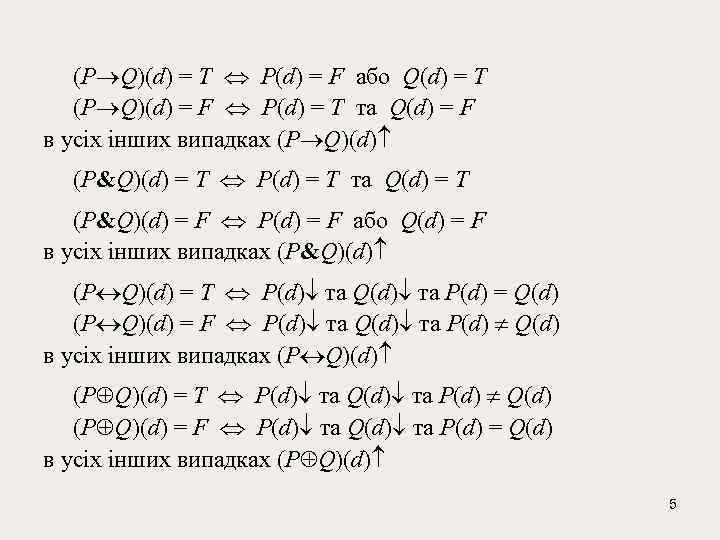(P Q)(d) = T P(d) = F або Q(d) = T (P Q)(d) = F P(d) = T та Q(d) = F в усіх інших випадках (P Q)(d) (P&Q)(d) = T P(d) = T та Q(d) = T (P&Q)(d) = F P(d) = F або Q(d) = F в усіх інших випадках (P&Q)(d) (P Q)(d) = T P(d) та Q(d) та P(d) = Q(d) (P Q)(d) = F P(d) та Q(d) та P(d) Q(d) в усіх інших випадках (P Q)(d) = T P(d) та Q(d) та P(d) Q(d) (P Q)(d) = F P(d) та Q(d) та P(d) = Q(d) в усіх інших випадках (P Q)(d) 5

Основні властивості логічних зв’язок 1) Комутативність та &: P Q = Q P; P&Q = Q&P. 2) Асоціативність та &: (P Q) R = P (Q R); (P&Q)&R = P&(Q&R). 3) Дистрибутивність відносно & та & відносно : (P Q)&R = (P&R) (Q&R); (P&Q) R = (P R)&(Q R). 4) Ідемпотентність та &: Р Р = Р; Р&Р = Р. 5) Закони поглинання: Р& (P Q) = Р; P (P&Q) = Р. 6) Зняття подвійного заперечення P = Р. 6

7) Закони де Моргана: (P Q) = ( P)&( Q); (P&Q) = ( P) ( Q). 8) Закон контрапозицiї: (P Q) = (( Q) ( P)). 9) Закон (правило) modus ponens P&(P Q) Q. 10) Зведення , та до , та &: P Q = ( P) Q ; P Q = (P Q)&(Q P) = (P&Q) (( P) &( Q)); P Q = (P Q) = ( (P Q)) ( (Q P)) = (P&( Q)) (( P)&Q). 11) Комутативність та : P Q = Q P; P Q = Q P. 12) Асоціативність та : (P Q) R = P (Q R); (P Q) R = P (Q R). 7

Мова пропозиційної логіки Мови ПЛ відрізняються – наборами символів базових логічних зв’язок – способами запису пропозиційних формул. Вибрали { , } та префіксну форму запису. Алфавiт мови ПЛ: – символи логiчних зв’язок і – множини Ps пропозицiйних символів. Визначення пропозиційної формули (ПФ): 1) кожний А Ps є ПФ; такі ПФ атомарні; 2) якщо та є ПФ, то та є ПФ. Множину всіх ПФ позначимо Fр. Формули в iнфiкснiй формi вважаємо скороченнями ПФ. 8

Приклад. ( ) - скорочення “справжньої” Ф. & – скорочення ПФ – скорочення ПФ . Прiоритет символiв логiчних зв’язок: , &, , . Вводимо правило розставлення дужок справа наліво Приклад. A B C A D означає A (B (C (( A) D))). 9

Інтерпретація ПФ за допомогою істиннісних оцінок. Iстиннiсна оцiнка мови ПЛ – довiльне : Ps {T, F}. Продовжимо до : Fр {T, F}: ( Ф)=T (Ф)=F; ( Ф )=T (Ф)=T або ( )=T. Кожна ПФ з множиною пропозиційних імен Х задає Х-арну функцiю на 2 елементнiй множинi {T, F}, тобто булеву функцiю. Кожна Х-арна булева функцiя задається деякою ПФ, причому для фiксованої булевої функцiї множина таких ПФ нескiнченна. Ф тавтологія, якщо (F) = T при кожнiй iстиннісній оцiнцi . Ф тавтологiя, якщо вона iстинна на кожному наборi значень її пропозицiйних імен. Тавтологiї називають законами пропозиційної логiки Ф суперечність, якщо (Ф) = F при кожнiй iстиннiснiй оцiнцi . Ф суперечність, якщо вона хибна на кожному наборi значень її пропозицiйних iмен. тавтологiя суперечнiсть. 10

Основні закони традиційної логіки виражають тавтології: - закон тотожності P P; - закон виключеного третього ( P) P; - закон несуперечливості (P&( P)). Властивості пропозиційних композицій. 1) Закони комутативності для та &: P Q Q P; P&Q Q&P; 2) Закони асоціативності та &: (P Q) R P (Q R); (P&Q)&R P&(Q&R); (P Q) R P (Q R). 3) Закони дистрибутивності для та &: (P Q)&R (P&R) (Q&R); (P&Q) R (P R)&(Q R). 4) Закони ідемпотентності для та &: Р Р Р; Р Р&Р. 11

5) Закони поглинання: Р&(P Q) Р; P (P&Q) Р. 6) Закон зняття подвійного заперечення: P Р. 7) Закони де Моргана: (P Q) ( P)&( Q); (P&Q) ( P) ( Q). 8) Закон контрапозицiї: ( ) ( ). 9) Закони комутативності та : (P Q) (Q P); (P Q) (Q P). 10) Закони асоціативності та : (P Q) R = P (Q R); (P Q) R = P (Q R). 12

Властивості ПФ та відношення на множині ПФ Мн-на ПФ { 1, . . . , n} суперечлива: 1&…& n – суперечність. На множинi ПФ введемо вiдношення: – логiчного (тавтологiчного) наслiдку ╞ ; – логiчної (тавтологiчної) еквiвалентностi т. є логiчним наслiдком , якщо – тавтологiя. та логiчно еквiвалентнi, якщо ╞ та ╞ . Позначення: ╞ т Замість ╞ пишемо ╞ . є логiчним наслiдком множини ПФ { 1, . . . , n}, якщо 1&…& n╞ . Позначення: { 1, . . . , n}╞ Основнi властивостi вiдношень ╞ та т. 1) ╞ рефлексивне і транзитивне 2) т рефлексивне, транзитивне і симетричне 3) тавтологія ╞ 4) т ╞ тавтологiя. 13

Теорема (семантичної еквiвалентностi). Нехай ' отримана iз замiною деяких входжень формул 1, . . . , n на 1, . . . , n вiдповiдно. Якщо 1 т 1, . . . , n т n, то т '. Інтерпретація ПФ на пропозиційних композиційних системах При зафіксованій мн-ні композицій C пропозиційна композиційна система (А, Pr, C) однозначно визначається об'єктом (А, Pr ). Такі об'єкти – абстрактні алгебраїчні системи (ААС) При зафіксованій множині базових композицій інтерпретація ПФ на семантичних моделях ПЛ є інтерпретацією ПФ на ААС (А, Pr ). Відображення інтерпретації атомарних формул I : Ps Pr задає базові предикати ААС (А, Pr ). Інтерпретаціями мови ПЛ природно вважати об'єкти ((A, Pr), I) Це – ААС з доданими ПС. Позначення: A=(A, I). 14

Відображення інтерпретації J : Fр Pr визначається за допомогою I. 1. J(В)=I(В) для кожного В Ps. 2. Нехай J( ) = P. Тодi J( )= P. 3. Нехай J( )=P та J( ) = Q. Тодi J( ) =P Q. Предикат J( ) – це значення формули при інтерпретації A=(A, I) J( ) будемо позначати A. Формула істинна при інтерпретації A=(A, I), або A-істинна, якщо A – істинний предикат. Це позначаємо A |=. Формула iстинна, якщо iстинна при кожнiй iнтерпретацiї. Пропозиційна формула iстинна тавтологія. Інтерпретації за допомогою істиннісних оцінок та на ААС еквівалентні 15

Пропозиційне числення Аксіоматичні системи, базовані на понятті ФС – гільбертівського типу Такі акс. системи для ПЛ – пропозиційні числення (числення висловлень) Пропозиційне числення (ПЧ) – це ФС (L, Ax, P) L – мова ПЛ Ax – множина аксіом ПЧ P – множина правил виведення ПЧ. Ax задається єдиною схемою аксiом . Це пропозицiйні аксiоми Множина ПВ P: П 1) |- - правило розширення. П 2) |- - правило скорочення. П 3) ( X) |- ( ) X - правило асоціативності. П 4) , X |- X - правило перетину. Теорема ПЧ – ПФ, яка виводиться із пропозиційних аксiом за допомогою ПВ П 1–П 4. Те, що ПФ - теорема, позначимо |-. Рiзнi варiанти ПЧ можуть вiдрiзнятися мовами та наборами аксiом i ПВ 16

Приклади виведень в ПЧ Тeорeма 1. Якщо |-A B, то |-B A. |-A B за прип. , |- A A як аксiома, тому |-B A за П 4. Тeорeма 2. Якщо |-A та |-A B, то |-B. |-A за прип. , |-B A за П 1, звiдки |-A B. За прип. |-A B, тобто |- A B, тому |-B B за П 4, звiдки |-B за П 2. Тeорeма 3. Якщо |-A 1, . . . , |-An та |-A 1. . . An B, то |-B. Застосуємо п раз теорему 2. Твердження теорем 1 та 2 трактуємо як похiднi ПВ: A B |-B A - правило комутативностi (ПК); A, A B |-B - правило modus ponens (МР). 17

Тeорeма 4. Якщо |-(A B) C, то |-A (B C). Із |-(A B) C за ПК |-C (A B), звiдки |-(C A) B за П 3. Далi |-B (C A) за ПК та |-(B C) A за П 3. Тепер за ПК |A (B C). Тeорeма 5. Якщо |-A B, то |- A B. Маємо |- A A (аксiома), тому |- A A за ПК. Звiдси та з умови |-A B за П 4 |-B A, тому |- A B за ПК. Висновки П 1–П 4 є тавтологiчними наслiдками засновкiв Пропозиційна аксіома тавтологія, тому кожна теорема ПЧ тавтологія. Отже, має місце тeорeма коректності ПЛ. Тeорeма 6. Кожна теорема ПЧ є тавтологiя. 18

Повноту ПЛ дає тeорeма тавтології (ТТ): Тeорeма 7 (тeорeма тавтології). Кожна тавтологiя є теоремою. Тeорeма тавтології для ПЧ. теорема тавтологiя Наслiдок. Якщо { 1, . . . , n}╞ та |- 1, . . . , |- n , то |-. Якщо { 1, . . . , n}╞ , то 1. . . n - тавтологiя за ТТ | 1. . . n . Згідно |- 1, . . . , |- n |- за теоремою 3. Окремі наслідки ТТ: 1) |-A&B |-A та |-B. 2) |-A B |- B A. 3) Якщо |-A B та |-B C, то |-A C. 4) |-A B та |-B A. 5) Якщо |-A B, то ( |-A |-B ). ТТ засвідчує адекватнiсть семантичної та синтаксичної iстинностi, тобто повноту логiчних засобiв ПЧ. 19

Із ТТ випливає несуперечливість ПЧ: не iснує ПФ A такої, що |-A та |- A На основі ТТ – розв’язність ПЧ: Тeорeма 8. Множина теорем ПЧ алгоритмiчно розв’язна вiдносно множини всiх ПФ. Алгоритм розв’язку. За даною ПФ A із п проп. іменами будуємо задану нею булеву функцiю f. Тодi ╞ A f є константа 1 За ТТ ╞ A |–A, тому для перевiрки |–A треба перевiрити, чи f є константа 1. Для цього обчисл. значення f на кожному iз 2 п наборiв значень її імен 20