Propositional Logic or how to reason correctly Chapter

Propositional Logic or how to reason correctly Chapter 8 (new edition) Chapter 7 (old edition)

Goals • Feigenbaum: In the knowledge lies the power. Success with expert systems. 70’s. • What can we represent? – Logic(s): Prolog – Mathematical knowledge: mathematica – Common Sense Knowledge: Lenat’s Cyc has a million statement in various knowledge – Probabilistic Knowledge: Bayesian networks • Reasoning: via search

History • 300 BC Aristotle: Syllogisms • Late 1600’s Leibnitz’s goal: mechanization of inference • 1847 Boole: Mathematical Analysis of Logic • 1879: Complete Propositional Logic: Frege • 1965: Resolution Complete (Robinson) • 1971: Cook: satisfiability NP-complete • 1992: GSAT Selman min-conflicts

Syllogisms • Proposition = Statement that may be either true or false. • John is in the classroom. • Mary is enrolled in 270 A. • If A is true, and A implies B, then B is true. • If some A are B, and some B are C, then some A are C. • If some women are students, and some students are men, then ….

Concerns • What does it mean to say a statement is true? • What are sound rules for reasoning • What can we represent in propositional logic? • What is the efficiency? • Can we guarantee to infer all true statements?

Semantics • • Model = possible world x+y = 4 is true in the world x=3, y=1. x+y = 4 is false in the world x=3, y = 1. Entailment S 1, S 2, . . Sn |= S means in every world where S 1…Sn are true, S is true. • Careful: No mention of proof – just checking all the worlds. • Some cognitive scientists argue that this is the way people reason.

Reasoning or Inference Systems • Proof is a syntactic property. • Rules for deriving new sentences from old ones. • Sound: any derived sentence is true. • Complete: any true sentence is derivable. • NOTE: Logical Inference is monotonic. Can’t change your mind.

Proposition Logic: Syntax • See text for complete rules • Atomic Sentence: true, false, variable • Complex Sentence: connective applied to atomic or complex sentence. • Connectives: not, and, or, implies, equivalence, etc. • Defined by tables.

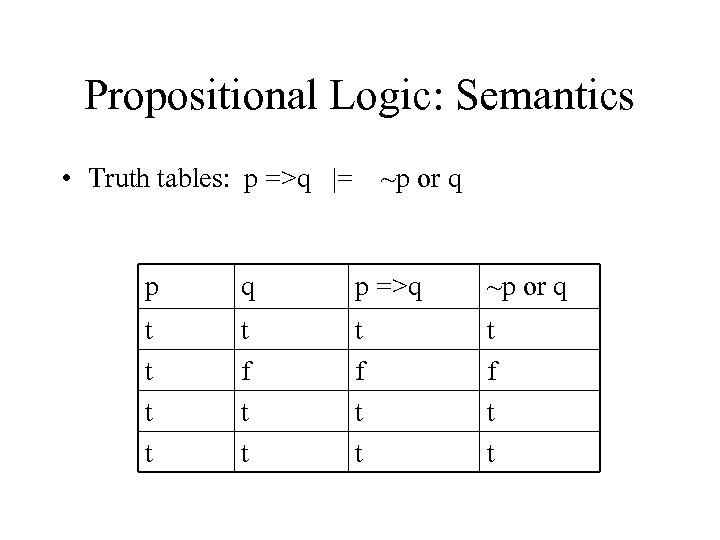Propositional Logic: Semantics • Truth tables: p =>q |= ~p or q p =>q ~p or q t t t f t t

Implies => • If 2+2 = 5 then monkeys are cows. TRUE • If 2+2 = 5 then cows are animals. TRUE • Indicates a difference with natural reasoning. Single incorrect or false belief will destroy reasoning. No weight of evidence.

Inference • • Does s 1, . . sk entail s? Say variables (symbols) v 1…vn. Check all 2^n possible worlds. In each world, check if s 1. . sk is true, that s is true. • Approximately O(2^n). • Complete: possible worlds finite for propositional logic, unlike for arithmetic.

Translation into Propositional Logic • If it rains, then the game will be cancelled. • If the game is cancelled, then we clean house. • Can we conclude? – If it rains, then we clean house. • p = it rains, q = game cancelled r = we clean house. • If p then q. not p or q • If q then r. not q or r • if p then r. not p or r (resolution)

Concepts • Equivalence: two sentences are equivalent if they are true in same models. • Validity: a sentence is valid if it true in all models. (tautology) e. g. P or not P. – Sign: Members or not Members only. – Berra: It’s not over till its over. • Satisfiability: a sentence is satisfied if it true in some model.

Validity != Provability • Goldbach’s conjecture: Every even number (>2) is the sum of 2 primes. • This is either valid or not. • It may not be provable. • Godel: No axiomization of arithmetic will be complete, i. e. always valid statements that are not provable.

Natural Inference Rules • Modus Ponens: p, p=>q |-- q. – Sound • Resolution example (sound) – p or q, not p or r |-- q or r • Abduction (unsound, but common) – q, p=>q |-- p – ground wet, rained => ground wet |-- rained – medical diagnosis

Natural Inference Systems • Typically have dozen of rules. • Difficult for people to use. • Expensive for computation. – e. g. a |-- a or b – a and b |-- a • All known systems take exponential time in worse case. (co-np complete)

Full Propositional Resolution • • • clause 1: x 1 +x 2+. . xn+y (+ = or) clause 2: -y + z 1 + z 2 +… zm clauses contain complementary literals. x 1 +. . xn +z 1 +… zm y and not y are complementary literals. Theorem: If s 1, …sn |= s then s 1, …sn |-- s by resolution. Refutation Completeness. Factoring: (simplifying: x or x goes to x)

Conjunctive Normal Form • To apply resolution we need to write what we know as a conjunct of disjuncts. • Pg 215 contains the rules for doing this transformation. • Basically you remove all and => and move “not’s” inwards. Then you may need to apply distributive laws.

Proposition -> CNF Goal: Proving R • • • P (P&Q) =>R (S or T) => Q T Distributive laws: (-s&-t) or q (-s or q)&(-t or q). • • • P -P or –Q or R -S or Q -T or Q T Remember: implicit adding.

Resolution Proof • • • P (1) -P or –Q or R (2) -S or Q (3) -T or Q (4) T (5) ~R (6) • • • -P or –Q : 7 by 2 & 6 -Q : 8 by 7 & 1. -T : 9 by 8 & 4 empty: by 9 and 5. Done: order only effects efficiency.

Resolution Algorithm To prove s 1, s 2. . sn |-- s 1. Put s 1, s 2, . . sn & not s into cnf. 2. Resolve any 2 clauses that have complementary literals 3. If you get empty, done 4. Continue until set of clauses doesn’t grow. Search can be expensive (exponential).

Forward and Backward Reasoning • Horn clause has at most 1 positive literal. – Prolog only allows Horn clauses. – if a, b, c then d => not a or not b or not c or d – Prolog writes this: • d : - a, b, c. – Prolog thinks: to prove d, set up subgoals a, b, c and prove/verify each subgoal.

Forward Reasoning • • • From facts to conclusions Given s 1: p, s 2: q, s 3: p&q=>r Rewrite in clausal form: s 3 = (-p+-q+r) s 1 resolve with s 3 = -q+r (s 4) s 2 resolve with s 4 = r Generally used for processing sensory information.

Backwards Reasoning: what prolog does • • From Negative of Goal to data Given s 1: p, s 2: q, s 3: p&q=>r Goal: s 4 = r Rewrite in clausal form: s 3 = (-p+-q+r) Resolve s 4 with s 3 = -p +-q (s 5) Resolve s 5 with s 2 = -p (s 6) Resolve s 6 with s 1 = empty. Eureka r is true.

Davis-Putnam Algorithm • Effective, complete propositional algorithm • Basically: recursive backtracking with tricks. – early termination: short circuit evaluation – pure symbol: variable is always + or – (eliminate the containing clauses) – one literal clauses: one undefined variable, really special cases of MRV • Propositional satisfication is a special case of Constraint satisfication.

Walk. Sat • Heuristic algorithm, like min-conflicts • Randomly assign values (t/f) • For a while do – randomly select a clause – with probability p, flip a random variable in clause – else flip a variable which maximizes number of satisfied clauses. • Of course, variations exists.

Hard Satisfiability Problems • Critical point: ratio of clauses/variables = 4. 24 (empirical). • If above, problems usually unsatsifiable. • If below, problems usually satisfiable. • Theorem: Critical range is bounded by [3. 0003, 4. 598].

What can’t we say? • Quantification: every student has a father. • Relations: If X is married to Y, then Y is married to X. • Probability: There is an 80% chance of rain. • Combine Evidence: This car is better than that one because… • Uncertainty: Maybe John is playing golf.