 Пропорциональные отрезки Отрезки АВ и СD пропорциональны отрезкам А 1 В 1 и С 1 D 1, СD В 1 C если = Пример 2 1 3 1, 5 Отрезки АВ и СD пропорциональны отрезкам А 1 В 1 и С 1 D 1, =
Пропорциональные отрезки Отрезки АВ и СD пропорциональны отрезкам А 1 В 1 и С 1 D 1, СD В 1 C если = Пример 2 1 3 1, 5 Отрезки АВ и СD пропорциональны отрезкам А 1 В 1 и С 1 D 1, =
 Понятие пропорциональности вводится и для большего числа отрезков. Отрезки АВ, СD АВ СD и EF пропорциональны отрезкам А 1 В 1, С 1 D 1 и E 1 F 1, E 1 F 1 1 C 1 D 1 если = =
Понятие пропорциональности вводится и для большего числа отрезков. Отрезки АВ, СD АВ СD и EF пропорциональны отрезкам А 1 В 1, С 1 D 1 и E 1 F 1, E 1 F 1 1 C 1 D 1 если = =
 В геометрии фигуры одинаковой формы принято называть подобными.
В геометрии фигуры одинаковой формы принято называть подобными.
 Подобными являются любые два круга, два квадрата.
Подобными являются любые два круга, два квадрата.
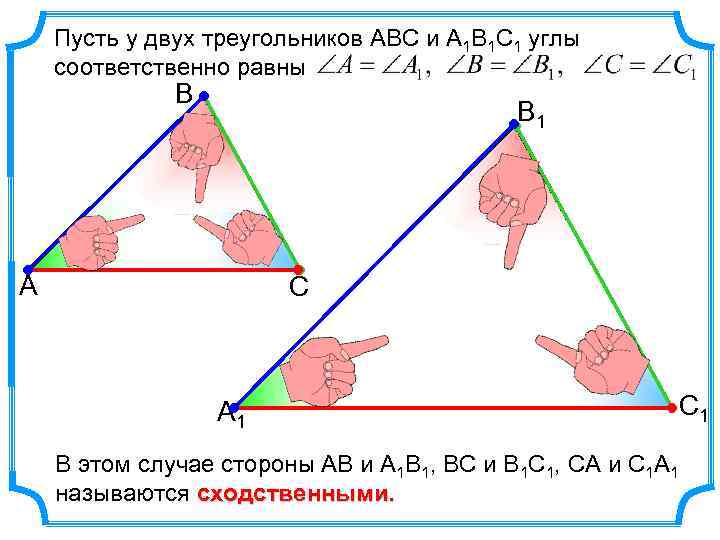 Пусть у двух треугольников АВС и А 1 В 1 С 1 углы соответственно равны В В 1 А С А 1 В этом случае стороны АВ и А 1 В 1, ВС и В 1 С 1, СА и С 1 А 1 называются сходственными. С 1
Пусть у двух треугольников АВС и А 1 В 1 С 1 углы соответственно равны В В 1 А С А 1 В этом случае стороны АВ и А 1 В 1, ВС и В 1 С 1, СА и С 1 А 1 называются сходственными. С 1
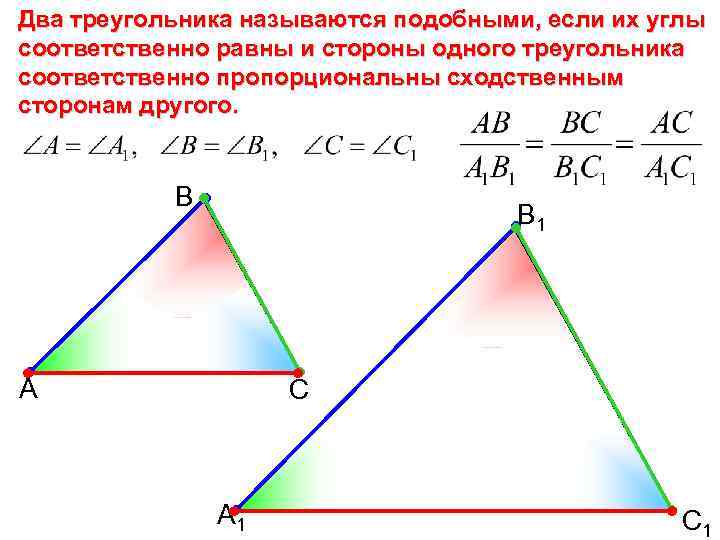 Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника соответственно пропорциональны сходственным сторонам другого. В В 1 А С А 1 С 1
Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника соответственно пропорциональны сходственным сторонам другого. В В 1 А С А 1 С 1
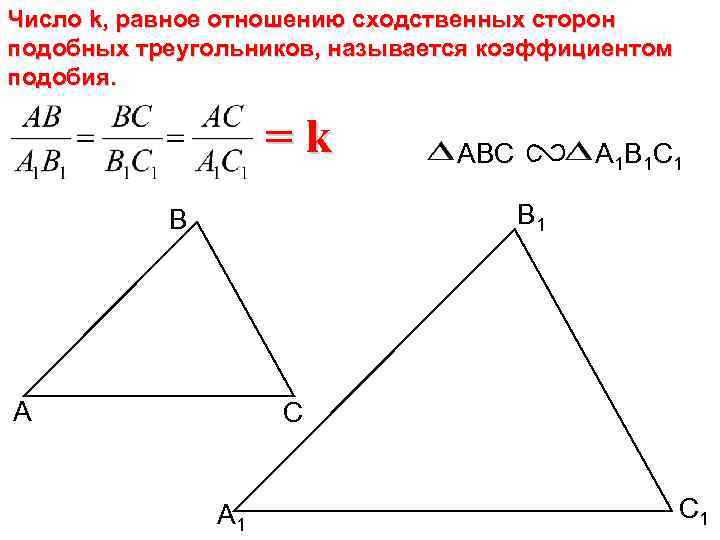 Число k, равное отношению сходственных сторон подобных треугольников, называется коэффициентом подобия. =k ABC A 1 B 1 C 1 В А С А 1 С 1
Число k, равное отношению сходственных сторон подобных треугольников, называется коэффициентом подобия. =k ABC A 1 B 1 C 1 В А С А 1 С 1
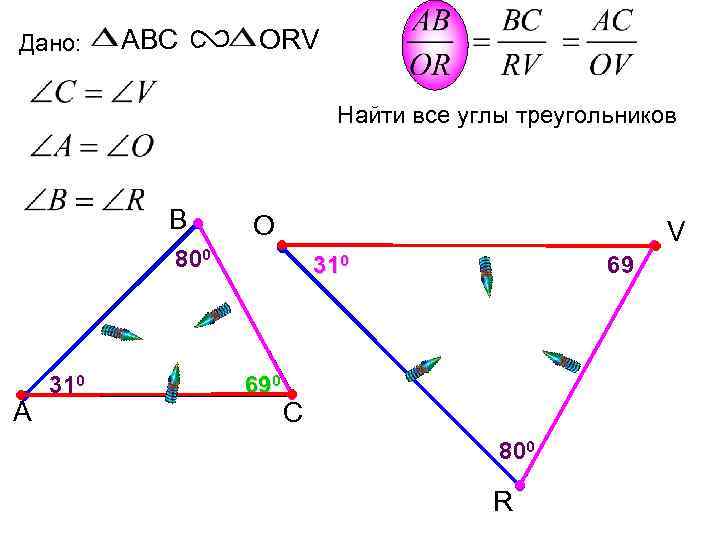 Дано: ABC ORV Найти все углы треугольников В O V 800 А 310 690 69 С 800 R
Дано: ABC ORV Найти все углы треугольников В O V 800 А 310 690 69 С 800 R
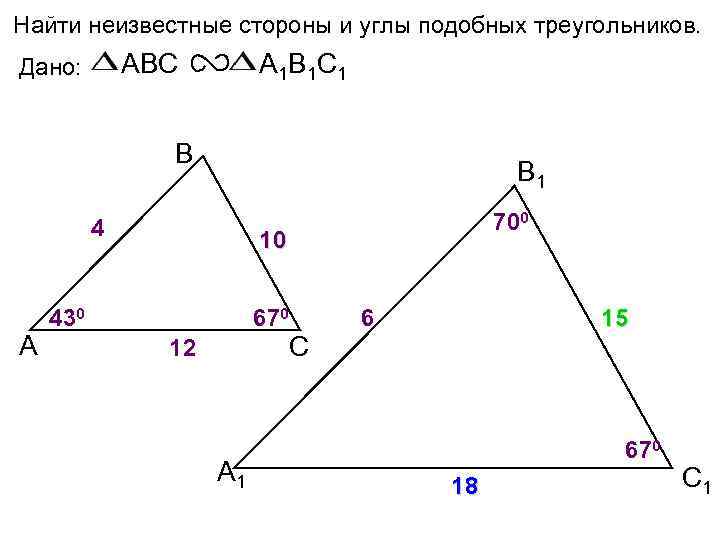 Найти неизвестные стороны и углы подобных треугольников. ABC Дано: А 1 В 1 С 1 В В 1 4 А 700 10 430 670 12 А 1 С 6 15 670 18 С 1
Найти неизвестные стороны и углы подобных треугольников. ABC Дано: А 1 В 1 С 1 В В 1 4 А 700 10 430 670 12 А 1 С 6 15 670 18 С 1
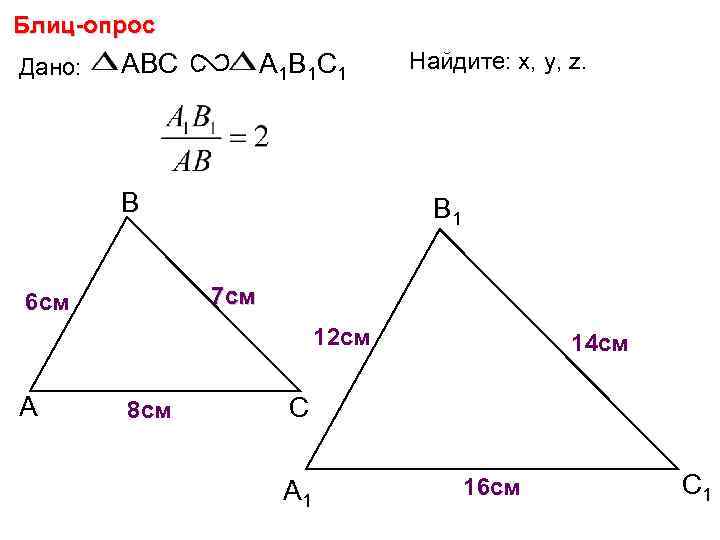 Блиц-опрос Дано: ABC А 1 В 1 С 1 В Найдите: х, у, z. В 1 7 см 6 см 12 см х А 8 см 14 см у С А 1 16 см z С 1
Блиц-опрос Дано: ABC А 1 В 1 С 1 В Найдите: х, у, z. В 1 7 см 6 см 12 см х А 8 см 14 см у С А 1 16 см z С 1
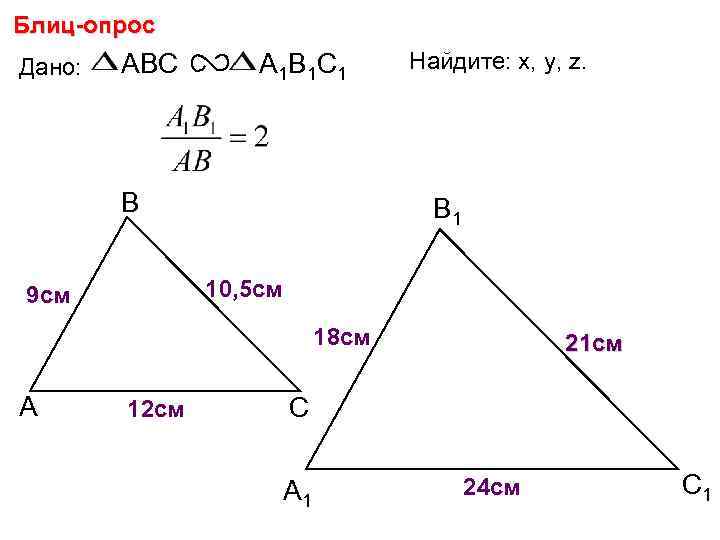 Блиц-опрос Дано: ABC А 1 В 1 С 1 В Найдите: х, у, z. В 1 10, 5 см у 9 см х 18 см А 12 см z 21 см С А 1 24 см С 1
Блиц-опрос Дано: ABC А 1 В 1 С 1 В Найдите: х, у, z. В 1 10, 5 см у 9 см х 18 см А 12 см z 21 см С А 1 24 см С 1
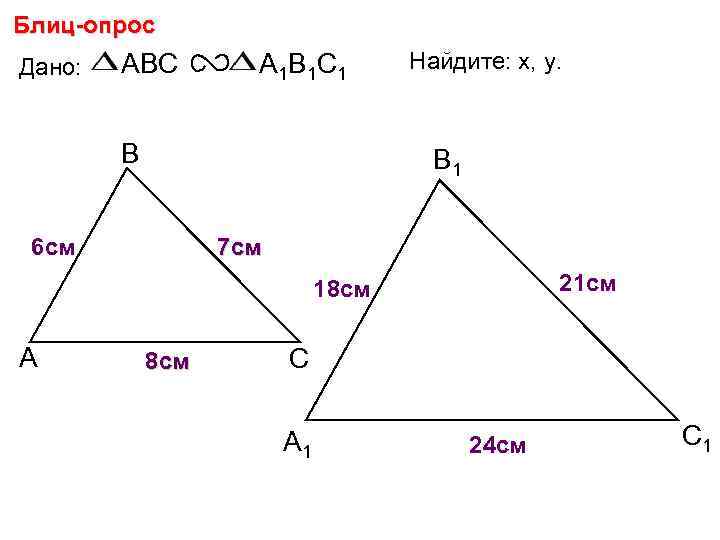 Блиц-опрос Дано: ABC А 1 В 1 С 1 В Найдите: х, у. В 1 6 см 7 см 21 см х 18 см А 8 см С А 1 у 24 см С 1
Блиц-опрос Дано: ABC А 1 В 1 С 1 В Найдите: х, у. В 1 6 см 7 см 21 см х 18 см А 8 см С А 1 у 24 см С 1
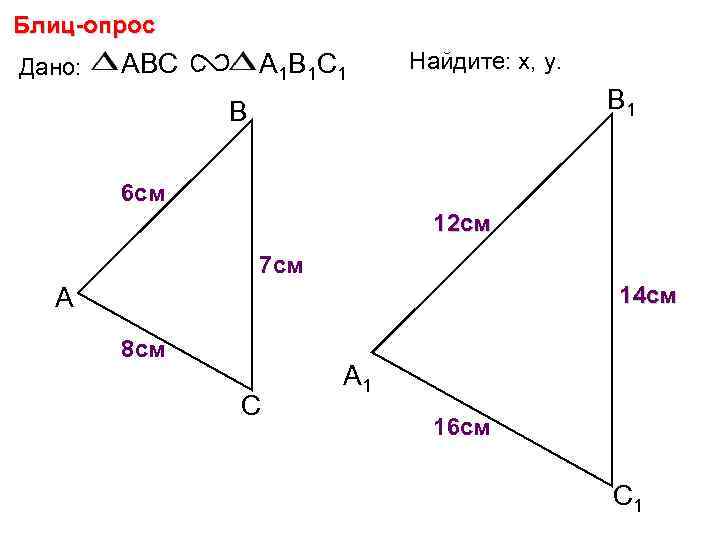 Блиц-опрос Дано: ABC А 1 В 1 С 1 Найдите: х, у. В 1 В 6 см х 12 см 7 см у 14 см А 8 см С А 1 16 см С 1
Блиц-опрос Дано: ABC А 1 В 1 С 1 Найдите: х, у. В 1 В 6 см х 12 см 7 см у 14 см А 8 см С А 1 16 см С 1
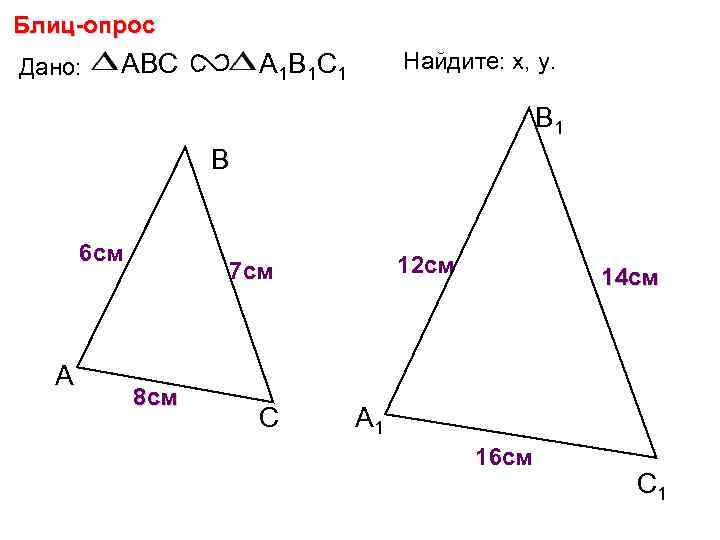 Блиц-опрос Дано: ABC Найдите: х, у. А 1 В 1 С 1 В 6 см А х 7 см 8 см С 12 см А 1 14 см у 16 см С 1
Блиц-опрос Дано: ABC Найдите: х, у. А 1 В 1 С 1 В 6 см А х 7 см 8 см С 12 см А 1 14 см у 16 см С 1
 № 547. A 1 B 1 C 1 Дано: ABC Отношение периметров двух коэффициент подобия подобных треугольников равно коэффициенту подобия. Доказать: k– +
№ 547. A 1 B 1 C 1 Дано: ABC Отношение периметров двух коэффициент подобия подобных треугольников равно коэффициенту подобия. Доказать: k– +
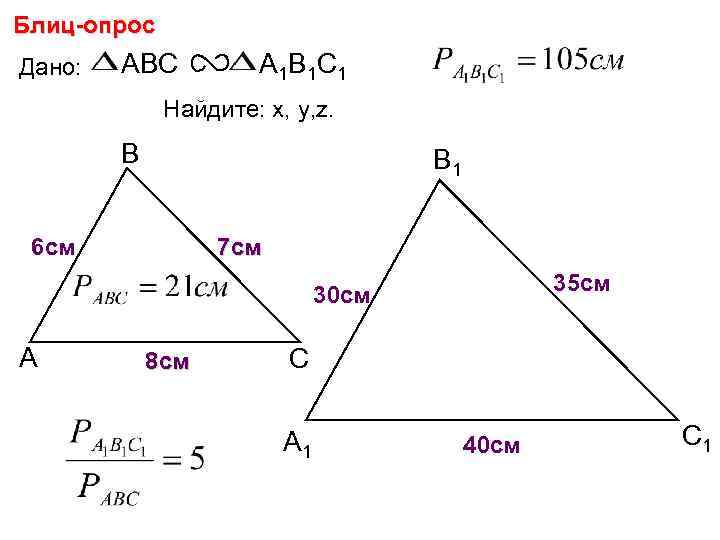 Блиц-опрос Дано: ABC А 1 В 1 С 1 Найдите: х, у, z. В В 1 6 см 7 см 35 см y х 30 см А 8 см С А 1 z 40 см С 1
Блиц-опрос Дано: ABC А 1 В 1 С 1 Найдите: х, у, z. В В 1 6 см 7 см 35 см y х 30 см А 8 см С А 1 z 40 см С 1
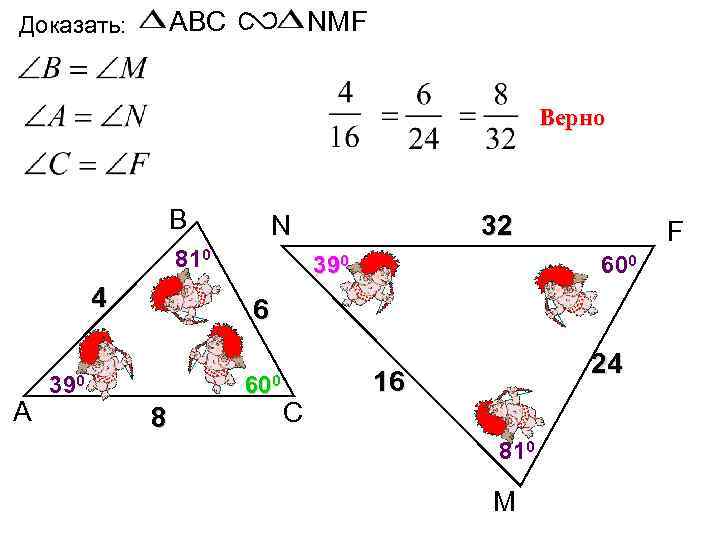 ABC Доказать: NMF Верно В N 810 4 А 32 390 F 600 6 390 600 8 С 24 16 810 М
ABC Доказать: NMF Верно В N 810 4 А 32 390 F 600 6 390 600 8 С 24 16 810 М