Properties of Kites 6 -6 Properties of Kites

Properties of Kites 6 -6 Properties of Kites and Trapezoids 6 -6 and Trapezoids Warm Up Lesson Presentation Lesson Quiz Holt Geometry

6 -6 Properties of Kites and Trapezoids Do Now Solve for x. 1. x 2 + 38 = 3 x 2 – 12 2. 137 + x = 180 3. 4. Find FE. Holt Geometry

6 -6 Properties of Kites and Trapezoids Objectives TSW use properties of kites and trapezoids to solve problems. Holt Geometry

6 -6 Properties of Kites and Trapezoids Vocabulary kite trapezoid base of a trapezoid leg of a trapezoid base angle of a trapezoid isosceles trapezoid midsegment of a trapezoid Holt Geometry

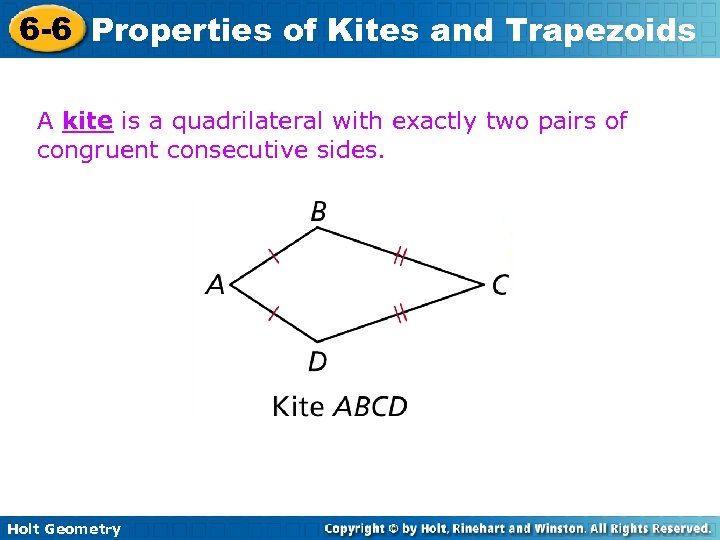6 -6 Properties of Kites and Trapezoids A kite is a quadrilateral with exactly two pairs of congruent consecutive sides. Holt Geometry

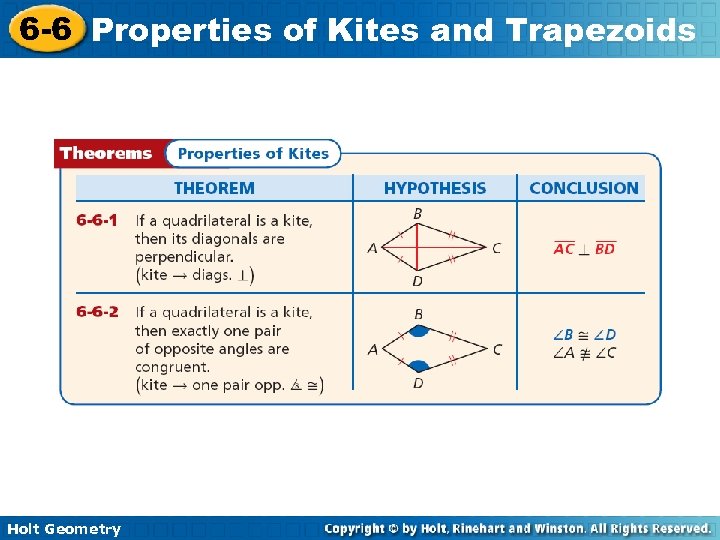6 -6 Properties of Kites and Trapezoids Holt Geometry

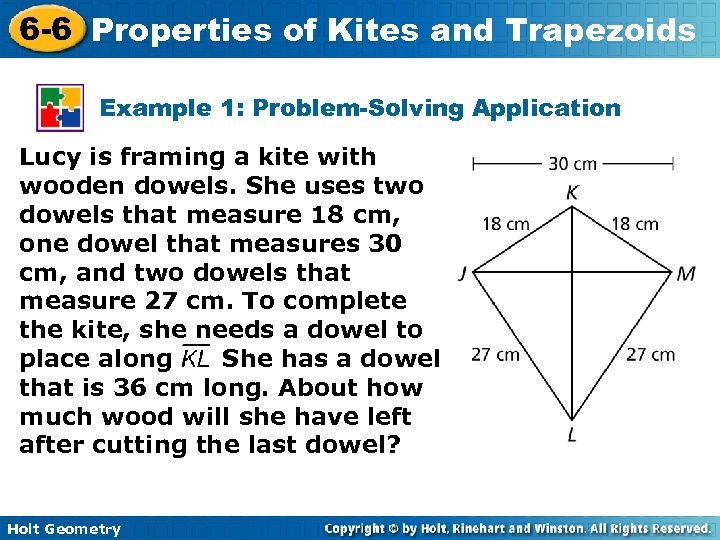6 -6 Properties of Kites and Trapezoids Example 1: Problem-Solving Application Lucy is framing a kite with wooden dowels. She uses two dowels that measure 18 cm, one dowel that measures 30 cm, and two dowels that measure 27 cm. To complete the kite, she needs a dowel to place along. She has a dowel that is 36 cm long. About how much wood will she have left after cutting the last dowel? Holt Geometry

6 -6 Properties of Kites and Trapezoids Holt Geometry

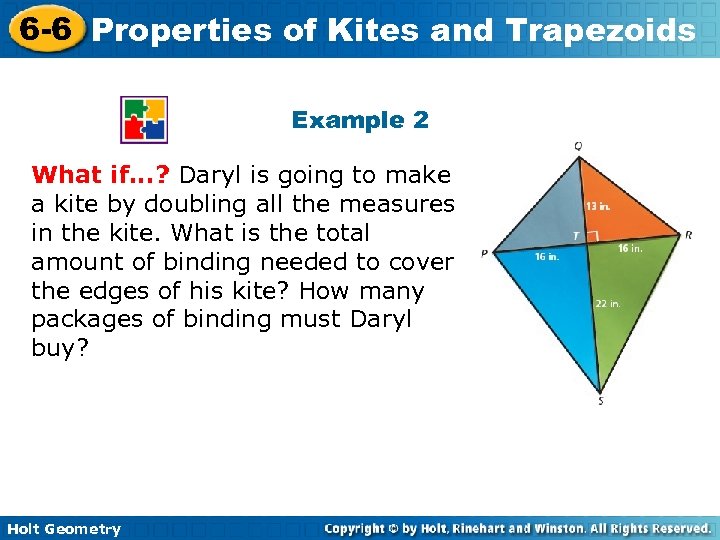6 -6 Properties of Kites and Trapezoids Example 2 What if. . . ? Daryl is going to make a kite by doubling all the measures in the kite. What is the total amount of binding needed to cover the edges of his kite? How many packages of binding must Daryl buy? Holt Geometry

6 -6 Properties of Kites and Trapezoids Holt Geometry

6 -6 Properties of Kites and Trapezoids Example 3: Using Properties of Kites In kite ABCD, m DAB = 54°, and m CDF = 52°. Find m BCD. Holt Geometry

6 -6 Properties of Kites and Trapezoids Example 3. 5: Using Properties of Kites In kite ABCD, m DAB = 54°, and m CDF = 52°. Find m ABC. Holt Geometry

6 -6 Properties of Kites and Trapezoids Example 4: Using Properties of Kites In kite ABCD, m DAB = 54°, and m CDF = 52°. Find m FDA. Holt Geometry

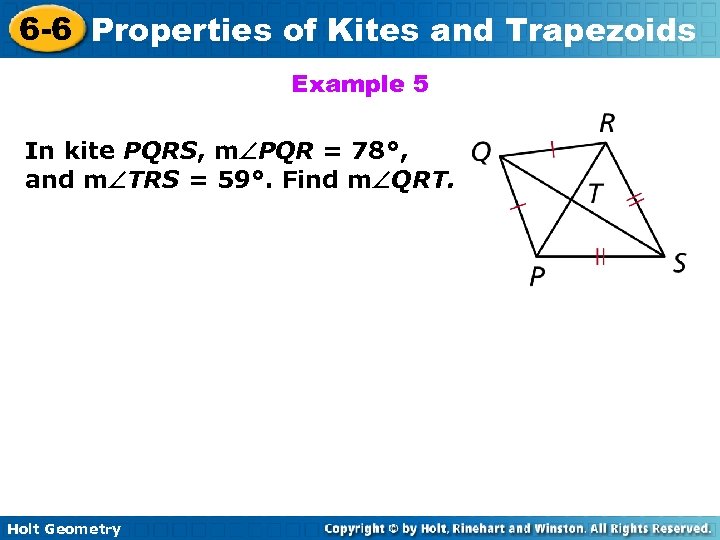6 -6 Properties of Kites and Trapezoids Example 5 In kite PQRS, m PQR = 78°, and m TRS = 59°. Find m QRT. Holt Geometry

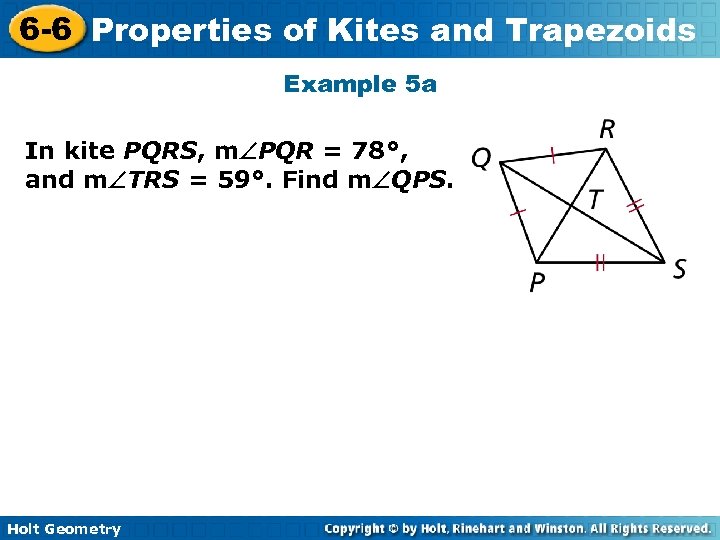6 -6 Properties of Kites and Trapezoids Example 5 a In kite PQRS, m PQR = 78°, and m TRS = 59°. Find m QPS. Holt Geometry

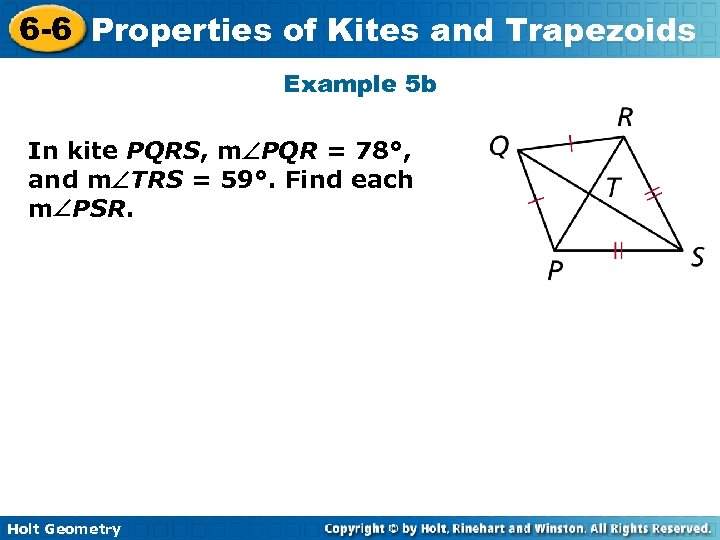6 -6 Properties of Kites and Trapezoids Example 5 b In kite PQRS, m PQR = 78°, and m TRS = 59°. Find each m PSR. Holt Geometry

6 -6 Properties of Kites and Trapezoids A trapezoid is a quadrilateral with exactly one pair of parallel sides. Each of the parallel sides is called a base. The nonparallel sides are called legs. Base angles of a trapezoid are two consecutive angles whose common side is a base. Holt Geometry

6 -6 Properties of Kites and Trapezoids If the legs of a trapezoid are congruent, the trapezoid is an isosceles trapezoid. The following theorems state the properties of an isosceles trapezoid. Holt Geometry

6 -6 Properties of Kites and Trapezoids Holt Geometry

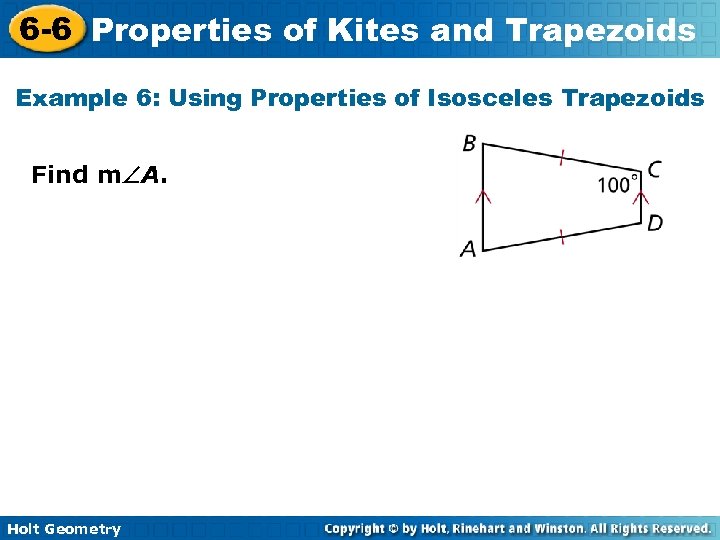6 -6 Properties of Kites and Trapezoids Example 6: Using Properties of Isosceles Trapezoids Find m A. Holt Geometry

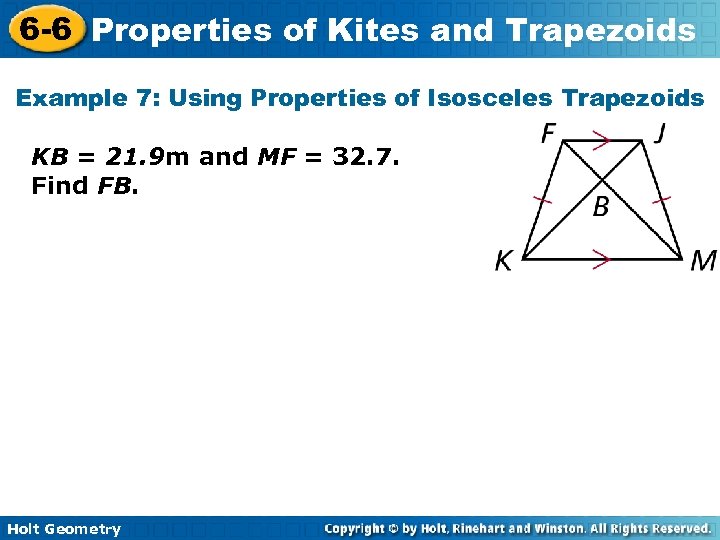6 -6 Properties of Kites and Trapezoids Example 7: Using Properties of Isosceles Trapezoids KB = 21. 9 m and MF = 32. 7. Find FB. Holt Geometry

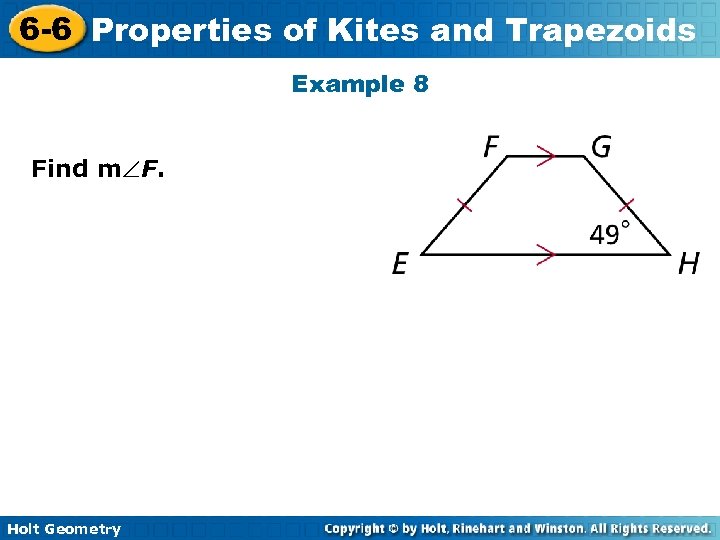6 -6 Properties of Kites and Trapezoids Example 8 Find m F. Holt Geometry

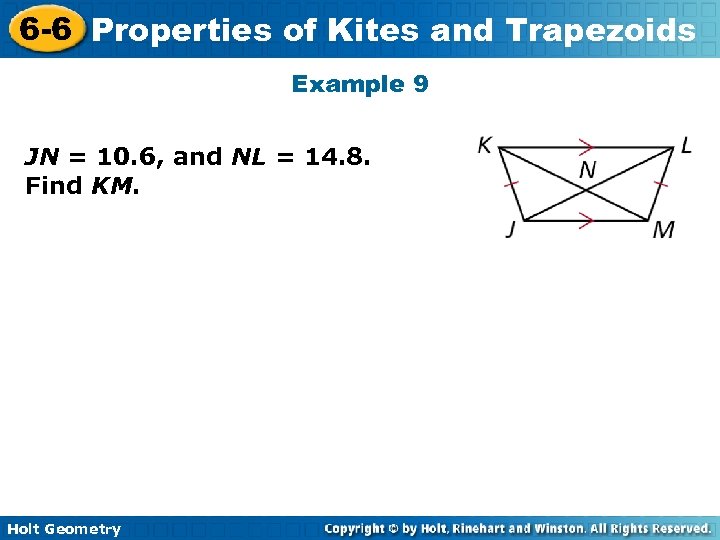6 -6 Properties of Kites and Trapezoids Example 9 JN = 10. 6, and NL = 14. 8. Find KM. Holt Geometry

6 -6 Properties of Kites and Trapezoids Example 10: Applying Conditions for Isosceles Trapezoids Find the value of a so that PQRS is isosceles. Holt Geometry

6 -6 Properties of Kites and Trapezoids Example 11: Applying Conditions for Isosceles Trapezoids AD = 12 x – 11, and BC = 9 x – 2. Find the value of x so that ABCD is isosceles. Holt Geometry

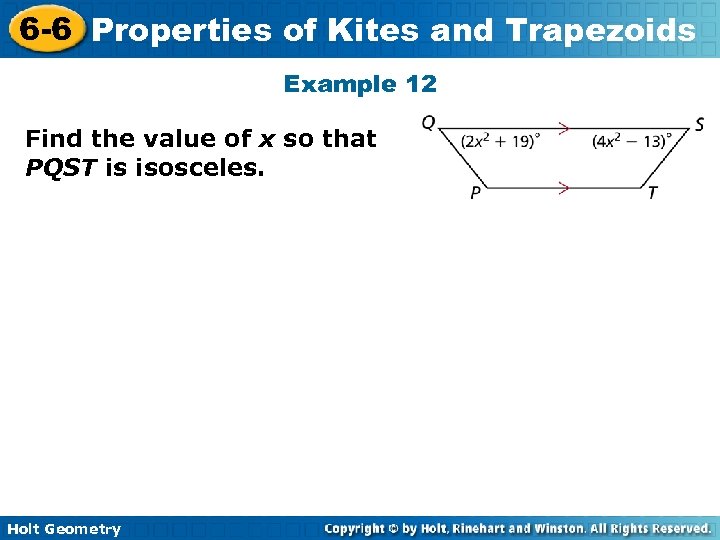6 -6 Properties of Kites and Trapezoids Example 12 Find the value of x so that PQST is isosceles. Holt Geometry

6 -6 Properties of Kites and Trapezoids The midsegment of a trapezoid is the segment whose endpoints are the midpoints of the legs. In Lesson 5 -1, you studied the Triangle Midsegment Theorem. The Trapezoid Midsegment Theorem is similar to it. Holt Geometry

6 -6 Properties of Kites and Trapezoids Holt Geometry

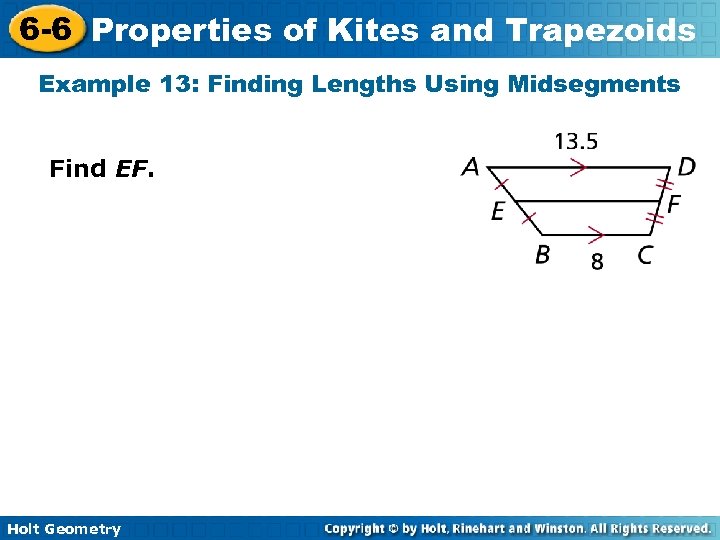6 -6 Properties of Kites and Trapezoids Example 13: Finding Lengths Using Midsegments Find EF. Holt Geometry

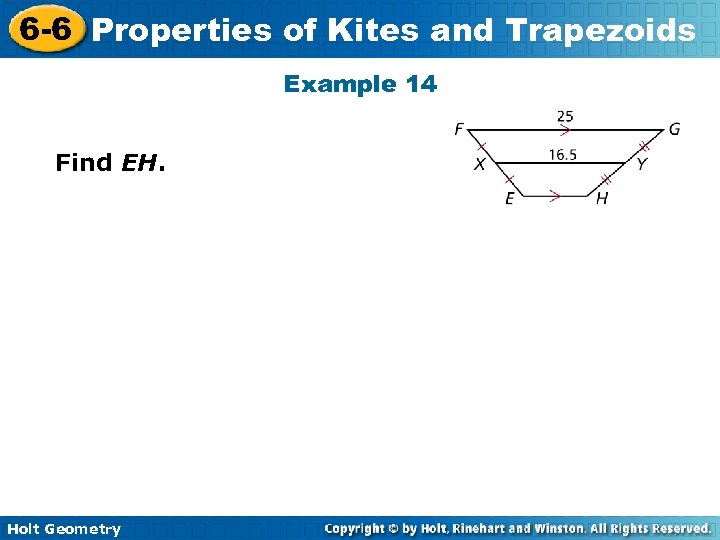6 -6 Properties of Kites and Trapezoids Example 14 Find EH. Holt Geometry

6 -6 Properties of Kites and Trapezoids Holt Geometry

6 -6 Properties of Kites and Trapezoids Lesson Quiz: Part I 1. Erin is making a kite based on the pattern below. About how much binding does Erin need to cover the edges of the kite? about 191. 2 in. In kite HJKL, m KLP = 72°, and m HJP = 49. 5°. Find each measure. 2. m LHJ Holt Geometry 81° 3. m PKL 18°

6 -6 Properties of Kites and Trapezoids Lesson Quiz: Part II Use the diagram for Items 4 and 5. 4. m WZY = 61°. Find m WXY. 119° 5. XV = 4. 6, and WY = 14. 2. Find VZ. 9. 6 6. Find LP. 18 Holt Geometry