Производные и дифференциалы функции Определение Производной функции в

Производные и дифференциалы функции Определение. Производной функции в точке называется предел Приращение аргумента Приращение функции Обозначения производной Геометрический смысл производной Производная есть тангенс угла наклона касательной к оси в точке Уравнение касательной в точке Касательная - это прямая, имеющая в окрестности точки одну общую точку с графиком функции

Механический смысл производной Производная есть мгновенная скорость изменения функции в точке Средняя скорость изменения функции Мгновенная скорость изменения функции Определение. Функция называется дифференцируемой в точке , если она имеет конечную производную в этой точке.

Основные правила дифференцирования производная от суммы, константа выносится производная от произведения производная от частного Теорема. Для того, чтобы функция была дифференцируема в точке , необходимо и достаточно выполнения равенства , где бесконечно малая более высокого порядка, чем , т. е.

Определение. Линейная часть приращения функции относительно приращения аргумента называется дифференциалом функции Формула дифференциала функции Примеры нахождения производных

Производная сложной функции Пример Производная степенно-показательного выражения Пример

Производная неявной функции Пример

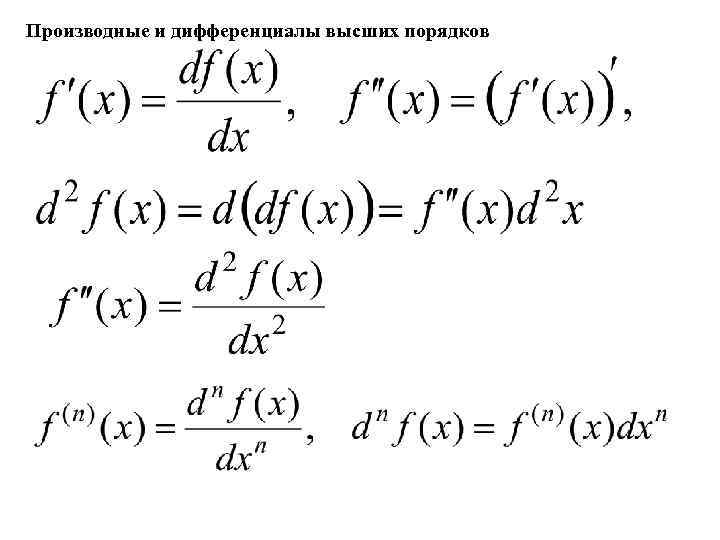Производные и дифференциалы высших порядков

Формула Тейлора Пусть функция дифференцируема в точке. Тогда её можно представить в окрестности точки в виде многочлена с остатком Формула Маклорена

Примеры рядов Маклорена

Формула Лейбница - дифференцируемые функции Формула Лейбница Пример

Правило Лопиталя Пусть функции условие Аналогично для случая дифференцируемы в точке. Тогда и выполняется

Примеры

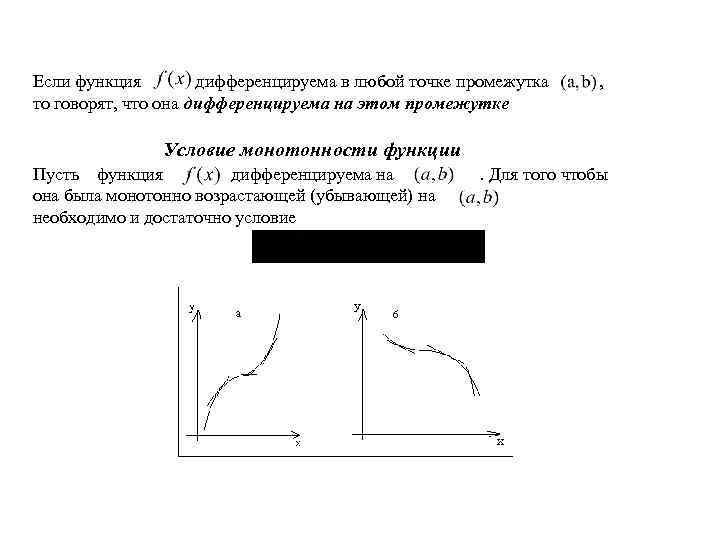Если функция дифференцируема в любой точке промежутка то говорят, что она дифференцируема на этом промежутке , Условие монотонности функции Пусть функция дифференцируема на она была монотонно возрастающей (убывающей) на необходимо и достаточно условие . Для того чтобы

Экстремумы функции Пусть определена и непрерывна на. Говорят, что функция имеет в точке максимум (локальный максимум), если в некоторой окрестности этой точки выполняется неравенство. Другими словами, точка доставляет функции максимум, если значение оказывается наибольшим значением функции в некоторой окрестности этой точки. При этом называется точкой максимума. Аналогично определяется минимум (локальный минимум). Максимумы и минимумы функции называются экстремумами. Необходимое условие экстремума Теорема Ферма. Пусть определена на и принимает в точке наибольшее или наименьшее значение. Тогда, если в точке существует конечная производная , то. • Точки, в которых , называются стационарными .

• Стационарные точки и точки, в которых производная не является конечной или не существует, являются подозрительными на экстремум Достаточные условия экстремума • Первое достаточное условие. Предположим, что функция определена в некоторой окрестности критической точки , непрерывна при и имеет всюду в рассматриваемой окрестности (кроме, быть может, самой точки ) производную. Если при переходе через критическую точку производная меняет знак, то в этой точке имеет место экстремум. В противном случае экстремума нет.

Второе достаточное условие • • Пусть функция имеет первую производную в окрестности точки вторую производную в самой точке. Предположим, что – стационарная точка, т. е. . Если вторая производная в стационарной точке больше нуля , то имеет место минимум, а если меньше нуля - максимум. Действительно, по формуле Тейлора в окрестности стационарной точки имеем. и

Выпуклость, точки перегиба • Точку • Функция имеет выпуклость вверх на данном промежутке , если ее график лежит под касательной, проведенной в любой точке рассматриваемого промежутка. Если дважды дифференцируема на , то для выпуклости вверх необходимо и достаточно выполнения условия: . • • называют точкой перегиба, если . Функция имеет выпуклость вниз на данном промежутке , если ее график лежит над касательной, проведенной в любой точке рассматриваемого промежутка. Если дважды дифференцируема на , то для выпуклости вниз необходимо и достаточно выполнения условия: . Этот факт легко усматривается из формулы Тейлора

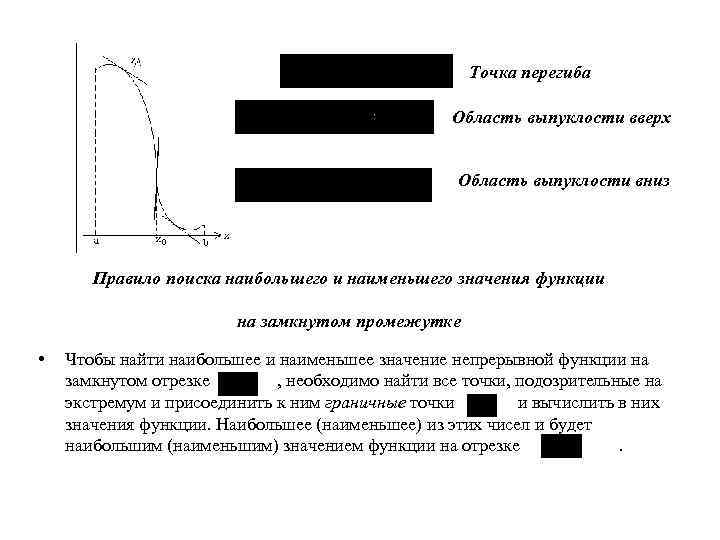Точка перегиба Область выпуклости вверх Область выпуклости вниз Правило поиска наибольшего и наименьшего значения функции на замкнутом промежутке • Чтобы найти наибольшее и наименьшее значение непрерывной функции на замкнутом отрезке , необходимо найти все точки, подозрительные на экстремум и присоединить к ним граничные точки и вычислить в них значения функции. Наибольшее (наименьшее) из этих чисел и будет наибольшим (наименьшим) значением функции на отрезке.