Производная функции может быть найдена по схеме: 1 Дадим аргументу х приращение Δх и найдем значение функции y+Δy=f(x+Δx)
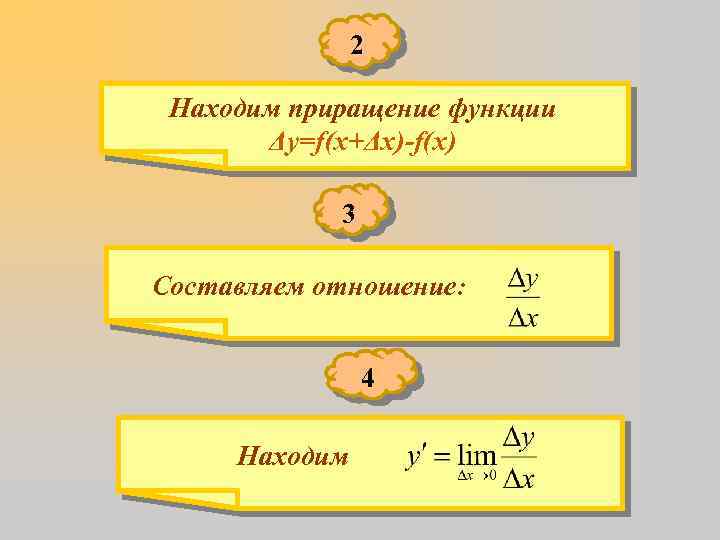
2 Находим приращение функции Δy=f(x+Δx)-f(x) 3 Составляем отношение: 4 Находим
Найдем производную функции 1 2 Дадим аргументу х приращение Δх и найдем значение функции y+Δy: Находим приращение функции
3 Составляем отношение
4 Находим Полученный результат является частным случаем производной от степенной функции Можно показать, что в общем случае
1 Производная постоянной величины равна 0: 2 Производная аргумента равна 1:
3 Производная алгебраической суммы (разности) конечного числа дифференцируемых функций равна сумме (разности) производных этих функций:
Пусть u=u(x) и v=v(x) -дифференцируемые функции. Найдем производную функции y=u + v. Дадим аргументу х приращение Δх, не равное 0, тогда функции получат значения u+Δu, v+Δv.
Находим приращение функции Составляем отношение Находим предел этого отношения:
4 Производная произведения двух дифференцируемых функций равна сумме произведений производной первого сомножителя на второй и производной второго сомножителя на первый:
Пусть u=u(x) и v=v(x) -дифференцируемые функции. Найдем производную функции y=uv. Дадим аргументу х приращение Δх, не равное 0, тогда функции получат значения u+Δu, v+Δv.
Находим приращение функции Составляем отношение
Находим предел этого отношения: Имеем по определению производной:
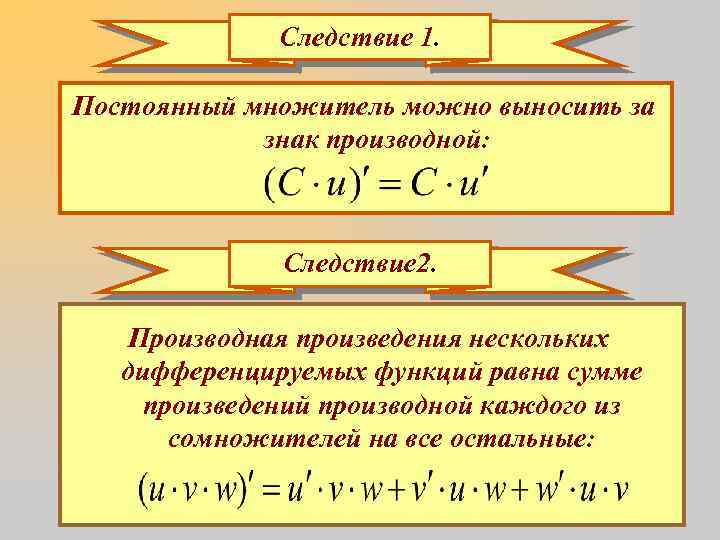
Следствие 1. Постоянный множитель можно выносить за знак производной: Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные:
5 Производная частного двух дифференцируемых функций находится по формуле:
1 Найти производную функции и вычислить ее значение в точке х=1.
Находим значение производной в точке х=1:
2 Найти производную функции и вычислить ее значение в точке х=1.
Находим значение производной в точке х=1:
3 Найти производную функции и вычислить ее значение в точке х=1.
Находим значение производной в точке х=1:
Скачать презентацию Производная функции может быть найдена по схеме 1
правила дифференцирования.ppt