Программирование на Python е Введение в информатику Глава 13

Программирование на Python’е: Введение в информатику Глава 13 Проектирование алгоритмов и рекурсия Python Programming, 2/e 1

Задачи n n n Понять базовую технику анализа эффективности алгоритмов. Знать что такое поиск и понимать алгоритмы линейного и двоичного поиска. Понимать базовые принципы рекурсивных определений и функций и уметь писать простые рекурсивные функции. Python Programming, 2/e 2

Задачи n n Понимать в деталях алгоритмы сортировки, знать алгоритмы для сортировки выбором и сортировки слиянием. Понимать как анализ алгоритмов может показать, что некоторые проблемы трудноразрешимы, а другие неразрешимы. Python Programming, 2/e 3

Поиск n n Поиск это процесс нахождения отдельного значения в множестве значений. Например, имея список членов клуба, и можно попытаться ответить на вопрос есть ли среди членов клуба люди с заданной фамилией. Для ответа на такой вопрос понадобится некая разновидность процесса поиска. Python Programming, 2/e 4

Простая проблема поиска n Ниже приводится описание простой функции поиска: def search(x, nums): # nums это список чисел, а x это число. # Возвращает позицию x в списке # или -1 если x нет в списке. n Ниже даны образцы работы функции: >>> search(4, [3, 1, 4, 2, 5]) 2 >>> search(7, [3, 1, 4, 2, 5]) -1 Python Programming, 2/e 5

Простая проблема поиска n n n В первом примере функция возвращает номер, где 4 появляется в списке. Во втором примере возвращаемое значение -1 указывает, что числа 7 нет в списке. Python включает множество встроенных методов, относящихся к поиску. Python Programming, 2/e 6

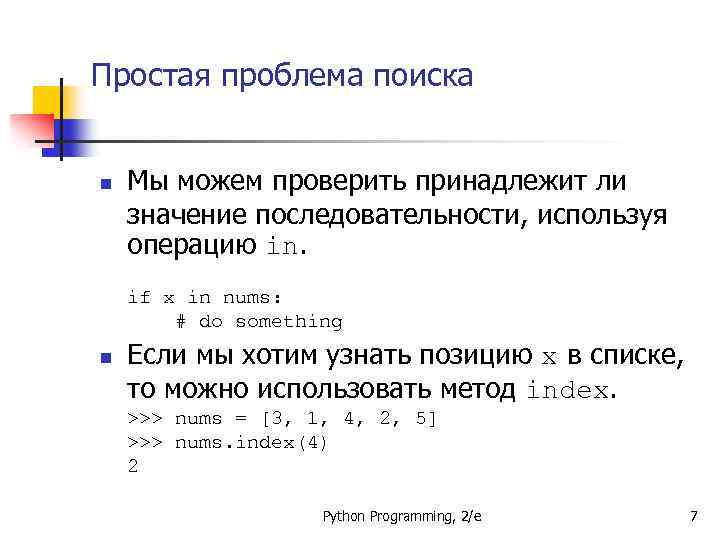Простая проблема поиска n Мы можем проверить принадлежит ли значение последовательности, используя операцию in. if x in nums: # do something n Если мы хотим узнать позицию x в списке, то можно использовать метод index. >>> nums = [3, 1, 4, 2, 5] >>> nums. index(4) 2 Python Programming, 2/e 7

Простая проблема поиска n n Единственная разница между нашей функцией search и функцией index является то, что index вызывает исключение, если целевое значение нет в списке. Мы можем реализовать функцию search, используя функцию index, просто ловя исключение и возвращая -1 для этого случая. Python Programming, 2/e 8

Простая проблема поиска n n def search(x, nums): try: return nums. index(x) except: return -1 Конечно, это будет работать, но нам действительно нужен алгоритм для поиска в списке на Python’е. Python Programming, 2/e 9

Стратегия 1: линейный поиск n n n Допустим, что вы вычислитель, и вам дали страницу случайных чисел и спросили есть ли на странице число 13. Как вы бы действовали? Вы начнёте с верха страницы, просматривая вниз, сравнивая каждое число с 13. Если вы увидите 13, то сможете сказать, что вы видели его на странице. Если просмотрите всю страницу и не увидели числа 13, то вы скажете, что его нет на странице. Python Programming, 2/e 10

Стратегия 1: линейный поиск n n n Эта стратегия называется линейным поиском, вы ищете по списку позиций, просматривая одну за одной, пока не найдёте целевое значение. def search(x, nums): for i in range(len(nums)): if nums[i] == x: # позиция найдена, возвращаем значение указателя return i return -1 # цикл закончился, позиция в списке не найдена Этот алгоритм нетрудно разработать и он неплохо работает для списков умеренных размеров. Python Programming, 2/e 11

Стратегия 1: линейный поиск n n Обе операции index в Python’е реализуют алгоритмы линейного поиска. Если набор данных достаточно большой, то имеет смысл так организовать данные, чтобы не нужно было просматривать все имеющиеся значения. Python Programming, 2/e 12

Стратегия 1: линейный поиск n n n Если данные отсортированы в возрастающем порядке (от меньших к большим), то мы можем пропустить проверку некоторых данных. Как только найдено значение, которое больше, чем целевое, то линейный поиск можно прекратить, не проверяя оставшиеся данные. В среднем, это избавит нас от половины работы. Python Programming, 2/e 13

Стратегия 2: бинарный поиск n n Если данные отсортированы, то существует стратегия поиска, которая лучше линейной, которую вы, возможно, знаете. Отгадывали ли вы когда-нибудь задуманное число от 1 до 100? Каждый раз на вашу догадку сообщается больше задуманное число, равно или меньше. Какую стратегию вы используете? Python Programming, 2/e 14

Стратегия 2: бинарный поиск n n n Маленькие дети могут просто отгадывать наобум. Дети постарше более последовательны, используя линейный поиск 1, 2, 3, 4, … пока значение не будет найдено. Большинство взрослых сначала предположат 50. Если названное значение больше, оно попадает в диапазон 51 -100. Следующим предположением будет 75. Python Programming, 2/e 15

Стратегия 2: бинарный поиск n n n Каждый раз мы называем середину оставшегося интервала чисел, стараясь еще более сузить диапазон. Эта стратегия называется бинарный (двоичный) поиск. «Би» в переводе с латыни означает два, и на каждом шаге мы делим остающуюся группу чисел на две части Python Programming, 2/e 16

Стратегия 2: бинарный поиск n n Мы можем использовать тот же подход в нашем алгоритме бинарного поиска. Мы можем использовать две переменные для отслеживания конечных точек диапазона в в отсортированном списке, в котором могут быть целевые значения. Так как цель может быть где угодно в списке, то первоначально переменная low указывает на первую позицию в списке, а переменная high на последнюю. Python Programming, 2/e 17

Стратегия 2: бинарный поиск n n n Сердцевиной алгоритма является цикл, который находит срединный элемент диапазона и сравнивает его со значением x. Если x меньше, чем срединный элемент, то high передвигается так, что поиск сужается к нижней половине диапазона. Если x больше чем срединный элемент, то low передвигается так, что поиск сужается до верхней половины диапазона. Python Programming, 2/e 18

Стратегия 2: бинарный поиск n Цикл завершается, когда n либо x найден n либо нет больше диапазона для поиска (low > high) Python Programming, 2/e 19

Стратегия 2: бинарный поиск def search(x, nums): low = 0 high = len(nums) - 1 while low <= high: mid = (low + high)//2 item = nums[mid] if x == item: return mid elif x < item: high = mid - 1 else: low = mid + 1 return -1 # Диапазон для поиска есть # Положение срединного элемента # Нашли! Возвращаем указатель # # # x в нижней половине диапазона двигаем верхний маркер вниз x iв верхней половине диапазона двигаем нижний маркер вверх не осталось диапазона для поиска x не в диапазоне Python Programming, 2/e 20

Сравнивая алгоритмы n Какой поисковый алгоритм лучше, линейный или бинарный? n n n Линейный поиск легче понять и реализовать Бинарный поиск эффективнее, так как он не требует просмотра всех элементов списка. Интуитивно можно ожидать, что линейный поиск лучше работает для маленьких списков, двоичный поиск лучше для больших списков. Но можно ли быть уверенными в этом? Python Programming, 2/e 21

Сравнивая алгоритмы n Одним из способов выполнения проверки было бы кодирование алгоритмов и их проверка на списках разных размеров с отметкой времени поиска. n n n Линейный поиск обычно быстрее для списков из 10 элементов или меньше Небольшое различие для списков из 10 -1000 элементов Бинарный поиск лучше для 1000+ (для списка из миллиона элементов бинарный поиск идёт в среднем. 0003 сек, а линейный -- 2. 5 сек) Python Programming, 2/e 22

Сравнивая алгоритмы n n Хотя данные интересны, но можем ли мы гарантировать, что эти эмпирические результаты не зависят от типа компьютера, на котором они получены, объёма памяти компьютера, быстродействия и т. д. ? Мы могли бы абстрактно рассуждать на тему эффективности алгоритмов для определения их эффективности. Можно предположить, что чем меньше «шагов» в алгоритме, тем он эффективнее. Python Programming, 2/e 23

Сравнивая алгоритмы n n Как мы считаем число «шагов» ? Компьютерные специалисты решают такие проблемы, анализируя число шагов, которые алгоритм примет по отношению к размеру или трудности конкретной проблемы, которая решается. Python Programming, 2/e 24

Сравнивая алгоритмы n n n Для поиска трудность определяется размером диапазона поиска – нужно больше шагов в диапазоне из миллиона чисел, чем из диапазона из 10 чисел. Сколько шагов нужно, чтобы найти значение в диапазоне длины n? В частности, что происходит, когда n становится очень большим? Python Programming, 2/e 25

Сравнивая алгоритмы n Давайте рассмотрим линейный поиск. n n Для списка из 10 элементов наибольшая работа, которую нужно сделать это проверить по очереди все элементы– цикл длины не большей 10. Для списка в два раза большего длина цикла будет не больше 20. Для списка в три раза большего длина цикла будет не больше 30. Требуемое количество времени связано линейно с длиной списка, n. О таких алгоритмах компьютерные специалисты говорят как об алгоритмах линейного времени. Python Programming, 2/e 26

Сравнивая алгоритмы n Теперь давайте рассмотрим бинарный поиск. n n n Допустим список состоит из 16 элементов. На каждом шаге цикла удаляется половина элементов. После первого шага остаётся 8 элементов. time through the loop, half the items are removed. After one loop, 8 items remain. После двух шагов остаётся 4 элемента. После трёх шагов остаётся 2 элемента После четырёх шагов остаётся 1 элемент. Если цикл двоичного поиска содержит i шагов, то он может найти значение в списке из 2 i Python Programming, 2/e 27 элементов.

Сравнивая алгоритмы n n Для определения того, сколько элементов было проверено в списке длины n, нам нужно решить уравнение относительно i: . Бинарный поиск пример алгоритма с log – временем – количество времени, которое нужно для решения растёт как log от размера проблемы. Python Programming, 2/e 28

Сравнивая алгоритмы n n Логарифмическое свойство может быть очень важным. Предположим, что у вас в руках телефонная книга Нью-Йорка с 12 миллионами номеров. Вы можете подойти к нью-йоркцу, упомянутому в телефонной книге, и предложить: “Я собираюсь отгадать вашу фамилию Всякий раз, когда я буду пробовать отгадать фамилию, вы скажете мне впереди или позади согласно алфавиту ваша фамилия относительно той, которую я назвал. Сколько отгадок мне понадобится? Python Programming, 2/e 29

Сравнивая алгоритмы n n Наш анализ показывает, что ответ на вопрос равен. Мы можем угадать имя нью-йоркца за 24 попытки! Для сравнения, используя линейный поиск, нам бы понадобилось в среднем 6, 000 попыток! Python Programming, 2/e 30

Сравнивая алгоритмы n Ранее мы упомянули, что Python использует линейный поиск во встроенных поисковых методах. Почему он не использует бинарный поиск? n n Бинарный поиск требует, чтобы данные были отсортированы Если данные не отсортированы, то их сначала нужно отсортировать. Python Programming, 2/e 31

Рекурсия при решении проблем n n n Основная идея алгоритма бинарного поиска – успешное деление проблемы пополам. Эта техника известна как подход «разделяй и властвуй» . «Разделяй и властвуй» делит первоначальную проблему на меньшие версии первоначальной проблемы. Python Programming, 2/e 32

Рекурсия при решении проблем n В двоичном поиске первоначальный диапазон равен всему списку. Мы находим срединный элемент… если он целевой, то поиск закончен. В противном случае мы продолжаем двоичный поиск то ли в верхней, то ли в нижней половине списка. Python Programming, 2/e 33

Рекурсия при решении проблем Алгоритм: двоичный поиск – поиск x в [nums[low]…nums[high]] mid = (low + high)//2 if low > high x is not in nums elsif x < nums[mid] выполни двоичный поиск x в [nums[low]…nums[mid-1]] else выполни двоичный поиск x in [nums[mid+1]…nums[high]] n В этой версии нет цикла и кажется, что она ссылается сама на себя! Что происходит? ? Python Programming, 2/e 34

Рекурсивные определения n n Описание чего-либо, что ссылается на себя называется рекурсивным определением. В последнем примере алгоритм двоичного поиска использует своё собственное описание “вызов” бинарного поиска (“recurs” обращение к себе) внутри определения – отсюда название “рекурсивное определение. ” Python Programming, 2/e 35

Рекурсивные определения n n n Слышали ли вы ранее от своих учителей, что нельзя использовать определение в самом определении? Для таких определений придумано специальное название круговое определение. Рекурсия часто используется в математике Наиболее часто встречающийся пример – факториал: Например, 5! = 5(4)(3)(2)(1), или 5! = 5(4!) Python Programming, 2/e 36

Рекурсивные определения n Другими словами, n Или n Это определение говорит, что 0! равно 1, а факториал любого натурального числа равен числу, умноженному на факториал меньшего числа. Python Programming, 2/e 37

Рекурсивные определения n Наше определение рекурсивно, но оно не круговое. Рассмотрим 4! n 4! = 4(4 -1)! = 4(3!) n Что такое 3!? Мы снова применяем определение 4! = 4(3!) = 4[3(3 -1)!] = 4(3)(2!) n И так далее… 4! = 4(3!) = 4(3)(2)(1!) = 4(3)(2)(1)(0!) = 4(3)(2)(1)(1) = 24 Python Programming, 2/e 38

Рекурсивные определения n n Определение факториала не круговое, потому что мы в конце концов доходим до числа 0!, которое просто равно 1. Этот случай называется базовым случаем рекурсии. Когда базовый случай встречен, мы получаем замкнутое выражение, которое может быть вычислено. Python Programming, 2/e 39

Рекурсивные определения n Все хорошие рекурсивные определения имеют две ключевые характеристики: n n n Существует один или более базовых случаев, к которым рекурсия не применяется. Все цепи рекурсий в конце концов заканчиваются базовыми случаями. Простейший способ осуществиться двум условиям заключается в том, что каждая рекурсия упрощает первоначальную проблему. Очень маленькая версия первоначальной проблемы, которую можно решить не прибегая к рекурсии, становится базовым случаем. Python Programming, 2/e 40

Рекурсивные функции n n Мы уже знаем, что факториал можно вычислить, используя цикл с накопителем. Приведённое выше определение факториала можно записать в виде отдельной функции: def fact(n): if n == 0: return 1 else: return n * fact(n-1) Python Programming, 2/e 41

Рекурсивные функции n n Мы написали определение функции, которая вызывает сама себя, рекурсивной функции. Функция сначала проверяет не базовый ли у нас случай (n==0). Если да, то возвращает 1. В противном случае возвращает результат умножения n на факториал от (n-1), fact(n-1). Python Programming, 2/e 42

Рекурсивные функции >>> fact(4) 24 >>> fact(10) 3628800 >>> fact(100) 9332621544394415268169923885626670049071596826438 16214685929638952175999932299156089414639761565 1828625369792082722375825118521091686400000000 L >>> n Вспомните, что каждый вызов функции начинает эту функцию заново, со своими копиями локальных переменных и параметров. Python Programming, 2/e 43

Рекурсивные функции Python Programming, 2/e 44

Пример: обращение цепочки n n У Python’овских списков есть встроенные методы, которые можно использовать, чтобы обратить списки. А что если вы хотите обратить цепочку Если вы захотите сделать это сами, то один из способов будет заключаться в том, чтобы перевести цепочку в список символов, обратить список и преобразовать список назад в цепочку символов. Python Programming, 2/e 45

Пример: обращение цепочки n n С помощью рекурсии можно вычислить обратную цепочку без промежуточного «списочного» шага. Думайте о цепочке как о рекурсивном объекте: n n Разделите её на первый символ и «всё остальное» Обратите «остальное» и добавьте первый символ в конец обращенного «остального» Python Programming, 2/e 46

Пример: обращение цепочки n n n def reverse(s): return reverse(s[1: ]) + s[0] Срез s[1: ] возвращает всё кроме первого символа цепочки. Мы обращаем срез и затем добавляем с помощью конкатенации первый символ (s[0]) в конец обращенного среза. Python Programming, 2/e 47

", line" src="https://present5.com/presentation/82955572_143873530/image-48.jpg" alt="Пример: обращение цепочки n >>> reverse("Hello") Traceback (most recent call last): File "", line" /> Пример: обращение цепочки n >>> reverse("Hello") Traceback (most recent call last): File "", line 1, in -toplevelreverse("Hello") File "C: /Program Files/Python 2. 3. 3/z. py", line 8, in reverse return reverse(s[1: ]) + s[0] … File "C: /Program Files/Python 2. 3. 3/z. py", line 8, in reverse return reverse(s[1: ]) + s[0] Runtime. Error: maximum recursion depth exceeded n Что случилось? Было 1000 строк ошибок! Python Programming, 2/e 48

Пример: обращение цепочки n n Запомните: чтобы построить корректную рекурсивную функцию, нужно определить базовые случаи, к которым рекурсия неприменима. Мы забыли включить базовый случай, поэтому наша программа это бесконечная рекурсия. Каждый вызов reverse содержит другой вызов reverse, поэтому ни один из вызовов не заканчивает работу. Python Programming, 2/e 49

Пример: обращение цепочки n n n Всякий вызов функции требует определённый объём памяти. Python останавливается после 1000 вызовов, 1000 это значение по умолчанию «максимальной рекурсивной глубины» . Что следует нам использовать в качестве базового случая? Следуя нашему алгоритму, мы знаем, что в конце концов нам нужно будет обратить пустую цепочку. Так как пустая строка равна своей обратной, то её можно использовать в качестве базового случая. Python Programming, 2/e 50

Пример: обращение цепочки n n def reverse(s): if s == "": return s else: return reverse(s[1: ]) + s[0] >>> reverse("Hello") 'olle. H' Python Programming, 2/e 51

Пример: анаграммы n n Анаграмма формируется перестановкой букв слова. Формирование анаграммы это специальный случай порождения всех перестановок последовательности, проблема, которая часто встречается в математике и информатике. Python Programming, 2/e 52

Пример: анаграммы n Давайте применим тот же подход, что и в предыдущем примере. n Вырежем первый символ из цепочки. n Поместим первый символ во все возможные положения в анаграммах, сформированных из «остатка» первоначальной цепочки. Python Programming, 2/e 53

Пример: анаграммы n n n Предположим, что первоначальная цепочка равна “abc”. Удаление из неё “a” оставляет нам “bc”. Порождение всех анаграмм из “bc” даёт нам “bc” и “cb”. Чтобы сформировать анаграмму первоначальной строки, мы помещаем “a” во все возможные положения в двух меньших анаграммах: [“abc”, “bac”, “bca”, “acb”, “cab”, “cba”] Python Programming, 2/e 54

Пример: анаграммы n n Как и в предыдущем примере, мы можем использовать пустую строку в качестве базового случая. def anagrams(s): if s == "": return [s] else: ans = [] for w in anagrams(s[1: ]): for pos in range(len(w)+1): ans. append(w[: pos]+s[0]+w[pos: ] ) return ans Python Programming, 2/e 55

Пример: анаграммы n n Для накопления результатов используем список. Внешний цикл for пробегает все анаграммы, составленные из хвоста s. Внутренний цикл проставляет первый символ на все позиции в анаграмме и тем самым создаёт новую цепочку. Внутренний цикл доходит до позиции len(w)+1, поэтому первый символ может быть добавлен в конец анаграммы. Python Programming, 2/e 56

Пример: анаграммы n w[: pos]+s[0]+w[pos: ] n n n w[: pos] задаёт часть w до, но не включая символ с номером pos. w[pos: ] задаёт всё с символа с номером pos до конца цепочки. Вставка s[0] между ними означает вставку s[0] на позицию pos в цепочке w. Python Programming, 2/e 57

Пример: анаграммы n n Число анаграмм слова равно факториалу длины слова. >>> anagrams("abc") ['abc', 'bac', 'bca', 'acb', 'cab', 'cba'] Python Programming, 2/e 58

Пример: быстрое возведение в степень n n Одним из способов вычислить an для целого n заключается в умножении a на себя n раз. Это можно сделать с помощью простого цикла: def loop. Power(a, n): ans = 1 for i in range(n): ans = ans * a return ans Python Programming, 2/e 59

Пример: быстрое возведение в степень n n n Мы можем также решить эту проблему методом «разделяй и властвуй» . Из закона сложения показателей, 28 = 24(24). Если мы знаем 24, мы можем вычислить 28 используя одно умножение. Чему равно 24? 24 = 22(22), и 22 = 2(2) = 4, 4(4) = 16, 16(16) = 256 = 28 Мы вычислили 28 с помощью всего лишь трёх умножений! Python Programming, 2/e 60

Пример: быстрое возведение в степень n n n Можно воспользоваться тем, что an = an//2(an//2) Это работает только для четных n. А если n нечетное? 29 = 24(24)(21) Python Programming, 2/e 61

Пример: быстрое возведение в степень n n n Этот метод полагается на целочисленное деление (если n =9, тогда n//2 = 4). Чтобы выразить алгоритм рекурсивно, нам нужны подходящие базовые случаи. Если мы будем постоянно уменьшать значение n, n в конце концов станет равным 0 (1//2 = 0), а a 0 = 1 для любого значения, исключая a = 0. Python Programming, 2/e 62

Пример: быстрое возведение в степень n n def rec. Power(a, n): # возводит a в целую степень n if n == 0: return 1 else: factor = rec. Power(a, n//2) if n%2 == 0: # n четно return factor * factor else: # n нечетно return factor * a Здесь введена временная переменная factor , поэтому нам не нужно дважды вычислять an//2. Python Programming, 2/e 63

Пример: двоичный поиск n n n После того, как мы разобрали несколько примеров рекурсии, мы готовы выполнить бинарный поиск рекурсивно. Вспомните: мы рассматриваем сначала срединное значение, затем то ли верхнюю, то ли нижнюю половину списка. Базовые случаи получаются тогда, когда мы можем закончить поиск или нам просто негде искать. Python Programming, 2/e 64

Пример: двоичный поиск n n Рекурсивный вызов обрежет диапазон поиска наполовину всякий раз, когда у нас есть неисследованный диапазон значений, который может содержать целевое значение. Каждый вызов поисковой подпрограммы проводит поиск в списке, ограниченном нижним low и верхним high параметрамиуказателями. Python Programming, 2/e 65

Пример: двоичный поиск n n def rec. Bin. Search(x, nums, low, if low > high: # return -1 mid = (low + high)//2 item = nums[mid] if item == x: return mid elif x < item: # return rec. Bin. Search(x, else: # return rec. Bin. Search(x, high): негде искать, возвращаем -1 Смотрим нижнюю половину nums, low, mid-1) Смотрим верхнюю половину nums, mid+1, high) После этого мы можем вызвать бинарный поиск с общей search wrapping функцией: def search(x, nums): return rec. Bin. Search(x, nums, 0, len(nums)-1) Python Programming, 2/e 66

Рекурсия vs. итерация n n n Существуют сходства между итерациями (циклом) и рекурсией. Действительно, всё, что делается в цикле, можно сделать с помощью простой рекурсивной функции. Некоторые языки программирования используют исключительно рекурсию. Некоторые проблемы, которые легко решить с помощью рекурсии трудно решаемы с помощью циклов. Python Programming, 2/e 67

Рекурсия vs. итерация n n При вычислении факториала и бинарном поиске циклические и рекурсивные решения используют одинаковые алгоритмы, поэтому и их эффективность приблизительно одинакова. В решении проблемы возведения в степень используются разные алгоритмы. Циклическая версия требует линейное время для завершения работы. Рекурсивная версия выполняется за , while log-время. Разница та же, что и разница между линейным и бинарным поиском. Python Programming, 2/e 68

Рекурсия vs. итерация n n Итак… будут ли рекурсивные решения всегда настолько же эффективны или более эффективны, чем их итерационные аналоги? Последовательность Фибоначчи это последовательность чисел 1, 1, 2, 3, 5, 8, … n Последовательность начинается с двух 1. n Дальнейшие числа вычисляются как суммы двух предыдущих. Python Programming, 2/e 69

Рекурсия vs. итерация n Циклическая версия: n n n Будем использовать две переменные, curr и prev, чтобы вычислить следующее значение последовательности. После вычисления полагаем prev равным curr, и curr равным только что вычисленному числу. Всё что нужно это написать предыдущее предложение в теле цикла и выполнить цикл нужное количество раз. Python Programming, 2/e 70

Рекурсия vs. итерация n def loopfib(n): # возвращает n-ое число Фибоначчи curr = 1 prev = 1 for i in range(n-2): curr, prev = curr+prev, curr return curr n n Отметим одновременное присваивание для вычисления новых значений переменных curr и prev. Цикл выполняется только (n-2 ) раз, так как первые два значения “определены”. Python Programming, 2/e 71

Рекурсия vs. итерация n n n У последовательности Фибоначчи есть и рекурсивное определение: Рекурсивное определение можно прямо преобразовать в рекурсивную функцию. def fib(n): if n < 3: return 1 else: return fib(n-1)+fib(n-2) Python Programming, 2/e 72

Рекурсия vs. итерация n n Функция подчиняется законам, которые мы установили. n Рекурсия всегда основана на меньших значениях. n Существуют нерекурсивные базовые случаи. Итак, эта функция будет работать, не так ли? – как будто… Python Programming, 2/e 73

Рекурсия vs. итерация n Рекурсивное решение очень неэффективно, потому что оно осуществляет повторные вычисления Python Programming, 2/e 74

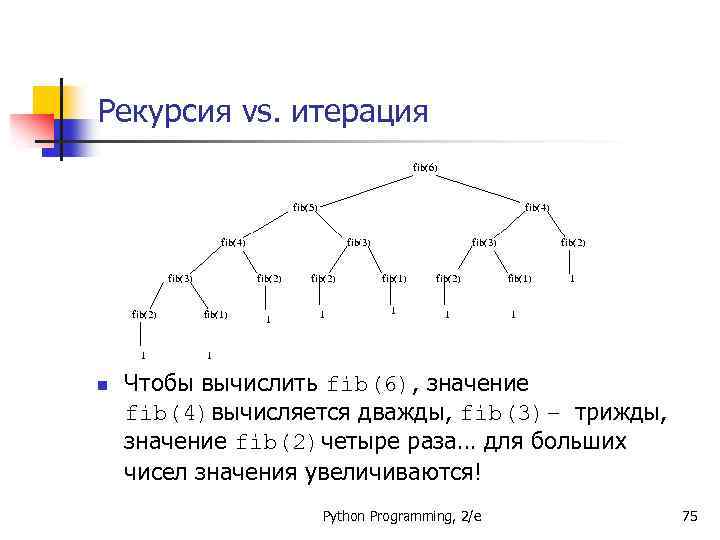Рекурсия vs. итерация n Чтобы вычислить fib(6), значение fib(4)вычисляется дважды, fib(3)– трижды, значение fib(2)четыре раза… для больших чисел значения увеличиваются! Python Programming, 2/e 75

Рекурсия vs. итерация n n Рекурсия еще одно средство в вашем арсенале способов решений проблем. Иногда рекурсия даёт более элегантное и эффективное решение, чем циклическая версия. В других случаях, когда алгоритмы похожи, преимущество переходит к циклической версии решения Избегайте рекурсивных решений, если они неэффективны, исключая случаи, когда не удаётся найти итеративное решение (что иногда случается). Python Programming, 2/e 76

Алгоритмы сортировки n Основная проблема сортировки заключается в том, чтобы взять список и переставить его элементы так, чтобы они были расположены в возрастающем (или убывающем) порядке. Python Programming, 2/e 77

Наивная сортировка: выборочная сортировка n Чтобы начать, пусть вам дали груду перемешанных картотечных карточек, на каждой из которых есть порядковый номер. Как вы заново упорядочите карточки? Python Programming, 2/e 78

Наивная сортировка: выборочная сортировка n n n Один простой метод заключается в том, чтобы просмотреть всю груду, найти карточку с наименьшим номером и поставить её на первое место. Затем просмотреть еще раз, найти следующее наименьшее значение среди оставшихся карточек, и поставить её на второе место. Намылить, прополаскать, повторить, пока карточки не будут упорядочены. Python Programming, 2/e 79

Наивная сортировка: выборочная сортировка n n У нас уже есть алгоритм для нахождения наименьшего элемента в списке (Глава 7). Когда вы идёте по списку, отслеживайте наименьший элемент, виденный до текущего момента, актуализируя его, когда найден меньший элемент. Этот сортировочный алгоритм называется сортировкой выбором. Python Programming, 2/e 80

Наивная сортировка: выборочная сортировка n Алгоритм содержит цикл и каждый раз после прохождения тела цикла наименьший оставшийся элемент выбирается и ставится на правильное место. n n Для n элементов, мы находим наименьшее значение и ставим на 0 -ю позицию. Затем мы находим наименьшее оставшееся значение среди элементов, занимающих позиции от 1 до (n-1), и ставим его в позицию 1. Элемент с наименьшим значением из позиций 2 … (n-1) переставляем во вторую позицию. И т. д. Python Programming, 2/e 81

Наивная сортировка: выборочная сортировка n n n Когда мы помещаем элемент на правильную позицию, нам нужно быть уверенными, что мы не потеряем случайно элемент, бывший на той позиции. Если элемент с наименьшим значением в позиции 10, перемещение его в позицию 0 включает присвоение: nums[0] = nums[10] Присвоение уничтожает первоначальное значение в nums[0]! Python Programming, 2/e 82

Наивная сортировка: выборочная сортировка n n Мы можем использовать одновременное присваивание, чтобы поменять местами nums[0] и nums[10]: nums[0], nums[10] = nums[10], nums[0] Используя эти идеи, мы можем реализовать наш алгоритм, используя bottom для заполненной в данный момент позиции и mp позиция элемента с наименьшим остающимся значением. Python Programming, 2/e 83

Наивная сортировка: выборочная сортировка def sel. Sort(nums): # сортируем список nums в возрастающем порядке n = len(nums) # Для каждой позиции в списке (исключая самую последнюю) for bottom in range(n-1): # находим наименьший элемент в nums[bottom]. . nums[n-1] mp = bottom # bottom первоначально наименьший for i in range(bottom+1, n): # ищем в каждой позиции if nums[i] < nums[mp]: # этот меньше mp = i # запоминаем индекс # swap smallest item to the bottom nums[bottom], nums[mp] = nums[mp], nums[bottom] Python Programming, 2/e 84

Наивная сортировка: выборочная сортировка n n n Вместо запоминания минимального значения, встреченного до сих пор, мы запоминаем его положение в списке в переменную mp. Новые значения проверяются сравнением элемента в позиции i с элементом в позиции mp. bottom попадает в диапазон от второго до последнего элемента списка. Почему? Если все элементы вплоть до последнего упорядочены, то последний элемент должен быть наибольшим. Python Programming, 2/e 85

Наивная сортировка: выборочная сортировка n Сортировку выбором легко написать. Она хорошо работает в случае списков умеренного размера, но она не очень эффективна. Мы немного проанализируем этот алгоритм. Python Programming, 2/e 86

Разделяй и властвуй: сортировка слиянием n n Мы видели как подход «разделяй и властвуй» работает в случае других проблем. А как его применить к сортировке? Пусть у вас и вашего друга есть перемешанная колода карт, которую вы хотели бы отсортировать. Каждый из вас мог бы взять половину карт и отсортировать их. Тогда всё что нужно это способ воссоединить две отсортированные части в одну колоду. Python Programming, 2/e 87

Разделяй и властвуй: сортировка слиянием n n Процесс воссоединения называется слиянием. Наш алгоритм сортировки слиянием выглядит так: разбиваем nums на две половины сортируем первую половину сортируем вторую половину сливаем две отсортированные половины назад в nums Python Programming, 2/e 88

Разделяй и властвуй: сортировка слиянием n Шаг 1: разбиваем nums на две половины n n Просто! Достаточно воспользоваться обрезанием! Шаг 4: сливаем две отсортированные половины назад в nums n n Это просто, если бы вы подумали как это сделать самому … У вас есть две отсортированные кучи, каждая с наименьшим значением сверху. То, которое меньше, будет первым элементом списка. Python Programming, 2/e 89

Разделяй и властвуй: сортировка слиянием n n n Когда наименьшее значение удалено, сравниваем две верхние карты. Та, которая меньше, будет второй в списке. Продолжаем процесс помещения наименьшей из двух верхних карт в список, пока одна из куч не будет исчерпана. В этом случае список заканчивается оставшейся кучей карт. В следующем коде lst 1 и lst 2 меньшие списки, а lst 3 больший список для результата слияния. Длина lst 3 должна быть равна сумме длин списков lst 1 и lst 2. Python Programming, 2/e 90

Разделяй и властвуй: сортировка слиянием def merge(lst 1, lst 2, lst 3): # сливаем отсортированные списки lst 1 и lst 2 в lst 3 # эти указатели отслеживают текущее положение в каждом списке i 1, i 2, i 3 = 0, 0, 0 # все начинаются с начала n 1, n 2 = len(lst 1), len(lst 2) # цикл пока в обоих списках while i 1 < n 1 and i 2 < n 2: if lst 1[i 1] < lst 2[i 2]: lst 3[i 3] = lst 1[i 1] i 1 = i 1 + 1 else: lst 3[i 3] = lst 2[i 2] i 2 = i 2 + 1 i 3 = i 3 + 1 lst 1 и lst 2 есть элементы # верхний из lst 1 меньше # копируем его в текущую позицию lst 3 # верхний из lst 2 меньше # копируем его в текущую позицию lst 3 # элемент добавлен к lst 3, # актуализируем позицию Python Programming, 2/e 91

Разделяй и властвуй: сортировка слиянием # Теперь то ли lst 1 то ли lst 2 пуст. Один из следующих циклов # завершит слияние. # Копируем оставшиеся элементы из lst 1 while i 1 < n 1: lst 3[i 3] = lst 1[i 1] i 1 = i 1 + 1 i 3 = i 3 + 1 # Копируем оставшиеся элементы из lst 2 while i 2 < n 2: lst 3[i 3] = lst 2[i 2] i 2 = i 2 + 1 i 3 = i 3 + 1 Python Programming, 2/e 92

Разделяй и властвуй: сортировка слиянием n n Мы можем разрезать список на две части, и мы можем объединить отсортированные списки в один список. Как мы собираемся сортировать меньшие списки? Мы пытаемся отсортировать список, и алгоритм требует два меньших отсортированных списка… это звучит как работа для рекурсии. Python Programming, 2/e 93

Разделяй и властвуй: сортировка слиянием n n Нам нужно найти хотя бы один базовый случай, который не требует рекурсивный вызов, и нам нужно убедиться, что рекурсивные вызовы всегда обрабатывают меньшие версии проблемы. Что касается последнего, то мы знаем, что это верно, так как мы работаем с половиной предыдущего списка. Python Programming, 2/e 94

Разделяй и властвуй: сортировка слиянием n n В конце концов списки будут ополовиниваться пока один не станет списком из одного элемента. Что мы знаем о списке из одного элемента? Что он уже отсортирован!! У нас есть базовый случай! Когда длина списка меньше 2, то мы ничего не делаем. Мы актуализировали алгоритм merge. Sort, чтобы сделать его действительно рекурсивным… Python Programming, 2/e 95

Разделяй и властвуй: сортировка слиянием if len(nums) > 1: делим nums на две половины merge. Sort для первой половины merge. Sort для второй половины сливаем две отсортированные половины в список nums Python Programming, 2/e 96

Разделяй и властвуй: сортировка слиянием def merge. Sort(nums): # Ставим элементы nums в убывающем порядке n = len(nums) # ничего не делаем, если nums содержит 0 или 1 элементы if n > 1: # разбиваем на два листа m = n/2 nums 1, nums 2 = nums[: m], nums[m: ] # рекурсивно сортируем каждую часть merge. Sort(nums 1) merge. Sort(nums 2) # сливаем отсортированные части назад в один список merge(nums 1, nums 2, nums) Python Programming, 2/e 97

Разделяй и властвуй: сортировка слиянием n n Рекурсия тесно связана с идеей математической индукции. Она требует практики до того как станет удобной. Следуйте правилам и убедитесь, что рекурсивные цепочки достигают базовых случаев, тогда ваши алгоритмы будут работать. Python Programming, 2/e 98

Сравнение сортировок n n У нас теперь есть два алгоритма сортировки. Который следует использовать? Сложность сортировки списка зависит от размера списка. Нам нужно выяснить количество шагов в каждом из наших алгоритмов как функцию от размера списка, который нужно отсортировать. Python Programming, 2/e 99

Сравнение сортировок n n n Давайте начнём с сортировки выбором. В этом алгоритме мы начнём с нахождения элемента с наименьшим значением, затем найдём элемент с наименьшим значением среди оставшихся и так далее. Предположим, что мы начали со списка длины n. Чтобы найти элемент с наименьшим значением алгоритм должен проверить все n элементов. На следующем шаге нужно проверить остающиеся (n-1) элементов. Общее число итераций равно: n + (n-1) + (n-2) + (n-3) + … + 1 Python Programming, 2/e 100

Сравнение сортировок n n Время требуемое алгоритму выбором для сортировки списка из n элементов пропорционально сумме первых n целых чисел или. Эта формула содержит член порядка n 2 , что означает, что число шагов алгоритма пропорционально квадрату размера списка. Python Programming, 2/e 101

Сравнение сортировок n n Если список удваивается, то понадобится в четыре раза больше времени для его сортировки. Утроение размера увеличит время сортировки в 9 раз. Компьютерные специалисты называют такие алгоритмы квадратичными или n 2 алгоритмами. Python Programming, 2/e 102

Сравнение сортировок n В случае сортировки слиянием список делится на две части и каждая часть сортируется отдельно перед окончательным слиянием. Настоящим местом, где происходит сортировка, является функция слияния. Python Programming, 2/e 103

Сравнение сортировок n n Эта диаграмма показывает как сортируется список [3, 1, 4, 1, 5, 9, 2, 6]. Начиная снизу, мы должны скопировать n значений на второй уровень. Python Programming, 2/e 104

Сравнение сортировок n n Со второго на третий уровень нужно также скопировать n значений. Каждый уровень слияния требует выполнения копирования n значений. Единственным остающимся вопросом является вопрос о количестве уровней. Python Programming, 2/e 105

Сравнение сортировок n n n Мы знаем из анализа двоичного поиска, что количество уровней равно log 2 n. Следовательно, общая работа, необходимая для сортировки списка из n элементов равна n*log 2 n. Компьютерные специалисты называют такие алгоритмы n*log(n) алгоритмами. Python Programming, 2/e 106

Сравнение сортировок n n n Что будет лучше, n 2 сортировка выбором, или n *logn сортировка слиянием? Если размер списка мал, то сортировка выбором будет быстрее, потому что код проще и меньше непроизводительных затрат. Что, если n становится большим? Мы видели при обсуждении бинарного поиска, что функция log растёт очень медленно, поэтому n*log(n ) будет расти медленнее, чем n 2. Python Programming, 2/e 107

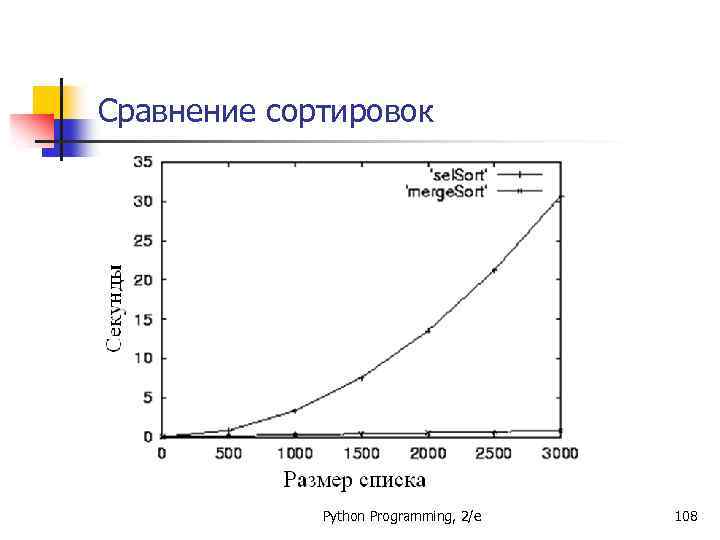
Сравнение сортировок Python Programming, 2/e 108

Трудные проблемы n n n Используя подход «разделяй и властвуй» , мы можем проектировать эффективные алгоритмы поиска и сортировки. «Разделяй и властвуй» и рекурсия это очень сильные методы в проектировании алгоритмов. Не у всех проблем имеются эффективные решения. Python Programming, 2/e 109

Ханойские башни n n n Одно элегантное применение рекурсии к задаче о Ханойских башнях или башнях Брахмы приписывают Эдуарду Люка. Имеется три столба и 64 концентрических диска в форме пирамиды. Цель – переместить диски с одного столба на другой, следуя трём правилам: Python Programming, 2/e 110

Ханойские башни n n n За раз можно двигать только один диск. Диски нельзя отставлять в «сторону» . Они всегда должны быть на одном из трёх столбов. Больший диск нельзя помещать поверх меньшего диска. Python Programming, 2/e 111

Ханойские башни n Если обозначить столбы через A, B, и C, то можно выразить алгоритм перемещения стопки дисков с A на C, используя B для временного хранения, как: Перенести диск с A на C Перенести диск с A на B Перенести диск с C на B Python Programming, 2/e 112

Ханойские башни n Давайте рассмотрим некоторые простые частные случаи – n 1 диск Перенести диск с A на C n 2 диска Перенести диск с A на B Перенести диск с A на C Перенести диск с B на C Python Programming, 2/e 113

Ханойские башни n 3 диска Чтобы переместить наибольший диск на C, нужно сначала убрать два меньших диска. Эти два меньших диска образуют пирамиду размера 2, такую задачу мы можем решать. Перенести башню размера 2 с A на B Перенести один диск с A на C Перенести башню размера 2 с B на C Python Programming, 2/e 114

Ханойские башни n Алгоритм: Перенести башню из n дисков с источника на место назначения через промежуточное место перенести башню из (n-1) дисков с источника на остающееся место перенести 1 диск с источника на место назначения перенести башню из (n-1) диска с остающегося места на место назначения n Какими должны быть базовые случаи? В конце концов мы будем передвигать башню размера 1, которую можно двигать прямо без вызова рекурсии. Python Programming, 2/e 115

Ханойские башни n n В функции move. Tower, переменная n равна размеру башни (целое), а source, dest, и temp обозначают три столба “A”, “B”, и “C”. def move. Tower(n, source, dest, temp): if n == 1: print("Перенести диск с", source, "на", dest+". ") else: move. Tower(n-1, source, temp, dest) move. Tower(1, source, dest, temp) move. Tower(n-1, temp, dest, source) Python Programming, 2/e 116

Ханойские башни n Чтобы процесс пошел, нам нужно задать значения четырём параметрам: def hanoi(n): move. Tower(n, "A", "C", "B") n >>> hanoi(3) Перенести диск Перенести диск с с с с A A C A B B A на to to to C. B. B. C. A. C. C. Python Programming, 2/e 117

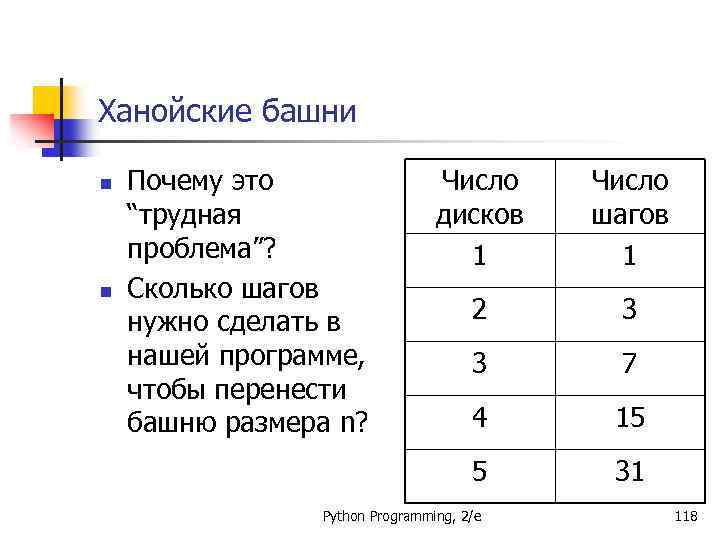Ханойские башни n n Число дисков 1 Число шагов 1 2 3 3 7 4 15 5 Почему это “трудная проблема”? Сколько шагов нужно сделать в нашей программе, чтобы перенести башню размера n? 31 Python Programming, 2/e 118

Ханойские башни n n Чтобы решить задачу размера n понадобится сделать 2 n-1 шагов. Компьютерные специалисты называют такие алгоритмы алгоритмами с экспоненциальным временем. Время выполнения экспоненциальных алгоритмов растёт очень быстро. Для перемещения 64 дисков, при условии что диск со столба на столб перемещается за секунду, и работа продолжается 24 часа в сутки, потребует 580 миллиардов лет. Текущий возраст Вселенной около 15 миллиардов лет. Python Programming, 2/e 119

Ханойские башни n n Хотя алгоритм для задачи о Ханойских башнях легко выразить, задача принадлежит к классу трудноразрешимых задач – тех, что требуют слишком много вычислительных ресурсов (времени или памяти) для решения, за исключением простейших случаев. Существуют проблемы, которые еще труднее, чем трудноразрешимые. Python Programming, 2/e 120

Проблема остановки n n Предположим, что вы хотите написать программу, которая изучает другие программы на предмет наличия в них бесконечного цикла. Мы предположим, что нам нужно также знать какие входные данные нужно задать, чтобы быть уверенными, что не комбинация самой программы и еще чего-то заставляет программу зациклиться. Python Programming, 2/e 121

Проблема остановки n n n Описание программы: n Программа: Анализатор остановки n Ввод: Python’овский программный файл. Ввод для программы. n Вывод: “OK”, если программа в конце концов остановится. “FAULTY”, если программа содержит бесконечный цикл. Вы уже видели программы, которые изучают другие программы, например Python’овский интерпретатор. Программа и её ввод можно представить цепочками символов. Python Programming, 2/e 122

Проблема остановки n n Невозможен алгоритм, который удовлетворяет вышеприведённому описанию. Это не то же самое, что сказать, что никто не в состоянии написать такую программу… Утверждение о невозможности доказывается «от противного» . Python Programming, 2/e 123

Проблема остановки n n Для доказательства «от противного» мы предполагаем противоположное тому, что пытаемся доказать и показываем, что предположение ведёт к противоречию. Первое, давайте предположим, что существует алгоритм, который определяет остановится ли программа для заданного ввода. Если это так, то можно определить следующую функцию: Python Programming, 2/e 124

Проблема остановки n n n def terminates(program, input. Data): # программа и input. Data цепочки символов # Возвращает true, если программа остановится, # когда запускается с input. Data в качестве # входных данных Если бы у нас была бы такая функция, то мы могли бы написать следующую программу : # turing. py def terminates(program, input. Data): # программа и input. Data цепочки символов # Возвращает true, если программа остановится, # когда запускается с input. Data в качестве # входных данных Python Programming, 2/e 125

Проблема остановки def main(): # Читаем программу со стандартного ввода lines = [] print("Напечатай в программе (напечатай ‘готово' для выхода). ") line = input("") while line != "готово": lines. append(line) line = input("") test. Prog = "n". join(lines) # Если программа останавливается на себе как на # вводе идём на бесконечный цикл if terminates(test. Prog, test. Prog): while True: pass # оператор pass ничего не # делает Python Programming, 2/e 126

Проблема остановки n n Программа называется “turing. py” в честь Алана Тьюринга, британского математика, которого считают «отцом информатики» . Давайте посмотрим на программу шаг-зашагом, чтобы определить, что она делает … Python Programming, 2/e 127

Проблема остановки n n n Программа turing. py сначала читает программу, напечатанную пользователем, используя цикл с ограничителем. Метод join сцепляет строки вместе, ставя между строками символ новой строки (n). Это создаёт многостроковую цепочку символов, представляющую программу, которая была введена. Python Programming, 2/e 128

Проблема остановки n n n Программа turing. py затем использует введённую программу не только как программу для тестирования, но и как ввод для тестирования. Другими словами, мы смотрим, остановится ли программа, которую напечатали, если ей дать саму себя в качестве ввода. Если программа-ввод остановится, то программа turing. py входит в бесконечный цикл. Python Programming, 2/e 129

Проблема остановки n n Зададим вопрос: что случится, если мы запустим программу turing. py, и воспользуемся программой turing. py как вводом? Остановится ли turing. py? Python Programming, 2/e 130

Проблема остановки n n В функции terminates программа turing. py будет оценена, чтобы увидеть остановится ли она или нет. Возможны два случая: n Программа turing. py остановится, если ей дать саму себя в качестве ввода n Тогда функция Terminates возвращает true n Тогда, turing. py входит в бесконечный цикл n Поэтому turing. py не останавливается, противоречие Python Programming, 2/e 131

Проблема остановки n Программа Turing. py не останавливается n n Функция terminates возвращает false Если terminates false, то наша программа выходит из программы Когда программа выходит из программы, она останавливается, противоречие Существование функции terminates ведёт к противоречию, поэтому мы заключаем, что существование такой функции невозможно. Python Programming, 2/e 132

Заключение n n n Информатика больше чем программирование Самый важный компьютер для любого вычисляющего профессионала расположен между его ушами. Вы должны стать компьютерным специалистом. Python Programming, 2/e 133