Скачать презентацию Программирование 1 Лекция 7 Вычисления с вещественными числами
Л 07 13окт Вещ тип.ppt
- Количество слайдов: 35
Программирование 1 Лекция 7 Вычисления с вещественными числами (продолжение): Вычисления с вещественными числами и машинное эпсилон 13. 10. 2011 Вычисления с вещественными числами 2 1
Вычисления с вещественными числами и машинное эпсилон Вещественные числа в форме с плавающей точкой (floating point): x = ± (a 1 b – 1 + a 2 b – 2 + …+ at b –t ) b p , (*) ai {0. . (b 1)} при i = 1, 2, …, t. Позиционная система счисления с основанием b. Пример: b = 10 – десятичная система. x = ± (a 110– 1 + a 2 10– 2 + …+ at 10–t) 10 p , (*) ai {0. . 9} при i = 1, 2, …, t. 2. 71828 = 0. 271828*101 = 27. 1828*10 1 = 0. 0271828*102 Представление не единственно. Нормализованный вид при a 1 0 : 0. 271828*101 13. 10. 2011 Вычисления с вещественными числами 2 2
Вычисления с вещественными числами и машинное эпсилон Вещественные числа в форме с плавающей точкой (floating point) в двоичной системе: x = ± (a 12– 1 + a 22– 2 + …+ at 2–t ) 2 p , (*) ai {0, 1} при i = 1, 2, …, t. нормализованный вид: a 1 = 1 (такое представление единственно). Число = ±(a 12– 1 + a 22– 2 + …+ at 2–t) - мантисса числа x (или дробная часть). Число бит t – разрядность мантиссы. Целое число p – двоичный порядок. L p U. Система чисел F(t, L, U) в представлении (*) задается параметрами t, L, U. 13. 10. 2011 Вычисления с вещественными числами 2 3
Особенности системы F (t, L, U) В системе F(t, L, U) представимо конечное множество положительных чисел, а именно 2 t – 1(U – L + 1). Если учесть отрицательные числа и 0, то всего чисел 2 2 t – 1(U – L + 1) + 1. Пример. t = 3, L = 1, U = 2. Всего чисел 2*16 + 1 = 33, из них положительных 16. 13. 10. 2011 Вычисления с вещественными числами 2 4
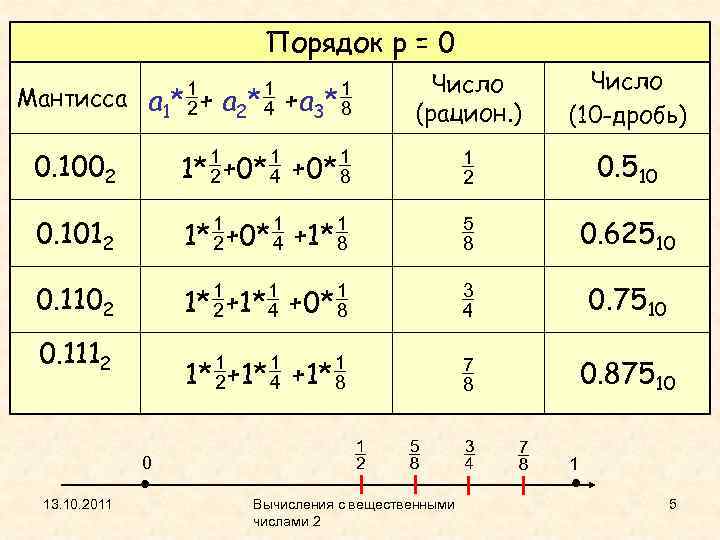Порядок p = 0 Мантисса a * +a * 1 2 3 Число (рацион. ) Число (10 -дробь) 0. 1002 1* +0* 0. 510 0. 1012 1* +0* +1* 0. 62510 0. 1102 1* +0* 0. 7510 1* +1* 0. 87510 0. 1112 0 13. 10. 2011 Вычисления с вещественными числами 2 1 5
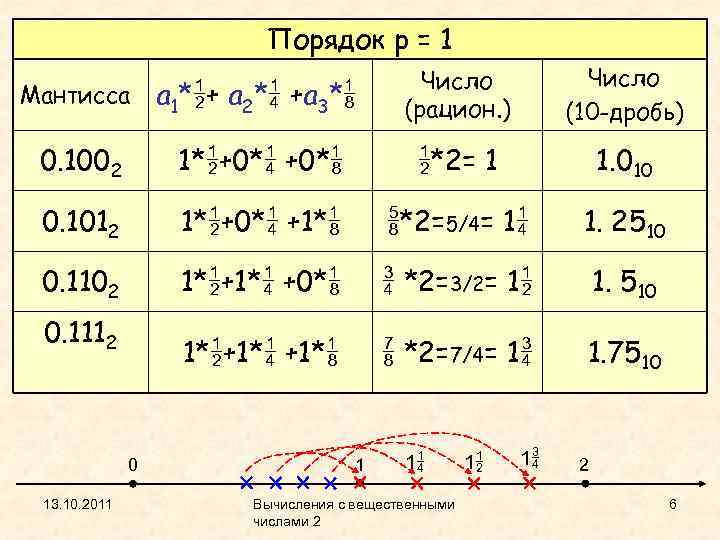Порядок p = 1 Число (10 -дробь) Мантисса a 1* + a 2* +a 3* Число (рацион. ) 0. 1002 1* +0* *2= 1 1. 010 0. 1012 1* +0* +1* *2=5/4= 1 1. 2510 0. 1102 1* +0* *2=3/2= 1 1. 510 1* +1* *2=7/4= 1 1. 7510 0. 1112 0 13. 10. 2011 1 1 Вычисления с вещественными числами 2 1 1 2 6
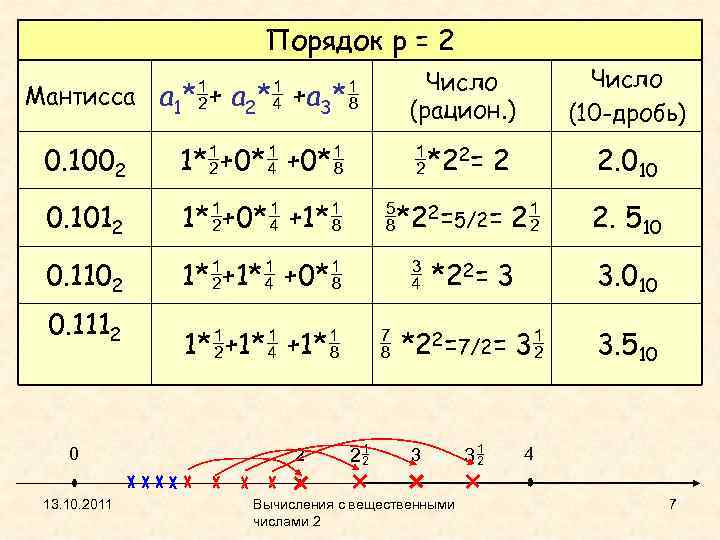Порядок p = 2 Мантисса a 1* + a 2* +a 3* Число (рацион. ) Число (10 -дробь) 0. 1002 1* +0* *22= 2 2. 010 0. 1012 1* +0* +1* *22=5/2= 2 2. 510 0. 1102 1* +0* *22= 3 3. 010 1* +1* *22=7/2= 3 3. 510 0. 1112 0 13. 10. 2011 2 2 3 Вычисления с вещественными числами 2 3 4 7
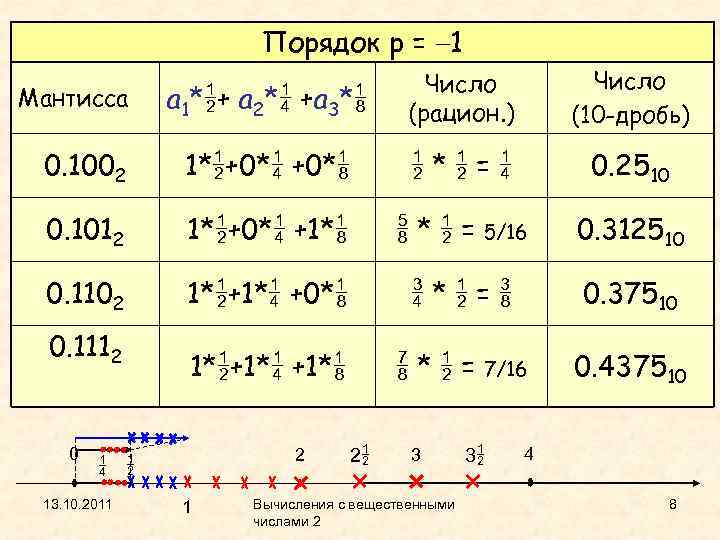Порядок p = 1 a 1* + a 2* +a 3* Число (рацион. ) Число (10 -дробь) 0. 1002 1* +0* * = 0. 2510 0. 1012 1* +0* +1* * = 5/16 0. 312510 0. 1102 1* +0* * = 0. 37510 1* +1* * = 7/16 0. 437510 Мантисса 0. 1112 0 2 13. 10. 2011 1 2 3 Вычисления с вещественными числами 2 3 4 8
Особенности 1) Конечное множество (33) 2) Максимальное по величине число = (1 – 2–t) 2 U (3 ). Попытка вычислить число x > (или x < – ) –ошибка переполнения. 3) В окрестности нуля – «зазор» ( ), отсутствуют числа системы F (t, L, U). Самое маленькое положительное число = 2 L – 1 ( ). Попытка вычислить число x 0, такое, что |x| < , - ошибка антипереполнения или исчезновения порядка. 4) Неравномерность на оси. В интервале 1 x < 2 зазор 21 – t. В интервале 2 p – 1 x < 2 p зазор 2 p – t. 13. 10. 2011 Вычисления с вещественными числами 2 9
Абсолютная ошибка представления числа x числом fl(x) системы чисел F(t, L, U) есть • x = |fl(x) – x| и x 2 p – t при округлении отбрасыванием всех цифр (at + 1, at + 2, …) после at • x 2 p – t – 1 при округлении к ближайшему числу fl(x). Относительная ошибка представления числа x есть (x) = x / |x|. Значение (x) не зависит от интервала и (x) или (x) 2– 1 соответственно при округлении отбрасыванием или при округлении “к ближайшему”. 13. 10. 2011 Вычисления с вещественными числами 2 10
Особенности вычислений с вещественными числами. Дополнение. Нарушение ассоциативности сложения: (a + b) + c a + (b + c) Следствие: результат зависит от порядка суммирования Пример: 5/16 + (2 1) (5/16 + 2) 1 1) 5/16 + (2 1) = 5/16 + 1= 0. 101*2 1 + 0. 100*21 = = (0. 101*2 2 + 0. 100*20) * 21= = (0. 00101*20 + 0. 100*20) * 21= = (0. 001[01] + 0. 100) * 21= (0. 101[01]) * 21= = 0. 101* 21 = 5/4 = 1. Точный результат = 21/16 = 1+5/16 13. 10. 2011 Вычисления с вещественными числами 2 11
2) 5/16 + 2 = 0. 101*2 1 + 0. 100*22 = = (0. 101*2 3 + 0. 100*20) * 22= = (0. 000101*20 + 0. 100*20) * 22= = (0. 000[101] + 0. 100) * 22= (0. 100[101]) * 22 = 0. 100* 22 = 2 в режиме «отбрасывания» = 0. 101* 22 = 2 в режиме округления 1 в режиме «отбрасывания» (5/16 + 2) 1 = 1 в режиме округления Т. о. 1 1 и 1 1 1 13. 10. 2011 Вычисления с вещественными числами 2 1+5/16 12
Стандартные формы чисел с плавающей точкой: Стандарт 754 (IEEE) – 1985 г. – «плавающая точка IEEE» • формат одинарной точности (в B-Pascal – тип single, в С/С++ - float); • формат двойной точности (в BP и в – тип С/С++ double); • формат расширенной (повышенной) точности (в BP – тип Extended ). (long double ? ) 13. 10. 2011 Вычисления с вещественными числами 2 13
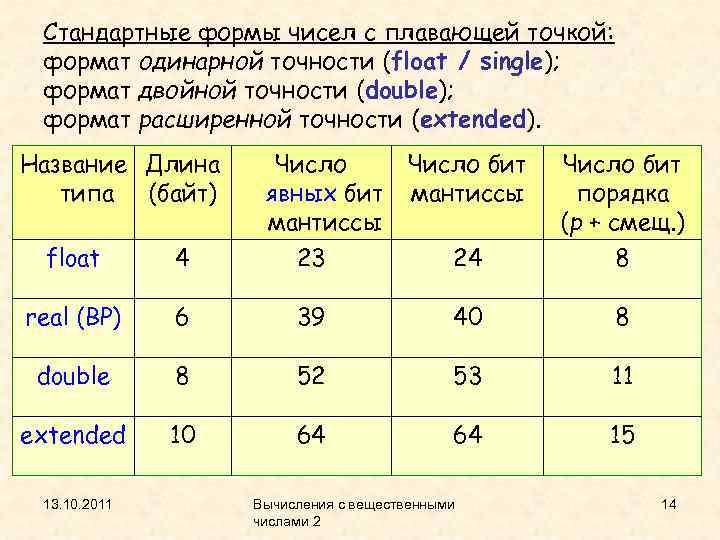Стандартные формы чисел с плавающей точкой: формат одинарной точности (float / single); формат двойной точности (double); формат расширенной точности (extended). Название Длина типа (байт) Число явных бит мантиссы Число бит порядка (p + смещ. ) float 4 23 24 8 real (BP) 6 39 40 8 double 8 52 53 11 extended 10 64 64 15 13. 10. 2011 Вычисления с вещественными числами 2 14
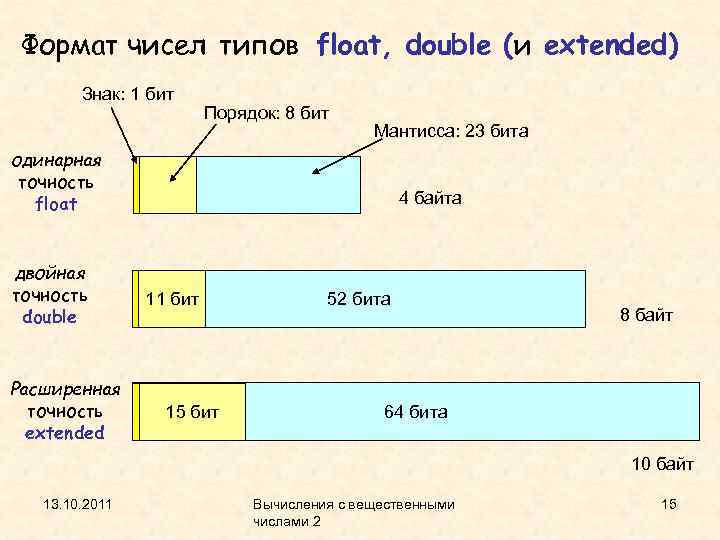Формат чисел типов float, double (и extended) Знак: 1 бит Порядок: 8 бит Мантисса: 23 бита одинарная точность float двойная точность double Расширенная точность extended 4 байта 11 бит 15 бит 52 бита 8 байт 64 бита 10 байт 13. 10. 2011 Вычисления с вещественными числами 2 15
Машинное эпсилон В качестве характеристики точности представления вещественных чисел в ЭВМ используют так называемое машинное эпсилон, определяемое как eps = min { >0: fl ( + 1) > 1 }. Эта величина учитывает особенности реализации системы F(t, L, U) в конкретном типе компьютера. Проблема переносимости ПО (библиотек). 0. 10… 001*21 1 пусто 13. 10. 2011 eps Вычисления с вещественными числами 2 16
Встроенное в программу ( «эмпирическое» ) вычисление машинного эпсилон typedef float real; // (long) double real eps, eps. P 1, epsil; eps 1. cpp int i; i = 0; eps = 1. 0; eps. P 1 = 2. 0; while (eps. P 1 > 1. 0) { // eps=2^(-i) && (1+eps>1) eps = eps * 0. 5; eps. P 1 = eps + 1. 0; i = i + 1; } //end: eps=2^(-i) && !(1+eps>1) && (1+2*eps>1) epsil = 2. 0 * eps; 13. 10. 2011 Вычисления с вещественными числами 2 17
Встроенное в программу ( «эмпирическое» ) вычисление машинного эпсилон (найди отличия!) typedef float real; // (long) double real eps, epsil; eps 2. cpp int i; i = 0; eps = 1. 0; while (eps+1. 0 > 1. 0) { // eps=2^(-i) && (1+eps>1) eps = eps * 0. 5; i = i + 1; } //end: eps=2^(-i) && !(1+eps>1) && (1+2*eps>1) epsil = 2. 0 * eps; Анализ выполнения (eps 1. cpp b, eps 2. cpp) и интерпретация результатов 13. 10. 2011 Вычисления с вещественными числами 2 18
Рекомендации программисту 1. Память более важна, чем точность одинарная точность float (single) 2. Точность более важна, чем память двойная точность double (long double) 3. [Расширенная точность Extended только в специальных случаях (с самостоятельным контролем точности программистом) – в С++ не актуально] 13. 10. 2011 Вычисления с вещественными числами 2 19
Полезное отступление Вывод результатов работы программы в файл Что дает? 1) Возможность документировать (сохранить) для дальнейшего анализа, отчетности и т. п. 2) Возможность анализировать с большим полем обзора, чем окно консоли (+ масштабирование) 3) Возможность редактировать (модифицировать, вырезать, использовать в других документах – например, в лекциях - и т. п. ) 4) Возможность обрабатывать другими программами (например, Exel – таблицы, графики, диаграммы и т. п. ) 13. 10. 2011 Вычисления с вещественными числами 2 20
Рекомендации книг по C++ См. файл «книги С++. ppt» 13. 10. 2011 Вычисления с вещественными числами 2 21
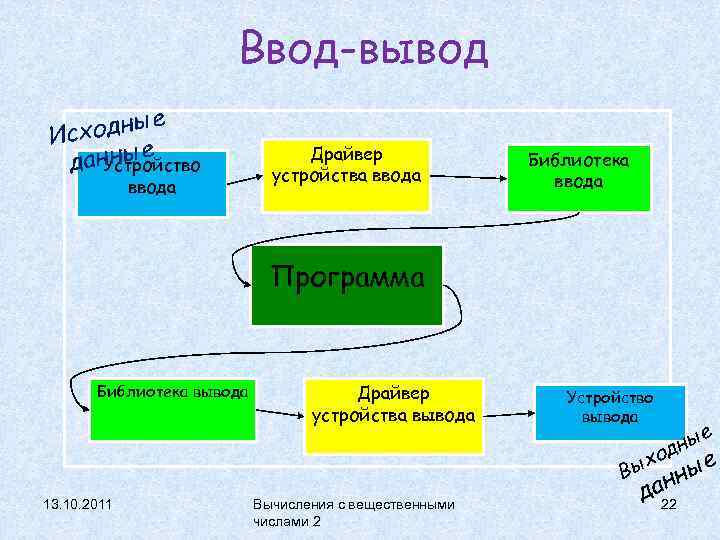Ввод-вывод одные Исх е данны Устройство ввода Драйвер устройства ввода Библиотека ввода Программа Библиотека вывода 13. 10. 2011 Драйвер устройства вывода Вычисления с вещественными числами 2 Устройство вывода е ы дн о ых ные В н да 22
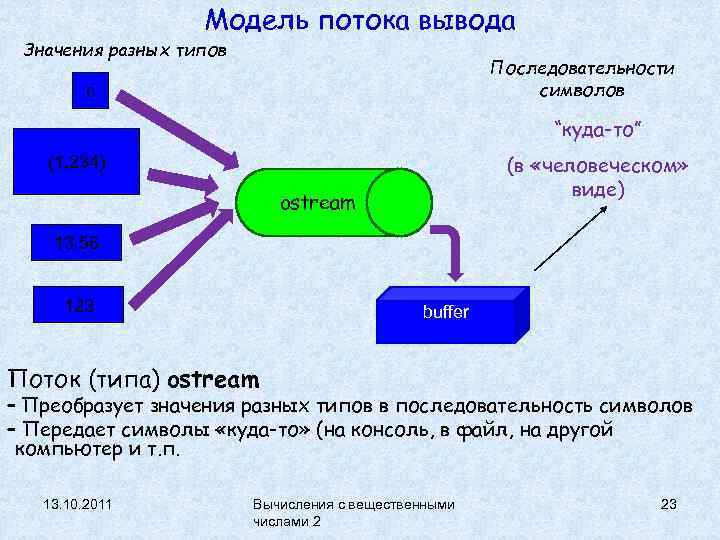Модель потока вывода Значения разных типов Последовательности символов c “куда-то” (в «человеческом» виде) (1, 234) ostream 13. 56 123 buffer Поток (типа) ostream – Преобразует значения разных типов в последовательность символов – Передает символы «куда-то» (на консоль, в файл, на другой компьютер и т. п. 13. 10. 2011 Вычисления с вещественными числами 2 23
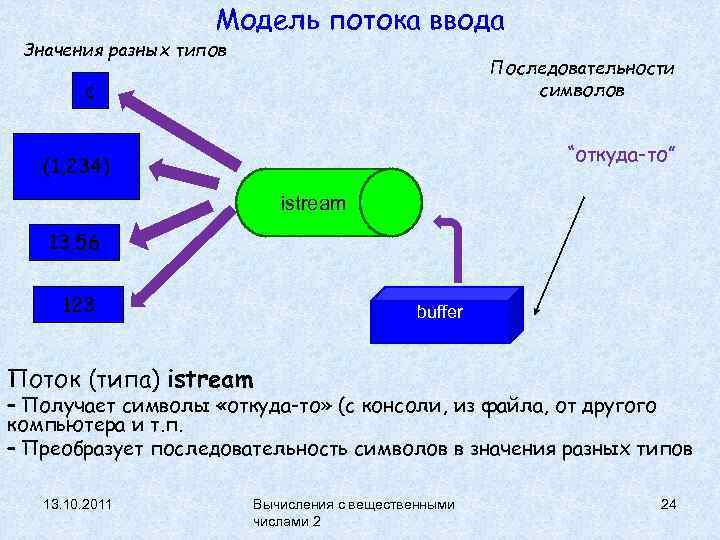Модель потока ввода Значения разных типов Последовательности символов c “откуда-то” (1, 234) istream 13. 56 123 buffer Поток (типа) istream – Получает символы «откуда-то» (с консоли, из файла, от другого компьютера и т. п. – Преобразует последовательность символов в значения разных типов 13. 10. 2011 Вычисления с вещественными числами 2 24
Нами уже использовались Стандартные потоки (из библиотеки iostream): • для ввода – поток cin (типа istream) • для вывода – поток cout (типа ostream) Подключение в программе: #include
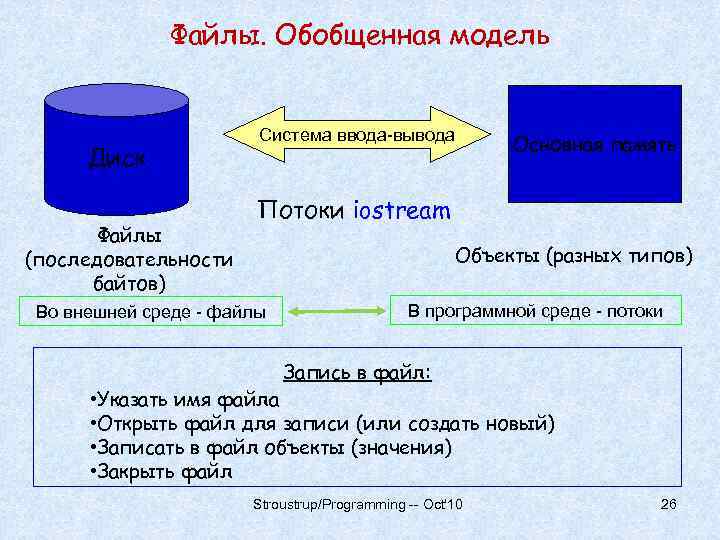Файлы. Обобщенная модель Диск Файлы (последовательности байтов) Система ввода-вывода Основная память Потоки iostream Объекты (разных типов) Во внешней среде - файлы В программной среде - потоки Запись в файл: • Указать имя файла • Открыть файл для записи (или создать новый) • Записать в файл объекты (значения) • Закрыть файл Stroustrup/Programming -- Oct'10 26
#include
Демонстрация программ про машинное ЭПСИЛОН Программы про машинное эпсилон см. в таком порядке: eps 1. cpp – без вывода в файл eps 2. cpp – без вывода в файл + некорректность float==double eps 3 file. cpp – c выводом в файл для float eps 3 d_file. cpp – c выводом в файл для double eps 3 f_file_err. cpp – c выводом в файл для float + некорректность float==double 13. 10. 2011 Вычисления с вещественными числами 2 28
Конец отступления про вывод в файл 13. 10. 2011 Вычисления с вещественными числами 2 29
Анализ примера с вычислением sin x С выводом в файл! См. sin 3 f_fil. cpp Epsilon = 1 e-005 тип float x(0)=5. 2359879017 e-001 x(1)=6. 8067841530 e+000 x(2)=1. 3089969635 e+001 x(3)=1. 9373155594 e+001 x(4)=2. 5656341553 e+001 x(5)=3. 1939527512 e+001 S(x)=+5. 00000 e-001 S(x)=+5. 0000530481 e-001 S(x)=+4. 9994155765 e-001 S(x)=+2. 5872075558 e-001 S(x)=-4. 4802917480 e+002 S(x)=-1. 1173758594 e+005 sin sin sin x=+5. 00000 e-001 x=+5. 0000005960 e-001 x=+5. 0000023842 e-001 x=+5. 0000077486 e-001 x=+5. 0000131130 e-001 x=+5. 0000190735 e-001 n= n= n= f(x) = sin(x) = Σi = 0. . . ∞ (– 1)ix 2 i + 1/ (2 i + 1)! sin(x) = 13. 10. 2011 Вычисления с вещественными числами 2 30 3 13 22 30 39 47
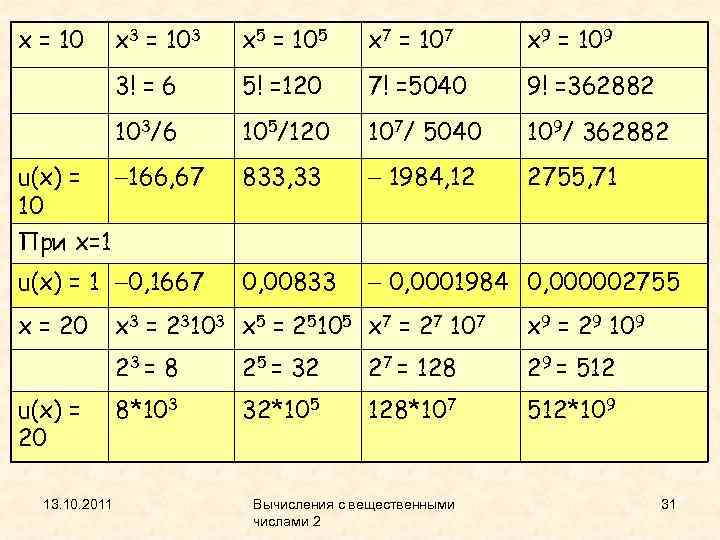x = 10 x 5 = 105 x 7 = 107 x 9 = 109 3! = 6 5! =120 7! =5040 9! =362882 103/6 u(x) = 10 x 3 = 103 105/120 107/ 5040 109/ 362882 166, 67 833, 33 1984, 12 2755, 71 0, 00833 0, 0001984 0, 000002755 При x=1 u(x) = 1 0, 1667 x = 20 13. 10. 2011 x 9 = 29 109 23 = 8 u(x) = 20 x 3 = 23103 x 5 = 25105 x 7 = 27 107 25 = 32 27 = 128 29 = 512 8*103 32*105 128*107 512*109 Вычисления с вещественными числами 2 31
Машинное эпсилон и точность вычислений (комментарии и примеры) y x Параметр точности - характеристика абсолютной или относительной ошибки (точности); см. exponenta. cpp 13. 10. 2011 Вычисления с вещественными числами 2 32
Пример. Проверка ортогональности прямых Отложено Изменение масштаба : * < * > или * > * < 13. 10. 2011 Вычисления с вещественными числами 2 33
вектор нормали прямой Отложено ортогональность прямых 13. 10. 2011 Вычисления с вещественными числами 2 34
КОНЕЦ ЛЕКЦИИ КОНЕЦ ЛЕКЦИИ 13. 10. 2011 Вычисления с вещественными числами 2 35