Программирование 1 Лекция 6 Часть 1 1 Кратко

Программирование 1 Лекция 6 Часть 1 1. Кратко: доп. примеры из лекции 5 2. Схема итерации (продолжение). 3. Вычисления с вещественными числами: • Рекуррентные вычисления суммы ряда • Вычисления с вещественными числами и машинное эпсилон (в части 2) 06. 10. 2011 Схема итерации 2 1

Подытожим рассмотренные примеры: 06. 10. 2011 Схема итерации 2 2

Обобщение – схема итерации (iteratio – повторение) Многие вычисления укладываются в следующую схему: X = X 0; while (B(X)) { X = f (X) } * где X – множество переменных программы, X 0 – их начальные значения, B(X) – булевская функция (предикат) от переменных X, а f – некоторая функция преобразования переменных. В соответствии с семантикой цикла while–do предикат B(X) – условие продолжения цикла. Пояснить смысл слов «схема» и её интерпретация. 06. 10. 2011 Схема итерации 2 3

Например (1), при вычислении fact (n): X = (x, y), пояснить, почему не y*x X 0 = (0, 1), B(X) (x < n), f: (x, y) (x + 1, y*(x+1)) (2) Если положить X = (u, v), u = a; v = b; X 0 = (a, b), while (v != 0) { B(X) (v <> 0), r =u%v; f: (u, v) (v, u mod v), u =v; то получим алгоритм Евклида v =r; } 06. 10. 2011 Схема итерации 2 4

Конец примера (схема и интерпретация) Вернемся к схеме итерации X = X 0; while (B(X)) { X = f (X) } * Все конкретные программы, порождаемые схемой *, обладают некоторыми общими свойствами. 06. 10. 2011 Схема итерации 2 5

Пусть цикл while-do в (*) завершился за n шагов и переменные x принимали последовательно значения x 0, x 1, …, xn – 1, xn, тогда последовательность {xi} (i [0; n]) обладает свойствами: 1. 2. 3. 4. xi = f (x i – 1) для всех i [1; n]; xi ≠ xj при i ≠ j и i, j [0; n]; B(xi) для всех i [0; n – 1]; not B(xn). 06. 10. 2011 Схема итерации 2 6

Замечания • Свойство 1: xi = f (x i – 1) для всех i [1; n] - следует из семантики оператора присваивания x =f(x). • Свойство 2: xi ≠ xj при i ≠ j и i, j [0; n] - выражает необходимое условие завершения цикла. • Свойства 3 и 4 следуют из семантики конструкции цикла while. • Итерации заканчиваются, если существует n, соответствующее свойству 4: not B(xn). • При этом значение n является наименьшим из всех таких значений, что определяется свойством 3: B(xi) для всех i [0; n – 1] 06. 10. 2011 Схема итерации 2 7

Иногда эти свойства схемы * рассматривают как “Теорему о линейном просмотре”, поскольку такая программа осуществляет поиск среди значений x 0, xi = f(xi – 1), при i > 0 , значения xi с минимальным индексом i ≥ 0, при котором истинно not B(xi). x 0 06. 10. 2011 Схема итерации 2 xn 8

Резюме Очевидно, что схема * является слишком общей и в таком виде малоинтересна. Любой цикл while-do можно рассматривать как реализацию схемы *. Интерес представляют, как правило, частные случаи этой схемы. Однако и в таком виде она является подходящей формой программ, основанных на рекуррентных соотношениях: xi = f (xi – 1) 06. 10. 2011 Схема итерации 2 10

Рекомендации по разработке циклических программ, основанных на рекуррентных соотношениях 1. Сформулировать математическую модель задачи, включающую математические объекты и рекуррентные соотношения, связывающие их значения на разных шагах вычислений. 2. Определить переменные, которые будут использоваться в программе и представлять математические объекты, введенные в п. 1. 3. Определить условие продолжения цикла while-do; записать инициализацию и тело цикла. 4. Записать для ключевых точек цикла утверждения, связывающие переменные программы и определенные ранее математические объекты. 06. 10. 2011 Схема итерации 2 11

Вычисления с вещественными числами: • • Рекуррентные вычисления суммы ряда Вычисления с вещественными числами и машинное эпсилон 06. 10. 2011 Схема итерации 2 12

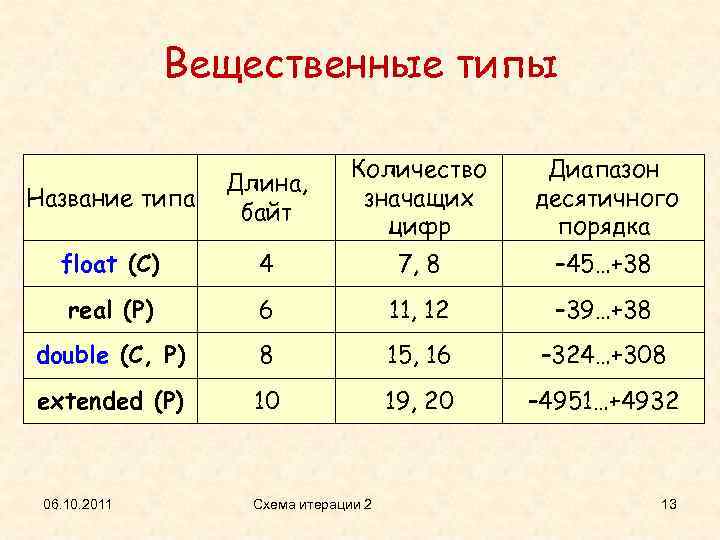Вещественные типы Название типа Длина, байт Количество значащих цифр Диапазон десятичного порядка float (C) 4 7, 8 – 45…+38 real (P) 6 11, 12 – 39…+38 double (C, P) 8 15, 16 – 324…+308 extended (P) 10 19, 20 – 4951…+4932 06. 10. 2011 Схема итерации 2 13

Рекуррентные вычисления суммы ряда Пусть задана последовательность членов ряда u 0, u 1, …, un …. Рассмотрим последовательность частичных сумм S 0, S 1, …, Sn, …, где Si = j = 0. . . i uj Если , то говорят, что ряд сходится и записывают это в виде S = j = 0. . . ∞ uj. 06. 10. 2011 Схема итерации 2 14

Задача приближенного вычисления суммы ряда Вычислить частичную суммы Sn, где номер последнего слагаемого n определяется дополнительным требованием. Например, при заданном (обычно малом) числе > 0 номер n таков, что n = min{i > 0 : |ui| ≤ }. Иначе говоря, для всех 0 i < n имеем |ui| > , а n номер последнего слагаемого в частичной сумме Sn и un . Соотношение |ui| > можно использовать как условие продолжения цикла вычисления суммы ряда. 06. 10. 2011 Схема итерации 2 15

Если слагаемые можно вычислить рекуррентно: ui = f (u i 1), то вычислить сумму Sn можно так: // i = 0 s = s 0; u = u 0; B(s, u, ) (|ui| > }) while (B(s, u, )) { // (s=S(i)) & (u=u(i)) & (i

Пример: Вычислить частичную сумму сходящегося бесконечного ряда разложения функции, f(x) = sin(x) = Σi = 0. . . ∞ (– 1)ix 2 i + 1/ (2 i + 1)!, x R. sin(x) = ui = (–x 2/(2 i + 1))) ui – 1; ui = (–x 2/di) ui – 1; d 0 = 0; dd 0 = – 2 06. 10. 2011 Схема итерации 2 17

sin 1. cpp // Вычисления по заданным x и Epsil i = 0; //. . . dd = -2; d = 0; t = x; s = x; w = -x*x; //s=s(i) & t=t(i) & i=0 while (fabs(t) > epsil) { // s=s(i) & t=t(i) & d=d(i) & dd=dd(i) & i

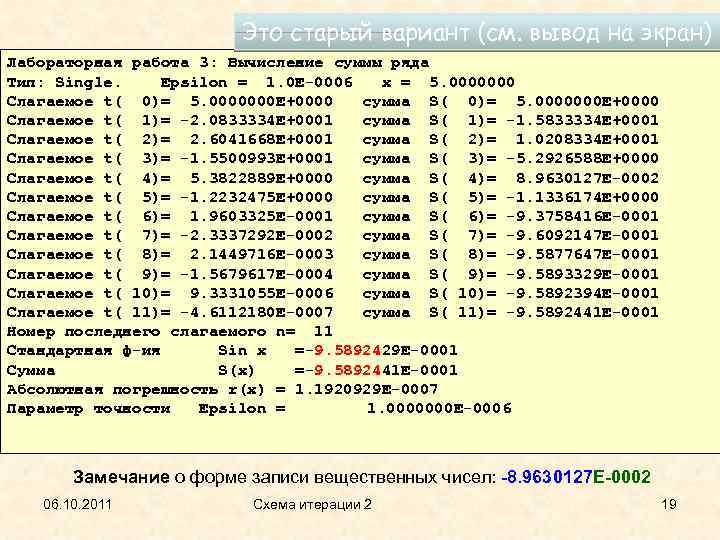Это старый вариант (см. вывод на экран) Лабораторная работа 3: Вычисление суммы ряда Тип: Single. Epsilon = 1. 0 E-0006 x = 5. 0000000 Слагаемое t( 0)= 5. 0000000 E+0000 сумма S( 0)= 5. 0000000 E+0000 Слагаемое t( 1)= -2. 0833334 E+0001 сумма S( 1)= -1. 5833334 E+0001 Слагаемое t( 2)= 2. 6041668 E+0001 сумма S( 2)= 1. 0208334 E+0001 Слагаемое t( 3)= -1. 5500993 E+0001 сумма S( 3)= -5. 2926588 E+0000 Слагаемое t( 4)= 5. 3822889 E+0000 сумма S( 4)= 8. 9630127 E-0002 Слагаемое t( 5)= -1. 2232475 E+0000 сумма S( 5)= -1. 1336174 E+0000 Слагаемое t( 6)= 1. 9603325 E-0001 сумма S( 6)= -9. 3758416 E-0001 Слагаемое t( 7)= -2. 3337292 E-0002 сумма S( 7)= -9. 6092147 E-0001 Слагаемое t( 8)= 2. 1449716 E-0003 сумма S( 8)= -9. 5877647 E-0001 Слагаемое t( 9)= -1. 5679617 E-0004 сумма S( 9)= -9. 5893329 E-0001 Слагаемое t( 10)= 9. 3331055 E-0006 сумма S( 10)= -9. 5892394 E-0001 Слагаемое t( 11)= -4. 6112180 E-0007 сумма S( 11)= -9. 5892441 E-0001 Номер последнего слагаемого n= 11 Стандартная ф-ия Sin x =-9. 5892429 E-0001 Сумма S(x) =-9. 5892441 E-0001 Абсолютная погрешность r(x) = 1. 1920929 E-0007 Параметр точности Epsilon = 1. 0000000 E-0006 Замечание о форме записи вещественных чисел: -8. 9630127 E-0002 06. 10. 2011 Схема итерации 2 19

Эксперимент (!) sin 2. cpp x = 4*atan(1. ); const real pi=x; x = pi/6; j = 0; while (j<=5) { cout << “===" << " аргумент <" << j << "> = " << x << endl; ВЫЧИСЛЕНИЯ ПО АЛГОРИТМУ } cout << "S(x)=" << s << " : : sin x =" << sin(x) << " n= " << i << endl; x = x + 2. *pi; j++; Демонстрация (float / double, фоматирование) 06. 10. 2011 Схема итерации 2 20

КОНЕЦ ЛЕКЦИИ КОНЕЦ ЛЕКЦИИ 6. 1 06. 10. 2011 Схема итерации 2 21