Программирование 1 Лекция 4 Программирование циклов Схема итерации

Программирование 1 Лекция 4 Программирование циклов. Схема итерации (продолжение). 22. 09. 2011 Схема итерации 1

Пример 2 Рассмотрим готовую программу (фрагмент) // n 1 p = 1; k = n; while (k > 0) { p = p *k ; k = k 1 ; } Что здесь вычисляется? Как это понять (проанализировать)? 22. 09. 2011 Схема итерации 2

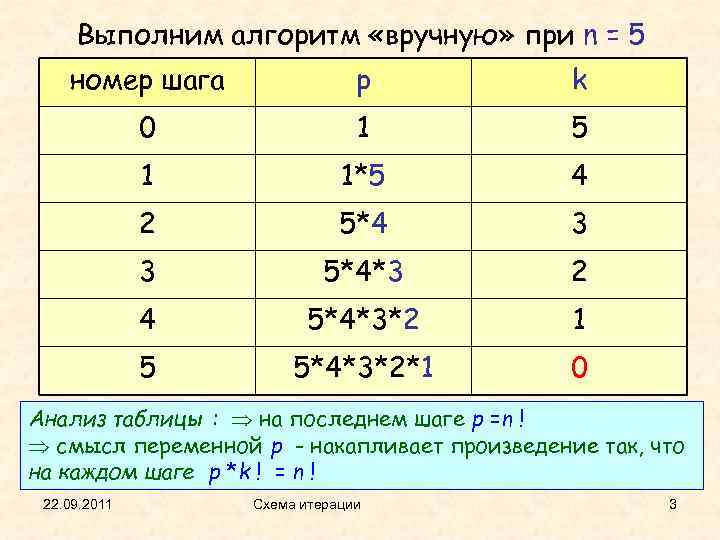Выполним алгоритм «вручную» при n = 5 номер шага p k 0 1 5 1 1*5 4 2 5*4 3 3 5*4*3 2 4 5*4*3*2 1 5 5*4*3*2*1 0 Анализ. Примечание: про замену условия продолжения !цикла на k>1 таблицы на последнем шаге p =n смысл переменной p - накапливает произведение так, что на каждом шаге p *k ! = n ! 22. 09. 2011 Схема итерации 3

Итак, видимо, вычисляется n! Предположим, что «индуктивное» утверждение есть p *k ! = n ! // n 1 p = 1; k = n; // Утв 1: ? while (k > 0) { //Утв 1: (p *k ! = n !) & (0 k n) // Утв 2: ? //Утв 2: (p *k ! = n!) & (0 < k n) p = p*k; k = k 1; //Утв 3: (p*k ! = n !) & (0 k < n) // Утв 3: ? } n! = p*k*(k-1)! p*k ! = n! //p=n ! 22. 09. 2011 Схема итерации 4

Ещё примеры программ, основанных на рекуррентной схеме. Пример 3 Дано: n > 0 Вычислить: Пусть Тогда Si = S i 1 + i ! Будем вычислять xi = xi-1 + 1 (аргумент) yi = yi-1* xi (функция fact(xi)) Si = Si-1 + yi (сумма) и x 0=0, y 0=1, S 0=0. 22. 09. 2011 Схема итерации 5

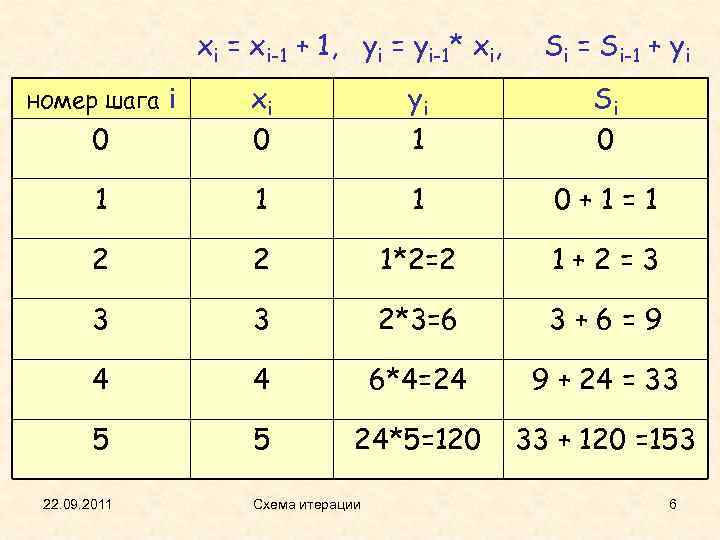xi = xi-1 + 1, yi = yi-1* xi, номер шага i Si = Si-1 + yi 0 xi 0 yi 1 Si 0 1 1 1 0+1=1 2 2 1*2=2 1+2=3 3 3 2*3=6 3+6=9 4 4 6*4=24 9 + 24 = 33 5 5 24*5=120 33 + 120 =153 22. 09. 2011 Схема итерации 6

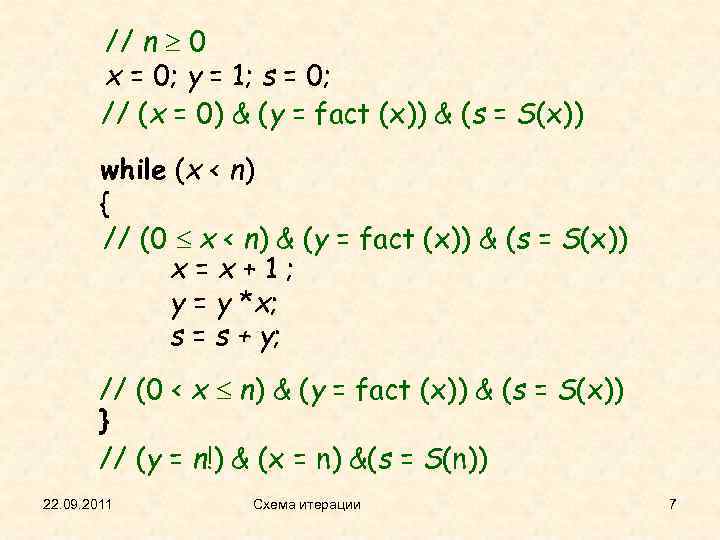// n 0 x = 0; y = 1; s = 0; // (x = 0) & (y = fact (x)) & (s = S(x)) while (x < n) { // (0 x < n) & (y = fact (x)) & (s = S(x)) x = x + 1 ; y = y *x; s = s + y; // (0 < x n) & (y = fact (x)) & (s = S(x)) } // (y = n!) & (x = n) &(s = S(n)) 22. 09. 2011 Схема итерации 7

Демонстрация программы sum_f. cpp 22. 09. 2011 Схема итерации 8

Пример 4. Для заданного целого n ≥ 0 вычислить S (n) = i = 0. . . n a (i ) , где a (i ) = A(i | m) , и m — заданное целое (m ≥ n) , а A(i | m) = m! / (m–i)! = m (m– 1) … (m – i + 1). Например: m = 5; n = 3. A(i | 5) = 5! / (5–i)! S (n) = i =0. . . 3 а (i ) = = i=0. . . 3 A(i | 5) = а(0)+ а(1)+ а(2)+ а(3) = = A(0| 5) + A(1| 5) + A(2| 5) + A(3| 5) = = 5! / 5! + 5! / 4! + 5! / 3! + 5! / 2! = = 1 + 5*4*3 = 1 + 5 + 20 + 60 = 86 22. 09. 2011 Схема итерации 9

S (i ) = S (i 1) + a (i ); i =1, …, n; S (0) = A(0| m) = 1; a (i ) = A(i | m) = m! / (m–i)! a (i 1) = A(i 1 | m) = m! / (m – i + 1)! Хотим вычислять a (i ) = a (i 1) * нечто, т. е. нечто = a (i ) / a (i 1) = = (m! / (m–i)!) / (m! / (m – i + 1)!) = = (m – i + 1)! / (m–i)! = (m – i + 1) Т. о. a (i ) = a (i 1) * (m – i + 1) В программе: • слагаемое a (i ) переменная a, • номер слагаемого i переменная i, • формируемая сумма S (i ) переменная s. 22. 09. 2011 Схема итерации 10

//n 0, S(i)=a(0)+. . . +a(i), a(i) = a(i 1) * (m – i + 1) i = 0; a = 1; s = 1; //(a = a(0) = 1) & (s = S(0) = 1) & (i = 0) while ( i < n ) { // (a=a(i)) & (s=S(i)) & (0 i < n) i = i+1; a = a* (m – i + 1); s = s + a; //(a=a(i)) & (s=S(i)) & (0 < i n) } //(a=a(n)) & (s=S(n)) & (0 i = n) 22. 09. 2011 Схема итерации 11

Тот же пример: m = 5; n = 3. i s 0 1 1*5=5 1+5=6 2 5*4=20 6+20=26 3 22. 09. 2011 a 20*3=60 26+60=86 Схема итерации 12

Другой вариант S (i + 1) = S (i) + a (i + 1); i =0, …, n 1; a (i ) = A(i | m) = m! / (m–i)! a (i + 1) = A(i +1 | m) = m! / (m – i – 1)! S(0) =1; Хотим вычислять a (i + 1) = a (i) * нечто, т. е. нечто = a (i +1) / a (i) = = (m! / (m – i – 1)!) / (m! / (m – i)!) = = (m – i)! / (m – i – 1)! = (m – i) Т. о. a (i + 1) = a (i) * (m – i) 22. 09. 2011 Схема итерации 13

//n 0, S(i)=a(0)+. . . +a(i) , a(i + 1) = a(i) * (m – i) i = 0; a = 1; s = 1; //(a = a(0) = 1) & (s = S(0) = 1) & (i = 0) while ( i < n ) { // (a=a(i)) & (s=S(i)) & (0 i < n) a = a* (m – i); s = s + a; i = i +1; //(a=a(i)) & (s=S(i)) & (0 < i n) } //(a=a(n)) & (s=S(n)) & (0 i = n) 22. 09. 2011 Схема итерации 14

См. пример 2. 4 (с. 14 -16) в учебном пособии и программу sum_1. cpp (демонстрировать на лекции) 22. 09. 2011 Схема итерации 15

С этого места – Лекция 5 (29. 09. 2011)! (т. е. этот материал войдет в след. лекцию) 22. 09. 2011 Схема итерации 16

Пример 4. Последовательность чисел Фибоначчи определяется рекуррентным соотношением F(i + 1) = F(i) + F(i – 1) с начальными условиями F(0) = 0 и F(1) = 1. Требуется вычислить число Фибоначчи F(n) c заданным номером n 1. Вставка про числа Фибоначчи Рекурре нтная после довательность (от лат. recurrens, — возвращающийся), то же, что возвратная последовательность 22. 09. 2011 Схема итерации 17

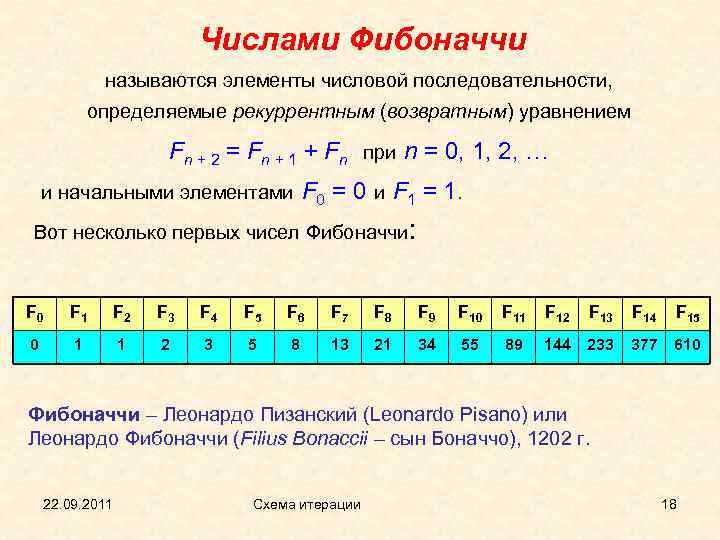Числами Фибоначчи называются элементы числовой последовательности, определяемые рекуррентным (возвратным) уравнением Fn + 2 = Fn + 1 + Fn при n = 0, 1, 2, … и начальными элементами F 0 = 0 и F 1 = 1. Вот несколько первых чисел Фибоначчи: F 0 F 1 F 2 F 3 F 4 F 5 F 6 F 7 F 8 F 9 F 10 F 11 F 12 F 13 F 14 F 15 0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 Фибоначчи – Леонардо Пизанский (Leonardo Pisano) или Леонардо Фибоначчи (Filius Bonaccii – сын Боначчо), 1202 г. 22. 09. 2011 Схема итерации 18

Утверждение: где и есть корни квадратного уравнения и Число 1. 61803… называют «золотым сечением» Конец вставки 22. 09. 2011 Схема итерации 19

Пример 4. Последовательность чисел Фибоначчи определяется рекуррентным соотношением F(i + 1) = F(i) + F(i – 1) с начальными условиями F(0) = 0 и F(1) = 1. Требуется вычислить число Фибоначчи F(n) c заданным номером n 1. Указание: использовать только рекуррентное соотношение и операции с целыми числами. Замечание о форме рекуррентного соотношения: F(i + 1) = F(i) + F(i – 1), i = 1, 2, …; F(0) = 0 и F(1) = 1. при n = 2, 3, 4, …; F = 0 и F = 1. Fn + 2 = Fn + 1 + Fn при n = 0, 1, 2, …; F 0 = 0 и F 1 = 1. Fn = Fn - 1 + Fn - 2 22. 09. 2011 Схема итерации 0 1 20

Вычисление числа Фибоначчи F(n) c заданным номером n 1 Поскольку при вычислении F(i + 1) используется пара F(i) и F(i – 1), то в программе будем использовать пару переменных a и b, таких, что после i-й итерации ai = F(i) и bi = F(i – 1). Тогда переход от пары (a i – 1, b i – 1) к паре (ai, bi) есть: ai = a i – 1 + b i – 1 bi = a i – 1 и a 1 = 1, b 1 = 0 22. 09. 2011 Схема итерации 21

Действительно, если a i – 1 = F(i – 1) и b i – 1 = F(i – 2), то по (**) будут вычислены ai = F(i – 1) + F(i – 2) = F(i) и bi = F(i – 1). Начальная установка обеспечивает a 1 = F(1) и b 1 = F(0). Эти рекуррентные вычисления с переменными var a, b, c, i, n: Integer реализуются следующим фрагментом программы (при n 1) 22. 09. 2011 Схема итерации 22

a : = 1; b : = 0; i : = 1; {У 1: (a=F(1)) & (b=F(0)) } while (i < n) do begin {У 2: (a=F(i)) & (b=F(i-1)) & (1 i

Пример 5. Модификация примера 4. Известно, что значения стандартного целого типа Integer в языке Паскаль имеют верхнюю границу Max. Int (предопределенная константа, равная 32767). Требуется вычислить число Фибоначчи F(n), максимальное среди целых чисел типа Integer, и его номер n. 1. n = max {n N | F(n) ≤ Max. Int}; 2. n = min {n N | F(n + 1) > Max. Int}; 3. такое n, что (F(n) ≤ Max. Int) & (F(n + 1) > Max. Int). Max. Int 22. 09. 2011 F(n) Схема итерации F(n+1) 24

На i-м шаге должно быть вычислено следующее число Фибоначчи: F(i) = a + b = F(i – 1) + F(i – 2). Непосредственно проверить неравенство a + b Max. Int нельзя ! (a + b Max. Int) (a Max. Int – b) Условие продолжения цикла (a Max. Int – b) 22. 09. 2011 Схема итерации 25

Модификация примера 4 в 5 a : = 1; b : = 0; i : = 1; {a=F(1) & b=F(0)} while (a Max. Int – b ) do begin {(a=F(i)) & (b=F(i-1)) & (a+b Max. Int)} i : = i + 1; c : = a; a : = a + b; b : = c {(a=F(i)) & (b=F(i-1)) & (a Max. Int)} end; {(a=F(i)) & (b=F(i-1)) & (a Max. Int) & (a+b>Max. Int) & (n=i)} 22. 09. 2011 Схема итерации 26

Пример 6. Требуется вычислить по заданному натуральному n 1 число Фибоначчи F(n). Если число F(n) выходит за диапазон стандартных целых чисел (F(n) > Max. Int), то вычислить максимальное F(i), как в прим. 5 (i < n). Условие продолжения B цикла while-do следует взять как конъюнкцию (&) условий продолжения из примеров 4 и 5: B (i < n) & (a (Max. Int – b)) Условие завершения цикла Not B (i n) or (a > (Max. Int – b)) (a & b) = ( a) ( b) 22. 09. 2011 Схема итерации 27

См. программу в учебном пособии «РКП (Практикум)» на стр. 13 -14 a : = 1; b : = 0; i : =1; {a=F(1) & b=F(0)} while (i < n) and (a <= (Max. Int - b)) do begin { (a=F(i)) & (b=F(i-1)) & (a+b=F(i+1)<=Max. Int) &(1<=iMax. Int))} (i n) с учетом i : = i + 1 22. 09. 2011 Схема итерации 28

КОНЕЦ ЛЕКЦИИ КОНЕЦ ЛЕКЦИИ 22. 09. 2011 Схема итерации 29