Programming and Using ECLi PSe Execution Basics

Programming and Using ECLi. PSe

Execution Basics ¡ ¡ Execution can be regarded as a search through a tree-shaped search-space. Attempts to find solution(s) to query, given the program (rules, facts, constraints) 3

Basic Syntax ¡ Terms are basic “building blocks”. Can be: l l variables l structures l ¡ atomic list (specialised structure) Terms are used to build programs (facts, rules, constraints are all terms syntactically) 4

Terms: Atomic Types Atomic terms: “constants” ¡ atoms start with lower-case letter, or wrapped in single quotes e. g. atom a 3 ’Atom’ ’an atom’ ¡ ? ? ? strings wrapped in double quotes e. g. "purple" ¡ -*- "a string" "" numbers: integers floats rationals bounded reals e. g. 1 9999 -23 643463461293469 3. 1416 -1. 0 e 5 1. 0 Inf 1_3 22_7 3. 14159__3. 14160 -1. 01__-0. 99 5

Terms: Structures ¡ ¡ Characterised by name and arity (number of arguments) name/arity is called functor Arguments are again arbitrary terms (untyped) Canonical syntax colour(purple) neighbour(france, germany) s(s(s(0))) ¡ Operator syntax Some structures can be written in alternative syntax (if declared) e. g. infix 1 + 2 is exactly the same as +(1, 2) 6

Terms: Lists ¡ Specialised structures, with special syntax e. g. ¡ [1, 2, 3] [] (empty list) List consists of a head and a tail Head is the first element of a list Tail is the rest of the list (also a list) Can be written [Head | Tail] ¡ These are equivalent: [1, 2, 3] [1 | [2, 3]] [1 | [2 | [3 | []]]] 7

Logical Variables ¡ Placeholders for values Free/instantiated ¡ Not memory locations Not mutable, single assignment ¡ Names start with a capital letter e. g. Colour Countries Scope is the term: p(X, X). ¡ q(X). Anonymous variables written as _ Each _ is a different variable! 8

Predicates, Goals and Queries ¡ Built-in/library predicates have predefined meaning e. g. integer(X) is true iff X is an integer ¡ A goal is a formula whose truth we want to know integer(99) integer(hello) ¡ A query is the top-level goal ? - integer(99). Yes. ? - integer(hello). No. 9

Matching ? - 3 = 3. Yes. ? - foo(a, 2) = foo(a, 2, c). No. ? - 3 = 4. No. ? - foo(3, 4) = 7. 13 No. ? - hello = 3. No. ? - foo(a, 2) = foo(a, 2). Yes. ? - +(3, 4) = 7. No. ? - 3 + 4 = 7. No. ? - foo(a, 2) = foo(b, 2). No. 10

Unification = matching after variable substitution ? - X = 3 Yes. ? - X = foo(a, 2) Yes. ? - 3 = X. X = 3 Yes. ? - foo(X, Y) = foo(a, 2). X = a Y = 2 Yes. ? - X = 3, Y = 4. X = 3 Y = 4 Yes. ? - X = 3, X = 4. No. ? - foo(X, 2) = foo(a, Y). X = a Y = 2 Yes. ? - foo(X, X) = foo(a, 2). No. 11

Unification examples ¡ Will these succeed or fail? ? - point(X, Y) = point(A, 1). Yes: X = A, Y = 1 ? - point(X, Y, Z) = point(1, 2). No ? - 1 + 3 = 4. No ? - Apples = Oranges. Yes: Apples = Oranges ? - 'Atom' = "Atom". No 12

Unification with Domain Variables Requires solving simple equality constraints: ? - X: : 1. . 5, Y: : 3. . 7, X = Y. X = X{3. . 5} Yes. ? - X: : 1. . 5, foo(X) = foo(9). No. ? - X: : 1. . 5, Y: : 3. . 7, foo(X, Y) = foo(Z, Z). X = X{3. . 5} Yes. 13

Program = Predicate definitions ¡ Predicate definitions consist of clauses that define what’s true Facts: brother(fred, jane). ‘fullstop’ male(fred). Rules: uncle(Uncle, Nephew) : brother(Uncle, Parent), parent(Parent, Nephew). means: Uncle Nephew Parent brother(Uncle, Parent) parent(Parent, Nephew) ¡ Directives: : - use_module(library(ic)). 14

Conjunction and Disjunction ¡ Conjunction is written as comma: uncle(U, N) : brother(U, P), parent(P, N). ¡ Operational semantics: left-to-right execution ¡ Disjunction either as alternative clauses: atomic_particle(proton). atomic_particle(neutron). atomic_particle(electron). ¡ or explicitly as semicolon: atomic_particle(X) : ( X = proton ; X = neutron ; X = electron ). ¡ Operational semantics: left-to-right try and backtrack 15

Recursion ¡ Defining rule with recursion ancestor(X, Y) : - parent(X, Y). ancestor(X, Y) : parent(Z, Y), ancestor(X, Z). ¡ Tip for programming recursion: assume predicate already defined when writing the recursive case 16

Execution model ¡ Keep a “resolvent” of unsolved subgoals Start with initial query Stop when resolvent empty ¡ Process subgoals from left-to-right Simplify subgoals by applying predicate definitions Accumulate variable substitutions in the process ¡ If a contradiction occurs, backtrack Undo everything since the most recent alternative Try the next alternative left-to-right 17

Basic Execution ? - ancestor(abe, bart). Try clause 1 2 Ancestor 1 = abe, Descendant 1 = bart ? - parent(abe, Child 1), ancestor(Child 1, bart). Try clause 1 Child 1 = homer ? - ancestor(homer, bart). Ancestor 2 = homer, Descendant 2 = bart Try clause 1 ? - parent(homer, bart). Try clause 3 Success! ancestor(Ancestor, Descendant) : parent(Ancestor, Descendant). ancestor(Ancestor, Descendant) : parent(Ancestor, Child), parent(abe, homer). parent(abe, herbert). parent(homer, bart). parent(marge, bart). ancestor(Child, Descendant). 18

If-then-else construct ¡ ( Condition -> Then ; Else ) l l ¡ If Condition succeeds, any choices made in it are committed to and Then is executed If Condition failed, Else is executed Example max(X, Y, Max) : ( X > Y -> Max = X ; Max = Y ). ¡ Use with simple tests only! 19

Some built-ins for list processing ¡ member(Term, List) ¡ length(List, N) ¡ append(List 1, List 2, Appended. List) ¡ reverse(List, Reversed) ¡ sort(List, Sorted) ¡ flatten(Nested. List, Flat. List) ? - flatten([[1, 2, 3], 2, [], [[3], 4], 5], L). L = [1, 2, 3, 4, 5] Yes 20

All solutions predicates: findall/3 ¡ findall(? Term, +Goal, ? List) Finds all solutions of Goal, and creates a list List with an instance of Term for each solution ¡ Example: Given: neighbour(1, 2). neighbour(2, 3). neighbour(3, 1). ? - findall(X-Y, neighbour(X, Y), Neighbours). Neighbours = [1 - 2, 2 - 3, 3 - 1] Yes 22

Libraries ¡ ¡ libraries extends functionality of ECLi. PSe (utilities, solvers…. ) need to be loaded in to ECLi. PSe: : - lib(<Name>) at the start of a program, or lib(<Name>) at top-level prompt ¡ ¡ Can sometimes avoid coding by using libraries check documentations! Interval Constraints library: important solver lib(ic) 25

Programming Issues (I) ¡ Programming = Logic + Control Still programming. Need to think about programming issues ¡ A good specification may not be a good program, e. g. sort(Ls, Ss) : - /* BAD */ permute(Ls, Ss), ordered(Ss). l l Even the constraints version is extremely inefficient - make use of property of problem if available - many sorting algorithms available! In fact, for sorting, should use built-in sorts (efficient as implemented in low level). Often easiest method to find max/min of a list in ECLi. PSe 26

Programming Issues (II) What are the problems with this code? split(Ls, Pivot, Bigs, Smalls) : /* BAD */ findall(L 1, (member(L 1, Ls), L 1 >= Pivot), Bigs), findall(L 2, (member(L 2, Ls), L 2 < Pivot), Smalls). ¡ Misuse of findall/3 - should not use all solutions predicate to traverse list ¡ List traversed twice – redundant computation ¡ Better code: split([], _, []). split([L|Ls], Pivot, Bigs, Smalls) : (L >= Pivot -> Bigs = [L|Bigs 0], Smalls = Smalls 0 ; Bigs = Bigs 0, Smalls = [L|Smalls 0] ), split(Ls, Pivot, Bigs 0, Smalls 0). 28

Generate-and-test ? - coloured([A, B, C, D]). C A B D colour(red). colour(green). coloured([A, B, C, D]) : colour(A), colour(B), colour(C), colour(D), A = B, A = C, A = D, B = C, B = D, C = D. colour(blue). colour(yellow). 29

Extension for Constraint Solving ¡ Some subgoals are viewed as “constraints” Not handled by the general Prolog-mechanism ¡ Either data-driven propagation behaviour Demons delay/resume and propagate information ¡ Or passing to a specialised solver Results get reintegrated ¡ Constrains effectively stay in the resolvent Satisfiability can usually only be decided later ¡ Backtracking mechanism is unaffected Still acts as a “time machine” to reset to an earlier state 30

Constrain-and-search ? - coloured([A, B, C, D]). C A B D colour(red). colour(green). coloured([A, B, C, D]) : A ~= B, A ~= C, A ~= D, B ~= C, B ~= D, C ~= D, colour(A), colour(B), colour(C), colour(D). colour(blue). colour(yellow). 31

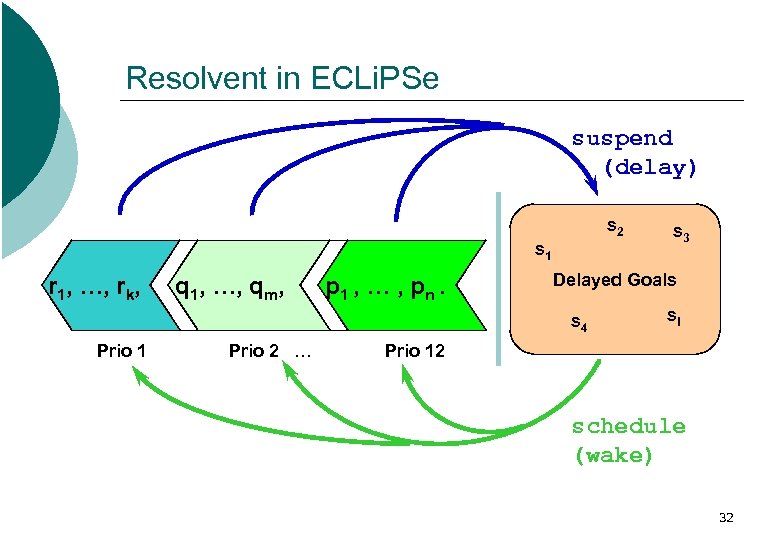
Resolvent in ECLi. PSe suspend (delay) s 2 s 1 r 1, …, rk, q 1, …, qm, p 1 , … , pn. Delayed Goals s 4 Prio 1 Prio 2 … s 3 sl Prio 12 schedule (wake) 32

Overview ¡ ¡ ¡ What is ECLi. PSe? Crash course Logic Programming The Programming Environment 34

Warm-up Exercise ¡ ¡ How to access help How to run a query How to write and compile a program How to use the tracer and inspector 35

ECLi. PSe Documentation ¡ Tutorial Introduction ¡ Application Development Manual ¡ User Manual ¡ Constraint Library Manual ¡ Embedding and Interfacing Manual ¡ Visualisation Tools Manual Html and/or Pdf ¡ Reference Manual Html and plain text (help), details every predicate ¡ Examples Web site 36

Tk. ECLi. PSe ¡ ¡ Development GUI for ECLi. PSe Replaces traditional ‘command line’ interface A toplevel plus a suite of development tools Help available: l l l Popup balloons Help menu for tkeclipse HTML/PDF documentation for all of ECLi. PSe 37

Toplevel ¡ ¡ ¡ Query entry (with history mechanisms) Results window Output window (normal, error, warning, old) Buttons: run, more, make, interrupt Menus: l l File: compilation Run: run query in different modes Tools: development tools Help 38

Compiling Short bits of code: ¡ Tools -> Compile Scratch Pad Larger programs: ¡ Use separate editor to create xxx. ecl file ¡ File -> Compile … ¡ Use make-button to recompile after changes 39

Tracer (debugger) ¡ Call stack: current subgoal + ancestors Right button for popup menu Double click for inspector ¡ ¡ Trace log window Debug command buttons Where to stop after continuing execution ¡ Tools in Menu Print options: change the display of goals/terms Filter: flexible conditional breakpoints Analyze failure: find reason for failure or abort 40

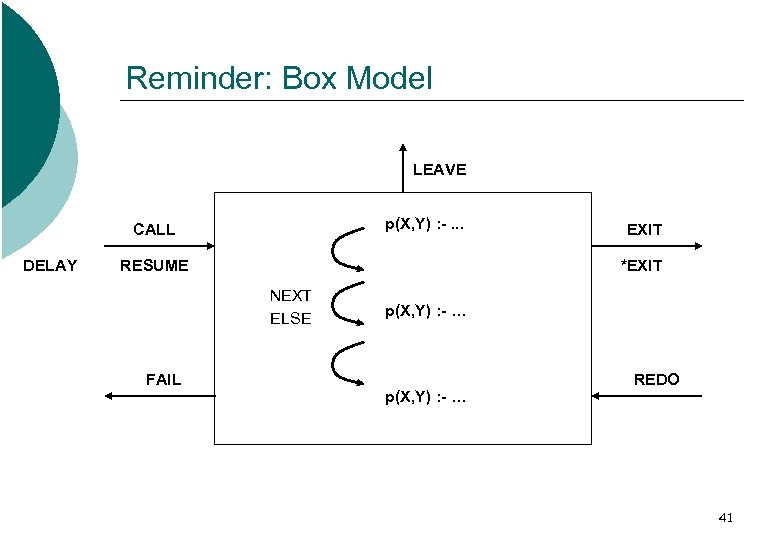
Reminder: Box Model LEAVE p(X, Y) : -. . . CALL DELAY RESUME *EXIT NEXT ELSE FAIL EXIT p(X, Y) : - … REDO 41

Inspector Tree display for structured terms ¡ Double click to expand/collapse term ¡ Right click for popup menu ¡ Useful for debugging 43

Delayed goals viewer ¡ ¡ ¡ Show current suspended goals (unsolved constraints) Woken goals are green Double click to inspect goal with inspector Right click for popup menu on goal Different filter conditions 44

Warm-up Exercise ¡ Write and test a predicate that detects palindromes: ? - palin([k, a, y, a, k]). Yes. ? - palin([a, b, b, a]). Yes. ? - palin([f, o, o]). No. ? - palin(P). P = [] More P = [_203, _203] More … 45