493ab42045007c9ab60edadff28e13b9.ppt
- Количество слайдов: 34

Programmable Logic z Regular logic y Programmable Logic Arrays y Multiplexers/Decoders y ROMs z Field Programmable Gate Arrays “Random Logic” Full Custom Design y Xilinx Vertex CS 150 - Fall 2005 – Lec. #3: Programmable Logic - 1 “Regular Logic” Structured Design

Programmable Logic Arrays (PLAs) z Pre-fabricated building block of many AND/OR gates y Actually NOR or NAND y ”Personalized" by making or breaking connections among gates y Programmable array block diagram for sum of products form • • • inputs AND array product terms OR array outputs • • • CS 150 - Fall 2005 – Lec. #3: Programmable Logic - 2

Enabling Concept z Shared product terms among outputs example: F 0 F 1 F 2 F 3 = = A + A C' B' C' + AB + A input side: personality matrix product term AB B'C AC' B'C' A inputs A B 1 1 – 0 1 – C – 1 0 0 – outputs F 0 F 1 0 0 0 1 1 0 1 = uncomplemented in term 0 = complemented in term – = does not participate F 2 1 0 0 1 0 F 3 0 1 0 0 1 output side: 1 = term connected to output 0 = no connection to output reuse of terms CS 150 - Fall 2005 – Lec. #3: Programmable Logic - 3

Before Programming z All possible connections available before "programming" y In reality, all AND and OR gates are NANDs CS 150 - Fall 2005 – Lec. #3: Programmable Logic - 4
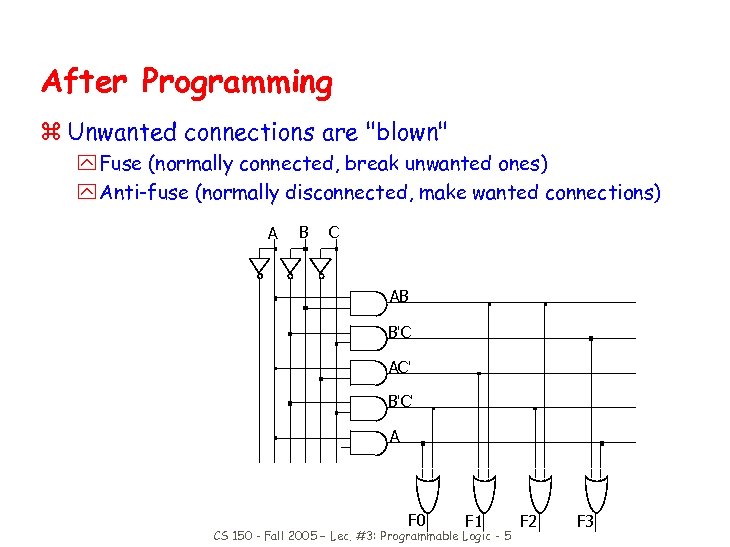
After Programming z Unwanted connections are "blown" y Fuse (normally connected, break unwanted ones) y Anti-fuse (normally disconnected, make wanted connections) A B C AB B'C AC' B'C' A F 0 F 1 CS 150 - Fall 2005 – Lec. #3: Programmable Logic - 5 F 2 F 3
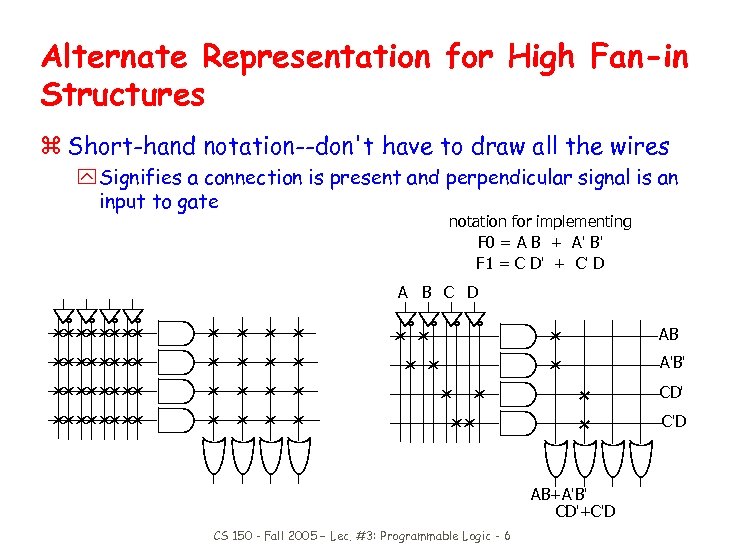
Alternate Representation for High Fan-in Structures z Short-hand notation--don't have to draw all the wires y Signifies a connection is present and perpendicular signal is an input to gate notation for implementing F 0 = A B + A' B' F 1 = C D' + C' D A B C D AB A'B' CD' C'D AB+A'B' CD'+C'D CS 150 - Fall 2005 – Lec. #3: Programmable Logic - 6
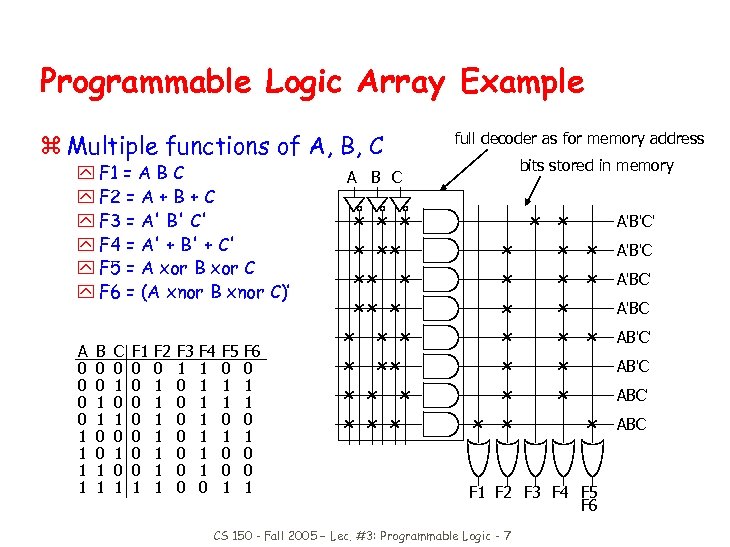
Programmable Logic Array Example z Multiple functions of A, B, C y F 1 = A B C y F 2 = A + B + C y F 3 = A' B' C' y F 4 = A' + B' + C' y F 5 = A xor B xor C y F 6 = (A xnor B xnor C)’ A 0 0 1 1 B 0 0 1 1 C 0 1 0 1 F 1 0 0 0 0 1 F 2 0 1 1 1 1 F 3 1 0 0 0 0 F 4 1 1 1 1 0 F 5 0 1 1 0 0 1 F 6 0 1 1 0 0 1 full decoder as for memory address bits stored in memory A B C A'B'C' A'B'C A'BC' A'BC AB'C' AB'C ABC' ABC F 1 F 2 F 3 F 4 F 5 F 6 CS 150 - Fall 2005 – Lec. #3: Programmable Logic - 7

PLA Design Example z BCD to Gray code converter A 0 0 0 0 1 1 B 0 0 1 1 0 0 0 1 C 0 0 1 1 0 0 1 – D 0 1 0 1 0 1 – – W 0 0 0 1 1 1 – – X 0 0 1 1 0 0 – – Y 0 0 1 1 1 0 0 – – Z 0 1 1 0 – – minimized functions: W=A+BD+BC X = B C' Y=B+C Z = A'B'C'D + B C D + A D' + B' C D' A A 0 1 X 0 X C 0 0 X X X 0 0 X 1 0 1 X 1 C 0 1 X D B B K-map for W D K-map for X A A 0 1 X 0 0 0 X 1 0 1 X 0 1 0 X 0 C 1 1 X X C 0 1 X X 1 0 X X D B B K-map for Y K-map for Z CS 150 - Fall 2005 – Lec. #3: Programmable Logic - 8 D

PLA Design Example (cont’d) z Code converter: programmed PLA A B minimized functions: C D A BD BC BC' B C W=A+BD+BC X = B C' Y=B+C Z = A'B'C'D + B C D + A D' + B' C D' not a particularly good candidate for PLA implementation since no terms are shared among outputs A'B'C'D BCD AD' BCD' W X Y Z however, much more compact and regular implementation when compared with discrete AND and OR gates CS 150 - Fall 2005 – Lec. #3: Programmable Logic - 9
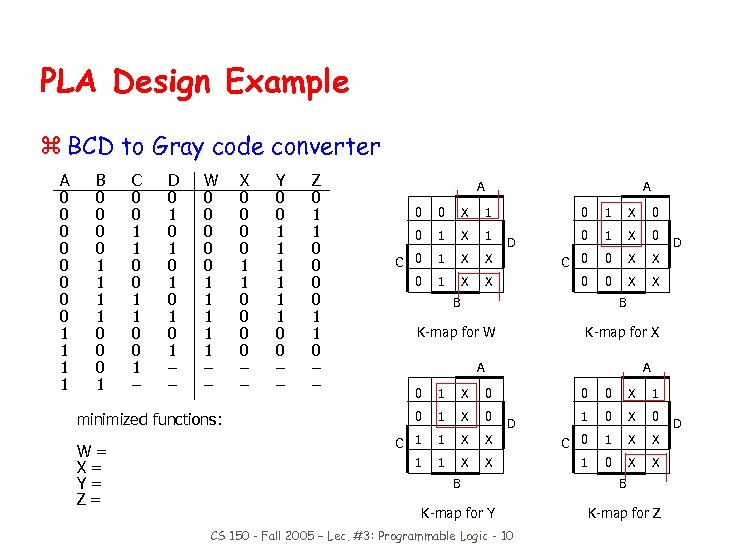
PLA Design Example z BCD to Gray code converter A 0 0 0 0 1 1 B 0 0 1 1 0 0 0 1 C 0 0 1 1 0 0 1 – D 0 1 0 1 0 1 – – W 0 0 0 1 1 1 – – Y 0 0 1 1 1 0 0 – – Z 0 1 1 0 – – A A 0 0 X 1 0 1 X 0 0 1 X 1 0 1 X 0 C 0 1 X X C 0 0 X X 0 1 X X 0 0 X X D B K-map for W D B K-map for X A A 0 1 X 0 C 1 1 X 1 minimized functions: W= X= Y= Z= X 0 0 1 1 0 0 – – 0 0 X 1 1 0 X C 0 1 X X 1 0 X X D B B K-map for Y K-map for Z CS 150 - Fall 2005 – Lec. #3: Programmable Logic - 10 D

PLA Design Example #1 z BCD to Gray code converter A 0 0 0 0 1 1 B 0 0 1 1 0 0 0 1 C 0 0 1 1 0 0 1 – D 0 1 0 1 0 1 – – W 0 0 0 1 1 1 – – Y 0 0 1 1 1 0 0 – – Z 0 1 1 0 – – A A 0 0 X 1 0 1 X 0 0 1 X 1 0 1 X 0 C 0 1 X X C 0 0 X X 0 1 X X 0 0 X X D B K-map for W D B K-map for X BC’ A 0 1 X 0 C 1 1 X 1 minimized functions: W= X= Y= Z= X 0 0 1 1 0 0 – – 1 X A 0 0 X 1 1 0 X C 0 1 X X X 1 0 X X D B B K-map for Y K-map for Z CS 150 - Fall 2005 – Lec. #3: Programmable Logic - 11 D
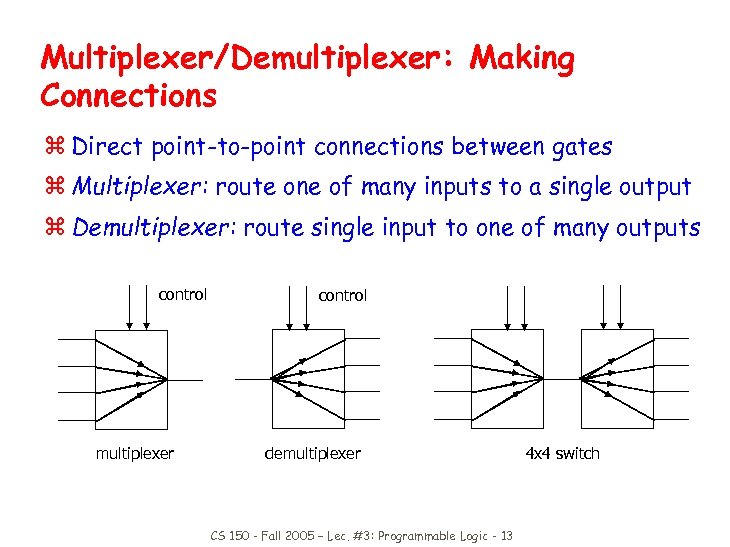
Multiplexer/Demultiplexer: Making Connections z Direct point-to-point connections between gates z Multiplexer: route one of many inputs to a single output z Demultiplexer: route single input to one of many outputs control multiplexer control demultiplexer CS 150 - Fall 2005 – Lec. #3: Programmable Logic - 13 4 x 4 switch

Multiplexers/Selectors z Multiplexers/Selectors: general concept y 2 n data inputs, n control inputs (called "selects"), 1 output y Used to connect 2 n points to a single point y Control signal pattern forms binary index of input connected to output A 0 1 Z = A' I 0 + A I 1 Z I 0 I 1 functional form logical form two alternative forms for a 2: 1 Mux truth table CS 150 - Fall 2005 – Lec. #3: Programmable Logic - 14 I 1 0 0 1 1 I 0 0 0 1 1 A 0 1 0 1 Z 0 0 1 1 1

Multiplexers/Selectors (cont'd) z 2: 1 mux: Z = A' I 0 + A I 1 z 4: 1 mux: Z = A' B' I 0 + A' B I 1 + A B' I 2 + A B I 3 z 8: 1 mux: Z = A'B'C'I 0 + A'B'CI 1 + A'BC'I 2 + A'BCI 3 + AB'C'I 4 + AB'CI 5 + ABC'I 6 + ABCI 7 z In general, Z = 2 n -1 (mk. Ik) y in minterm shorthand form for a 2 n: 1 Mux k=0 I 1 2: 1 mux A Z I 0 I 1 I 2 I 3 4: 1 mux Z A B CS 150 - Fall 2005 – Lec. #3: Programmable Logic - 15 I 0 I 1 I 2 I 3 I 4 I 5 I 6 I 7 8: 1 mux A B C Z
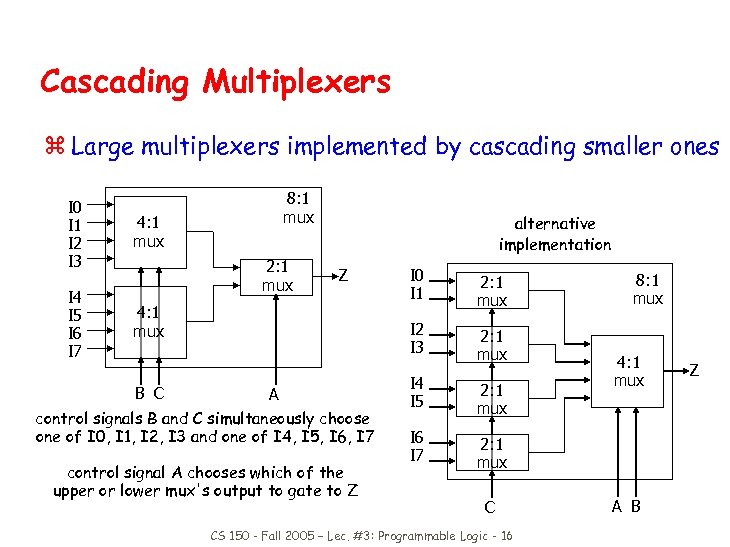
Cascading Multiplexers z Large multiplexers implemented by cascading smaller ones I 0 I 1 I 2 I 3 I 4 I 5 I 6 I 7 8: 1 mux 4: 1 mux 2: 1 mux alternative implementation 4: 1 mux B C A control signals B and C simultaneously choose one of I 0, I 1, I 2, I 3 and one of I 4, I 5, I 6, I 7 control signal A chooses which of the upper or lower mux's output to gate to Z I 0 I 1 2: 1 mux I 2 I 3 Z 2: 1 mux I 4 I 5 2: 1 mux I 6 I 7 8: 1 mux 4: 1 mux 2: 1 mux C CS 150 - Fall 2005 – Lec. #3: Programmable Logic - 16 A B Z

Multiplexers as Lookup Tables (LUTs) z 2 n: 1 multiplexer implements any function of n variables y With the variables used as control inputs and y Data inputs tied to 0 or 1 y In essence, a lookup table z Example: y F(A, B, C) = m 0 + m 2 + m 6 + m 7 = A'B'C' + A'BC' + ABC = A'B'(C') + A'B(C') + AB'(0) + AB(1) CS 150 - Fall 2005 – Lec. #3: Programmable Logic - 17 1 0 0 0 1 1 0 1 2 3 4 8: 1 MUX 5 6 7 S 2 S 1 S 0 A B C F

Multiplexers as LUTs (cont’d) z 2 n-1: 1 mux can implement any function of n variables y With n-1 variables used as control inputs and y Data inputs tied to the last variable or its complement z Example: y F(A, B, C) = m 0 + m 2 + m 6 + m 7 = A'B'C' + A'BC' + ABC = A'B'(C') + A'B(C') + AB'(0) + AB(1) 1 0 0 0 1 1 0 1 2 3 4 8: 1 MUX 5 6 7 S 2 S 1 S 0 A B C F A 0 0 1 1 B 0 0 1 1 C 0 1 0 1 F 1 0 0 0 1 1 C' C' 0 1 CS 150 - Fall 2005 – Lec. #3: Programmable Logic - 18 C' C' 0 1 4: 1 MUX 2 3 S 1 S 0 A B F

Multiplexers as LUTs (cont’d) z Generalization I 0 . . . 0 0 0 1 1 . . 1 0 1 0 single mux data variable . . . In-1 In . n-1 mux control variables I 1 F I I' 1 four possible configurations of truth table rows can be expressed as a function of In n z Example: F(A, B, C, D) implemented by ann 8: 1 MUX A 1 1 C 1 0 0 0 1 0 1 1 choose A, B, C as control variables D multiplexer implementation 0 B CS 150 - Fall 2005 – Lec. #3: Programmable Logic - 19 1 D 0 1 D’ D’ 0 1 2 3 4 8: 1 MUX 5 6 7 S 2 S 1 S 0 A B C

Announcements z We took everyone on the wait list into the class y Result is that Tu labs are very crowded! y Th night lab is very light -- think of switching to get more TA face time! y Send email to pokai@berkeley. edu to request a lab change z First HW due Friday at 2 PM … just before Lab Lecture y CS 150 hand-in box outside and just to the right of 125 Cory doors z Second HW on class web site z Use ucb. class. cs 150 newsgroup for lab, hw, course questions! CS 150 - Fall 2005 – Lec. #3: Programmable Logic - 20
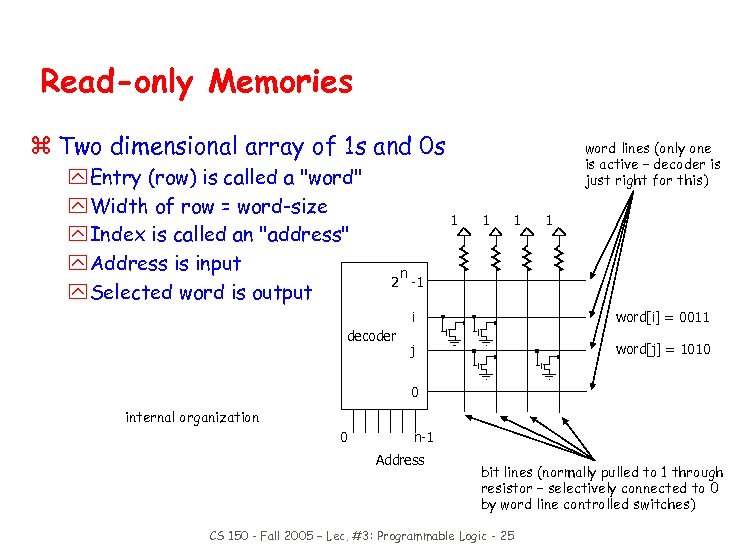
Read-only Memories z Two dimensional array of 1 s and 0 s y Entry (row) is called a "word" y Width of row = word-size y Index is called an "address" y Address is input y Selected word is output word lines (only one is active – decoder is just right for this) 1 1 n 2 -1 i decoder word[i] = 0011 j word[j] = 1010 0 internal organization 0 n-1 Address bit lines (normally pulled to 1 through resistor – selectively connected to 0 by word line controlled switches) CS 150 - Fall 2005 – Lec. #3: Programmable Logic - 25

ROMs and Combinational Logic z Combinational logic implementation (two-level canonical form) using a ROM F 0 = A' B' C + A B' C' + A B' C F 1 = A' B' C + A' B C' + A B C F 2 = A' B' C' + A' B' C + A B' C' F 3 = A' B C + A B' C' + A B C' A 0 0 1 1 B 0 0 1 1 C 0 1 0 1 F 0 0 1 1 0 0 F 1 0 1 1 0 0 1 F 2 1 1 0 0 0 truth table F 3 0 0 0 1 1 0 ROM 8 words x 4 bits/word A B C F 0 F 1 F 2 F 3 address outputs block diagram CS 150 - Fall 2005 – Lec. #3: Programmable Logic - 26

ROM Structure z Similar to a PLA structure but with a fully decoded AND array y Completely flexible OR array (unlike PAL) n address lines • • • inputs decoder 2 n word lines memory array (2 n words by m bits) outputs • • • m data lines CS 150 - Fall 2005 – Lec. #3: Programmable Logic - 27
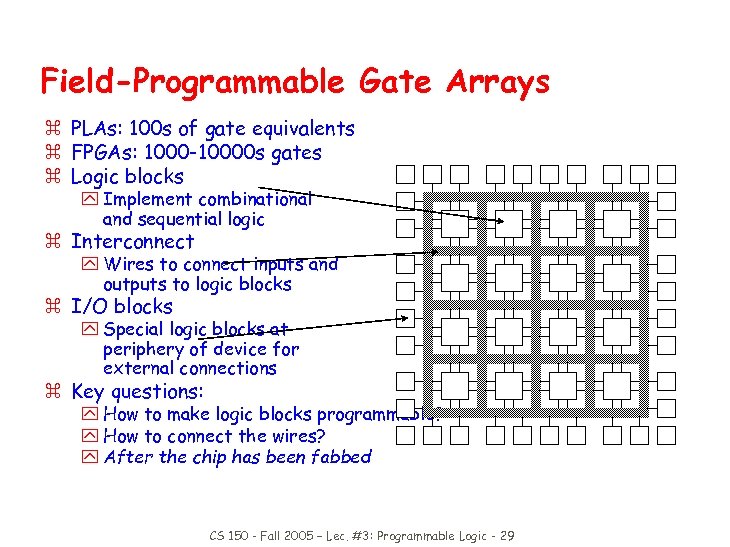
Field-Programmable Gate Arrays z PLAs: 100 s of gate equivalents z FPGAs: 1000 -10000 s gates z Logic blocks y Implement combinational and sequential logic z Interconnect y Wires to connect inputs and outputs to logic blocks z I/O blocks y Special logic blocks at periphery of device for external connections z Key questions: y How to make logic blocks programmable? y How to connect the wires? y After the chip has been fabbed CS 150 - Fall 2005 – Lec. #3: Programmable Logic - 29

Tradeoffs in FPGAs z Logic block - how are functions implemented: fixed functions (manipulate inputs) or programmable? y Support complex functions, need fewer blocks, but they are bigger so less of them on chip y Support simple functions, need more blocks, but they are smaller so more of them on chip z Interconnect y How are logic blocks arranged? y How many wires will be needed between them? y Are wires evenly distributed across chip? y Programmability slows wires down – are some wires specialized to long distances? y How many inputs/outputs must be routed to/from each logic block? y What utilization are we willing to accept? 50%? 20%? 90%? CS 150 - Fall 2005 – Lec. #3: Programmable Logic - 30

Xilinx 4000 Series Programmable Gate Arrays z CLB - Configurable Logic Block y 5 -input, 1 output function y or 2 4 -input, 1 output functions y optional register on outputs z Built-in fast carry logic z Can be used as memory z Three types of routing y direct y general-purpose y long lines of various lengths z RAM-programmable y can be reconfigured CS 150 - Fall 2005 – Lec. #3: Programmable Logic - 31
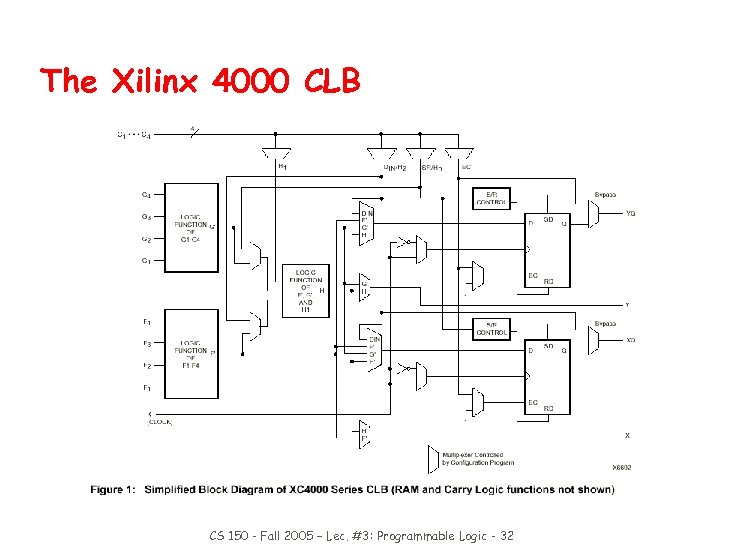
The Xilinx 4000 CLB CS 150 - Fall 2005 – Lec. #3: Programmable Logic - 32
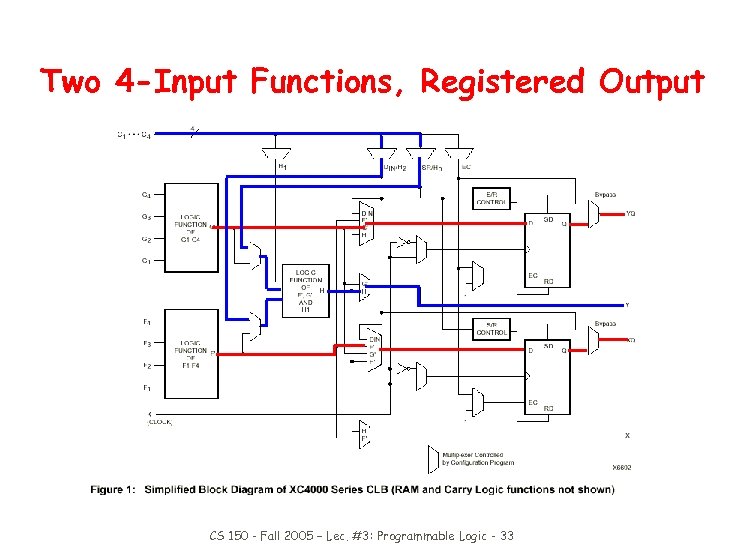
Two 4 -Input Functions, Registered Output CS 150 - Fall 2005 – Lec. #3: Programmable Logic - 33
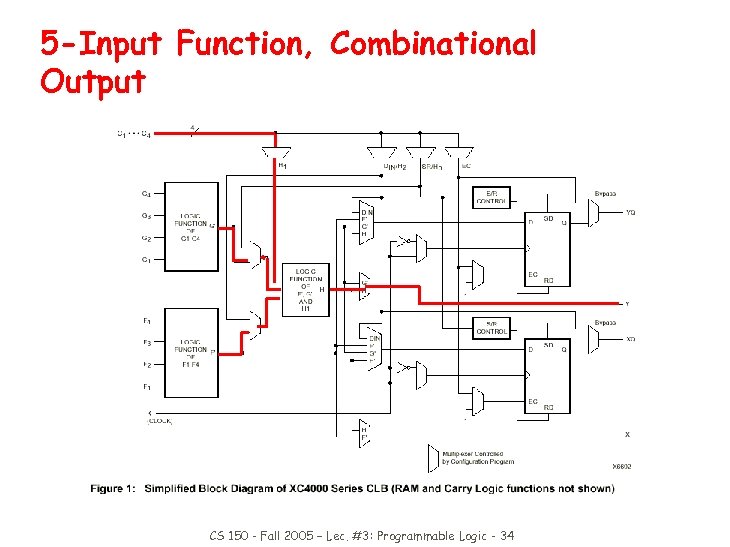
5 -Input Function, Combinational Output CS 150 - Fall 2005 – Lec. #3: Programmable Logic - 34
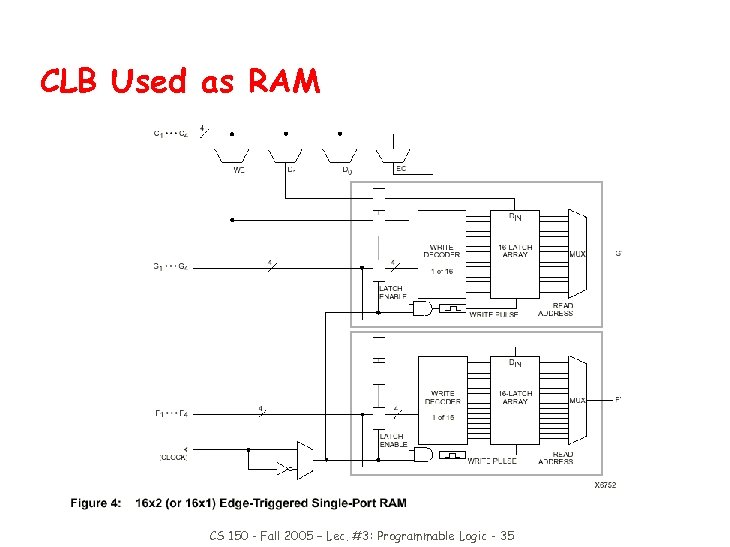
CLB Used as RAM CS 150 - Fall 2005 – Lec. #3: Programmable Logic - 35
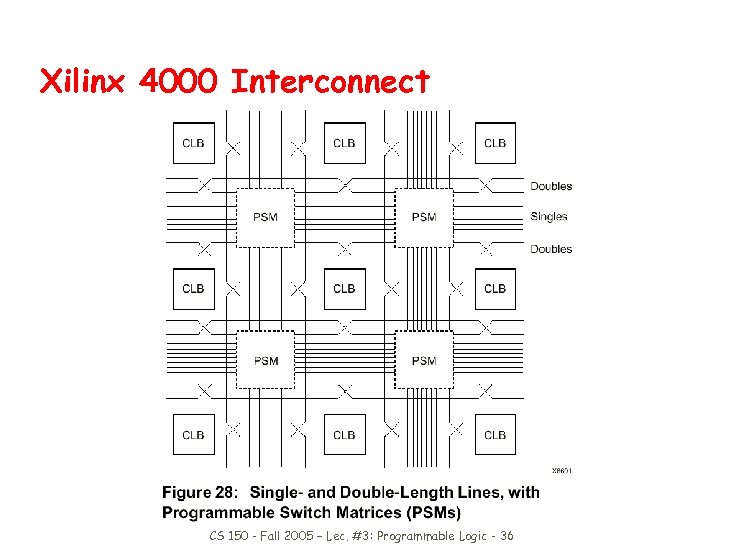
Xilinx 4000 Interconnect CS 150 - Fall 2005 – Lec. #3: Programmable Logic - 36

Xilinx FPGA Combinational Logic Examples z Key: General functions are limited to 5 inputs y (4 even better - 1/2 CLB) y No limitation on function complexity z Example y 2 -bit comparator: A B = C D and A B > C D implemented with 1 CLB (GT) F = A C' + A B D' + B C' D' (EQ) G = A'B'C'D'+ A'B C'D + A B'C D'+ A B C D z Can implement some functions of > 5 input CS 150 - Fall 2005 – Lec. #3: Programmable Logic - 37
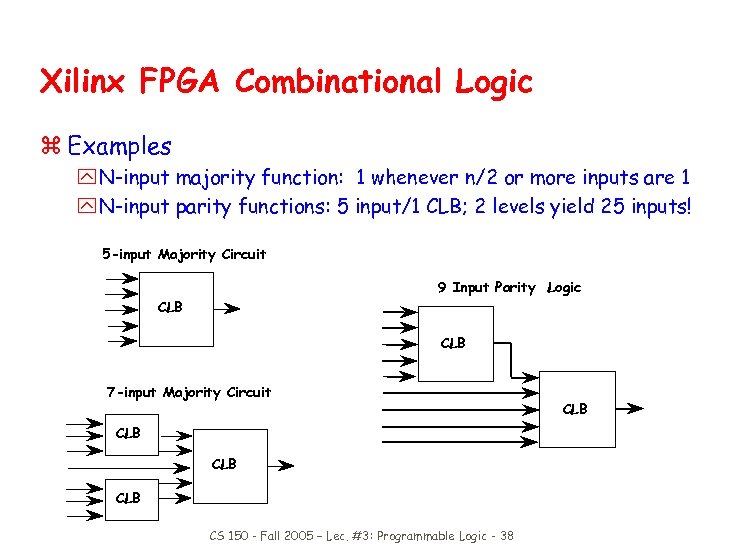
Xilinx FPGA Combinational Logic z Examples y N-input majority function: 1 whenever n/2 or more inputs are 1 y N-input parity functions: 5 input/1 CLB; 2 levels yield 25 inputs! 5 -input Majority Circuit 9 Input Parity Logic CLB 7 -input Majority Circuit CLB CLB CS 150 - Fall 2005 – Lec. #3: Programmable Logic - 38 CLB

Xilinx FPGA Adder Example z Example y 2 -bit binary adder - inputs: A 1, A 0, B 1, B 0, CIN outputs: S 0, S 1, Cout Full Adder, 4 CLB delays to final carry out 2 x Two-bit Adders (3 CLBs each) yields 2 CLBs to final carry out CS 150 - Fall 2005 – Lec. #3: Programmable Logic - 39

Combinational Logic Implementation Summary z Regular Logic Structures y Programmable Logic Arrays x. Programmable connections: AND-OR (NOR-NOR) Arrays y Multiplexers/decoders x. Multipoint connections for signal routing x. Lookup Tables y ROMs x. Truth table in hardware y Field Programmable Gate Arrays (FPGAs) x. Programmable logic (LUTs, Truth Tables) and connections y Advantages/disadvantages of each CS 150 - Fall 2005 – Lec. #3: Programmable Logic - 40
493ab42045007c9ab60edadff28e13b9.ppt