987f47b64cf7fd2b0f5a71054a314703.ppt
- Количество слайдов: 18

Programmable Logic Arrays, Test Review Today: • First Hour: Programmable Logic Arrays – Section 4. 1 of Katz’s Textbook – In-class Activity #1 • Second Hour: Test #1 Q&A, Review. 1
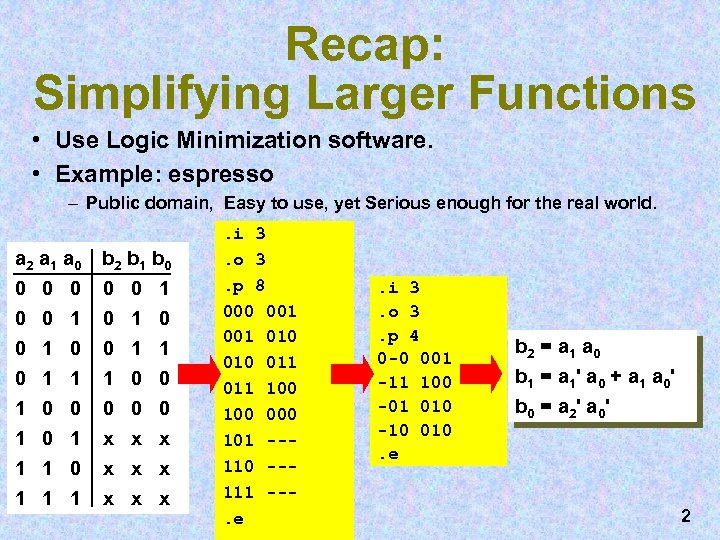
Recap: Simplifying Larger Functions • Use Logic Minimization software. • Example: espresso – Public domain, Easy to use, yet Serious enough for the real world. a 2 a 1 a 0 0 b 2 b 1 b 0 0 0 1 1 1 0 0 1 0 x x 0 1 1 0 1 0 1 1 1 0 0 x x 0 1 0 0 x x x . i 3. o 3. p 8 000 001 010 011 100 000 101 --110 --111 --. e . i 3. o 3. p 4 0 -0 001 -11 100 -01 010 -10 010. e b 2 = a 1 a 0 b 1 = a 1 ' a 0 + a 1 a 0 ' b 0 = a 2 ' a 0 ' 2

Implementing Larger Circuits: Programmable Logic Arrays Old technology: Buy chips with gates (e. g. , a chip with 4 NAND gates), and wire them up to build logic circuits messy wiring, error prone takes lots of space and power Newer technology: Buy a single programmable logic array (PLA) chip Customize this chip to implement our function Can be as easy as downloading an espresso output to a “PLA programmer. ” 3

PLA Example Need to implement the following 3 -input, 4 -output function: F 0 = A + B' C' F 1 = A C' + A B F 2 = B' C' + A B F 3 = B' C + A 4
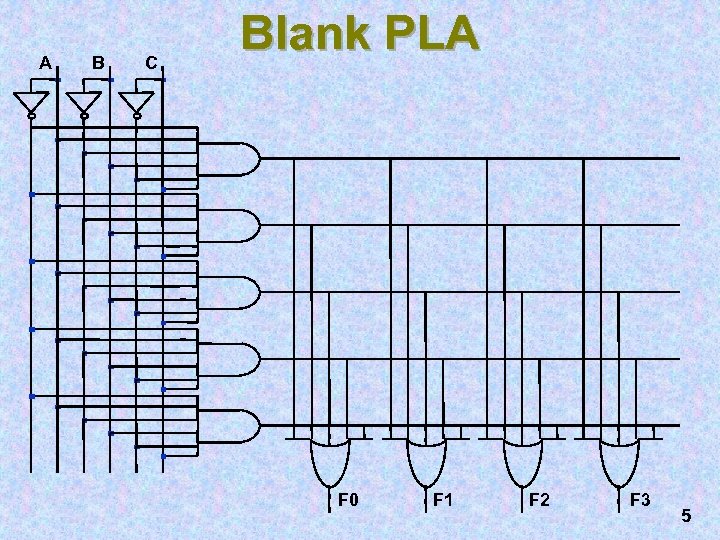
A B C Blank PLA F 0 F 1 F 2 F 3 5
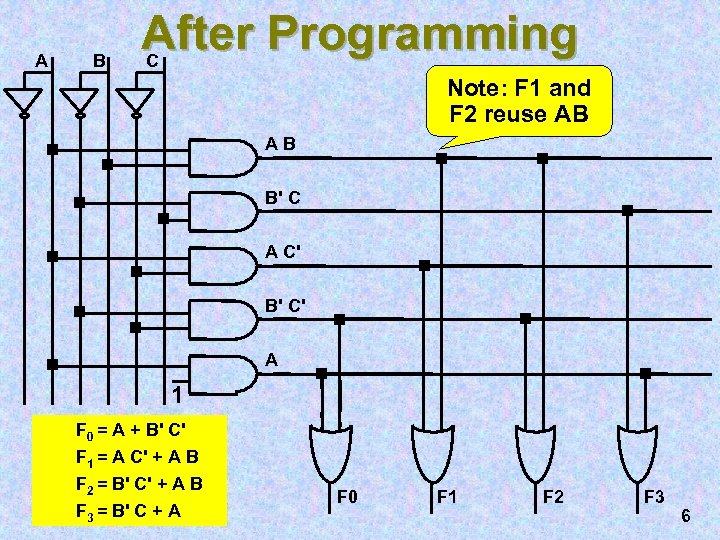
A B After Programming C Note: F 1 and F 2 reuse AB AB B' C A C' B' C' A 1 F 0 = A + B' C' F 1 = A C' + A B F 2 = B' C' + A B F 3 = B' C + A F 0 F 1 F 2 F 3 6

Key to Efficiency: Reuse Shared Terms F 0 = A + B' C' F 1 = A C' + A B F 2 = B' C' + A B F 3 = B' C + A 7

“Personality Matrix” Product term AB B' C A C' B' C' A Inputs Outputs A B C F 0 F 1 F 2 1 1 - 01 0 0 0 1 - 0 0 1 0 - 00 1 1 - - 1 0 0 F 3 0 1 Reuse of 0 0 terms 1 8

How Programming Works • Fuse on each gate input • Blow the fuse with a large current - disconnect that input • Use SW to do this. (Blowing the wrong fuse would be annoying. ) • Other technologies are also used in PLAs, besides fuses. 9
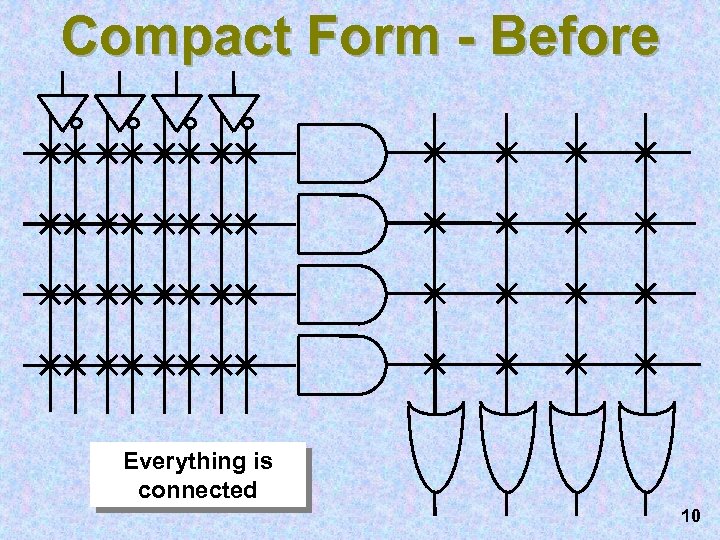
Compact Form - Before Everything is connected 10
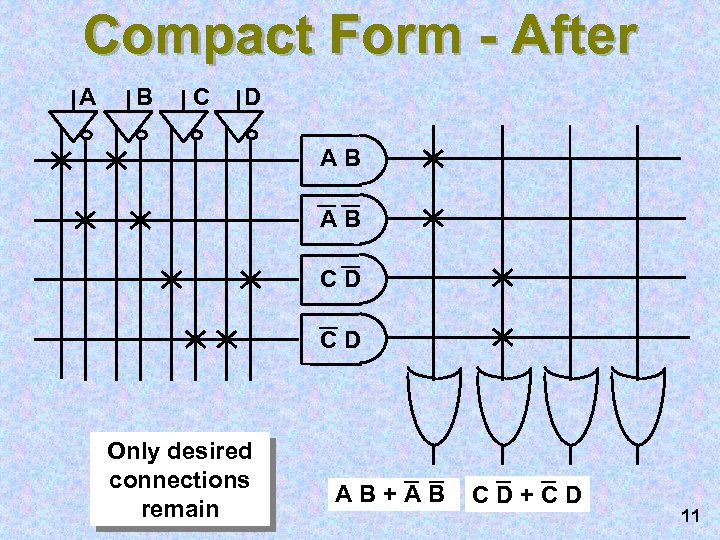
Compact Form - After A B C D AB AB CD CD Only desired connections remain AB+AB CD+CD 11

PAL Programmable array logic • Minor variant on the PLA. – Each output function is OR of a fixed number of terms, say 4. – Does not exploit shared product terms. • E. g. , 16 x 48 x 8 PAL: – 16 inputs (and their complements). – 48 terms ANDing those inputs (or complements) AND – (Note: 48 << 216). – 8 output functions ORing those terms OR • If these restrictions are OK, then the PAL may be cheaper. 12
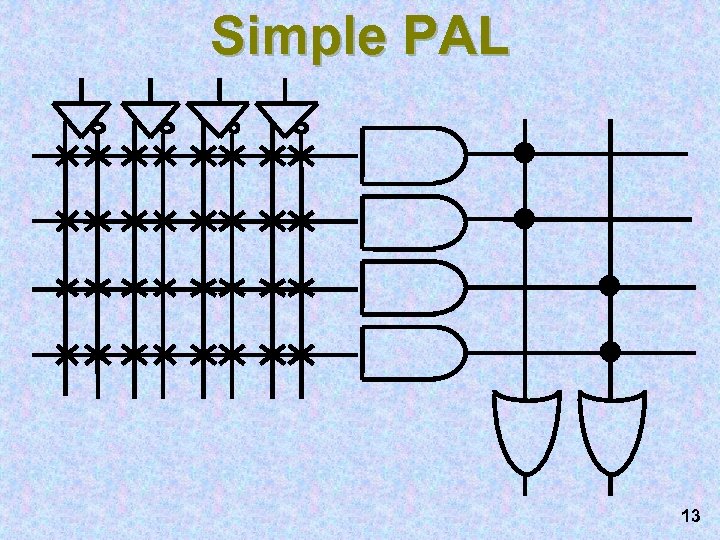
Simple PAL 13

Ex: BCD to Gray Code A 0 0 0 0 1 1 1 1 B 0 0 0 0 1 1 1 1 C 0 0 1 1 D 0 1 0 1 W 0 0 0 1 1 1 X X X X 0 0 1 1 0 0 X X X Y 0 0 1 1 1 0 0 X X X Z 0 1 1 0 X X X Nonstandard Gray Code sequence 14
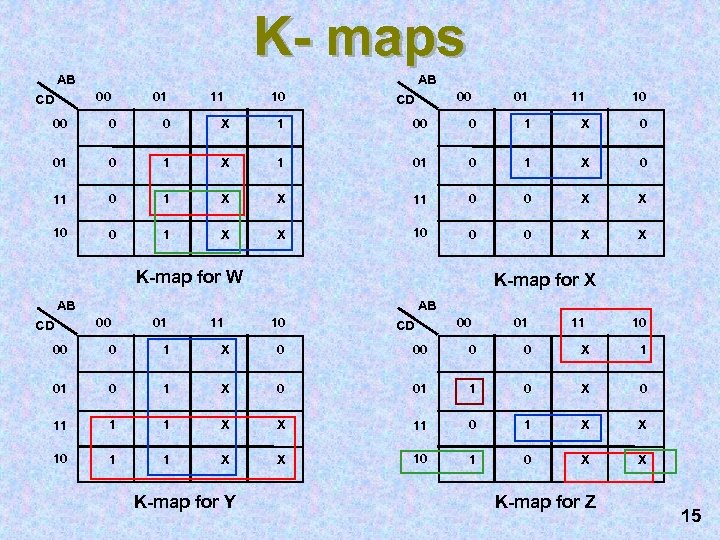
K- maps AB AB 00 CD 01 11 10 00 0 0 X 1 00 0 1 X 0 01 0 1 X 1 01 0 1 X 0 11 0 1 X X 11 0 0 X X 10 0 1 X X 10 0 0 X X K-map for W K-map for X AB CD AB 00 01 11 10 CD 00 01 11 10 00 0 1 X 0 00 0 0 X 1 01 0 1 X 0 01 1 0 X 0 11 1 1 X X 11 0 1 X X 10 1 0 X X K-map for Y K-map for Z 15

Minimized Functions W=A+BD+BC X = B C' Y=B+C Z = A' B' C' D + B C D + A D' + B' C D’ • No shared terms 16
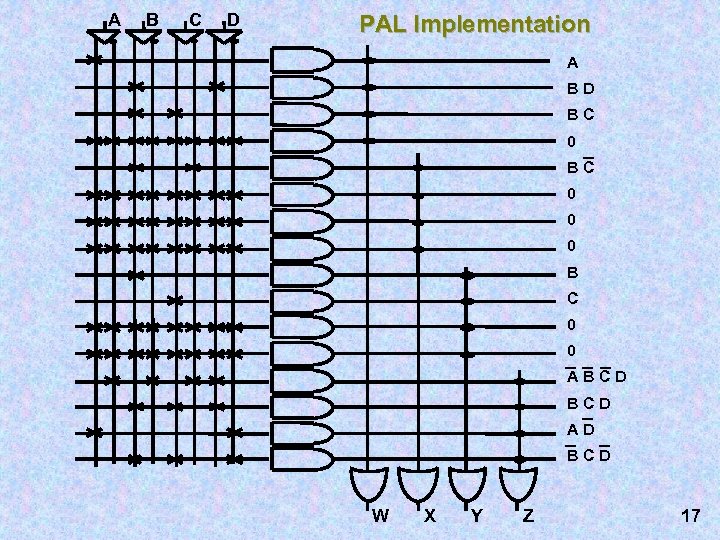
A B C D PAL Implementation A BD BC 0 0 0 B C 0 0 ABCD AD BCD W X Y Z 17

Do Activity #1 Now Due: End of Class Today RETAIN THE LAST PAGE (#3)!! For Next Class: • Bring Randy Katz Textbook • Required Reading: – Sec 4. 1, 4. 2 of Katz • This reading is necessary for getting points in the Studio Activity! 18
987f47b64cf7fd2b0f5a71054a314703.ppt