ПРОГРАММА КУРСА Ø Методы решения нелинейных уравнений Ø

ПРОГРАММА КУРСА Ø Методы решения нелинейных уравнений. Ø Решение системы линейных уравнений. Ø Вычисление определенного интеграла. Оценка погрешности методов. Ø Интерполирование. Ø Аппроксимация.

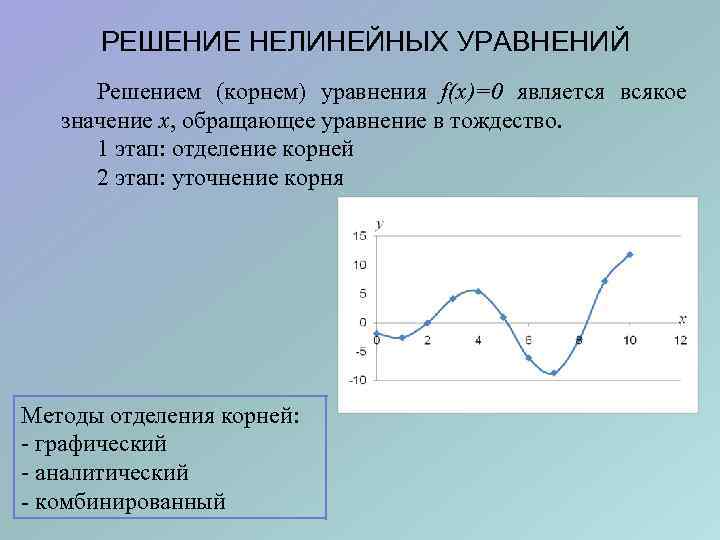РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ Решением (корнем) уравнения f(x)=0 является всякое значение x, обращающее уравнение в тождество. 1 этап: отделение корней 2 этап: уточнение корня Методы отделения корней: - графический - аналитический - комбинированный

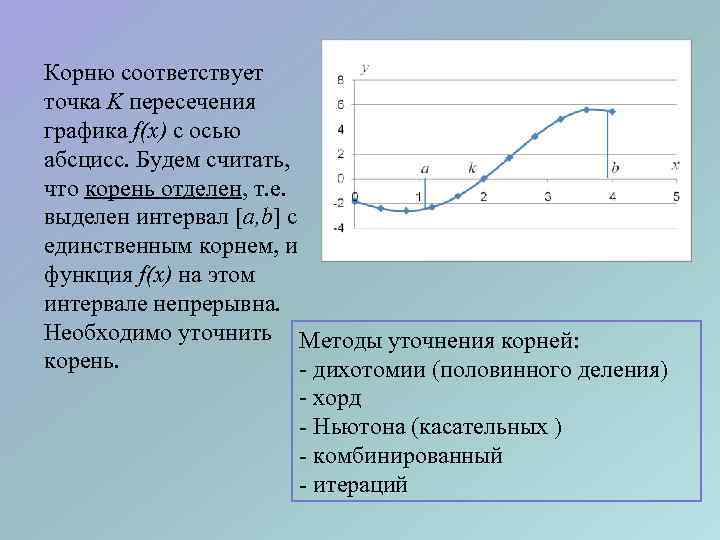Корню соответствует точка K пересечения графика f(x) с осью абсцисс. Будем считать, что корень отделен, т. е. выделен интервал a, b с единственным корнем, и функция f(x) на этом интервале непрерывна. Необходимо уточнить Методы уточнения корней: корень. - дихотомии (половинного деления) - хорд - Ньютона (касательных ) - комбинированный - итераций

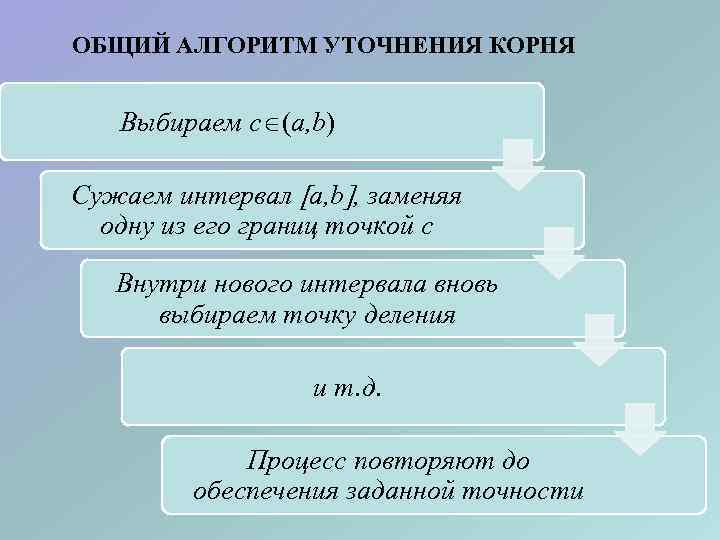ОБЩИЙ АЛГОРИТМ УТОЧНЕНИЯ КОРНЯ Выбираем c (a, b) Сужаем интервал a, b , заменяя одну из его границ точкой c Внутри нового интервала вновь выбираем точку деления и т. д. Процесс повторяют до обеспечения заданной точности

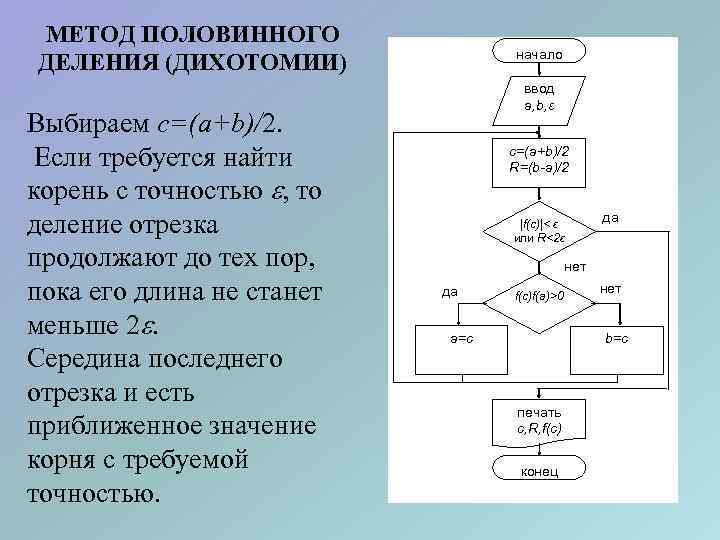МЕТОД ПОЛОВИННОГО ДЕЛЕНИЯ (ДИХОТОМИИ) Выбираем c=(a+b)/2. Если требуется найти корень с точностью , то деление отрезка продолжают до тех пор, пока его длина не станет меньше 2. Середина последнего отрезка и есть приближенное значение корня с требуемой точностью. начало ввод a, b, ε c=(a+b)/2 R=(b-a)/2 |f(c)|< ε или R<2ε да нет да f(c)f(a)>0 a=c нет b=c печать c, R, f(c) конец

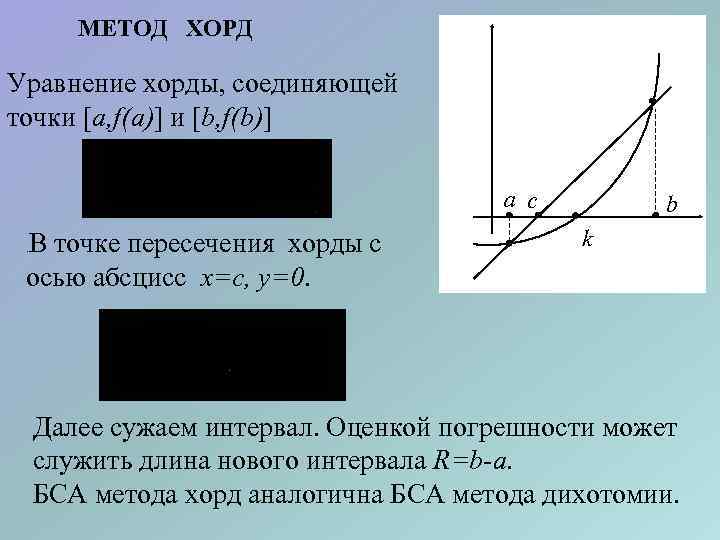МЕТОД ХОРД Уравнение хорды, соединяющей точки a, f(a) и b, f(b) a c В точке пересечения хорды с осью абсцисс x=c, y=0. . b k Далее сужаем интервал. Оценкой погрешности может служить длина нового интервала R=b-a. БСА метода хорд аналогична БСА метода дихотомии.

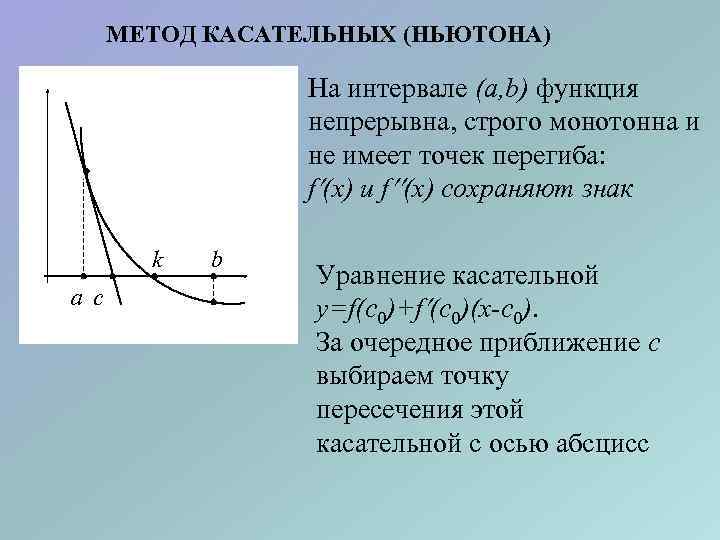МЕТОД КАСАТЕЛЬНЫХ (НЬЮТОНА) На интервале (a, b) функция непрерывна, строго монотонна и не имеет точек перегиба: f (x) и f (x) сохраняют знак k a c b Уравнение касательной y=f(c 0)+f (c 0)(x-c 0). За очередное приближение c выбираем точку пересечения этой касательной с осью абсцисс

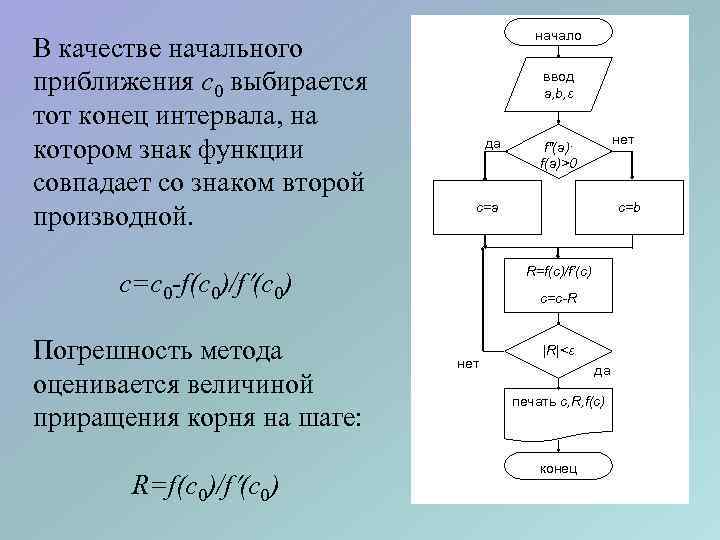В качестве начального приближения c 0 выбирается тот конец интервала, на котором знак функции совпадает со знаком второй производной. начало ввод a, b, ε да c=a c=c 0 -f(c 0)/f (c 0) Погрешность метода оценивается величиной приращения корня на шаге: R=f(c 0)/f (c 0) нет f″(a)∙ f(a)>0 c=b R=f(c)/f’(c) c=c-R нет |R|<ε да печать c, R, f(c) конец

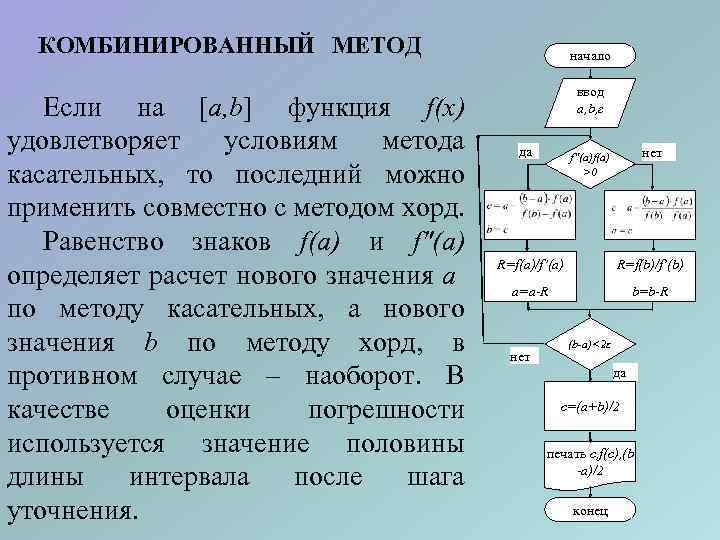КОМБИНИРОВАННЫЙ МЕТОД Если на a, b функция f(x) удовлетворяет условиям метода касательных, то последний можно применить совместно с методом хорд. Равенство знаков f(a) и f″(a) определяет расчет нового значения a по методу касательных, а нового значения b по методу хорд, в противном случае – наоборот. В качестве оценки погрешности используется значение половины длины интервала после шага уточнения. начало ввод a, b, ε да нет f″(a)f(a) >0 R=f(a)/f’(a) R=f(b)/f’(b) a=a-R b=b-R нет (b-a)<2ε да c=(a+b)/2 печать c, f(c), (b -a)/2 конец

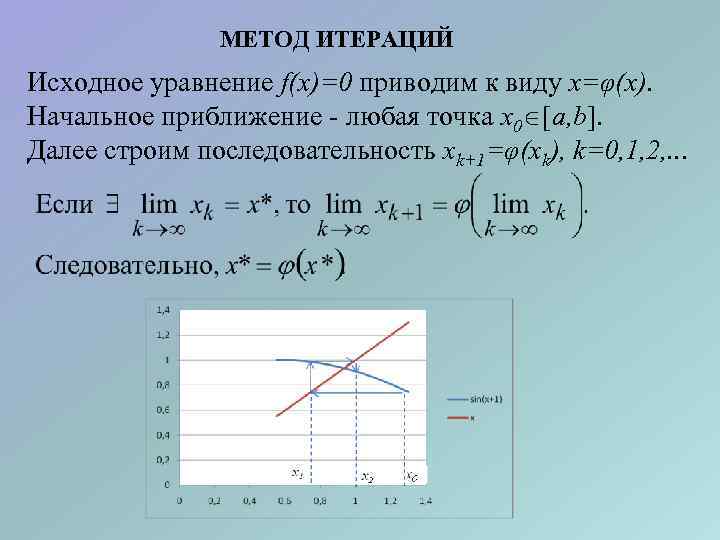МЕТОД ИТЕРАЦИЙ Исходное уравнение f(x)=0 приводим к виду x=φ(x). Начальное приближение - любая точка x 0 a, b. Далее строим последовательность xk+1=φ(xk), k=0, 1, 2, . . .

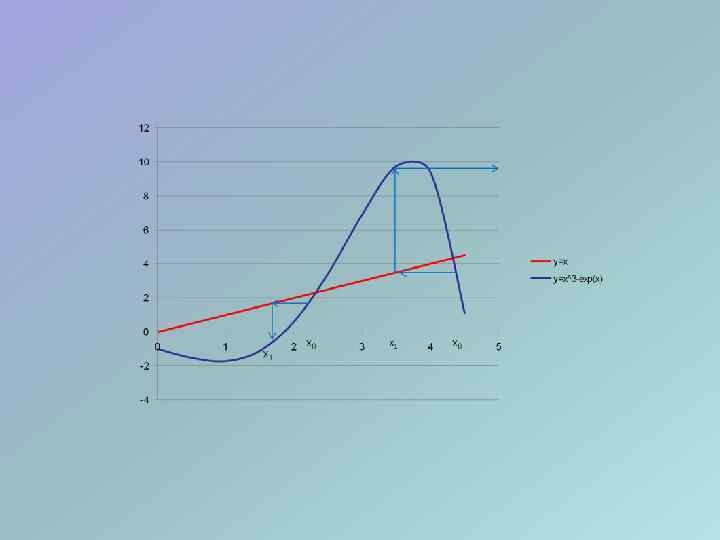
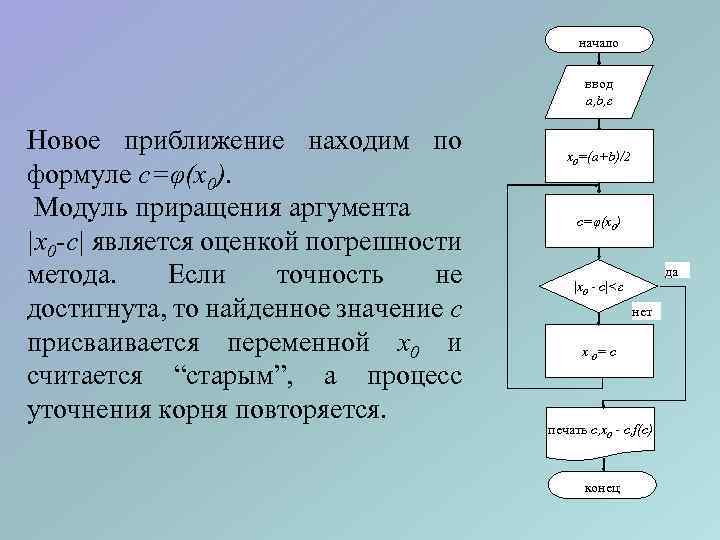начало ввод a, b, ε Новое приближение находим по формуле c=φ(x 0). Модуль приращения аргумента |x 0 -c| является оценкой погрешности метода. Если точность не достигнута, то найденное значение c присваивается переменной x 0 и считается “старым”, а процесс уточнения корня повторяется. x 0=(a+b)/2 c=φ(x 0) да |x 0 - c|<ε нет x 0= c печать c, x 0 - c, f(c) конец

ЗАМЕЧАНИЯ 1. Для того чтобы процесс сходился, на интервале a, b должно выполняться условие | (x)|<1 2. Трудности перехода от исходного уравнения к уравнению x=φ(x) с выполнением условия сходимости можно преодолеть, если сначала перейти к уравнению x=x-f(x)/k, которое эквивалентно исходному. Здесь k - произвольный параметр, удовлетворяющий на a, b условиям: • |k|>max |f (x)|/2; • знак k совпадает со знаком f (x). Тогда (x)=x-f(x)/k.

ВОПРОСЫ ПО ТЕМЕ 1. Из каких этапов состоит решение нелинейного уравнения? 2. Какие методы отделения корней вы знаете? 3. Какие методы уточнения корня вы знаете? 4. Каким условиям должна удовлетворять функция в случае применения метода Ньютона? 5. Каким условиям должна удовлетворять функция в случае применения метода итераций? 6. Показать варианты графиков функций в случаях сходимости и расходимости метода итераций.