Прогнозирование сезонных процессов Выполнили 14 -гу-7 а

Прогнозирование сезонных процессов Выполнили 14 -гу-7(а)

Сезонные колебания- такие изменения уровня динамического ряда, которые вызываются влияниями времени года.

Общий вид индекса сезонности Isi = yi : yti Отношение исходных (эмпирических) уровней ряда динамики yi, к теоретическим (расчетным) уровням yti, выступающим в качестве базы сравнения

Большинство регулярных составляющих временных рядов принадлежит к двум классам: они : являются либо трендом, либо сезонной составляющей. Тренд представляет собой общую систематическую линейную или нелинейную компоненту, которая может изменяться во времени. Сезонная составляющая - это периодически повторяющаяся компонента

Аддитивная модель временного ряда Yt = Тt + S t + Et где Тt – тренд динамического ряда – регулярная компонента, характеризующая общую тенденцию St – сезонная компонента Et – случайная компонента, образующаяся под влиянием различных причин

Сезонность- неравномерность производственной деятельности в отраслях промышленности, связанных с переработкой сельскохозяйственного сырья, поступление которого зависит от времени года

Прогноз базируется на двух компонентах: Компонента тренда представляет тенденцию временного ряда (базовой линии) к повышению либо к понижению. Компонента сезонности представляет любое резкое повышение, понижение или пик базовой линии, которые происходят с одинаковым промежутком времени.

Сезонная компонента St имеет период Т 0, т. е. St+То = St Т 0 = 12 для месячных данных и Т 0 = 4 для квартальных данных. Величина Т 0 содержится в Т целое число (m) раз, т. е. Т = m Т 0

Мультипликативная модель временного ряда Yt = Тt *St * Et где Тt – тренд динамического ряда – регулярная компонента, характеризующая общую тенденцию St – сезонная компонента Et – случайная компонента, образующаяся под влиянием различных причин

Процесс построения модели включает в себя следующие шаги: 1. Выравнивание исходного ряда методом скользящей средней. 2. Расчет значений сезонной компоненты. 3. Устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных в аддитивной или мультипликативной модели. 4. Аналитическое выравнивание уровней и расчет значений тренда с использованием полученного уравнения тренда. 5. Расчет полученных по модели значений или 6. Расчет абсолютных и относительных ошибок.

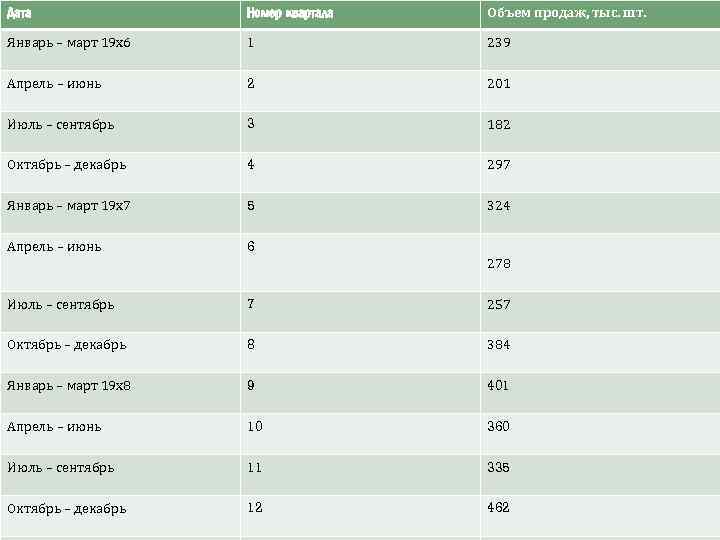Дата Номер квартала Объем продаж, тыс. шт. Январь – март 19 х6 1 239 Апрель – июнь 2 201 Июль – сентябрь 3 182 Октябрь – декабрь 4 297 Январь – март 19 х7 5 324 Апрель – июнь 6 278 Июль – сентябрь 7 257 Октябрь – декабрь 8 384 Январь – март 19 х8 9 401 Апрель – июнь 10 360 Июль – сентябрь 11 335 Октябрь – декабрь 12 462

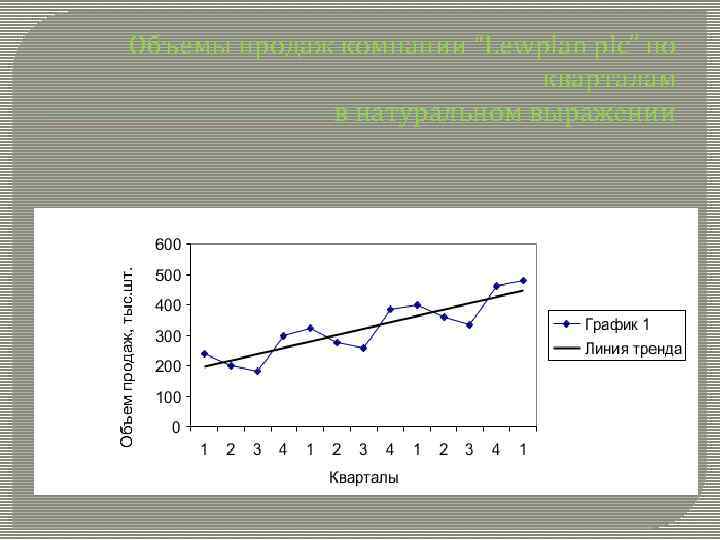Объемы продаж компании “Lewplan plc” по кварталам в натуральном выражении

Процедура анализа и прогноза включает следующие этапы: 1. Расчет значений сезонной компоненты. 2. Исключение сезонной компоненты из фактических наблюдений (десезонализация) и моделирование тренда на основе полученных данных. 3. Проверка точности модели 4. Прогнозирование.

Этап 1 Просуммировав первые четыре значения и разделив полученную сумму на 4, определим средний объем продаж в каждом квартале 19 х6 года: (239 + 201 + 182 + 297 ) / 4 = 229, 75.

Если последовательно продвигаться вперед (т. е. отбросить первое наблюдение, равное 239 и, добавив следующее – 324, разделить сумму на 4 и т. д. ), то можно рассчитать средние квартальные значения на промежутке: апрель 19 х6 – март 19 х7 (251), июнь 19 х6 – июль 19 х7 (270, 25) и т. д.

Рассчитанные значения тренда можно использовать для нахождения оценок сезонной компоненты: У – Т = С + Е, но прежде следует скользящие средние центрировать, чтобы они относились к тем же временным интервалам, что и исходные данные. Так, первая оценка, равная 229, 75, представляет собой точку, совпадающую с серединой 19 х6 года, т. е. лежит в центре промежутка фактических объемов продаж во 2 и 3 кварталах. Вторая оценка, равная 251, лежит между фактическими значениями в 3 и 4 кварталах. Нам же требуются десезонализированные средние значения, которые можно было бы сравнить с фактическими. Найдем среднюю из первой и второй оценок, центрируя их на июль – сентябрь 19 х6 г. , т. е. (229, 75 + 251 ) / 2 = 240, 4, которую можно непосредственно сравнивать с фактическим значением за этот период, равным 182.

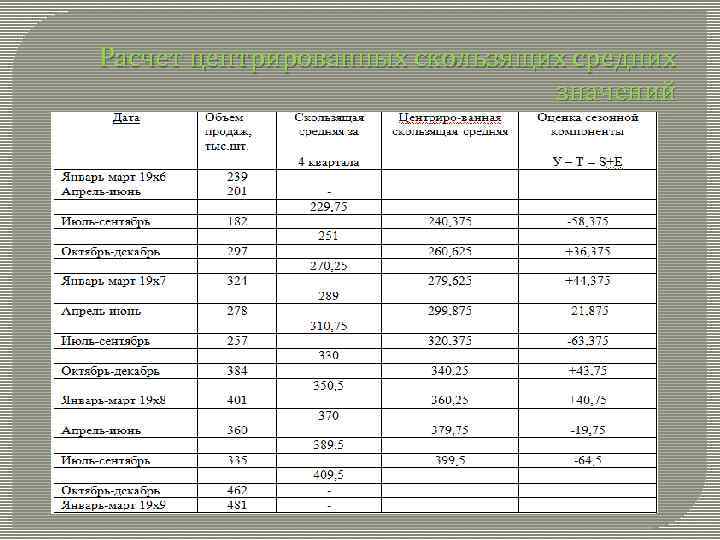Расчет центрированных скользящих средних значений

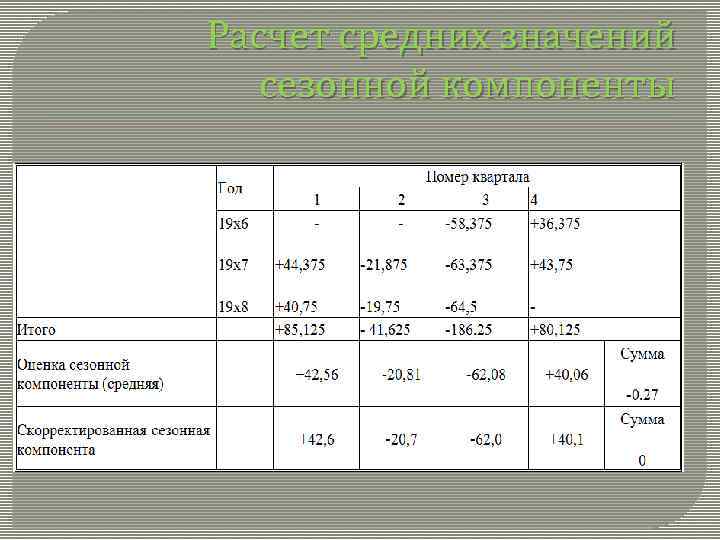Расчет средних значений сезонной компоненты

Этап 2 Десезонализация данных при расчете тренда заключается в вы читании соответствующих значений сезонной компоненты из фактических данных за каждый квартал, т. е. У – С = Т + Е

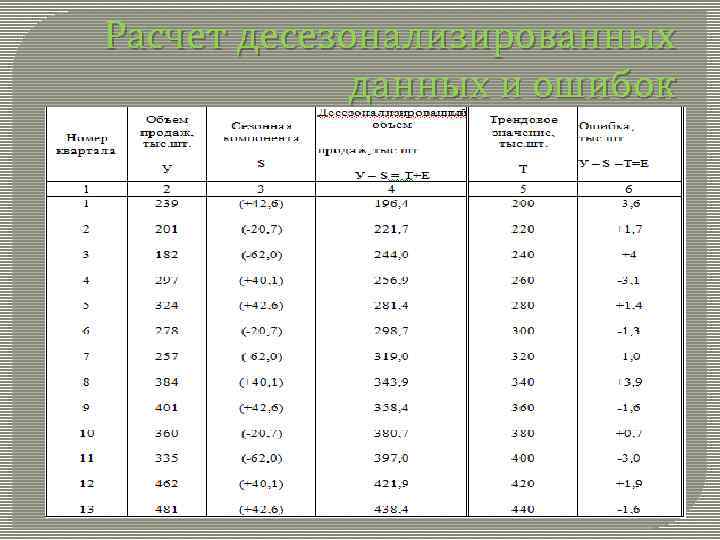Расчет десезонализированных данных и ошибок

Уравнение линии тренда Т = a + b t где a и b характеризуют точку пересечения с осью ординат и наклон лини тренда соответственно, а t – номер квартала. Для определения параметров прямой, наилучшим образом аппроксимирующей тренд, можно использовать метод наименьших квадратов

С помощью калькулятора можно подсчитать t = 91, t 2 = 819, yt = 32746, 2, y = 4158, 6, n = 13. Подставив найденные значения в соответствующие формулы, получим: b = 19, 978, a = 180, 046. Следовательно, уравнение тренда (с учетом округления) имеет вид: Т = 180 +20 t.

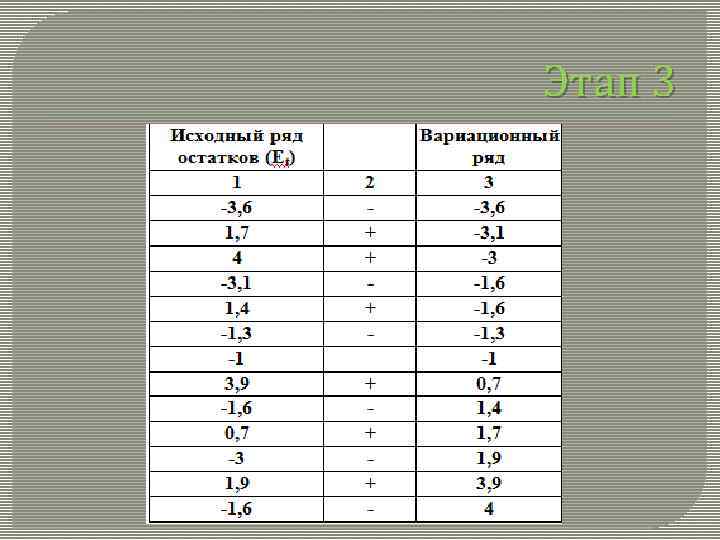Этап 3

Сравнивая фактические значения Kmax и V с критическими, видим, что условия случайности ряда остатков в соответствии с критерием серий выполнены: Kmax = 2 < [3, 3 ( lg n + 1)] = [3, 3 (lg 13 + 1)] = [ 6, 976] = 6 V = 11 > [1/2 ( n +1 – 1, 96 (n-1)2 )] = [1/2 ( 13 +1 – 1, 96 (13 -1)2 )] = [3, 605] = 3.

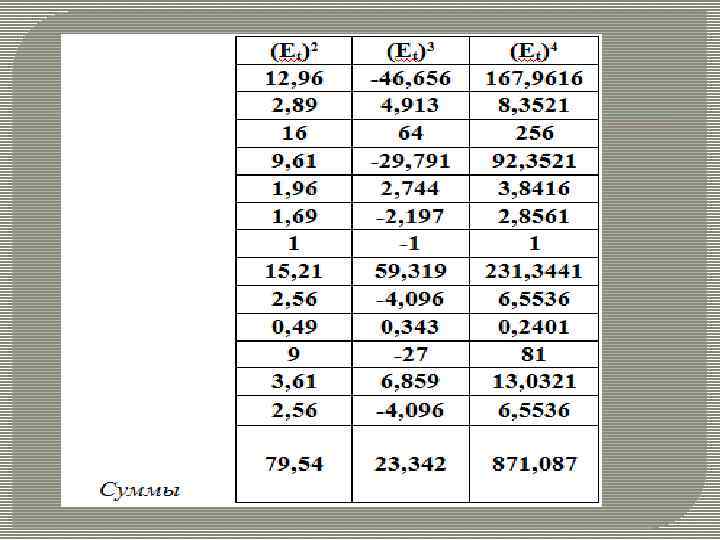
Итак, имеем: А= 0, 1186 < 1, 5 A = 0, 814; Э +6/n+1 = 0, 7815 < 1, 5 Э = 1, 1696. Оба неравенства выполнены, т. е. можно с вероятностью 0, 95 считать наличие нормального закона распределения случайных уровней ряда остатков установленным.

Проверим гипотезу о равенстве нулю математического ожидания остатков: т. е. и это свойство остаточной последовательности выполнено.

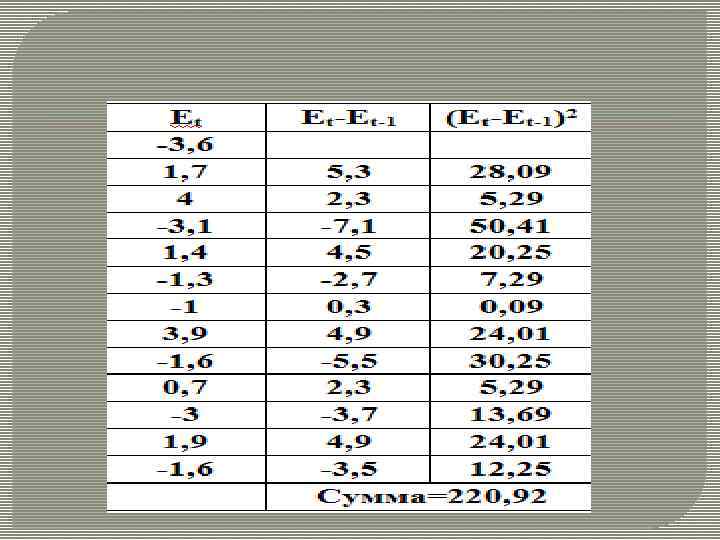
d’ = 4 – d = 1, 223. Табличные значения d-статистики для n = 13: d. H = 1, 01 d. В = 1, 34. Вычисленное значение d-статистики находится между d. H и d. В , поэтому гипотеза о независимости уровней ряда остатков может считаться выполненной условно (нужны дополнительные исследования).

MAD= 28, 8/13=2, 2 MSE= 79, 54/13=6, 1 Как видим, ошибки достаточно малы (составляют от 1 до 2 % по отношению к исходным данным), т. е. выявленная тенденция достаточно устойчива и позволяет получить хорошие краткосрочные прогнозы.

Этап 4 F = T + C (тыс. шт. за квартал) Порядковый номер квартала, включающего ближайшие три месяца с апреля по июль 19 х9 г. равен 14, таким образом, прогнозное трендовое значение составит: Т 14 = 180 + 2014 = 460 (тыс. шт. за квартал). Соответствующая сезонная компонента равна - 20, 7 тыс. шт. (2 -й квартал года). Следовательно, прогноз на этот квартал: F(апрель - июнь 19 х9 г. ) = 4600 – 20, 7 = 439, 3 тыс. шт.