urok_1-2_tema_1.pptx
- Количество слайдов: 66
 Профільна інформатика Лінія “Алгоритмізація та програмування” 10 клас
Профільна інформатика Лінія “Алгоритмізація та програмування” 10 клас
 Тема 1. Основні поняття алгоритмізації (4 уроки)
Тема 1. Основні поняття алгоритмізації (4 уроки)
 План вивчення теми 1 (1 -4 урок) 1 -2. Поняття алгоритму. Властивості алгоритмів. Способи представлення алгоритмів. Базові алгоритмічні структури. Типи алгортмів. Виконавець та системи команд виконавця. Формальне виконання алгоритму. Аргументи, результати, проміжні величини. 3. Практична робота “Способи подання алгоритмів” 4. Практична робота “Базові алгоритмічні структури. Типи алгоритмів”
План вивчення теми 1 (1 -4 урок) 1 -2. Поняття алгоритму. Властивості алгоритмів. Способи представлення алгоритмів. Базові алгоритмічні структури. Типи алгортмів. Виконавець та системи команд виконавця. Формальне виконання алгоритму. Аргументи, результати, проміжні величини. 3. Практична робота “Способи подання алгоритмів” 4. Практична робота “Базові алгоритмічні структури. Типи алгоритмів”
 Поняття алгоритму Слово «алгоритм» походить від «algorithmi» — латинської форми написання імені великого математика аль-Хорезмі, який сформулював правила виконання арифметичних дій. Тому спочатку під алгоритмом розуміли тільки правила виконання чотирьох арифметичних дій над багатоцифровими числами в десятковій системі числення. Зараз він є одним із фундаментальних понять інформатики. Алгоритм — це послідовність дій, спрямованих на розв’язання поставленої задачі. Алгоритмізація – процес розробки алгоритму (плану дій) для розв'язування задачі Алгоритм — це точні розпорядження (вказівки, команди) виконавцеві Відносно здійснення послідовності дій, які спрямовані на розв'язання певної задачі.
Поняття алгоритму Слово «алгоритм» походить від «algorithmi» — латинської форми написання імені великого математика аль-Хорезмі, який сформулював правила виконання арифметичних дій. Тому спочатку під алгоритмом розуміли тільки правила виконання чотирьох арифметичних дій над багатоцифровими числами в десятковій системі числення. Зараз він є одним із фундаментальних понять інформатики. Алгоритм — це послідовність дій, спрямованих на розв’язання поставленої задачі. Алгоритмізація – процес розробки алгоритму (плану дій) для розв'язування задачі Алгоритм — це точні розпорядження (вказівки, команди) виконавцеві Відносно здійснення послідовності дій, які спрямовані на розв'язання певної задачі.
 Поняття алгоритму Кожна людина в повсякденному житті, під час навчання або на роботі вирішує величезну кількість завдань самої різної складності. Деякі із цих завдань настільки прості й звичні, що ми вирішуємо їх не замислюючись, автоматично, і навіть не вважаємо завданнями. До них можна віднести такі завдання, як «Купити хліб» , «Зібратися в школу» , «Закрити двері на ключ» та ін. Інші ж завдання, навпаки, такі важкі, що вимагають тривалих міркувань і зусиль для пошуку розв'язання й досягнення поставленої мети. Наприклад, розв'язання завдань «Написати контрольну роботу на 10» або «Вільно розмовляти іноземною мовою» вимагають виконання набагато більшої кількості складних дій, ніж розв'язання завдання «Купити морозиво» . При цьому рішення навіть найпростішого завдання звичайно здійснюється за кілька послідовних кроків.
Поняття алгоритму Кожна людина в повсякденному житті, під час навчання або на роботі вирішує величезну кількість завдань самої різної складності. Деякі із цих завдань настільки прості й звичні, що ми вирішуємо їх не замислюючись, автоматично, і навіть не вважаємо завданнями. До них можна віднести такі завдання, як «Купити хліб» , «Зібратися в школу» , «Закрити двері на ключ» та ін. Інші ж завдання, навпаки, такі важкі, що вимагають тривалих міркувань і зусиль для пошуку розв'язання й досягнення поставленої мети. Наприклад, розв'язання завдань «Написати контрольну роботу на 10» або «Вільно розмовляти іноземною мовою» вимагають виконання набагато більшої кількості складних дій, ніж розв'язання завдання «Купити морозиво» . При цьому рішення навіть найпростішого завдання звичайно здійснюється за кілька послідовних кроків.
 Процес покупки хліба можна представити так: 1) взяти гроші; 2) піти в магазин; 3) вибрати потрібні хлібобулочні вироби; 4) оплатити вартість покупки; 5) принести хліб додому.
Процес покупки хліба можна представити так: 1) взяти гроші; 2) піти в магазин; 3) вибрати потрібні хлібобулочні вироби; 4) оплатити вартість покупки; 5) принести хліб додому.
 Порядок дій у алгоритмі Аналогічно, у вигляді послідовності дій можна описати процеси розв'язання багатьох завдань, з якими школяр має справу в школі: «Обчислити периметр багатокутника» , «Знайти найбільший загальний дільник двох натуральних чисел» , "Визначити частина мови» , «Провести фонетичний розбір слова» . Така послідовність кроків у розв'язанні завдання називається алгоритмом. При цьому для алгоритму важливий не тільки набір дій, але й те, у якому порядку вони виконуються. Наприклад, спробуємо переставити у відомий вам алгоритм знаходження найменшого загального кратного декількох натуральних чисел і це вже не алгоритм: 1) розкласти вихідні числа на прості множники; 2) знайти добутки множників, що вийшли; 3) виписати множники, що входять у розкладання одного із чисел; 4) дописати до них відсутні множники з розкладань інших чисел.
Порядок дій у алгоритмі Аналогічно, у вигляді послідовності дій можна описати процеси розв'язання багатьох завдань, з якими школяр має справу в школі: «Обчислити периметр багатокутника» , «Знайти найбільший загальний дільник двох натуральних чисел» , "Визначити частина мови» , «Провести фонетичний розбір слова» . Така послідовність кроків у розв'язанні завдання називається алгоритмом. При цьому для алгоритму важливий не тільки набір дій, але й те, у якому порядку вони виконуються. Наприклад, спробуємо переставити у відомий вам алгоритм знаходження найменшого загального кратного декількох натуральних чисел і це вже не алгоритм: 1) розкласти вихідні числа на прості множники; 2) знайти добутки множників, що вийшли; 3) виписати множники, що входять у розкладання одного із чисел; 4) дописати до них відсутні множники з розкладань інших чисел.
 Кожен алгоритм має задовольняти певні властивості Дискретність. • Будь-який алгоритм може бути розбитий на окремі кроки — закінчені дії. Перехід до наступного кроку можливий лише після завершення попереднього. Визначеність (чи детермінованість). • Кожна команда алгоритму повинна однозначно визначати певну дію і не допускати двоякого тлумачення. Строго визначеним повинен бути і порядок виконання операцій. Результативність. • Виконання алгоритму має приводити до конкретного результату — розв'язку задачі, якщо навіть він дає і результати, які можуть виявитися і неправильними. Розв'язком задачі може бути також повідомлення про те, що задача розв'язку не має. Масовість. • За допомогою алгоритму можна розв'язувати не одну конкретну задачу, а безліч однотипних задач. Властивість масовості збільшує практичну цінність алгоритму. Скінченність. • Виконання алгоритму повинно завершитися за скінченну кількість кроків. Виконання алгоритму не може закінчуватися невизначеною ситуацією або ж зовсім не закінчуватися. Правильність. • Алгоритм правильний, якщо його виконання забезпечує досягнення мети. Формальність. • Будь-який виконавець, здатний сприймати і виконувати вказівки алгоритму (навіть не розуміючи їх змісту), діючи за алгоритмом, зможе виконати поставлене завдання.
Кожен алгоритм має задовольняти певні властивості Дискретність. • Будь-який алгоритм може бути розбитий на окремі кроки — закінчені дії. Перехід до наступного кроку можливий лише після завершення попереднього. Визначеність (чи детермінованість). • Кожна команда алгоритму повинна однозначно визначати певну дію і не допускати двоякого тлумачення. Строго визначеним повинен бути і порядок виконання операцій. Результативність. • Виконання алгоритму має приводити до конкретного результату — розв'язку задачі, якщо навіть він дає і результати, які можуть виявитися і неправильними. Розв'язком задачі може бути також повідомлення про те, що задача розв'язку не має. Масовість. • За допомогою алгоритму можна розв'язувати не одну конкретну задачу, а безліч однотипних задач. Властивість масовості збільшує практичну цінність алгоритму. Скінченність. • Виконання алгоритму повинно завершитися за скінченну кількість кроків. Виконання алгоритму не може закінчуватися невизначеною ситуацією або ж зовсім не закінчуватися. Правильність. • Алгоритм правильний, якщо його виконання забезпечує досягнення мети. Формальність. • Будь-який виконавець, здатний сприймати і виконувати вказівки алгоритму (навіть не розуміючи їх змісту), діючи за алгоритмом, зможе виконати поставлене завдання.
 Властивості алгоритму ВЛАСТИВОСТІ АЛГОРИТМУ Виконуючи алгоритм, виконавець може не вникати в зміст того, що він робить, і разом із тим отримати потрібний результат, тобто виконавець діє формально. Тому для правильної побудови алгоритму необхідно знати систему команд виконавця, бути впевненим, що виконання алгоритму завершиться за кінцеве число кроків. Тому кажуть про деякі загальні властивості алгоритмів. ДИСКРЕТНІСТЬ Алгоритм розв’язання задачі повинен складатися з послідовності окремих кроків — відокремлених одна від одної команд (указівок), кожна з яких виконується за кінцевий час. Тільки закінчивши виконання однієї команди, виконавець переходить до виконання іншої.
Властивості алгоритму ВЛАСТИВОСТІ АЛГОРИТМУ Виконуючи алгоритм, виконавець може не вникати в зміст того, що він робить, і разом із тим отримати потрібний результат, тобто виконавець діє формально. Тому для правильної побудови алгоритму необхідно знати систему команд виконавця, бути впевненим, що виконання алгоритму завершиться за кінцеве число кроків. Тому кажуть про деякі загальні властивості алгоритмів. ДИСКРЕТНІСТЬ Алгоритм розв’язання задачі повинен складатися з послідовності окремих кроків — відокремлених одна від одної команд (указівок), кожна з яких виконується за кінцевий час. Тільки закінчивши виконання однієї команди, виконавець переходить до виконання іншої.
 Властивості алгоритмів ВИЗНАЧЕНІСТЬ Визначеність (однозначність). Кожна команда алгоритму однозначно визначає дії виконавця і не припускає подвійного тлумачення. Суворо визначеним є й порядок виконання команд. ФОРМАЛЬНІСТЬ Будь-який виконавець, який володіє заданою системою команд, може виконати заданий алгоритм, не вникаючи в суть задачі.
Властивості алгоритмів ВИЗНАЧЕНІСТЬ Визначеність (однозначність). Кожна команда алгоритму однозначно визначає дії виконавця і не припускає подвійного тлумачення. Суворо визначеним є й порядок виконання команд. ФОРМАЛЬНІСТЬ Будь-який виконавець, який володіє заданою системою команд, може виконати заданий алгоритм, не вникаючи в суть задачі.
 Властивості алгоритмів РЕЗУЛЬТАТИВНІСТЬ Виконання алгоритму не може закінчуватися невизначеною ситуацією або зовсім не закінчуватися. Будь-який алгоритм передбачає, що його виконання при допустимих початкових даних за кінцеве число кроків приведе до очікуваного результату. МАСОВІСТЬ Алгоритм має передбачати можливість зміни початкових (вхідних) даних у деяких допустимих межах і можливість використання його для розв’язання задач одного класу (універсальність алгоритму). Саме через названі властивості часто дається визначення поняття алгоритму як скінченної однозначно визначеної послідовності операцій, формальне виконання якої приводить до розв’язання певної задачі за кінцеве число кроків.
Властивості алгоритмів РЕЗУЛЬТАТИВНІСТЬ Виконання алгоритму не може закінчуватися невизначеною ситуацією або зовсім не закінчуватися. Будь-який алгоритм передбачає, що його виконання при допустимих початкових даних за кінцеве число кроків приведе до очікуваного результату. МАСОВІСТЬ Алгоритм має передбачати можливість зміни початкових (вхідних) даних у деяких допустимих межах і можливість використання його для розв’язання задач одного класу (універсальність алгоритму). Саме через названі властивості часто дається визначення поняття алгоритму як скінченної однозначно визначеної послідовності операцій, формальне виконання якої приводить до розв’язання певної задачі за кінцеве число кроків.
 Основні характеристики виконавця алгоритму Середовище виконавця – умови, у яких може діяти виконавець Елементарні дії – найпростіші дії, які може виконати виконавець Система команд виконавця – сукупність допустимих команд виконавця. Допустимі команди – команди, які зрозумілі виконавцю і можуть бути ними виконані. Недопустимі команди – команди, які не можуть бути виконані виконавцем.
Основні характеристики виконавця алгоритму Середовище виконавця – умови, у яких може діяти виконавець Елементарні дії – найпростіші дії, які може виконати виконавець Система команд виконавця – сукупність допустимих команд виконавця. Допустимі команди – команди, які зрозумілі виконавцю і можуть бути ними виконані. Недопустимі команди – команди, які не можуть бути виконані виконавцем.
 Виконавець алгоритму Кожний алгоритм створюється з розрахунку на конкретного виконавця, тому можна сказати, що алгоритм — це точні розпорядження (указівки, команди, операції, інструкції) виконавцеві здійснити послідовність дій, спрямованих на розв’язання поставленої задачі. Алгоритм складається із команд — окремих указівок виконавцеві виконати деякі конкретні дії. Команди алгоритму виконуються одна за одною, і на кожному кроці відомо, яка команда повинна виконуватися. Почергове виконання команд за кінцеве число кроків приводить до розв’язання задачі. Для того щоб виконавець міг розв’язати задачу за заданим алгоритмом, він повинен уміти виконувати кожну з дій, що вказується командами алгоритму. Виконавцями алгоритмів можуть бути людина, тварини, автомати, тобто ті, хто розуміє та може виконати вказівки алгоритму. Фрезерний станок з числовим програмним управлінням
Виконавець алгоритму Кожний алгоритм створюється з розрахунку на конкретного виконавця, тому можна сказати, що алгоритм — це точні розпорядження (указівки, команди, операції, інструкції) виконавцеві здійснити послідовність дій, спрямованих на розв’язання поставленої задачі. Алгоритм складається із команд — окремих указівок виконавцеві виконати деякі конкретні дії. Команди алгоритму виконуються одна за одною, і на кожному кроці відомо, яка команда повинна виконуватися. Почергове виконання команд за кінцеве число кроків приводить до розв’язання задачі. Для того щоб виконавець міг розв’язати задачу за заданим алгоритмом, він повинен уміти виконувати кожну з дій, що вказується командами алгоритму. Виконавцями алгоритмів можуть бути людина, тварини, автомати, тобто ті, хто розуміє та може виконати вказівки алгоритму. Фрезерний станок з числовим програмним управлінням
 Система команд виконавця — сукупність команд, які можуть бути виконані виконавцем; кожна команда алгоритму входить до системи команд виконавця. В основі роботи автоматичних пристроїв лежить положення, що найпростіші операції, на які розпадається процес розв’язання задачі, може виконати машина, яка спеціально створена для виконання окремих команд алгоритму і виконує їх у послідовності, вказаній в алгоритмі. Токарний станок з ЧПУ
Система команд виконавця — сукупність команд, які можуть бути виконані виконавцем; кожна команда алгоритму входить до системи команд виконавця. В основі роботи автоматичних пристроїв лежить положення, що найпростіші операції, на які розпадається процес розв’язання задачі, може виконати машина, яка спеціально створена для виконання окремих команд алгоритму і виконує їх у послідовності, вказаній в алгоритмі. Токарний станок з ЧПУ
 Подання алгоритмів Процес алгоритмізації — це визначення елементарних дій та порядку їх виконання для розв’язання поставленого завдання. Існують різні способи запису алгоритмів (словесний, формульно-словесний, метод блок-схем, програмний та ін. ), які застосовуються для представлення алгоритму у вигляді, що однозначно розуміється і розробником, і виконавцем алгоритму. Для опису алгоритмів людина часто користується природною мовою, але для запису багатьох алгоритмів природна мова виявилась незручною, тому виникла необхідність у створенні штучних мов, наприклад мови математичних формул, хімічних процесів тощо. Існує спеціальна навчальна алгоритмічна мова, яка була створена для запису алгоритмів на папері; вона використовує слова природної мови, але має більш жорстку структуру. Найбільше поширення для запису логічної структури алгоритмів отримали графічні (структурні) схеми, які спрощують складання та аналіз алгоритму, полегшують перехід від запису алгоритму до написання програми. алг <назва алгоритму> (<тип змінних>) арг <імена змінних-аргументів> рез <імена змінних-результатів> поч <тип та імена проміжних змінних> <тіло алгоритму> кін
Подання алгоритмів Процес алгоритмізації — це визначення елементарних дій та порядку їх виконання для розв’язання поставленого завдання. Існують різні способи запису алгоритмів (словесний, формульно-словесний, метод блок-схем, програмний та ін. ), які застосовуються для представлення алгоритму у вигляді, що однозначно розуміється і розробником, і виконавцем алгоритму. Для опису алгоритмів людина часто користується природною мовою, але для запису багатьох алгоритмів природна мова виявилась незручною, тому виникла необхідність у створенні штучних мов, наприклад мови математичних формул, хімічних процесів тощо. Існує спеціальна навчальна алгоритмічна мова, яка була створена для запису алгоритмів на папері; вона використовує слова природної мови, але має більш жорстку структуру. Найбільше поширення для запису логічної структури алгоритмів отримали графічні (структурні) схеми, які спрощують складання та аналіз алгоритму, полегшують перехід від запису алгоритму до написання програми. алг <назва алгоритму> (<тип змінних>) арг <імена змінних-аргументів> рез <імена змінних-результатів> поч <тип та імена проміжних змінних> <тіло алгоритму> кін
 Подання алгоритмів Алгоритми подаються за допомогою природних або штучних мов, схем, рисунків, знаків тощо Способи подання алгоритмів: Словесний – подання алгоритмів, які призначенні на виконання людиною (наприклад, кулінарних рецептів, правил переходу вулиці тощо) природною мовою в усній або письмовій формі Формульно-словесний – подання алгоритмів у навчальній та науковій діяльності за допомогою мови математичних формул, хімічних процесів тощо зі словесними поясненнями природною мовою. Графічний – подання алгоритмів у вигляді графічних схем (блок-схем або структурних схем) для спрощення розробки та аналізу алгоритмів, полегшення переходу від запису алгоритму до написання програм. Програмний – подання алгоритмів мовою програмування для їх подальшого опрацювання на комп'ютері. Інші способи – специфічні способи подання алгоритмів, такі, як запис музики за допомогою нот тощо.
Подання алгоритмів Алгоритми подаються за допомогою природних або штучних мов, схем, рисунків, знаків тощо Способи подання алгоритмів: Словесний – подання алгоритмів, які призначенні на виконання людиною (наприклад, кулінарних рецептів, правил переходу вулиці тощо) природною мовою в усній або письмовій формі Формульно-словесний – подання алгоритмів у навчальній та науковій діяльності за допомогою мови математичних формул, хімічних процесів тощо зі словесними поясненнями природною мовою. Графічний – подання алгоритмів у вигляді графічних схем (блок-схем або структурних схем) для спрощення розробки та аналізу алгоритмів, полегшення переходу від запису алгоритму до написання програм. Програмний – подання алгоритмів мовою програмування для їх подальшого опрацювання на комп'ютері. Інші способи – специфічні способи подання алгоритмів, такі, як запис музики за допомогою нот тощо.
 Метод блок-схем Блок-схема алгоритму – це графічне зображення алгоритму у вигляді спеціальних блоків із необхідними словесними поясненнями. Кожен етап алгоритму на блок-схемі подається у вигляді геометричної фігури, яка має певну форму залежно від характеру дії. Найчастіше використовуються чотири основні символи: овал, паралелограм, прямокутник і ромб.
Метод блок-схем Блок-схема алгоритму – це графічне зображення алгоритму у вигляді спеціальних блоків із необхідними словесними поясненнями. Кожен етап алгоритму на блок-схемі подається у вигляді геометричної фігури, яка має певну форму залежно від характеру дії. Найчастіше використовуються чотири основні символи: овал, паралелограм, прямокутник і ромб.
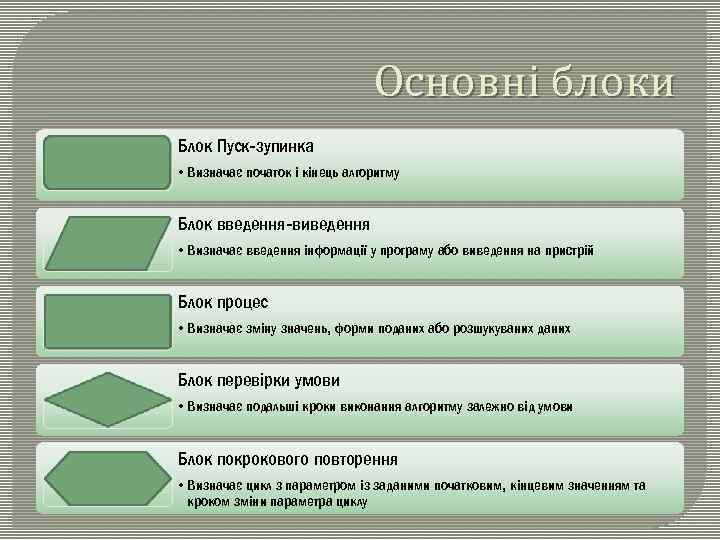 Основні блоки Блок Пуск-зупинка • Визначає початок і кінець алгоритму Блок введення-виведення • Визначає введення інформації у програму або виведення на пристрій Блок процес • Визначає зміну значень, форми поданих або розшукуваних даних Блок перевірки умови • Визначає подальші кроки виконання алгоритму залежно від умови Блок покрокового повторення • Визначає цикл з параметром із заданими початковим, кінцевим значенням та кроком зміни параметра циклу
Основні блоки Блок Пуск-зупинка • Визначає початок і кінець алгоритму Блок введення-виведення • Визначає введення інформації у програму або виведення на пристрій Блок процес • Визначає зміну значень, форми поданих або розшукуваних даних Блок перевірки умови • Визначає подальші кроки виконання алгоритму залежно від умови Блок покрокового повторення • Визначає цикл з параметром із заданими початковим, кінцевим значенням та кроком зміни параметра циклу
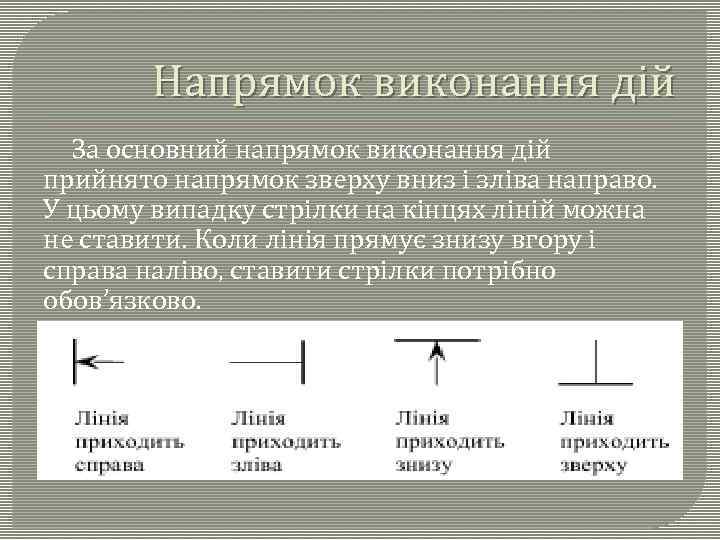 Напрямок виконання дій За основний напрямок виконання дій прийнято напрямок зверху вниз і зліва направо. У цьому випадку стрілки на кінцях ліній можна не ставити. Коли лінія прямує знизу вгору і справа наліво, ставити стрілки потрібно обов’язково.
Напрямок виконання дій За основний напрямок виконання дій прийнято напрямок зверху вниз і зліва направо. У цьому випадку стрілки на кінцях ліній можна не ставити. Коли лінія прямує знизу вгору і справа наліво, ставити стрілки потрібно обов’язково.
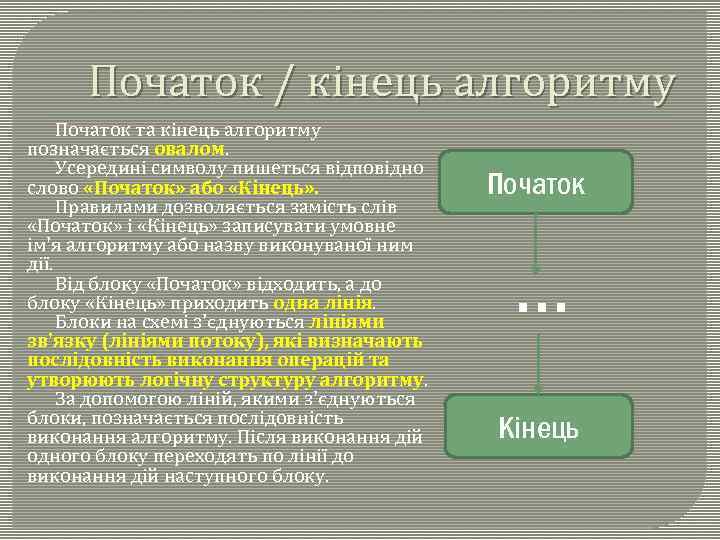 Початок / кінець алгоритму Початок та кінець алгоритму позначається овалом. Усередині символу пишеться відповідно слово «Початок» або «Кінець» . Правилами дозволяється замість слів «Початок» і «Кінець» записувати умовне ім'я алгоритму або назву виконуваної ним дії. Від блоку «Початок» відходить, а до блоку «Кінець» приходить одна лінія. Блоки на схемі з'єднуються лініями зв'язку (лініями потоку), які визначають послідовність виконання операцій та утворюють логічну структуру алгоритму. За допомогою ліній, якими з'єднуються блоки, позначається послідовність виконання алгоритму. Після виконання дій одного блоку переходять по лінії до виконання дій наступного блоку. Початок … Кінець
Початок / кінець алгоритму Початок та кінець алгоритму позначається овалом. Усередині символу пишеться відповідно слово «Початок» або «Кінець» . Правилами дозволяється замість слів «Початок» і «Кінець» записувати умовне ім'я алгоритму або назву виконуваної ним дії. Від блоку «Початок» відходить, а до блоку «Кінець» приходить одна лінія. Блоки на схемі з'єднуються лініями зв'язку (лініями потоку), які визначають послідовність виконання операцій та утворюють логічну структуру алгоритму. За допомогою ліній, якими з'єднуються блоки, позначається послідовність виконання алгоритму. Після виконання дій одного блоку переходять по лінії до виконання дій наступного блоку. Початок … Кінець
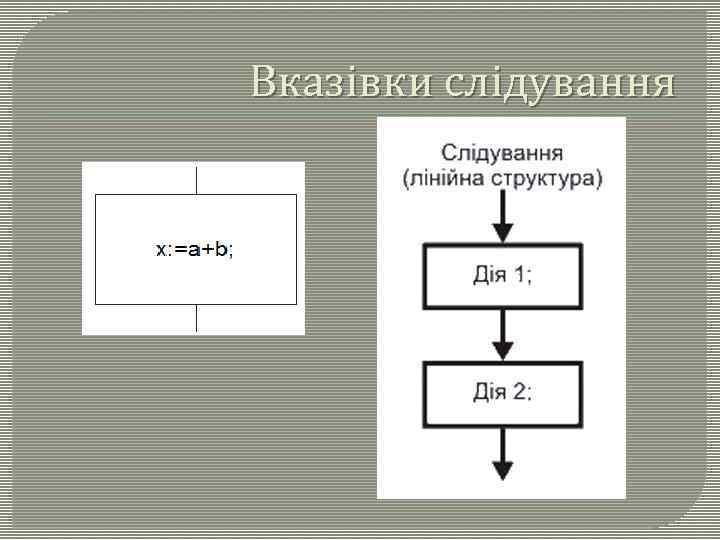 Вказівки слідування
Вказівки слідування
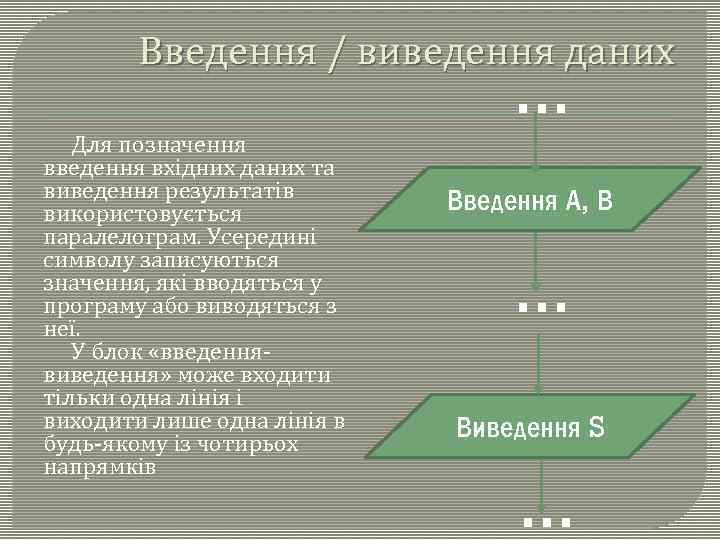 Введення / виведення даних Для позначення введення вхідних даних та виведення результатів використовується паралелограм. Усередині символу записуються значення, які вводяться у програму або виводяться з неї. У блок «введеннявиведення» може входити тільки одна лінія і виходити лише одна лінія в будь-якому із чотирьох напрямків … Введення А, В … Виведення S …
Введення / виведення даних Для позначення введення вхідних даних та виведення результатів використовується паралелограм. Усередині символу записуються значення, які вводяться у програму або виводяться з неї. У блок «введеннявиведення» може входити тільки одна лінія і виходити лише одна лінія в будь-якому із чотирьох напрямків … Введення А, В … Виведення S …
 Вказівка присвоєння (процес) Для позначення дії (процесу) використовується прямокутник. У блок «процес» може входити тільки одна лінія і виходити лише одна лінія в будьякому із чотирьох напрямків m: =2*x+5
Вказівка присвоєння (процес) Для позначення дії (процесу) використовується прямокутник. У блок «процес» може входити тільки одна лінія і виходити лише одна лінія в будьякому із чотирьох напрямків m: =2*x+5
 Запис умови Для позначення перевірки виконання деякої умови та розгалуження обчислювального процесу залежно від результату перевірки цієї умови використовується ромб. Усередині символу записується умова, яка перевіряється. Якщо умова виконується, то далі обчислювальний процес здійснюється за розгалуженням «так» , якщо не виконується — за розгалуженням «ні» . У блок «розгалуження» входить одна лінія, а виходять дві лінії. так x>0 ні
Запис умови Для позначення перевірки виконання деякої умови та розгалуження обчислювального процесу залежно від результату перевірки цієї умови використовується ромб. Усередині символу записується умова, яка перевіряється. Якщо умова виконується, то далі обчислювальний процес здійснюється за розгалуженням «так» , якщо не виконується — за розгалуженням «ні» . У блок «розгалуження» входить одна лінія, а виходять дві лінії. так x>0 ні
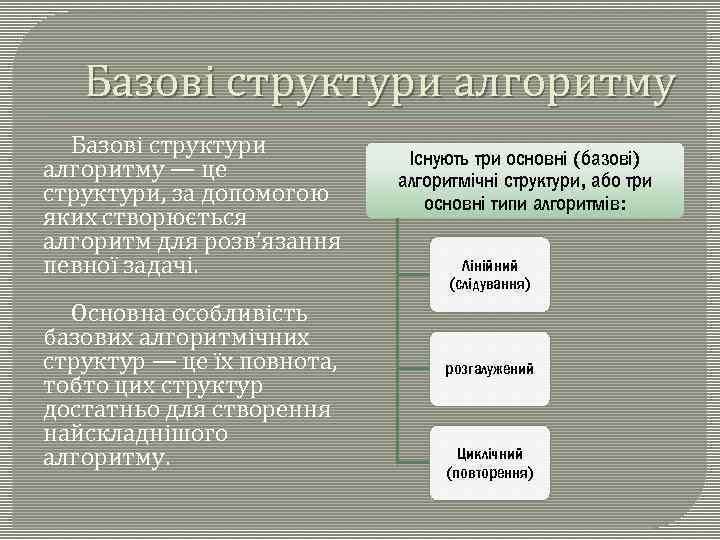 Базові структури алгоритму — це структури, за допомогою яких створюється алгоритм для розв’язання певної задачі. Основна особливість базових алгоритмічних структур — це їх повнота, тобто цих структур достатньо для створення найскладнішого алгоритму. Існують три основні (базові) алгоритмічні структури, або три основні типи алгоритмів: Лінійний (слідування) розгалужений Циклічний (повторення)
Базові структури алгоритму — це структури, за допомогою яких створюється алгоритм для розв’язання певної задачі. Основна особливість базових алгоритмічних структур — це їх повнота, тобто цих структур достатньо для створення найскладнішого алгоритму. Існують три основні (базові) алгоритмічні структури, або три основні типи алгоритмів: Лінійний (слідування) розгалужений Циклічний (повторення)
 Структура слідування – це структура, яка передбачає одноразове виконання заданої послідовності дій. Структура реалізується через лінійний алгоритм. Серія 1 Серія 2 Лінійний алгоритм (послідовне виконання, структура слідування) — це алгоритм, який забезпечує отримання результату шляхом одноразового виконання послідовності дій, незалежно від вхідних даних і проміжних результатів. Дії в таких алгоритмах виконуються послідовно, одна за однією, тобто лінійно. Іноді використовують напівформальну мову з обмеженим словником (часто на основі англійської мови), проміжний між природною мовою та мовою програмування. Така мова називається псевдокод. Запис алгоритму на псевдокоді називається структурним планом. Псевдокод зручний тим, що дозволяє програмістові зосередитися на формулюванні алгоритму, не замислюючись над синтаксичними особливостями конкретної мови програмування. Псевдокод: Алгоритм <назва> Початок <Послідовність дій> Кінець
Структура слідування – це структура, яка передбачає одноразове виконання заданої послідовності дій. Структура реалізується через лінійний алгоритм. Серія 1 Серія 2 Лінійний алгоритм (послідовне виконання, структура слідування) — це алгоритм, який забезпечує отримання результату шляхом одноразового виконання послідовності дій, незалежно від вхідних даних і проміжних результатів. Дії в таких алгоритмах виконуються послідовно, одна за однією, тобто лінійно. Іноді використовують напівформальну мову з обмеженим словником (часто на основі англійської мови), проміжний між природною мовою та мовою програмування. Така мова називається псевдокод. Запис алгоритму на псевдокоді називається структурним планом. Псевдокод зручний тим, що дозволяє програмістові зосередитися на формулюванні алгоритму, не замислюючись над синтаксичними особливостями конкретної мови програмування. Псевдокод: Алгоритм <назва> Початок <Послідовність дій> Кінець
 Будь-який алгоритм може бути представлений у вигляді послідовності дій. Під дією розуміють або базову операцію, або базову структуру. В якості базових операцій використовуються: Ø операція присвоювання виду <ім'я змінної >: = <вираз> Ø операція вводу/виводу: ввід (список введення) ; висновок (список виведення). Зміст операції присвоєння полягає в обчисленні результату виразу, що стоїть праворуч від знака «: =» , для конкретних значень назв змінних і присвоєнні цього результату змінній, що стоїть ліворуч від знака «: =» , наприклад: D: = 5 D: = D +1 Min: = C
Будь-який алгоритм може бути представлений у вигляді послідовності дій. Під дією розуміють або базову операцію, або базову структуру. В якості базових операцій використовуються: Ø операція присвоювання виду <ім'я змінної >: = <вираз> Ø операція вводу/виводу: ввід (список введення) ; висновок (список виведення). Зміст операції присвоєння полягає в обчисленні результату виразу, що стоїть праворуч від знака «: =» , для конкретних значень назв змінних і присвоєнні цього результату змінній, що стоїть ліворуч від знака «: =» , наприклад: D: = 5 D: = D +1 Min: = C
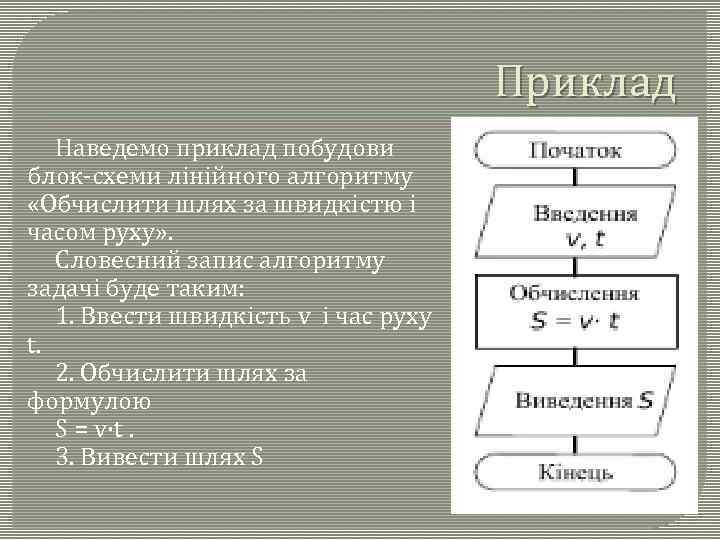 Приклад Наведемо приклад побудови блок-схеми лінійного алгоритму «Обчислити шлях за швидкістю і часом руху» . Словесний запис алгоритму задачі буде таким: 1. Ввести швидкість v і час руху t. 2. Обчислити шлях за формулою S = v·t. 3. Вивести шлях S
Приклад Наведемо приклад побудови блок-схеми лінійного алгоритму «Обчислити шлях за швидкістю і часом руху» . Словесний запис алгоритму задачі буде таким: 1. Ввести швидкість v і час руху t. 2. Обчислити шлях за формулою S = v·t. 3. Вивести шлях S
 Приклад Алгоритм «Обчислити площу трикутника за трьома сторонами» . Словесний запис алгоритму: 1. Ввести сторони трикутника а, b, с. 2. Обчислити півпериметр трикутника 0. 5*(a+b+c) 3. Обчислити площу S за формулою Герона 4. Вивести площу трикутника S. Запис алгоритму у вигляді блок-схеми буде таким:
Приклад Алгоритм «Обчислити площу трикутника за трьома сторонами» . Словесний запис алгоритму: 1. Ввести сторони трикутника а, b, с. 2. Обчислити півпериметр трикутника 0. 5*(a+b+c) 3. Обчислити площу S за формулою Герона 4. Вивести площу трикутника S. Запис алгоритму у вигляді блок-схеми буде таким:
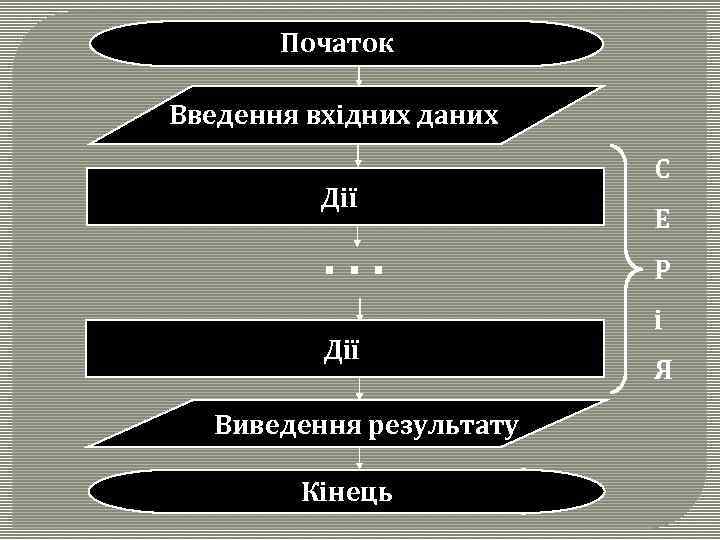 Початок Введення вхідних даних Дії . . . Дії Виведення результату Кінець С Е Р і Я
Початок Введення вхідних даних Дії . . . Дії Виведення результату Кінець С Е Р і Я
 Побудова алгоритму Для розв'язування задач за допомогою комп'ютера існують різні технології програмування, наприклад, низхідне програмування (“зверху донизу”), висхідне (“знизу вгору”), пакетне, об'єктноорієнтоване тощо і відповідно різні прийоми розробки алгоритму
Побудова алгоритму Для розв'язування задач за допомогою комп'ютера існують різні технології програмування, наприклад, низхідне програмування (“зверху донизу”), висхідне (“знизу вгору”), пакетне, об'єктноорієнтоване тощо і відповідно різні прийоми розробки алгоритму
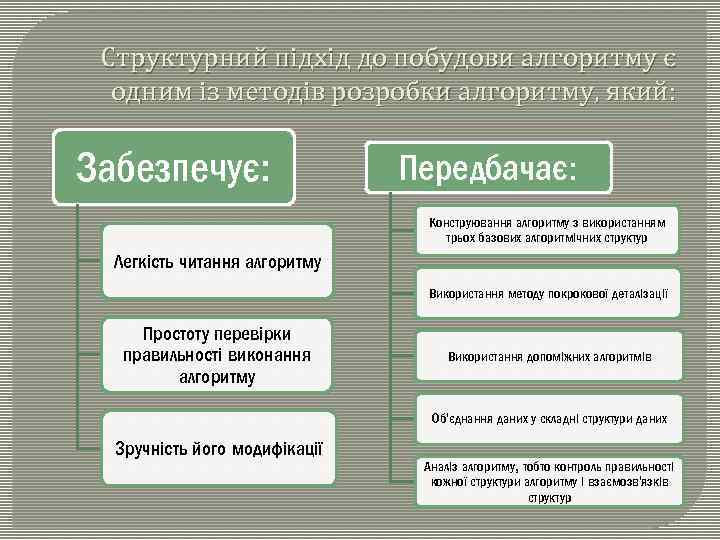 Структурний підхід до побудови алгоритму є одним із методів розробки алгоритму, який: Забезпечує: Передбачає: Конструювання алгоритму з використанням трьох базових алгоритмічних структур Легкість читання алгоритму Використання методу покрокової деталізації Простоту перевірки правильності виконання алгоритму Використання допоміжних алгоритмів Об'єднання даних у складні структури даних Зручність його модифікації Аналіз алгоритму, тобто контроль правильності кожної структури алгоритму і взаємозв'язків структур
Структурний підхід до побудови алгоритму є одним із методів розробки алгоритму, який: Забезпечує: Передбачає: Конструювання алгоритму з використанням трьох базових алгоритмічних структур Легкість читання алгоритму Використання методу покрокової деталізації Простоту перевірки правильності виконання алгоритму Використання допоміжних алгоритмів Об'єднання даних у складні структури даних Зручність його модифікації Аналіз алгоритму, тобто контроль правильності кожної структури алгоритму і взаємозв'язків структур
 Метод покрокової деталізації це метод проектування алгоритму “зверху донизу”. Для реалізації цього методу потрібно виконати такі дії: Розбити складну задачу на декілька простих Якщо задачі чергового рівня стають досить простими для незалежного розв'язання, закінчити процес деталізації Скласти для кожної простої задачі свій допоміжний алгоритм, при необхідності дані об'єднати у структури Скомпонувати результати проектування простих задач в єдиний алгоритм Проаналізувати роботу алгоритму
Метод покрокової деталізації це метод проектування алгоритму “зверху донизу”. Для реалізації цього методу потрібно виконати такі дії: Розбити складну задачу на декілька простих Якщо задачі чергового рівня стають досить простими для незалежного розв'язання, закінчити процес деталізації Скласти для кожної простої задачі свій допоміжний алгоритм, при необхідності дані об'єднати у структури Скомпонувати результати проектування простих задач в єдиний алгоритм Проаналізувати роботу алгоритму
 Допоміжні алгоритми Допоміжний алгоритм – алгоритм, який призначений для розв'язання допоміжної задачі, виділеної в окрему структуру. Призначення допоміжних алгоритмів Полегшення розробки алгоритму для розв'язання складних задач Надання наочності, зрозумілості основному алгоритму Скороченість і ефективність основного алгоритму
Допоміжні алгоритми Допоміжний алгоритм – алгоритм, який призначений для розв'язання допоміжної задачі, виділеної в окрему структуру. Призначення допоміжних алгоритмів Полегшення розробки алгоритму для розв'язання складних задач Надання наочності, зрозумілості основному алгоритму Скороченість і ефективність основного алгоритму
 Допоміжний алгоритм ОСОБЛИВОСТІ ДОПОМІЖНОГО АЛГОРИТМУ Унікальне ім'я, за яким його можна розпізнати серед інших допоміжних алгоритмів і викликати з іншого алгоритму ПАРАМЕТРИ ДОПОМІЖНОГО АЛГОРИТМУ Формальні параметри – параметри, які використовуються для опису вхідних та вихідних даних допоміжного алгоритму Фактичні параметри – параметри, з якими виконується допоміжний алгоритм. Наявність списку параметрів, за допомогою яких здійснюється виконання алгоритму з необхідними вхідними даними (аргументами 0і/або передавання вихідних даних (результатів)до іншого алгоритму. Кількість, тип та призначення формальних та фактичних параметрів повинні збігатися
Допоміжний алгоритм ОСОБЛИВОСТІ ДОПОМІЖНОГО АЛГОРИТМУ Унікальне ім'я, за яким його можна розпізнати серед інших допоміжних алгоритмів і викликати з іншого алгоритму ПАРАМЕТРИ ДОПОМІЖНОГО АЛГОРИТМУ Формальні параметри – параметри, які використовуються для опису вхідних та вихідних даних допоміжного алгоритму Фактичні параметри – параметри, з якими виконується допоміжний алгоритм. Наявність списку параметрів, за допомогою яких здійснюється виконання алгоритму з необхідними вхідними даними (аргументами 0і/або передавання вихідних даних (результатів)до іншого алгоритму. Кількість, тип та призначення формальних та фактичних параметрів повинні збігатися
 Види допоміжних алгоритмів Алгоритми-процедури – це допоміжні алгоритми, результатом виконання яких є одне або декілька значень, що надаються фактичним параметрам, або деяка дія. Алгоритми-функції - це допоміжні алгоритми. результатом виконання яких є одне значення, що присвоюється безпосередньо імені функції.
Види допоміжних алгоритмів Алгоритми-процедури – це допоміжні алгоритми, результатом виконання яких є одне або декілька значень, що надаються фактичним параметрам, або деяка дія. Алгоритми-функції - це допоміжні алгоритми. результатом виконання яких є одне значення, що присвоюється безпосередньо імені функції.
 Виклик допоміжного алгоритму Виклик алгоритмупроцедури здійснюється за допомогою спеціальних інструкцій, а виклик алгоритму-функції – безпосередньою вказівкою імені функції в деякому виразі. Після виконання допоміжного алгоритму виконується наступна команда основного алгоритму, що міститься після команди виклику допоміжного алгоритму. Схема виконання вказівки виклику допоміжного алгоритму: Формальні аргументи допоміжного алгоритму змінюються на фактичні значення, вказані в команді виклику алгоритму Виконуються команди допоміжного алгоритму з використанням фактичних параметрів Отримані результати надаються фактичним параметрам, які використовуються як фактичні результати в алгоритмах-процедурах, або імені самого алгоритму-функції.
Виклик допоміжного алгоритму Виклик алгоритмупроцедури здійснюється за допомогою спеціальних інструкцій, а виклик алгоритму-функції – безпосередньою вказівкою імені функції в деякому виразі. Після виконання допоміжного алгоритму виконується наступна команда основного алгоритму, що міститься після команди виклику допоміжного алгоритму. Схема виконання вказівки виклику допоміжного алгоритму: Формальні аргументи допоміжного алгоритму змінюються на фактичні значення, вказані в команді виклику алгоритму Виконуються команди допоміжного алгоритму з використанням фактичних параметрів Отримані результати надаються фактичним параметрам, які використовуються як фактичні результати в алгоритмах-процедурах, або імені самого алгоритму-функції.
 Логічні вирази та логічні операції Висловлювання – це деяке мовне ствердження, яке має зміст і відносно якого можна сказати, що воно істинне або хибне. Тобто кожному висловлюванню можна приписати істиннісне (логічне) значення “істинність” (“ 1”, “true”) або “хибність” (“ 0”, “false”). Використовуючи частку “ні” (“не”), сполучники “і” (“та”), “або” та інші, можуть будуватися нові висловлювання. Побудова нового висловлювання з наданих висловлювань називається логічною операцією. Знаки логічних операцій називають логічними зв'язками. Висловлювання, які утворені з інших висловлювань за допомогою логічних операцій і мають у структурі логічні зв'язки, називаються складеними висловлюваннями. На відміну від них у простих висловлюваннях такі зв'язки відсутні.
Логічні вирази та логічні операції Висловлювання – це деяке мовне ствердження, яке має зміст і відносно якого можна сказати, що воно істинне або хибне. Тобто кожному висловлюванню можна приписати істиннісне (логічне) значення “істинність” (“ 1”, “true”) або “хибність” (“ 0”, “false”). Використовуючи частку “ні” (“не”), сполучники “і” (“та”), “або” та інші, можуть будуватися нові висловлювання. Побудова нового висловлювання з наданих висловлювань називається логічною операцією. Знаки логічних операцій називають логічними зв'язками. Висловлювання, які утворені з інших висловлювань за допомогою логічних операцій і мають у структурі логічні зв'язки, називаються складеними висловлюваннями. На відміну від них у простих висловлюваннях такі зв'язки відсутні.
 Логічні операції NOT, AND, OR Логічна операція “not” • “інверсія” (заперечення) – операція, яка при застосуванні до висловлювання А (not A) надає значення, протилежне значенню А. Логічна операція “and” • “кон’юнкція” (логічне множення або логічне “і”) – операція, що зв'язує два логічних висловлювання і дає істиннісне значення тільки у тому випадку, коли істинними є обидва висловлювання Логічна операція “or” • “диз’юнкція” (логічне додавання або логічне “або”) – операція, що зв'язує два логічних висловлювання і дає істиннісне значення у тому випадку, коли хоч одне із висловлювань істинне.
Логічні операції NOT, AND, OR Логічна операція “not” • “інверсія” (заперечення) – операція, яка при застосуванні до висловлювання А (not A) надає значення, протилежне значенню А. Логічна операція “and” • “кон’юнкція” (логічне множення або логічне “і”) – операція, що зв'язує два логічних висловлювання і дає істиннісне значення тільки у тому випадку, коли істинними є обидва висловлювання Логічна операція “or” • “диз’юнкція” (логічне додавання або логічне “або”) – операція, що зв'язує два логічних висловлювання і дає істиннісне значення у тому випадку, коли хоч одне із висловлювань істинне.
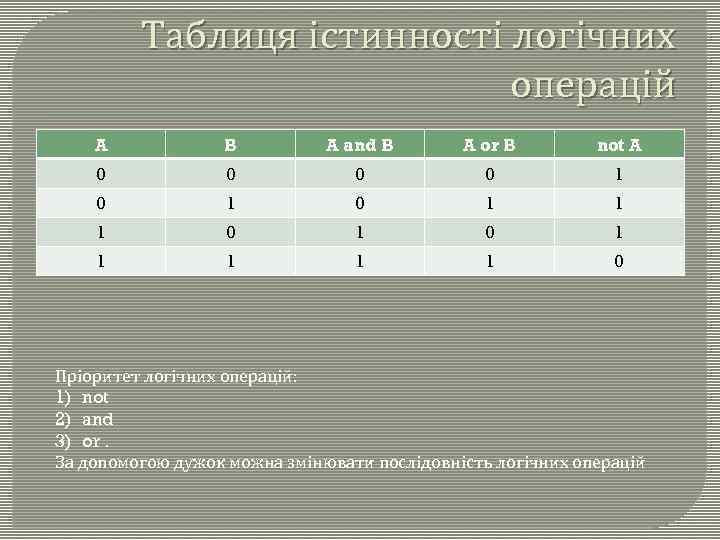 Таблиця істинності логічних операцій A B A and B A or B not A 0 0 1 0 1 0 1 1 1 1 1 0 Пріоритет логічних операцій: 1) not 2) and 3) or. За допомогою дужок можна змінювати послідовність логічних операцій
Таблиця істинності логічних операцій A B A and B A or B not A 0 0 1 0 1 0 1 1 1 1 1 0 Пріоритет логічних операцій: 1) not 2) and 3) or. За допомогою дужок можна змінювати послідовність логічних операцій
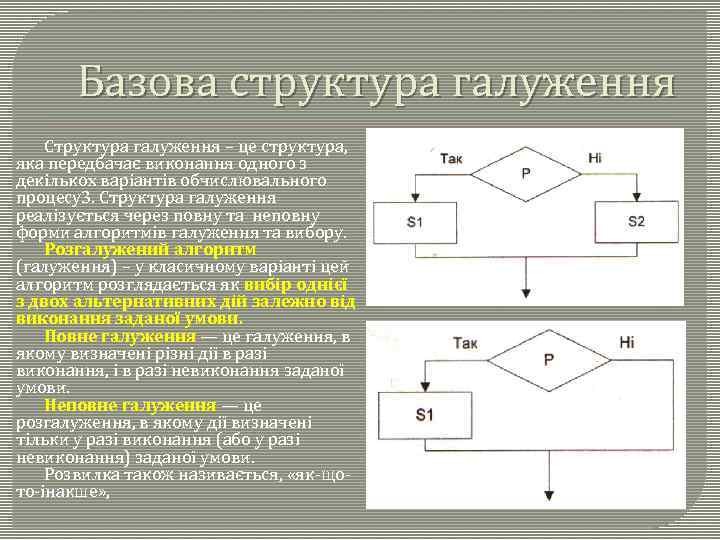 Базова структура галуження Структура галуження – це структура, яка передбачає виконання одного з декількох варіантів обчислювального процесу3. Структура галуження реалізується через повну та неповну форми алгоритмів галуження та вибору. Розгалужений алгоритм (галуження) – у класичному варіанті цей алгоритм розглядається як вибір однієї з двох альтернативних дій залежно від виконання заданої умови. Повне галуження — це галуження, в якому визначені різні дії в разі виконання, і в разі невиконання заданої умови. Неповне галуження — це розгалуження, в якому дії визначені тільки у разі виконання (або у разі невиконання) заданої умови. Розвилка також називається, «як-щото-інакше» ,
Базова структура галуження Структура галуження – це структура, яка передбачає виконання одного з декількох варіантів обчислювального процесу3. Структура галуження реалізується через повну та неповну форми алгоритмів галуження та вибору. Розгалужений алгоритм (галуження) – у класичному варіанті цей алгоритм розглядається як вибір однієї з двох альтернативних дій залежно від виконання заданої умови. Повне галуження — це галуження, в якому визначені різні дії в разі виконання, і в разі невиконання заданої умови. Неповне галуження — це розгалуження, в якому дії визначені тільки у разі виконання (або у разі невиконання) заданої умови. Розвилка також називається, «як-щото-інакше» ,
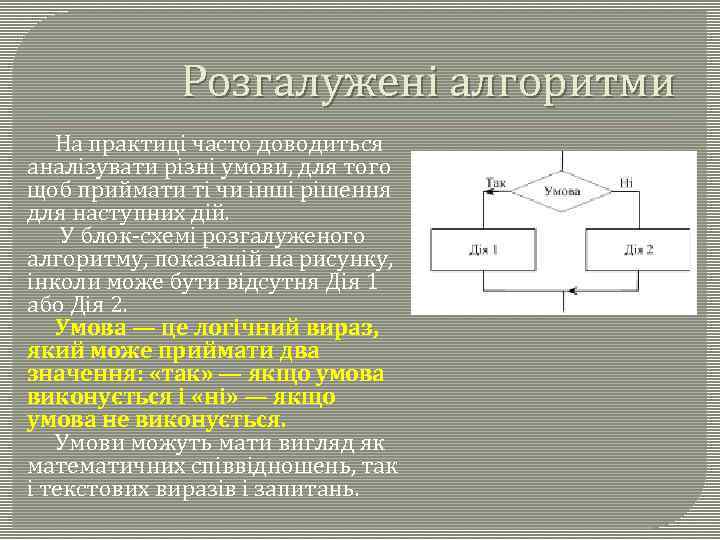 Розгалужені алгоритми На практиці часто доводиться аналізувати різні умови, для того щоб приймати ті чи інші рішення для наступних дій. У блок-схемі розгалуженого алгоритму, показаній на рисунку, інколи може бути відсутня Дія 1 або Дія 2. Умова — це логічний вираз, який може приймати два значення: «так» — якщо умова виконується і «ні» — якщо умова не виконується. Умови можуть мати вигляд як математичних співвідношень, так і текстових виразів і запитань.
Розгалужені алгоритми На практиці часто доводиться аналізувати різні умови, для того щоб приймати ті чи інші рішення для наступних дій. У блок-схемі розгалуженого алгоритму, показаній на рисунку, інколи може бути відсутня Дія 1 або Дія 2. Умова — це логічний вираз, який може приймати два значення: «так» — якщо умова виконується і «ні» — якщо умова не виконується. Умови можуть мати вигляд як математичних співвідношень, так і текстових виразів і запитань.
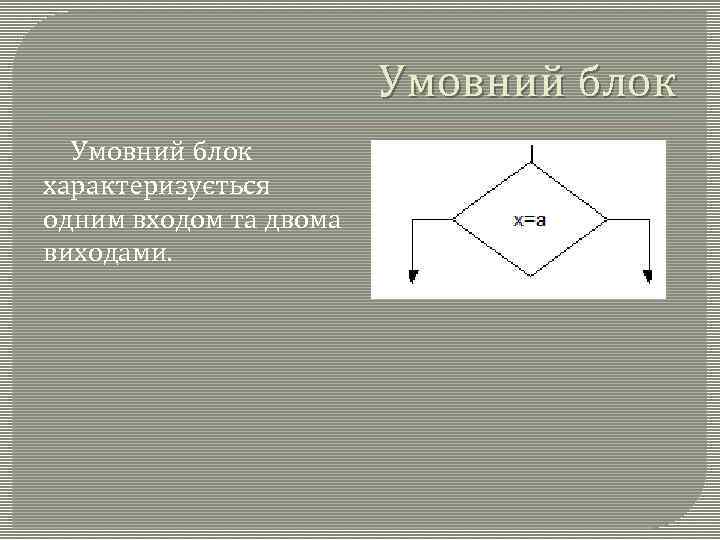 Умовний блок характеризується одним входом та двома виходами.
Умовний блок характеризується одним входом та двома виходами.
 Базова структура повторення Типи структур Цикл цикл «від до» цикл «поки» цикл «до» Циклічний алгоритм (цикл, структура повторення) — це алгоритм, у якому передбачено повторення деякої серії команд. За допомогою цієї структури описуються однотипні дії, що повторюються декілька разів. Такі алгоритми забезпечують виконання довгої послідовності дій, записаних порівняно короткою послідовністю команд. Саме використання циклів дозволяє у повній мірі реалізувати швидкодію комп’ютерів. Основна особливість базових алгоритмічних структур — це їх повнота, тобто цих структур достатньо для створення найскладнішого алгоритму. Третьою базовою структурою є Цикл, який передбачає повторне виконання певних дій, необхідне для більшості програм.
Базова структура повторення Типи структур Цикл цикл «від до» цикл «поки» цикл «до» Циклічний алгоритм (цикл, структура повторення) — це алгоритм, у якому передбачено повторення деякої серії команд. За допомогою цієї структури описуються однотипні дії, що повторюються декілька разів. Такі алгоритми забезпечують виконання довгої послідовності дій, записаних порівняно короткою послідовністю команд. Саме використання циклів дозволяє у повній мірі реалізувати швидкодію комп’ютерів. Основна особливість базових алгоритмічних структур — це їх повнота, тобто цих структур достатньо для створення найскладнішого алгоритму. Третьою базовою структурою є Цикл, який передбачає повторне виконання певних дій, необхідне для більшості програм.
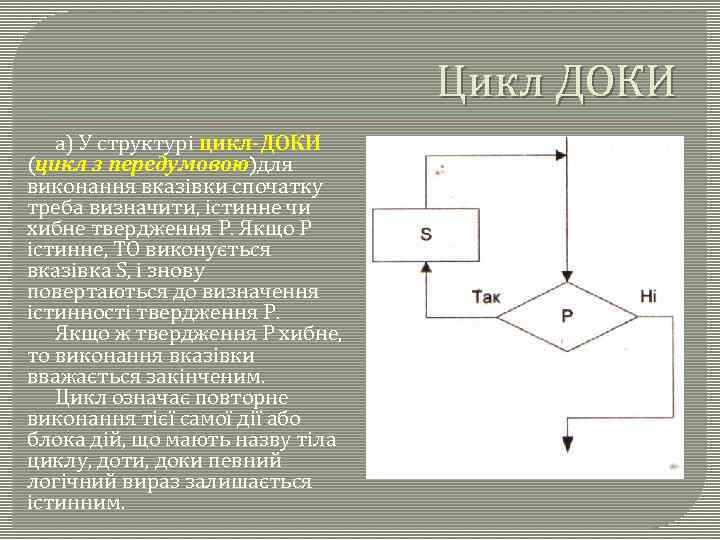 Цикл ДОКИ а) У структурі цикл-ДОКИ (цикл з передумовою)для виконання вказівки спочатку треба визначити, істинне чи хибне твердження Р. Якщо Р істинне, ТО виконується вказівка S, і знову повертаються до визначення істинності твердження Р. Якщо ж твердження Р хибне, то виконання вказівки вважається закінченим. Цикл означає повторне виконання тієї самої дії або блока дій, що мають назву тіла циклу, доти, доки певний логічний вираз залишається істинним.
Цикл ДОКИ а) У структурі цикл-ДОКИ (цикл з передумовою)для виконання вказівки спочатку треба визначити, істинне чи хибне твердження Р. Якщо Р істинне, ТО виконується вказівка S, і знову повертаються до визначення істинності твердження Р. Якщо ж твердження Р хибне, то виконання вказівки вважається закінченим. Цикл означає повторне виконання тієї самої дії або блока дій, що мають назву тіла циклу, доти, доки певний логічний вираз залишається істинним.
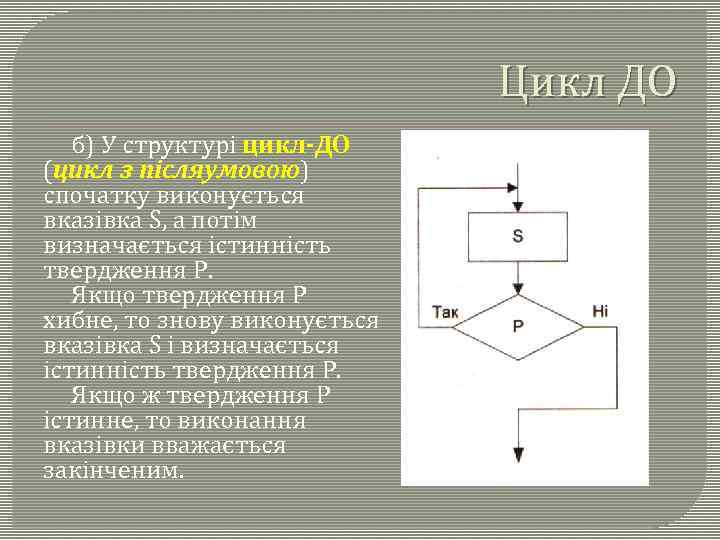 Цикл ДО б) У структурі цикл-ДО (цикл з післяумовою) спочатку виконується вказівка S, а потім визначається істинність твердження Р. Якщо твердження Р хибне, то знову виконується вказівка S і визначається істинність твердження Р. Якщо ж твердження Р істинне, то виконання вказівки вважається закінченим.
Цикл ДО б) У структурі цикл-ДО (цикл з післяумовою) спочатку виконується вказівка S, а потім визначається істинність твердження Р. Якщо твердження Р хибне, то знову виконується вказівка S і визначається істинність твердження Р. Якщо ж твердження Р істинне, то виконання вказівки вважається закінченим.
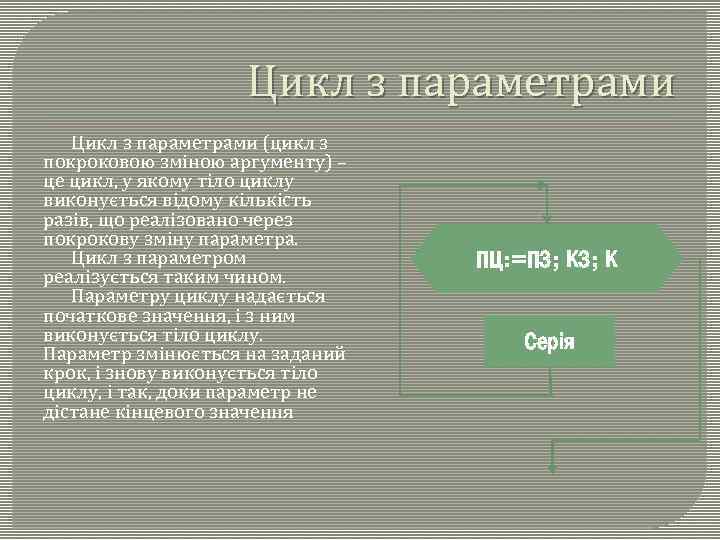 Цикл з параметрами (цикл з покроковою зміною аргументу) – це цикл, у якому тіло циклу виконується відому кількість разів, що реалізовано через покрокову зміну параметра. Цикл з параметром реалізується таким чином. Параметру циклу надається початкове значення, і з ним виконується тіло циклу. Параметр змінюється на заданий крок, і знову виконується тіло циклу, і так, доки параметр не дістане кінцевого значення ПЦ: =ПЗ; К Серія
Цикл з параметрами (цикл з покроковою зміною аргументу) – це цикл, у якому тіло циклу виконується відому кількість разів, що реалізовано через покрокову зміну параметра. Цикл з параметром реалізується таким чином. Параметру циклу надається початкове значення, і з ним виконується тіло циклу. Параметр змінюється на заданий крок, і знову виконується тіло циклу, і так, доки параметр не дістане кінцевого значення ПЦ: =ПЗ; К Серія
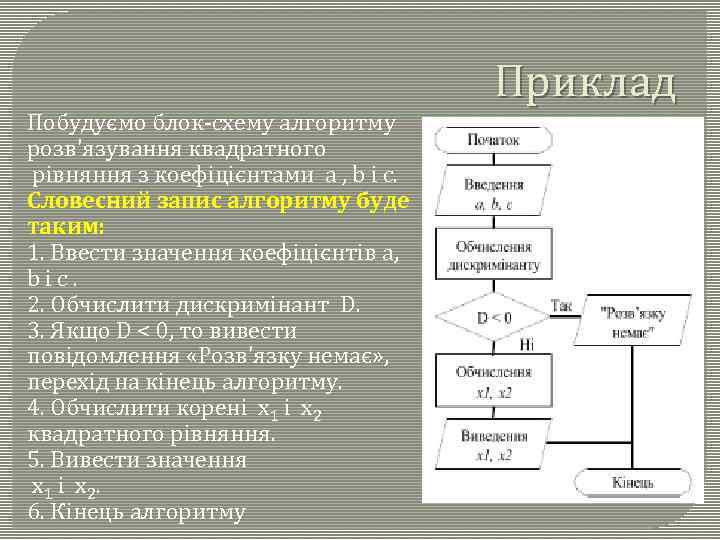 Побудуємо блок-схему алгоритму розв'язування квадратного рівняння з коефіцієнтами а , b і c. Словесний запис алгоритму буде таким: 1. Ввести значення коефіцієнтів a, bіc. 2. Обчислити дискримінант D. 3. Якщо D < 0, то вивести повідомлення «Розв'язку немає» , перехід на кінець алгоритму. 4. Обчислити корені x 1 і x 2 квадратного рівняння. 5. Вивести значення x 1 і x 2. 6. Кінець алгоритму Приклад
Побудуємо блок-схему алгоритму розв'язування квадратного рівняння з коефіцієнтами а , b і c. Словесний запис алгоритму буде таким: 1. Ввести значення коефіцієнтів a, bіc. 2. Обчислити дискримінант D. 3. Якщо D < 0, то вивести повідомлення «Розв'язку немає» , перехід на кінець алгоритму. 4. Обчислити корені x 1 і x 2 квадратного рівняння. 5. Вивести значення x 1 і x 2. 6. Кінець алгоритму Приклад
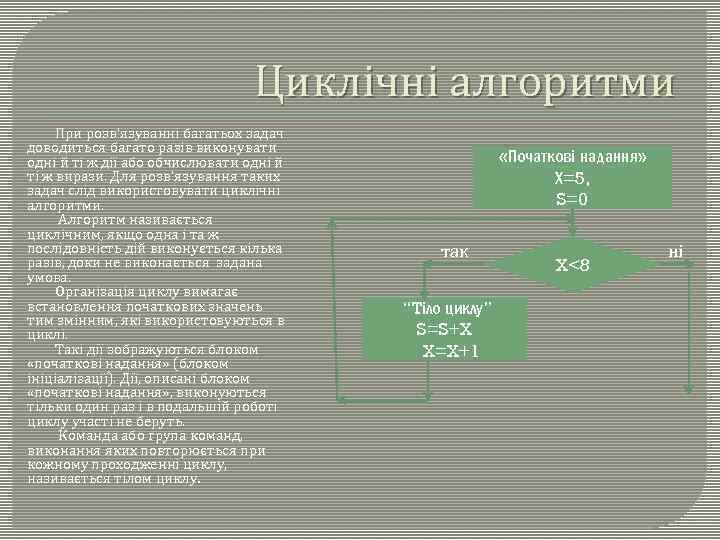 Циклічні алгоритми При розв'язуванні багатьох задач доводиться багато разів виконувати одні й ті ж дії або обчислювати одні й ті ж вирази. Для розв'язування таких задач слід використовувати циклічні алгоритми. Алгоритм називається циклічним, якщо одна і та ж послідовність дій виконується кілька разів, доки не виконається задана умова. Організація циклу вимагає встановлення початкових значень тим змінним, які використовуються в циклі. Такі дії зображуються блоком «початкові надання» (блоком ініціалізації). Дії, описані блоком «початкові надання» , виконуються тільки один раз і в подальшій роботі циклу участі не беруть. Команда або група команд, виконання яких повторюється при кожному проходженні циклу, називається тілом циклу. «Початкові надання» Х=5, S=0 так “Tіло циклу” S=S+X X=X+1 X<8 ні
Циклічні алгоритми При розв'язуванні багатьох задач доводиться багато разів виконувати одні й ті ж дії або обчислювати одні й ті ж вирази. Для розв'язування таких задач слід використовувати циклічні алгоритми. Алгоритм називається циклічним, якщо одна і та ж послідовність дій виконується кілька разів, доки не виконається задана умова. Організація циклу вимагає встановлення початкових значень тим змінним, які використовуються в циклі. Такі дії зображуються блоком «початкові надання» (блоком ініціалізації). Дії, описані блоком «початкові надання» , виконуються тільки один раз і в подальшій роботі циклу участі не беруть. Команда або група команд, виконання яких повторюється при кожному проходженні циклу, називається тілом циклу. «Початкові надання» Х=5, S=0 так “Tіло циклу” S=S+X X=X+1 X<8 ні
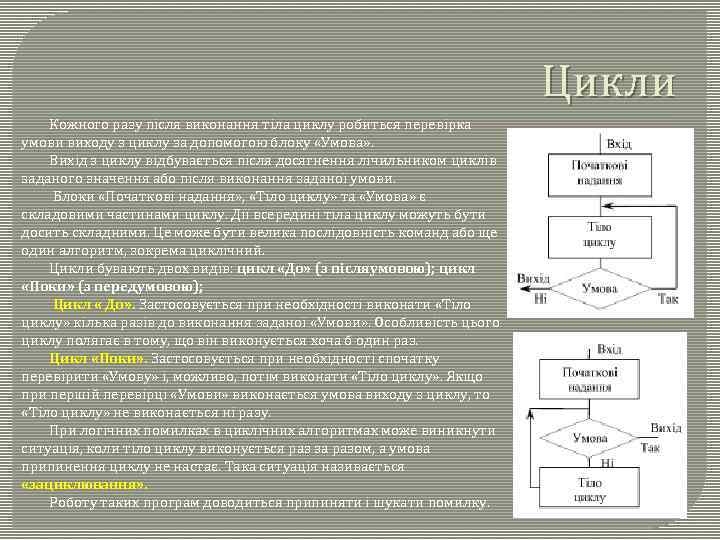 Цикли Кожного разу після виконання тіла циклу робиться перевірка умови виходу з циклу за допомогою блоку «Умова» . Вихід з циклу відбувається після досягнення лічильником циклів заданого значення або після виконання заданої умови. Блоки «Початкові надання» , «Тіло циклу» та «Умова» є складовими частинами циклу. Дії всередині тіла циклу можуть бути досить складними. Це може бути велика послідовність команд або ще один алгоритм, зокрема циклічний. Цикли бувають двох видів: цикл «До» (з післяумовою); цикл «Поки» (з передумовою); Цикл « До» . Застосовується при необхідності виконати «Тіло циклу» кілька разів до виконання заданої «Умови» . Особливість цього циклу полягає в тому, що він виконується хоча б один раз. Цикл «Поки» . Застосовується при необхідності спочатку перевірити «Умову» і, можливо, потім виконати «Тіло циклу» . Якщо при першій перевірці «Умови» виконається умова виходу з циклу, то «Тіло циклу» не виконається ні разу. При логічних помилках в циклічних алгоритмах може виникнути ситуація, коли тіло циклу виконується раз за разом, а умова припинення циклу не настає. Така ситуація називається «зациклювання» . Роботу таких програм доводиться припиняти і шукати помилку.
Цикли Кожного разу після виконання тіла циклу робиться перевірка умови виходу з циклу за допомогою блоку «Умова» . Вихід з циклу відбувається після досягнення лічильником циклів заданого значення або після виконання заданої умови. Блоки «Початкові надання» , «Тіло циклу» та «Умова» є складовими частинами циклу. Дії всередині тіла циклу можуть бути досить складними. Це може бути велика послідовність команд або ще один алгоритм, зокрема циклічний. Цикли бувають двох видів: цикл «До» (з післяумовою); цикл «Поки» (з передумовою); Цикл « До» . Застосовується при необхідності виконати «Тіло циклу» кілька разів до виконання заданої «Умови» . Особливість цього циклу полягає в тому, що він виконується хоча б один раз. Цикл «Поки» . Застосовується при необхідності спочатку перевірити «Умову» і, можливо, потім виконати «Тіло циклу» . Якщо при першій перевірці «Умови» виконається умова виходу з циклу, то «Тіло циклу» не виконається ні разу. При логічних помилках в циклічних алгоритмах може виникнути ситуація, коли тіло циклу виконується раз за разом, а умова припинення циклу не настає. Така ситуація називається «зациклювання» . Роботу таких програм доводиться припиняти і шукати помилку.
 Правила розташування блоків Для графічних алгоритмів існують правила розташування блоків. Головні з цих правил: 1) При послідовному обчисленні стрілки можна не ставити; 2) При циклічному обчисленні стрілки обов’язково потрібно ставити; 3) Стрілка, яка вказує напрямок для вирахувань не може перетинати іншу стрілку. Які помилки чи неточності допущені у даній блоксхемі?
Правила розташування блоків Для графічних алгоритмів існують правила розташування блоків. Головні з цих правил: 1) При послідовному обчисленні стрілки можна не ставити; 2) При циклічному обчисленні стрілки обов’язково потрібно ставити; 3) Стрілка, яка вказує напрямок для вирахувань не може перетинати іншу стрілку. Які помилки чи неточності допущені у даній блоксхемі?
 Цикли ПОСЛІДОВНІ ЦИКЛИ Послідовні цикли – це алгоритми, у яких циклічні структури слідують одна за одною, тобто лінійно ВКЛАДЕНІ ЦИКЛИ Вкладений цикл – це цикл, який використовується як команда в тілі іншого циклу. Рекурентними називаються формули, які надають можливість поточного значення елемента деякої послідовності за її попереднім значенням. Наприклад, обчислення елемента арифметичної чи геометричної прогресії, чисел Фібоначчі, суми чи добутку послідовності тощо. Обчислення за рекурентними формулами часто використовуються в циклічних алгоритмах.
Цикли ПОСЛІДОВНІ ЦИКЛИ Послідовні цикли – це алгоритми, у яких циклічні структури слідують одна за одною, тобто лінійно ВКЛАДЕНІ ЦИКЛИ Вкладений цикл – це цикл, який використовується як команда в тілі іншого циклу. Рекурентними називаються формули, які надають можливість поточного значення елемента деякої послідовності за її попереднім значенням. Наприклад, обчислення елемента арифметичної чи геометричної прогресії, чисел Фібоначчі, суми чи добутку послідовності тощо. Обчислення за рекурентними формулами часто використовуються в циклічних алгоритмах.
 Послідовність розробки алгоритмів складається з таких етапів: Ввід початкових даних; Аналіз виняткових ситуацій; Ініціалізація (присвоєння змінним їх початкових значень) Рішення; Зверніть увагу, що деякі етапи можуть бути відсутніми. Підготовка до виводу; Вивід.
Послідовність розробки алгоритмів складається з таких етапів: Ввід початкових даних; Аналіз виняткових ситуацій; Ініціалізація (присвоєння змінним їх початкових значень) Рішення; Зверніть увагу, що деякі етапи можуть бути відсутніми. Підготовка до виводу; Вивід.
 До уваги! Існують і критерії оптимізації: 1) Мінімальна кількість обчислювальних операцій; 2) Мінімальні кількість логічних блоків; 3) Мінімальна кількість змінних.
До уваги! Існують і критерії оптимізації: 1) Мінімальна кількість обчислювальних операцій; 2) Мінімальні кількість логічних блоків; 3) Мінімальна кількість змінних.
 Поняття величини Базовим поняттям математичних і природних наук є поняття величини, що характеризує стани деякого об’єкта або явища. Значення та позначення величин. Припустимо, ми отримали деяке повідомлення N разом з відповідною йому інформацією I. Інформацію I називають значенням величини, а повідомлення N — позначенням величини. Кажуть, «позначенню N відповідає значення I» . Наприклад, «X = 5» означає, що величина, позначена як Х, має значення 5. З точки зору алгоритмізації як величини та їх сукупності виступають дані, що обробляються цим алгоритмом.
Поняття величини Базовим поняттям математичних і природних наук є поняття величини, що характеризує стани деякого об’єкта або явища. Значення та позначення величин. Припустимо, ми отримали деяке повідомлення N разом з відповідною йому інформацією I. Інформацію I називають значенням величини, а повідомлення N — позначенням величини. Кажуть, «позначенню N відповідає значення I» . Наприклад, «X = 5» означає, що величина, позначена як Х, має значення 5. З точки зору алгоритмізації як величини та їх сукупності виступають дані, що обробляються цим алгоритмом.
 Поняття величини Аргументи та результати. Для роботи багатьох алгоритмів необхідно задавати початкові значення, які передаються в алгоритм за допомогою аргументів — величин, значення яких необхідно задати для виконання алгоритму. Результат — це величина, значення якої буде отримано внаслідок виконання алгоритму. Також для опису алгоритму використовуються проміжні величини — величини, які додатково вводяться автором алгоритму під час його розробки.
Поняття величини Аргументи та результати. Для роботи багатьох алгоритмів необхідно задавати початкові значення, які передаються в алгоритм за допомогою аргументів — величин, значення яких необхідно задати для виконання алгоритму. Результат — це величина, значення якої буде отримано внаслідок виконання алгоритму. Також для опису алгоритму використовуються проміжні величини — величини, які додатково вводяться автором алгоритму під час його розробки.
 Змінні та сталі величини Сталою величиною (константою) називається величина, значення якої не змінюється в процесі виконання алгоритму. Змінною називається величина, значення якої може мінятися в процесі виконання алгоритму. У кожний момент часу змінна величина має деяке значення, яке називається поточним значенням. Саме над величинами виконуються певні операції. Якщо в процесі виконання алгоритму якась величина не набула значення, кажуть, що дана величина не визначена. При написанні алгоритму величинам даються відповідні імена (ідентифікатори), що використовуються для звернення до значення деякої величини. Алгоритм роботи над величинами записується з використанням імен цих величин, але на кожному кроці виконання алгоритму дії проводяться з поточними значеннями величин. У процесі виконання алгоритму значення величини може мінятися: їй присвоюється нове значення, а старе при цьому втрачається.
Змінні та сталі величини Сталою величиною (константою) називається величина, значення якої не змінюється в процесі виконання алгоритму. Змінною називається величина, значення якої може мінятися в процесі виконання алгоритму. У кожний момент часу змінна величина має деяке значення, яке називається поточним значенням. Саме над величинами виконуються певні операції. Якщо в процесі виконання алгоритму якась величина не набула значення, кажуть, що дана величина не визначена. При написанні алгоритму величинам даються відповідні імена (ідентифікатори), що використовуються для звернення до значення деякої величини. Алгоритм роботи над величинами записується з використанням імен цих величин, але на кожному кроці виконання алгоритму дії проводяться з поточними значеннями величин. У процесі виконання алгоритму значення величини може мінятися: їй присвоюється нове значення, а старе при цьому втрачається.
 Інтерактивна вправа Метод «Коло ідей» (За блок-схемою зробити аналіз задачі, що нею реалізується) У малих групах (спікер, секретар, посередник, доповідач) відповісти на такі запитання: 1) визначити ті алгоритми, в основу яких покладено структуру слідування; 2) визначити ті алгоритми, в основу яких покладено структуру з повним розгалуженням; 3) визначити ті алгоритми, в основу яких покладено структуру повторення; 4) визначити ті алгоритми, в основу яких покладено структуру з неповним розгалуженням; 5) визначити ті алгоритми, які подані у словесній формі. Група експертів аналізує результати роботи груп. Доповідач групи експертів повідомляє, як групи впоралися із завданням.
Інтерактивна вправа Метод «Коло ідей» (За блок-схемою зробити аналіз задачі, що нею реалізується) У малих групах (спікер, секретар, посередник, доповідач) відповісти на такі запитання: 1) визначити ті алгоритми, в основу яких покладено структуру слідування; 2) визначити ті алгоритми, в основу яких покладено структуру з повним розгалуженням; 3) визначити ті алгоритми, в основу яких покладено структуру повторення; 4) визначити ті алгоритми, в основу яких покладено структуру з неповним розгалуженням; 5) визначити ті алгоритми, які подані у словесній формі. Група експертів аналізує результати роботи груп. Доповідач групи експертів повідомляє, як групи впоралися із завданням.
 Інтерактивна вправа
Інтерактивна вправа
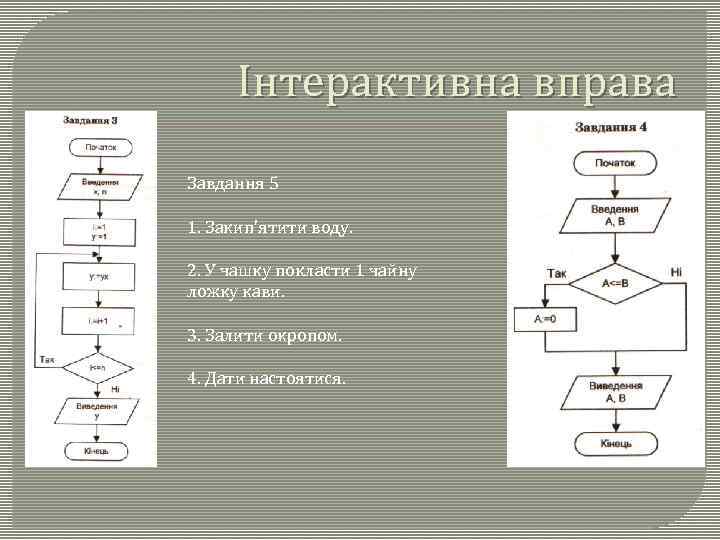 Інтерактивна вправа Завдання 5 1. Закип'ятити воду. 2. У чашку покласти 1 чайну ложку кави. 3. Залити окропом. 4. Дати настоятися.
Інтерактивна вправа Завдання 5 1. Закип'ятити воду. 2. У чашку покласти 1 чайну ложку кави. 3. Залити окропом. 4. Дати настоятися.
 Тренувальні вправи Дано довжини сторін A, B, C трикутника. Знайти площу трикутника S. Побудуйте блок-схему алгоритму розв'язку поставленої задачі. Початок введення: A, B, C P= S= Виведення: S Кінець
Тренувальні вправи Дано довжини сторін A, B, C трикутника. Знайти площу трикутника S. Побудуйте блок-схему алгоритму розв'язку поставленої задачі. Початок введення: A, B, C P= S= Виведення: S Кінець
 Тренувальні вправи Дано координати вершин трикутника АВС. Знайти його площу. Складіть блок-схему алгоритму розв'язку поставленої задачі. Початок введення: x 1, y 1, x 2, y 2, x 3, y 3 A= ( x 2 - x 1 ) 2 + ( y 2 - y 1 ) 2 B= C= P= S= Виведення : S Кінець
Тренувальні вправи Дано координати вершин трикутника АВС. Знайти його площу. Складіть блок-схему алгоритму розв'язку поставленої задачі. Початок введення: x 1, y 1, x 2, y 2, x 3, y 3 A= ( x 2 - x 1 ) 2 + ( y 2 - y 1 ) 2 B= C= P= S= Виведення : S Кінець
 Тренувальні вправи В квадратній кімнаті шириною A і висотою B є вікно і двері з розмірами C на D і M на N відповідно. Обчисліть площу стін для обклеювання їх шпалерами. Складіть блоксхему алгоритму розв'язування поставленої задачі. Початок Введення: A, B, C, D, M, N S 1= 4 * A * B S 2 = C * D S 3 = M * N S = S 1 – (S 2 + S 3) Виведення : S Кінець
Тренувальні вправи В квадратній кімнаті шириною A і висотою B є вікно і двері з розмірами C на D і M на N відповідно. Обчисліть площу стін для обклеювання їх шпалерами. Складіть блоксхему алгоритму розв'язування поставленої задачі. Початок Введення: A, B, C, D, M, N S 1= 4 * A * B S 2 = C * D S 3 = M * N S = S 1 – (S 2 + S 3) Виведення : S Кінець
 Тренувальні вправи Дана величина A, що виражає об'єм інформації в байтах. Перевести А в більші одиниці виміру інформації. Складіть блок-схему алгоритму розв'язання поставленої задачі. Початок Введення : A K = A / 1024 M = K /1024 G = M / 1024 T = G / 1024 Виведення : K, M, G, T Кінець
Тренувальні вправи Дана величина A, що виражає об'єм інформації в байтах. Перевести А в більші одиниці виміру інформації. Складіть блок-схему алгоритму розв'язання поставленої задачі. Початок Введення : A K = A / 1024 M = K /1024 G = M / 1024 T = G / 1024 Виведення : K, M, G, T Кінець
 Тренувальні вправи За даною блок-схемою обчисліть значення деякої функції, відновіть умову задачі; напишіть формулу обчислення значення функції. Y= Початок введення: X A = X 2 B = A 2 C=A+B D=B+1 Y=C/D виведення: Y Кінець
Тренувальні вправи За даною блок-схемою обчисліть значення деякої функції, відновіть умову задачі; напишіть формулу обчислення значення функції. Y= Початок введення: X A = X 2 B = A 2 C=A+B D=B+1 Y=C/D виведення: Y Кінець
 Підсумок уроків 1) Чи досягли ми мети, яку поставили перед собою на початку уроку? Завдяки чому? Що допомогло у засвоєнні матеріалу уроку? 2) Що було легко, а що — складно? 3) Що найбільше запам'яталося на сьогоднішньому уроці? 4) Які ви знаєте базові структури алгоритмів? 5) Які ви засвоїли форми подання алгоритмів? 6) Від чого залежить форма подання алгоритмів? 7) Що таке конструювання алгоритмів? 8) Хто визначає, якою саме базовою структурою треба скористатися в тому чи іншому алгоритмі?
Підсумок уроків 1) Чи досягли ми мети, яку поставили перед собою на початку уроку? Завдяки чому? Що допомогло у засвоєнні матеріалу уроку? 2) Що було легко, а що — складно? 3) Що найбільше запам'яталося на сьогоднішньому уроці? 4) Які ви знаєте базові структури алгоритмів? 5) Які ви засвоїли форми подання алгоритмів? 6) Від чого залежить форма подання алгоритмів? 7) Що таке конструювання алгоритмів? 8) Хто визначає, якою саме базовою структурою треба скористатися в тому чи іншому алгоритмі?


