Prof Lic Javier Velásquez Espinoza La conjunción

Prof. Lic. Javier Velásquez Espinoza * La conjunción se desarrolló con la ayuda del Taller de Pensamiento Lógico de la U. de Loga, a cargo de Jorge Arrmijos (Coor. ).

LÓGICA Es la ciencia que estudia el razonamiento inductivo y deductivo. El razonamiento inductivo es aquel que permite llegar a conclusiones generales a partir de observaciones particulares, por el contrario, el razonamiento deductivo nos permite llegar a conclusiones particulares a partir de observaciones generales. ENUNCIADO: Es toda frase u oración que informa, expresa o dictamina alguna idea a través de afirmaciones o negaciones, preguntas, expresiones de emoción o de saludo, órdenes, etc. ENUNCIADO ABIERTO: Es un enunciado en forma de expresión matemática que no es verdadero ni falso. Ejemplos: x<9 x + 2 = 10 a+b=1 a 2 + b 2 = c 2

PROPOSICIÓN LÓGICA (enunciado cerrado) es un enunciado informativo que admite la posibilidad de ser Verdadero o Falso, pero no ambos a la vez. La veracidad o falsedad de una proposición se denomina “Valor de verdad de la proposición”. SON PROPOSICIONES: NO SON PROPOSICIONES: 39 es un número primo ( F) Resuelve este problema Ambato queda en la Sierra ( V) ¿Puedes prestarme tu libro? 1/2 < 1/4 ( F) Buenos días profesor

CLASES DE PROPOSICIONES Las proposiciones se clasificar en proposiciones simples o atómicas y proposiciones compuestas o moleculares.

PROPOSICIÓN SIMPLE Es aquella que contiene una sola afirmación y se simboliza con las letras p, q, r, s, t, …. . a las que llamaremos variables proposicionales. Otra manera de entender una proposición simple es decir que no se puede descomponer. Ejemplos: p: Todo organismo viviente se adapta a su medio físico. q: Si un número es divisible por 4 también lo es por 2. Ejemplos: VALOR DE VERDAD 1. 15 es un número primo 2. Quito es la capital del Ecuador 3. 32 = 9 : p : q : r ( F) (V) (F)

PROPOSICIONES COMPUESTAS Son aquellas que están formadas por dos o más proposiciones simples o es la negación de una proposición simple. Para que una parte de un enunciado sea un componente de ese enunciado: 1) La parte tiene que ser un enunciado por derecho propio; 2) La parte en el enunciado más largo se reemplaza por otro enunciado, el resultado de este reemplazo tiene que ser significativo, tiene que tener sentido. (p. 365) En toda proposición compuesta las proposiciones simples están ligadas mediante palabras conocidas como conectivos lógicos.

CONECTIVOS LÓGICOS Son palabras que permiten relacionar dos proposiciones o negar una proposición simple. Cuando se les representan por símbolos se les llama operadores lógicos. Los siguientes conectivos son los más recurrentes: 1. “si y sólo si” 2. “o. . . o” 3. “si…entonces…” 4. “o” 5. “y” 6. “no”

CONECTIVOS LÓGICOS OPERADOR LÓGICO LÓGICA SIMBÓLICA Negación Conjunción Disyunción TERMINOLOGÍA LÓGICA no ˄ y o Disyunción exclusiva o en sentido excluyente Conjunción negativa ni…. ni Disyunción negativa no…no Condicional Bicondicional Si…. , entonces Si y sólo si

UNA VEZ MÁS… PROPOSICIONES COMPUESTAS O MOLECULARES Son aquellos enunciados que están formados por dos o más proposiciones simples y unidos por operador lógico. Ejemplos: p: La niña María canta y su hermano Luis toca el piano. q: Ecuador es un país amazónico y latinoamericano.

EL LENGUAJE SIMBÓLICO Los símbolos permiten llegar al meollo de un argumento, mostrar su naturaleza esencial y dejar de lado lo que no es esencial. Con el lenguaje artificial se puede formular con precisión la relación lógica entre las proposiciones. Recordatorio El objetivo fundamental de la lógica deductiva es discernir los argumentos válidos de los inválidos.

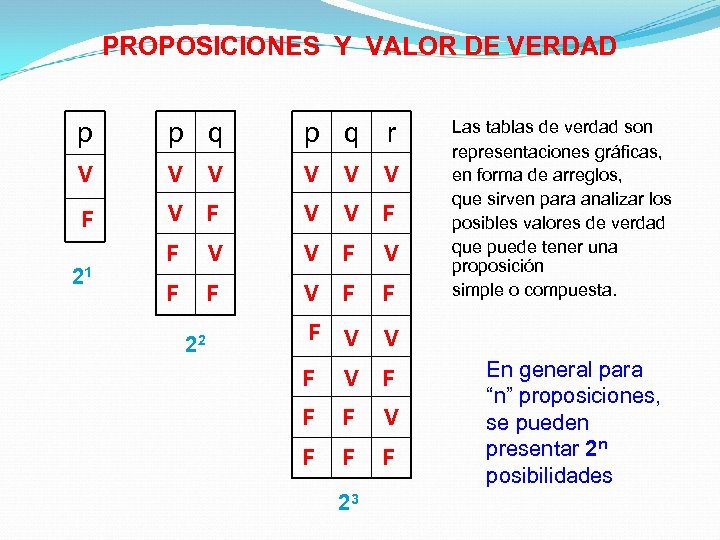PROPOSICIONES Y VALOR DE VERDAD p p q r V V V F F V V F F F V V F F F 21 22 23 Las tablas de verdad son representaciones gráficas, en forma de arreglos, que sirven para analizar los posibles valores de verdad que puede tener una proposición simple o compuesta. En general para “n” proposiciones, se pueden presentar 2 n posibilidades

DEFINICIÓN DE ALGUNOS ENUNCIADOS COMPUESTOS 1 LA CONJUNCIÓN. - Es un enunciado compuesto en el que dos proposiciones se relacionan con el conectivo “ y “, cuyo símbolo es “ ” o “ • ” (punto) y se llama conjuntor. Ejemplo: “Jorge viajó al Cusco y Luis viajó a Ica” p p : Jorge viajó al Cusco q : Luis viajó a Ica q Simbología: “p q” NOTA: También equivalen al conectivo conjunción las palabras pero, sin embargo, aunque, además, no obstante, etc.

MÁS EJEMPLOS El coche enciende cuando tiene gasolina en el tanque y tiene corriente la batería. Simbolizando tenemos: p: el coche enciende cuando tiene gasolina en el tanque q: tiene corriente la batería V(p) = V V(q) = V En consecuencia: V(p ˄ q) = V Otro ejemplo: 3 + 4 = 6 y 3 + 7 = 10 P: 3 + 4 = 6 V(p) = F Q: 3 + 7 = 10 V(q) = V Por consiguiente: V (p ˄ q) = F

TABLA DE VALORES DE VERDAD DE LA CONJUNCIÓN p q V V F F F La conjunción sólo es verdadera cuando las dos proposiciones son verdaderas.

LA CONJUNCIÓN TAREA Escribir 5 ejercicios de conjunción y determinar el valor de verdad de cada uno.

LA NEGACIÓN. - Es un tipo de proposición compuesta en la 2 que se afirma que algo no existe, que no es verdad, o que no es como alguien cree o afirma. Para negar una proposición se le antecede el conectivo no, o equivalentes a él, cuyo símbolo es “ ” (o “tilde”) y se llama negador. Ejemplo: p: Todo número elevado al cuadrado es positivo. Negación: No todo número elevado al cuadrado es positivo. p Nota: Cuando se niega una proposición compuesta, se niega al operador de mayor jerarquía en dicha proposición. Ejemplo: No es cierto que Pablo fue al banco y retiró el dinero. q Simbología: ( q r ) r

PALABRAS O FRASES QUE SE PUEDEN USAR PARA NEGAR § No… § No es cierto que § Es falso que § No es el caso que § …

TABLA DE VALORES DE VERDAD DE LA NEGACIÓN p p V F F V

3 a LA DISYUNCIÓN INCLUSIVA O DÉBIL. Es un enunciado compuesto en el que dos proposiciones se relacionan con el conectivo “ o “, cuyo símbolo es “ ” (conocido como “cuña”) y se llama disyuntor débil. Ejemplo: “Eliana viajará a Baños o a Loja”. r r : Eliana viajará a Baños. s : Eliana viajará a Loja. s Simbología: “r s” Nota: A la disyunción también se la conoce como “alternancia”. Y a los dos enunciados componentes combinados se les llama “disyuntos” o “alternativas”.

CARACTERÍSTICA DE LA DISYUNCIÓN DÉBIL O INCLUSIVA La “o” es ambigua: Tiene dos significados relacionados pero distinguibles. Ejemplo: Los recargos se cancelarán en caso de enfermedad o desempleo. Intención: a. Los recargos se cancelan para los enfermos. b. Los recargos se cancelan para los desempleados. c. Los recargos se cancelan para los enfermos y desempleados. Nota 1: La “o” inclusiva tiene el sentido de “cualquiera, posiblemente ambos”. Nota 2: La disyunción inclusiva de dos enunciados se interpreta como una aseveración de que al menos uno de los enunciados es verdadero.

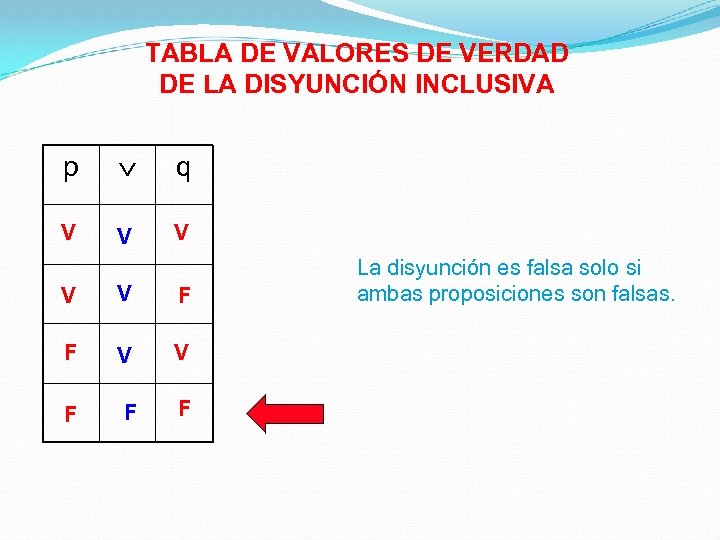TABLA DE VALORES DE VERDAD DE LA DISYUNCIÓN INCLUSIVA p q V V V F F F La disyunción es falsa solo si ambas proposiciones son falsas.

3 b LA DISYUNCIÓN EXCLUSIVA O FUERTE. Es un enunciado compuesto en el que dos proposiciones se relacionan con el conectivo “O…. . o……. “, cuyo símbolo es “ ” (Copi y Cohen usan el mismo símbolo de la disyunción inclusiva) y se llama disyuntor fuerte. Ejemplo: “O Ricardo radica en Miraflores o en La Letamendi”. p p : Ricardo radica en Miraflores. q Simbología: “p q ” q : Ricardo radica en La Letamendi. Nota 1: La disyunción excluyente se interpreta como una aseveración de que al menos uno de los enunciados es verdadero, pero no ambos.

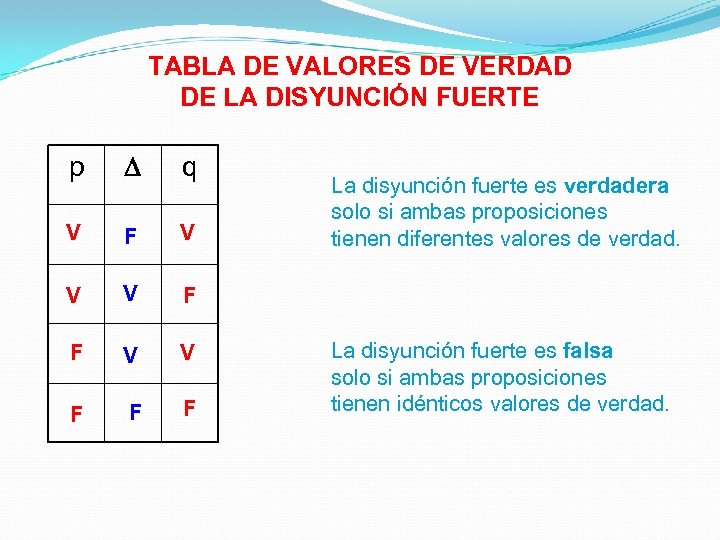TABLA DE VALORES DE VERDAD DE LA DISYUNCIÓN FUERTE p q V F V V V F F F La disyunción fuerte es verdadera solo si ambas proposiciones tienen diferentes valores de verdad. La disyunción fuerte es falsa solo si ambas proposiciones tienen idénticos valores de verdad.

¿CÓMO SE CARACTERIZA LA FORMA DEL SIGUIENTE SILOGISMO? El prisionero ciego tiene un sombrero rojo o el prisionero ciego tiene un sombrero blanco. El prisionero ciego no tiene un sombrero rojo. Por tanto, el prisionero ciego tiene un sombrero blanco. Su forma se caracteriza diciendo que su primera premisa es una disyunción, su segunda premisa es la negación del primer disyunto de la primera premisa y su conclusión es igual al segundo disyunto de la primera premisa.

LA DISYUNCIÓN INCULSIVA VS. LA EXCLUSIVA Sugerencias: - Tratar a cualquier ocurrencia de la palabra “o” como inclusiva. - Si se enuncia explícitamente que la disyunción pretende ser excluyente, se lo puede hacer añadiendo “pero no ambos”. - Cuando ambos disyuntos tienen el mismo término sujeto o el mismo término predicado, es natural condensar la formulación. Ej. : “O él es el dueño o él es el gerente” puede enunciarse: - “Él es el o el dueño o el gerente. Ej. : “O María es culpable o Mario es culpable” puede ser: - “O María o Mario son culpables”.

LA FRASE “A MENOS QUE” Se utiliza “a menos que” para formar la disyunción de dos enunciados. Ej. : “Saldrás mal en el examen a menos que estudies” se simboliza correctamente como: M ˅ E. La razón es que se utiliza “a menos que” para significar que si una proposición no es verdadera, la otra es o será verdadera. La oración puede entenderse que significa: “Si no estudias, saldrás mal en el examen”. Esa es la fuerza de la disyunción: asevera que uno de los disyuntos es verdadero y, por tanto, que si uno de ellos es falso, el otro tiene que ser verdadero.

LA PUNTUACIÓN La puntuación elimina la ambigüedad en el significado. Es decir, la puntuación establece toda la diferencia entre la verdad y la falsedad, pues diferentes puntuaciones pueden asignar diferentes valores de verdad al enunciado ambiguo. ( ) para agrupar símbolos individuales [ ] para agrupar expresiones que incluyen paréntesis { } para agrupar expresiones que incluyen corchetes

EJERCICIO DE PUNTUACIÓN Indicación: Coloque la palabra “o” para resolver la ambigüedad en la siguiente oración y a continuación use el lenguaje simbólico para caracterizarla: La organización se reunirá el jueves y José será electo o la elección será pospuesta. (p. 372)

LA NEGACIÓN DE UNA DISYUNCIÓN Se una la frase “ni… ni”. Ejemplo: “O José o Mario fue mi amigo” puede contradecirse con el enunciado: “Ni José ni Mario fue mi amigo”. La disyunción se simbolizaría como F ˅ H y su negación como ~(F ˅ H) o como (~F) • (~H). Nota: Negar que una disyunción que indica que uno u otro enunciado es verdadero requiere que se indique ambos son falsos.

LA TABLA DEL VALOR DE VERDAD DE NEGACIÓN DE UNA DISYUNCIÓN (DISYUNCIÓN NEGATIVA) p q V V F F V F (p q) F F F V

LA PALABRA “AMBOS” Surge significados diferentes cuando se coloca la palabra “ambos” en un lugar diferente en la oración. Ejemplo: - Cynthia y Jonathan ambos no serán electos. - Cynthia y Jonathan no serán electos ambos. Ejercicio: Simbolizar los enunciados. (p. 373) Nota: Con solo cambiar la posición de las palabras “ambos” y “no” se altera la fuerza lógica de lo que se asevera.

NOTAS SOBRE LA PUNTUACIÓN - Hasta aquí hemos visto tres símbolos: el punto ( • (˄)), la tilde (~) y la cuña (˅). - El símbolo de negación (tilde) se aplica al enunciado más corto que permite la puntuación. - Para trabajar con enunciados compuestos siempre se inicia con sus componentes internos y se continúa hacia afuera. Pregunta: Si A y B son enunciados verdaderos y X y Y son enunciados falsos, ¿cómo se calcularía el valor de verdad del enunciado compuesto ~[~(A • X) • (Y ˅ B)]? (p. 374) - Si las proposiciones tienen el mismo tipo de operador o conectivo lógico, se debe colocar los paréntesis de izquierda a derecha así: - Ej. : p q r = (p q) r //// p q r s = [(p q) r ] s - Ejercicio: Simbolizar el enunciado: “Estudiaré mucho y aprobaré el examen o reprobaré”.

LA NEGACIÓN Y LA DISYUNCIÓN TAREA Ejercicios: pp. 375 -379

4 EL CONDICIONAL También conocido como “hipotético” o “enunciado implicativo”, es un enunciado compuesto en el que dos proposiciones se relacionan con el conectivo “Si. . . , entonces. . . ”, cuyo símbolo es “→” (Copi y Cohen usan el símbolo de la herradura, “Ↄ”) y se llama implicador. Ejemplo: Si 12 es un número par, entonces es divisible entre 2. p q p : 12 es un número par ………………. … (antecedente) q : 12 es un número divisible entre 2 ……(consecuente) Simbología: “p → q ” o “p Ↄ q”

Notas: 1. Existen otras formas de presentarse el condicional: p por consiguiente q; p luego q; p de manera q; etc. 2. También son expresiones condicionales q ya que p; q puesto que p; q siempre que p; q porque p; etc. Ejemplo La suma de las cifras de 426 es múltiplo de 3 por consiguiente es divisible entre 3. (antecedente) p (consecuente) q 426 es divisible entre 3 porque la suma de sus cifras es múltiplo de 3. (consecuente) q (antecedente) p La simbología para ambos casos es: p → q o p Ↄ q

Implicación Material Se refiere a la relación que puede conectar dos enunciados, el enunciado “p implica materialmente que q” es verdadero cuando p es falso o q es verdadero. La implicación material no sugiere ninguna “conexión real” entre el antecedente y el consecuente. Todo lo que afirma es que de hecho, no es el caso que el antecedente es necesariamente verdadero cuando el consecuente es falso (porque puede ser verdadero o falso). Ej: . : p: Hitler fue un genio militar. q: Yo soy Jesucristo. V(p): V V(q): F Si Hitler fue un genio militar, entonces yo soy Jesucristo.

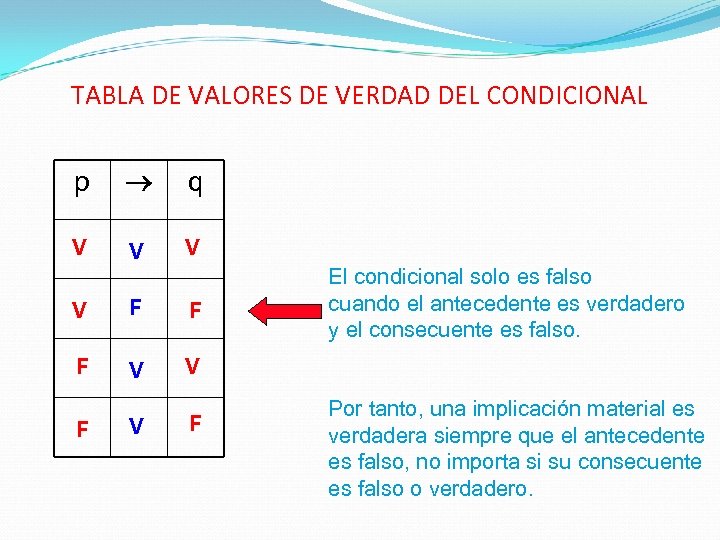TABLA DE VALORES DE VERDAD DEL CONDICIONAL p q V V F F F V V V F El condicional solo es falso cuando el antecedente es verdadero y el consecuente es falso. F Por tanto, una implicación material es verdadera siempre que el antecedente es falso, no importa si su consecuente es falso o verdadero.

EL CONDICIONAL TAREA Ejercicios de las páginas 388 -390

5. EL BICONDICIONAL Es un enunciado compuesto en el que dos proposiciones se relacionan con el conectivo “…. . …si y sólo si………. ”, cuyo símbolo es “↔” llamado doble implicador. Ejemplo: “Sicilia es una isla si y sólo si está rodeada de agua”. p p : Sicilia es una isla q : Sicilia está rodeada de agua q Simbología: p ↔q

Nota: Copi y Cohen usan la tribarra “≡” para indicar que hay una equivalencia material, esto es, que hay una relación que afirma que dos enunciados conectados por este signo tienen el mismo valor de verdad. Ej: “Iré al juego de campeonato si y sólo si puedo conseguir un boleto”. p Por tanto, mi ida al juego (p) y el que pueda conseguir un boleto (q) son materialmente equivalentes o, lo que es lo mismo, tienen la misma equivalencia material. q Simbología: p ↔q o p ≡ q

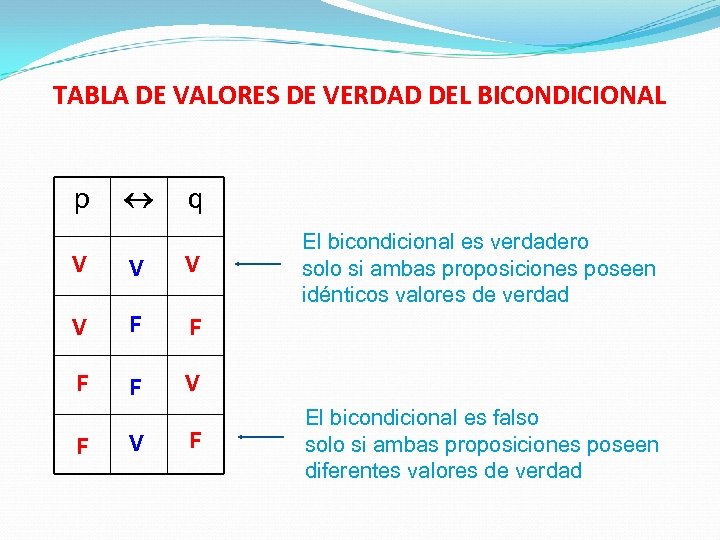TABLA DE VALORES DE VERDAD DEL BICONDICIONAL p q V V F F El bicondicional es verdadero solo si ambas proposiciones poseen idénticos valores de verdad V F El bicondicional es falso solo si ambas proposiciones poseen diferentes valores de verdad

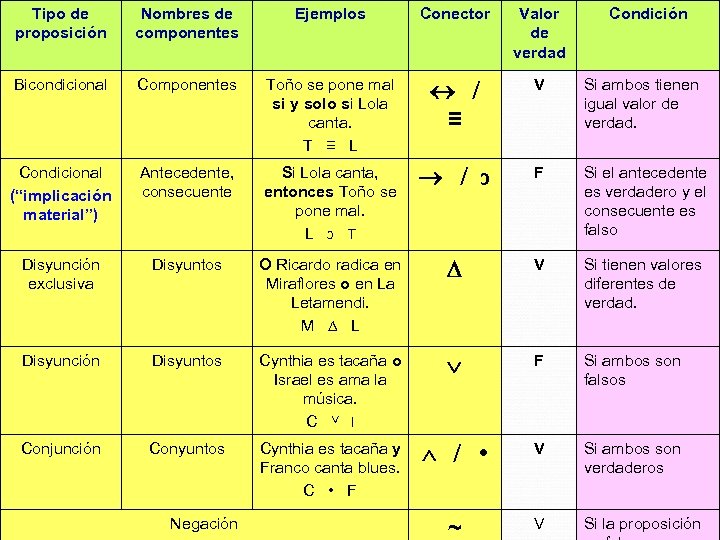Tipo de proposición Nombres de componentes Ejemplos Conector Valor de verdad Bicondicional Componentes Toño se pone mal si y solo si Lola canta. T ≡ L / ≡ V Si ambos tienen igual valor de verdad. Condicional (“implicación material”) Antecedente, consecuente Si Lola canta, entonces Toño se pone mal. L ↄ T / ↄ F Si el antecedente es verdadero y el consecuente es falso Disyunción exclusiva Disyuntos O Ricardo radica en Miraflores o en La Letamendi. M ∆ L V Si tienen valores diferentes de verdad. Disyunción Disyuntos Cynthia es tacaña o Israel es ama la música. C ˅ I F Si ambos son falsos Conjunción Conyuntos Cynthia es tacaña y Franco canta blues. C • F / • V Si ambos son verdaderos ~ V Si la proposición Negación Condición

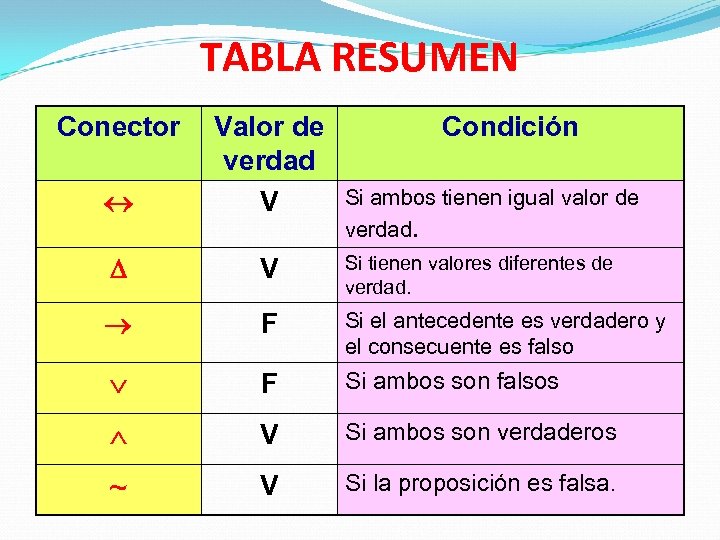TABLA RESUMEN Conector Valor de verdad V Condición V Si tienen valores diferentes de verdad. F Si el antecedente es verdadero y el consecuente es falso F Si ambos son falsos V Si ambos son verdaderos ~ V Si la proposición es falsa. Si ambos tienen igual valor de verdad.

FORMAS ENUNCIATIVAS Y EQUIVALENCIA MATERIAL La característica tabular de una fórmula lógica es la columna de valores de verdad debajo del operador de mayor jerarquía. Esta columna puede presentar los siguientes casos: 1. Cuando todos los valores de verdad son verdaderos, el esquema es una TAUTOLOGÍA. 2. Cuando todos los valores de verdad son falsos, el esquema es una CONTRADICCIÓN. 3. Cuando algunos valores de verdad son verdaderos y otros falsos el esquema es una CONTINGENCIA.