Проективная геометрия в GDI XNA докладчик Александр Каленюк

Проективная геометрия в GDI+, (XNA) докладчик: Александр Каленюк, к. т. н. по прикладной геометрии, инженерной графике, работал в Bravo Interactive, Gestalt Games. • Проективное пространство и однородные координаты. • Классы геометрических преобразований, матрицы проективных преобразований. • Группы преобразований. • Реализация геометрических преобразований в GDI+. • Нахождение матрицы преобразования по базисным точкам. • Решение задачи нахождения обратного преобразования в GDI+. • Хорошее решение нахождения матрицы обратного преобразования.

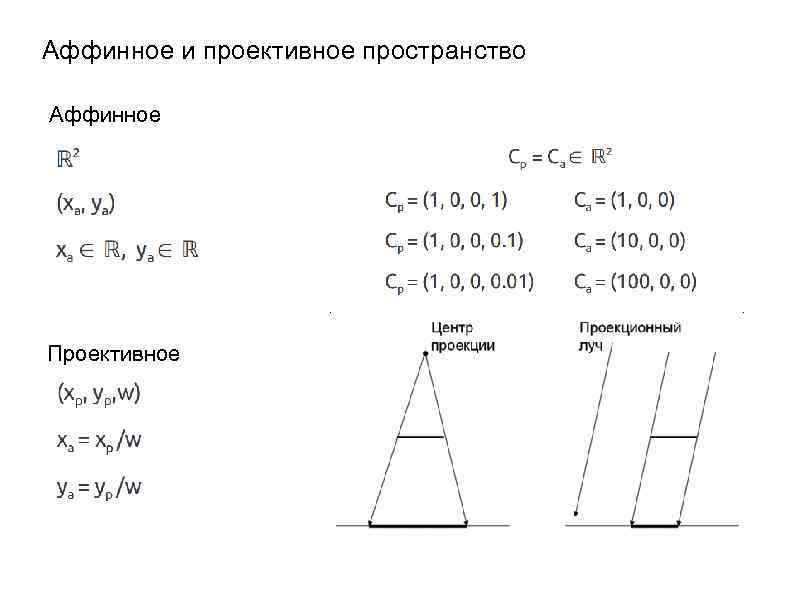Аффинное и проективное пространство Аффинное Проективное

Преобразование – это функция, которая определена на некоторой области пространства и каждой точке этой области ставит в соответствие точку из другого, или этого же самого пространства.

Проективные преобразования образуют группу. Подмножества этих преобразований образуют подгруппы. То есть группа проективных преобразований содержит в себе группу аффинных, та, в свою очередь, – группу преобразований движения. Непустое множество с заданной на нём бинарной операцией называется группой , если выполнены следующие аксиомы: ассоциативность: наличие нейтрального элемента: наличие обратного элемента: При этом проективные преобразования – не коммутативны. Повернуть и перенести – не то же самое, что и перенести и повернуть.

Нахождение матрицы прямого отображения (x'i, y'i) – это аффинные координаты углов четырехугольника (xi, yi) – это «углы» сингулярного куба: (0, 0), (0, 1), (1, 0). Множество эквивалентных преобразований: =

Нахождение матрицы обратного преобразования Это и есть сопряженная матрица. Единственное, она не разделена на определитель. Действительно, если только определитель не равен нулю, – отображение в проективном пространстве от умножения (деления) его матрицы на скаляр не поменяется.

Нахождение матрицы обратного преобразования i = 1. . 3