L-Proektir-3.ppt
- Количество слайдов: 18

Проектирование и оборудование предприятий нефтехимии (3)

1 Кинетика многостадийных реакций 1. Если механизм многостадийной реакции неизвестен, при описании ее кинетики используют формальный подход: кинетические уравнения записываются применительно к итоговому стехиометрическому уравнению AA + BB + … RR + SS + … В этом случае порядки реакции не соответствуют стехиометрическим коэффициентам и определяются экспериментально. 2. При нестационарном протекании реакции ее кинетику описывают системой дифференциальных уравнений, при стационарном – системой нелинейных алгебраических уравнений. 3. Обычно описание кинетики многостадийной реакции основывается на принятии упрощающих допущений: наличие лимитирующей стадии и квазистационарности.

2 Гетерогенно-каталитические реакции РЕАКЦИЯ: А + В продукты реакции 1. Химическая адсорбция реагентов из газовой фазы на активных центрах поверхности катализатора [K]. А + [K] [АK]; В + [K] [ВK] 2. Собственно химическая реакция на поверхности катализатора. а) адсорбционный механизм: [АK] + [ВK] [RK] + [SK] [АK] [K] + продукты реакции [АK] + [K] 2[K] + продукты реакции [АK] + [ВK] 2[K] + продукты реакции б) ударный механизм: [АK] + В [K] + продукты реакции; [BK] + A [K] + продукты реакции в) десорбция хемосорбированных продуктов: [RK] R + [K]; [SK] S + [K]

Модель идеального адсорбированного слоя 1. Адсорбция может происходить лишь на свободных активных центрах. 2. Один активный центр может адсорбировать лишь одну молекулу. 3. Все активные центры равноценны. 4. Поверхность катализатора однородна. 5. Взаимное влияние хемосорбированных молекул отсутствует. 6. Состояние катализатора неизменно. Пусть на активных центрах адсорбируются вещества A, B, R, S. N=NO+NA+NB+NR+NS N – общее количество активных центров; NO – количество свободных активных центров; NA, NB, NR, NS – соответственно количество активных центров, покрытых хемосорбированными молекулами AK, BK, RK, SK. Отнеся к N, получим: 1= O+ A+ B+ R+ S, или в общем случае: 1= O+ ∑ j 3

4 Кинетика каталитических реакций в стационарных условиях Рассмотрим мономолекулярную каталитическую реакцию А R со следующим возможным механизмом 1) А + [K] [АK]; W 1 = k 1+ A O - k 1 - A 2) [АK] [RK]; W 2 = k 2+ A - k 2 - R 3) [RK] R + [K]; W 3 = k 3+ R – k 3 - R O А R В стационарных условиях скорости последовательных реакций равны: W 1=W 2=W 3=W W = k 1+ A (1 - A- R) - k 1 - A W = k 2+ A - k 2 - R W = k 3+ R – k 3 - R (1 - A- R)

5 Лимитирующая стадия – поверхностная реакция Основное допущение: скорость каталитической реакции равна скорости поверхностной реакции, которая выражается уравнением W = W 2 = k 2+ A - k 2 - R Скорости стадий адсорбции и десорбции, находящиеся в динамическом равновесии, равны нулю. Тогда W 1 = k 1+ A О - k 1 - A=0 или k 1+ A О = k 1 - A Следовательно: A= (k 1+/ k 1 -) A О = b. A A О, где b. A= k 1+/ k 1 Аналогично: W 3 = k 3+ R – k 3 - R О =0; R= (k 3 -/ k 3+) R О = b. R R О, где b. R= k 3 -/ k 3+ Где b. A и b. R – адсорбционные коэффициенты (константы равновесия адсорбции). Подставив значения А и R в уравнение 1= O+ ∑ j, получим: O=1/(1+ b. А А+ b. R R) Подставим выражение для O в уравнение W = W 2. Тогда: W = W 2=k 2+ [b. А А-(b. R R/К 2)]/(1+ b. А А+ b. R R), где К 2= k 2+/ k 2 Для необратимой реакции: W = W 2=k 2+ b. А А/(1+ b. А А+ b. R R)
![6 Рассмотрим другой механизм реакции: 1) А + [K] [АK]; W 1 = k 6 Рассмотрим другой механизм реакции: 1) А + [K] [АK]; W 1 = k](https://present5.com/presentation/146109693_335156076/image-7.jpg)
6 Рассмотрим другой механизм реакции: 1) А + [K] [АK]; W 1 = k 1+ A O - k 1 - A 2) [АK] + [K] [RK] + [K]; W 2 = (k 2+ A - k 2 - R) О 3) [RK] R + [K]; W 3 = k 3+ R – k 3 - R O А R Тогда для обратимой реакции: W = W 2=k 2+ [b. А А-(b. R R/К 2)]/(1+ b. А А+ b. R R)2 Для необратимой реакции: W = W 2=k 2+ b. А А/(1+ b. А А+ b. R R)2 Рассмотрим биномолекулярную каталитическую реакцию А+B R+S 1) А + [K] [АK]; W 1 = k 1+ A O - k 1 - A 2) B + [K] [BK]; W 2 = k 2+ B O - k 1 - B 3) [АK] [RK]; W 3 = k 3+ A – k 3 - B 4) [BK] [SK]; W 4 = k 4+ B – k 4 - S 5) [RK] R + [K]; W 5 = k 5+ R – k 5 - R O 6) [SK] S + [K]; W 6 = k 6+ S – k 6 - S O А+B R+S

7 Если лимитирующей является поверхностная реакция – стадия 3, – то кинетическое уравнение имеет вид: W = W 3=k 3+ [b. А А b. В В-(b. R R b. S S/К 3)]/(1+ b. А А+b. B B+b. R R+ b. R S) Для необратимой реакции: W = W 3=k 3+ b. А А b. В В/(1+ b. А А+b. B B+b. R R+ b. R S) Лимитирующая стадия – химическая адсорбция Основное допущение: скорость каталитической реакции равна скорости химической адсорбции, которая выражается уравнением W = W 1 = k 1+ A O - k 1 - A Скорости стадий поверхностной реакции и десорбции, находящиеся в динамическом равновесии, равны нулю: W 2 = k 2+ A - k 2 - R=0 или k 2+ A = k 2 - R W 3 = k 3+ R – k 3 - R O=0 или k 3+ R = k 3 - R O Тогда: R = b. R R O, A = R/K 2= b. R R O /K 2 Следовательно: O+ A + R=1, откуда O=/(1+b. R R + b. R R/К 2) W = W 1=k 1+ [А-(b. R R/(b. R К 2))]/(1+ b. А А+ b. R R)

8 Лимитирующая стадия –десорбция Основное допущение: скорость каталитической реакции равна скорости десорбции, которая выражается уравнением W = W 3 = k 3+ R – k 3 - R O Скорости стадий поверхностной реакции и десорбции, находящиеся в динамическом равновесии, равны нулю: Тогда W 1 = k 1+ A O - k 1 - A=0 или k 1+ А О = k 1 - А W 2 = k 2+ A - k 2 - R =0 или k 2+ A = k 2 - R Тогда: A = b. A A O, R = K 2 A = K 2 b. A A O Следовательно: O+ A + R=1, откуда O=/(1+ b. A A + К 2 b. A A) W = W 3=k 3+ [К 2 b. A A -b. R R]/(1+ b. A A + К 2 b. A A)

Допущение о квазистационарности Основное допущение: скорости образования и расходования поверхностных комплексов равны, т. е. d[АK]/dt=W 1 -W 2=0 или k 1+ A O - k 1 - A - k 2 A =0 d[RK]/dt=W 2 -W 3=0 или k 2 A - k 3+ R + k 3 - R O =0 Отсюда следует, что все скорости равны: W 1=W 2 =W 3= W. Для простоты предположим, что поверхностная реакция W 2 необратима. Тогда с учетом O = 1 - A - R получим два уравнения с двумя неизвестными ( A и R). Решив эту систему уравнений, найдем: и W=k 2 A Если поверхностная реакция лимитирующая, т. е. k 2 гораздо меньше всех остальных констант, то выражение для А упрощается: 9

10 Анализ кинетических моделей химических реакций 1. Термодинамический анализ Задачи термодинамического анализа: 1. Определение возможности самопроизвольного протекания реакции в данном направлении. 2. Определение предела самопроизвольного протекания реакции, т. е. состояния химического равновесия. 3. Расчет теплового эффекта реакции. Основной характеристикой химического равновесия является константа равновесия. Для реакции типа AA + BB RR + SS константа равновесия определяется из условия равенства скоростей прямой и обратной реакций: Тогда
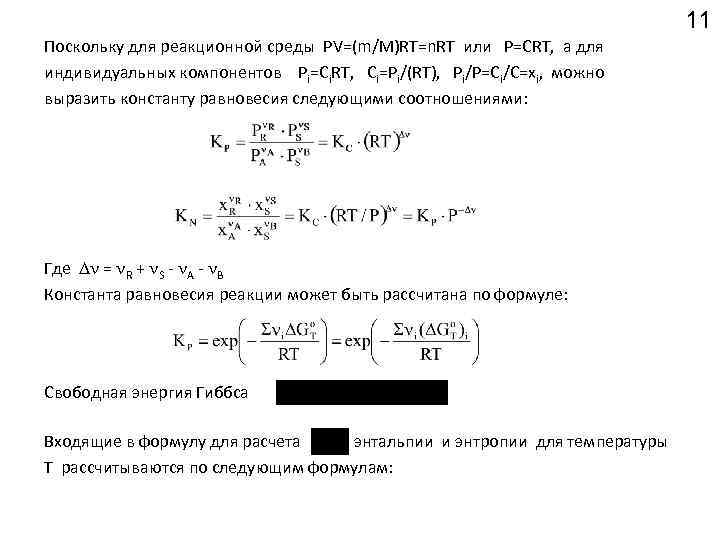
11 Поскольку для реакционной среды РV=(m/M)RT=n. RT или P=CRT, а для индивидуальных компонентов Pi=Ci. RT, Ci=Pi/(RT), Pi/P=Ci/C=xi, можно выразить константу равновесия следующими соотношениями: Где = R + S - A - B Константа равновесия реакции может быть рассчитана по формуле: Свободная энергия Гиббса Входящие в формулу для расчета энтальпии и энтропии для температуры Т рассчитываются по следующим формулам:

12 где Т=Т-298, = Т /1000. Мольные теплоемкости компонентов для температуры Т рассчитываются по формуле: Сpi=ai+bi(T/1000)+ci(T/1000)2+di(T/1000)3 Средняя теплоемкость реакционной смеси состава хi равна: Cр= хi. Cpi. Все теплофизические параметры (a, b, c и d для теплоемкости, G, H и S) рассчитываются на основе некоторых групповых составляющих (структурных энергетических фрагментов) по известным методикам. Если стандартные значения ( Gо 298 , Hо 298 и Sо 298) для молекул определены экспериментально, то их расчет не проводится.

13 Две задачи, решаемые при анализе состояния химического равновесия: 1. Расчет состава равновесной реакционной среды. 2. Определение влияния на равновесный состав параметров реакции: температура, давление, начальный мольный состав реагентов, содержание инертных компонентов и/или продуктов реакции. Для примера рассмотрим реакцию 2 A R+S с условием Ао=1. Для нее =0, т. е. KP=KN. Пусть у – степень превращение компонента А. Тогда ХА=1 -у, а из стехиометрии реакции XR=XS=y/2, т. е. КР=(у/2)2/(1 -у)2=у2/(1 -у)2/4 или у=2(КР)1/2/[1+2(КР)1/2] Уравнения влияния температуры и давления на величину константы равновесия предложил Вант-Гофф: d[ln(KP)]/d. T=-QP/(RT 2) d[ln(KN)]/d. P=- V/(RT) V – изменение объема системы.

14 Из первого уравнения следует, что для экзотермических реакций (QP 0) производная всегда положительна, следовательно КР и Т изменяются в одном направлении, т. е. КР возрастает при повышении Т; для экзотермических реакций (QP>0) производная всегда отрицательна, т. е. КР и Т изменяются в разных направлениях, поэтому КР возрастает при понижении Т. Из второго уравнения следует, что для реакций, протекающих с уменьшением объема С, KN возрастает при повышении Р, а для реакций, протекающих с увеличением объема ( V >0), KN возрастает при понижении Р. Наконец, для реакций, протекающих без изменения объема ( V=0), давление на величину константы равновесия не влияет. При увеличении содержания инертных компонентов снижаются равновесный выход продуктов и равновесная степень превращения реагентов. Увеличение содержания продуктов реакции в равновесной смеси вызывает уменьшение содержания реагентов и наоборот.

15 Наблюдаемая скорость реакции Суммарная скорость реакции определяется частными процессами: переносом реагентов из потока к поверхности зерна катализатора за счет диффузии и массообменом на границе раздела зерно-поток. Скорость переноса реагента из ядра потока к внешней поверхности катализатора пропорциональна коэффициенту молекулярной диффузии D и градиенту концентраций, который можно определить как разность концентраций (Со – Cf), деленную на толщину пограничного слоя . Тогда скорость массопереноса можно записать в виде: Для необратимой реакции первого порядка А R скорость может быть выражена как Комбинируя два уравнения, найдем значения Cf и WНАБЛ в стационарных условиях

Из анализа выражения наблюдаемой скорости вытекают два частных случая. 1. о>>kf, тогда k. НАБЛ=kf, Cf=Co; WНАБЛ=kf Co; эти условия отвечают кинетической области протекания процесса. 2. о kf, тогда k. НАБЛ= о, Cf Co; WНАБЛ= о Co; эти условия отвечают диффузионной области протекания процесса. Зависимость коэффициентов массо- ( ) и теплоотдачи ( ) зависит от скорости потока и физических свойств реагента выражается следующими полуэмпирическими критериальными уравнениями: Где Sh – критерий Шервуда; Re=UL/ - критерий Рейнольдса; Sс= /D – критерий Шмидта; D – коэффициент диффузии, м 2/с ; А – коэффициент пропорциональности; n, m – эмпирические показатели степеней; U – скорость потока, м/с; L – характерный линейный размер, м; – коэффициент кинематической вязкости, м 2/с; – плотность потока, кг/м 3. 16

7
L-Proektir-3.ppt