Проект Математика царица всех Наук Цель

Проект Математика – царица всех Наук

Цель Определить связь математики с другими предметами.

Математика – царица наук Есть о математике молва, Что она в порядок ум приводит. Потому хорошие слова Часто говорят о ней в народе.

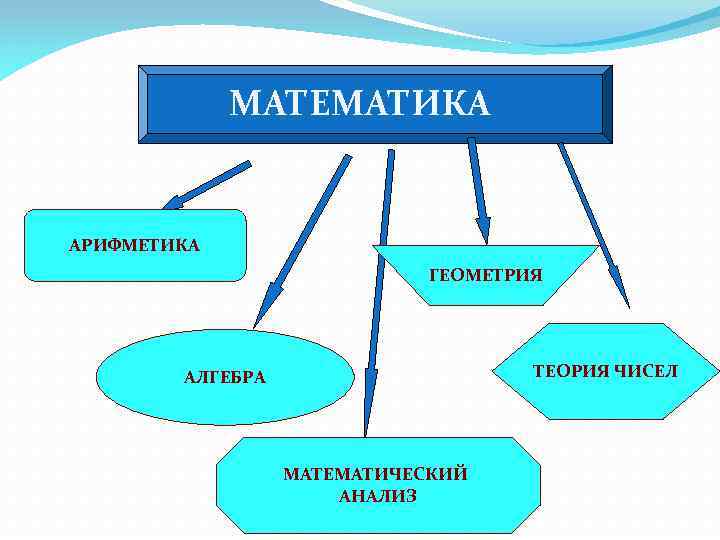МАТЕМАТИКА АРИФМЕТИКА ГЕОМЕТРИЯ ТЕОРИЯ ЧИСЕЛ АЛГЕБРА МАТЕМАТИЧЕСКИЙ АНАЛИЗ

История математики

1. Кто из них сказал: «Математика – царица всех наук, а арифметика – царица математики» ?

Карл Фридрих Гаусс – «король арифметики» • Карл Гаусс (1777 – 1855) • Немецкий математик, астроном, физик, геодезист. • Выдающиеся математические способности обнаружил в раннем детстве. • Его многочисленные исследования в области математики оказали серьезное влияние на развитие других наук.

2. Кому принадлежат эти строки: «Математику уже затем учить надо, что она ум в порядок приводит» ?

Михаил Васильевич Ломоносов • Михаил Васильевич Ломоносов (1711 – 1765) • - великий ученый: химик, физик, математик, поэт, основатель российской науки, Московского Государственного Университета.

Вектор в физике и математике С понятием «вектор» учащиеся знакомятся на уроках геометрии на примере параллельного переноса. Представление о направленном отрезке позволяет перейти к введению физических векторных величин, которые так же, как и параллельный перенос, изображаются направленными отрезками. Наиболее подходящей величиной для введения векторов и операций над ними является перемещение с его «естественным» правилом сложения. . Перемещение в физике представляет собой более узкое понятие. Вектор перемещения вводится при рассмотрении движения материальной точки или поступательного движения твёрдого тела. При таком движении все точки тела движутся одинаково. Перемещению при поступательном движении тела в механике соответствует параллельный перенос в геометрии. Следовательно, перемещение есть не что иное, как геометрический вектор. На уроках физики следует обратить внимание на понятие проекции вектора, теорему о проекциях, формулу. Для физиков важен распределительный закон , поскольку знание его позволяет сделать важный вывод о том, что работа результирующей силы равна сумме работ составляющих сил.

Связь географии и математики При изучении темы "Атмосфера" очень тесной является связь географии с математикой. Данная тема включает такие понятия, как температура, атмосферное давление, влажность, осадки, ветер. В математике рассматриваются столбчатые и круговые диаграммы, вычисляют среднее арифметическое, читают графики. И все это как нельзя, кстати, для получения среднемесячной, среднегодовой температур воздуха, а для вычисления расстояния между двумя точками координатной оси нахождения амплитуды температуры воздуха. Ребята учатся отвечать на вопросы, используя графики зависимости температуры от времени года, от высоты. Определяют преобладающее направление ветра по графику розы ветров. Чтобы увидеть наглядное представление о количестве осадков в течение года и по месяцам, строят столбчатые и круговые диаграммы. На уроках темы "Реки России" при знакомстве с типами водного режима рек одновременно закрепляются знания по теме "Функции. Свойства функций" из математики. Поскольку тип водного режима определяется по распределению расхода воды в течении года. Графики распределения расхода воды ничто иное, как графики функций. График функции это не нечто абстрактное, существующее само по себе, и необходимое звено для составления прогнозов наводнений, что без знания математики нельзя провести какое либо водохозяйственное мероприятие, будь то орошение, водоснабжение, осушение, строительство гидроэлектростанции, сооружение водохранилища.

Связь математики и химии может осуществляться в различных направлениях. К основным из них можно отнести широкое использование в учебном процессе математической символики, использование математических подходов к объяснению химического материала, выявление функциональных отношений между величинами, поиск математической формы выражения химических концепций и др. Одним из центральных пунктов связи химии и математики является выявление функциональных отношений между величинами. Функциональная зависимость должна пронизывать курс химии, способствуя развитию у учащихся математического мышления. Курс химии имеет большое количество функционально связанных между собой величин. Вскрытие этих связей поможет установлению действенных связей химии и математики. Так, при изучении химии эффективно может быть использована прямая пропорциональная зависимость y=kx. Это, например, связь между величинами массы и числом молей вещества, между количеством вещества и тепловой энергией, выделившейся или поглотившейся в результате химической реакции, и др. Обратная пропорциональность у - выражает связь между массой раствора и его концентрацией при разбавлении или упаривании раствора. При решении химических задач надо опираться на имеющиеся у учащихся знания функциональных отношений, воспитывая умение изображать химическую идею в математическом виде. Наиболее часто на занятиях по химии употребляются умения учащихся производить простейшие расчеты с использованием понятий процента, пропорции, уравнения. Кроме этого, в старших классах целесообразно применять знания о функциональной зависимости величин, графике, отражающем эту зависимость, а также знания из курса геометрии. Таким образом, для успешного использования на уроках химии понятий «процент» и «пропорция» имеются необходимые условия. Необходимо лишь кратко повторить математическую сущность этих понятий, а затем осуществить перенос их на химическое содержание. Кроме алгебры, на уроках химии используются знания учащихся по геометрии. Учащимся приходится применять некоторые геометрические представления для расчета углов между химическими связями, определения пространственной конфигурации простейших молекул. Уже при изучении метана возникает необходимость показать, что его молекула имеет тетраэдрическую форму. Решение данной задачи можно произвести на основе знаний учащихся свойств правильных треугольников и пирамиды. В процессе нахождения углов между связями С — Н учащиеся воспользуются теоремой синусов. Использовать математические знания школьников можно в процессе изготовления пространственных моделей молекул. Например, если требуется построить модель молекулы метана, то необходимо на основе радиуса шара определить длину ребра вписанного в него тетраэдра. При решении этой задачи учащиеся должны применить знания не только по геометрии, но и по тригонометрии. Знания основ геометрии и векторной алгебры могут помочь при определении степени полярности молекул простейших соединений. Например, можно определить дипольный момент воды, если известей дипольный момент связи О — Н и угол между связями. Для этого учащиеся строят параллелограмм векторов, а затем пользуются теоремой синусов. Решая подобную задачу относительно углекислого газа, они приходят к выводу, что молекула оксида углерода (IV) не полярна. Использование межпредметных связей с математикой позволяет учащимся глубже понять вопросы химии, представить с определенной степенью наглядности структуры атомов и молекул. Применение математики стимулирует процесс познания химических явлений, направляет учащихся на поиск новых решений. Все это открывает большие возможности успешного развития учащихся, привития им навыков самостоятельно добывать знания.

Связь биологии и математики Биология широко использует математический аппарат при проведении тех или иных исследований. Например, ежегодно ученики нашей школы пишут исследовательские работы по биологической и экологической проблематике (например, «Социологическое исследование экологического сознания жителей Санкт Петербурга» , «Разработка проекта очистки воды в реке Оккервиль» , «Возрастные различия в переключении произвольного внимания у детей и подростков» и др. ) Любое исследование предполагает статистическую обработку результатов: ранжирование, построение графиков и диаграмм, подсчёт среднего арифметического, среднеквадратичного отклонения, процентной доли, коэффициентов корреляции. При изучении генетических законов, решении задач по генетике, биохимии и популяционной генетике математический аппарат необходим как при освоении теоретического материала, так и при решении конкретных задач. На протяжении многих лет в школе действует факультатив, рассматривающий золотое сечение в природе. Организация занятий такова, что обучающимся предоставляется широкая возможность самостоятельной работы при подборе материала, подготовке сообщений и презентаций. Хотя занятия на факультативе проводит учитель математики, учителя других профилей не только принимают в них участие, но и на своих уроках используют материал этого курса. В частности, на уроках ботаники мы обращаем внимание на то, что очередное листорасположение подчиняется правилу золотого сечения: дробь, числитель которой — это число оборотов на стебле, а знаменатель — число листьев в цикле, соответствует рядам Фибоначчи, например, 3/8 или 5/13. Подобную же логарифмическую спираль можно обнаружить в расположении семян в корзинках сложноцветных, чешуй — в шишках голосеменных, колючек на стебле кактусов. Во всех этих случаях спирали заворачиваются навстречу другу, а число правых и левых спиралей всегда относится друг к другу как соседние числа в ряду Фибоначчи. Переходя к курсу зоологии, мы вновь сталкиваемся с логарифмической спиралью в строении раковины моллюска. По законам золотого сечения построены тела бабочек, стрекоз и ящериц, этому же правилу подчиняется форма яиц птиц. Та же логарифмическая спираль обнаруживается и в строении костного лабиринта (улитки) внутреннего уха. Золотую пропорцию можно обнаружить в строении человеческого тела и в чертах лица. Но те только в анатомии можно увидеть золотую пропорцию. Отношение продолжительности систолы и диастолы сердечного цикла также составляет дробь из соседних чисел ряда Фибоначчи. Чем больше сердечный ритм отклоняется от идеальной частоты, тем больше энергетические затраты организма и тем ниже эффективность работы сердца.

Задачи

Физкультура На соревнованиях по бегу было 4 участника Вася, Федя, Дима и Лёша. За сколько часов они пробегут 1 километр если: Ваня пробегает 100 метров за 8, 2 секунды, Федя за 8, 1 секунду, Дима за 8, 5 секунд, а Лёша за 8, 8 секунд? Решение: В 1 км – 1000 м. 8, 2*10=82(мин) – пробежал 1 км Вася. 8, 1*10=81(мин) – пробежал 1 км Федя. 8, 5*10=85(мин) – пробежал 1 км Дима. 8, 8*10=88(мин) – Пробежал 1 км Лёша. В 1 часе 60 мин => 82 мин – 1, 22 ч ; 81 мин – 1, 21 ч; 85 мин – 1, 25 ч; 88 мин – 1, 28 ч. Ответ: Вася пробежал за 1, 22; Федя за 1, 21; Дима за 1, 25 ч; Лёша за 1, 28 ч.

Химия

Физика На рисунке представлена вольт амперная характеристика металлического проводника. Воспользовавшись рисунком определите сопротивление проводника.

Фонарь массой М = 10 кг подвешен над серединой улицы шириной L = 10 м на канатике, допустимая сила натяжения которого Т = 500 Н. Определить высоту Н крепления концов канатика, если точка крепления фонаря должна находиться на высоте h = 5 м? Дано: М = 10 кг, L = 10 м, Т = 500 Н, h = 5 м. Определить Н - ? Для решения задачи нарисуем рисунок. На фонарь действуют силы: Mg - сила тяжести и силы натяжения канатиков Т 1 и Т 2. Так как фонарь находится в состоянии равновесия, то, применяя первый закон Ньютона, запишем векторное уравнение равновесия: Mg + Т 1 + Т 2 =0. Спроецируем это уравнение на оси OX и OY: OX: Т 2 sinα - Т 1 sinα = 0 (1), OY: Т 1 cosα + Т 2 cosα – Mg = 0 (2). Из уравнения (1) получаем, что Т 1 = Т 2 (это очевидно из условия задачи). Тогда выразим силы натяжения канатиков через Т = Т 1 = Т 2. Из уравнения (2) получим 2 Т cosα = Mg, откуда cosα = Mg/2 Т (3). В задаче нам надо определить высоту подвеса крепления канатиков фонаря Н (точка С), которую мы найдем из выражения Н = h + d , следовательно надо найти расстояние d. Величину d можно определить из прямоугольного треугольника ΔОАС. В треугольнике катеты АС = L/2, АО= d и гипотенуза ОС = √d² + L²/4. Тогда cosα = АО/ ОС = d/ √d² + L²/4. Подставляем полученное выражение в (3) и определяем d:

География Какое местное время в Запорожье, если в Киеве местное время 13 часов? Решение: Определяем по карте долготу г. Киева и г. Запорожья. Долгота г. Киева долгота г. Запорожья в. д. 1. Находим разницу долгот: 2. Переводим градусы в минуты и находим разницу во времени через угловую скорость Земли, т. е. 3. Зная разницу во времени 18' 24" между городами, находим мест ное время Запорожья: Ответ: Местное время в Запорожье будет 13 часов 18 минут 24 секунды, т. к. г. Запорожье расположено восточнее Киева на .

Вывод Выполняя этот проект мы убедились в том что математика действительно царица всех наук и без знаний математики не возможно решить ни одну задачу по другим школьным предметам.

Подготовили: Александр Сивохин и Артём Бурченко.

Источники http: //shools geograf. at. ua/load/zadachi_po_geografii/opredelenie_vremeni_2/51 1 0 365 http: //ru. wikipedia. org/wiki/%D 0%97%D 0%B 0%D 0%B 3%D 0%BB%D 0%B 0%D 0%B 2%D 0%BD%D 0 %B 0%D 1%8 F_%D 1%81%D 1%82%D 1%80%D 0%BD%D 0%B 8%D 1%86%D 0%B 0 Учебник по Химии. Учебник по Физике.

СПАСИБО ЗА ВНИМАНИЕ!