f7875567d7b95328e9f4d4f6c2dbb319.ppt
- Количество слайдов: 139
 Produits Structurés Actions
Produits Structurés Actions
 Sommaire 1ère Partie: Ingénierie Financière 2ème Partie: Organisation d’une salle des marchés 3ème Partie: Description des produits structurés 4ème partie: Trading 5ème partie: Eléments de pricing Etude de cas n° 1 : BMTN indexé sur CAC 40 Etude de cas n° 2: BLAC
Sommaire 1ère Partie: Ingénierie Financière 2ème Partie: Organisation d’une salle des marchés 3ème Partie: Description des produits structurés 4ème partie: Trading 5ème partie: Eléments de pricing Etude de cas n° 1 : BMTN indexé sur CAC 40 Etude de cas n° 2: BLAC
 Produits Structurés Actions 1ère Partie : Ingénierie Financière
Produits Structurés Actions 1ère Partie : Ingénierie Financière
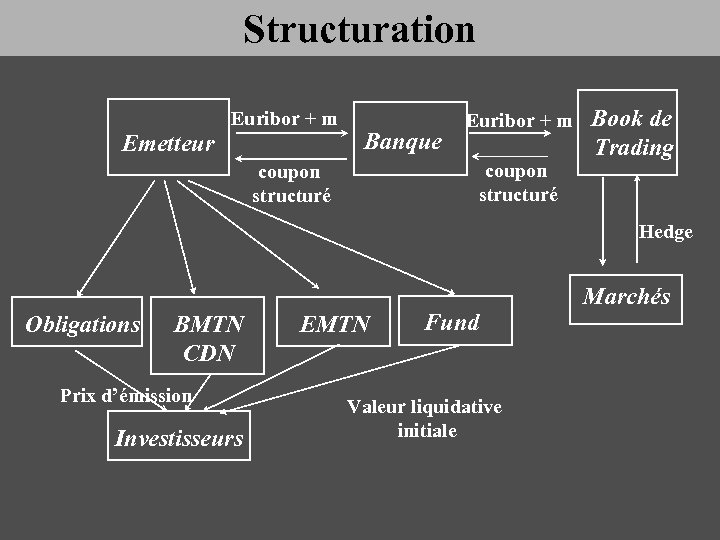 Structuration Euribor + m Emetteur Banque Euribor + m coupon structuré Book de Trading Hedge Obligations BMTN CDN Prix d’émission Investisseurs EMTN Fund Valeur liquidative initiale Marchés
Structuration Euribor + m Emetteur Banque Euribor + m coupon structuré Book de Trading Hedge Obligations BMTN CDN Prix d’émission Investisseurs EMTN Fund Valeur liquidative initiale Marchés
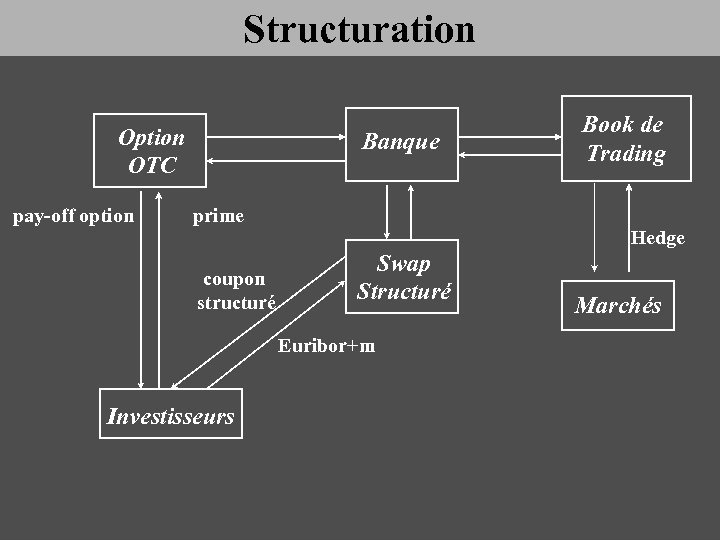 Structuration Option OTC pay-off option Banque prime coupon structuré Hedge Swap Structuré Euribor+m Investisseurs Book de Trading Marchés
Structuration Option OTC pay-off option Banque prime coupon structuré Hedge Swap Structuré Euribor+m Investisseurs Book de Trading Marchés
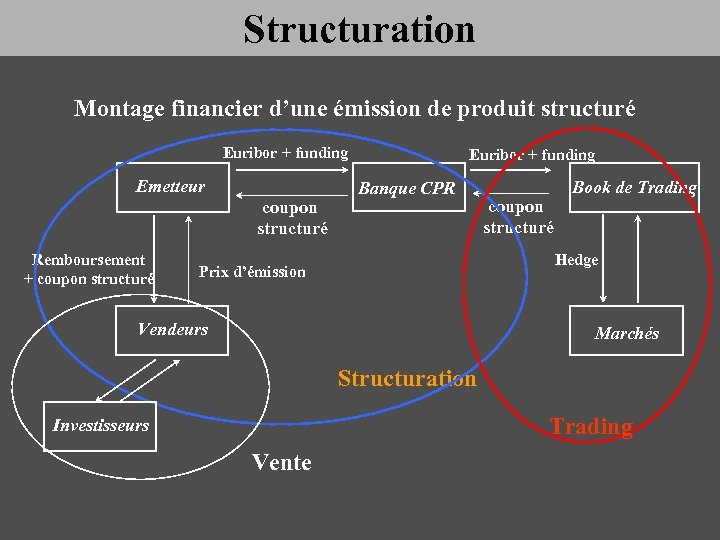 Structuration Montage financier d’une émission de produit structuré Euribor + funding Emetteur coupon structuré Remboursement + coupon structuré Euribor + funding Banque CPR coupon structuré Book de Trading Hedge Prix d’émission Vendeurs Marchés Structuration Trading Investisseurs Vente
Structuration Montage financier d’une émission de produit structuré Euribor + funding Emetteur coupon structuré Remboursement + coupon structuré Euribor + funding Banque CPR coupon structuré Book de Trading Hedge Prix d’émission Vendeurs Marchés Structuration Trading Investisseurs Vente
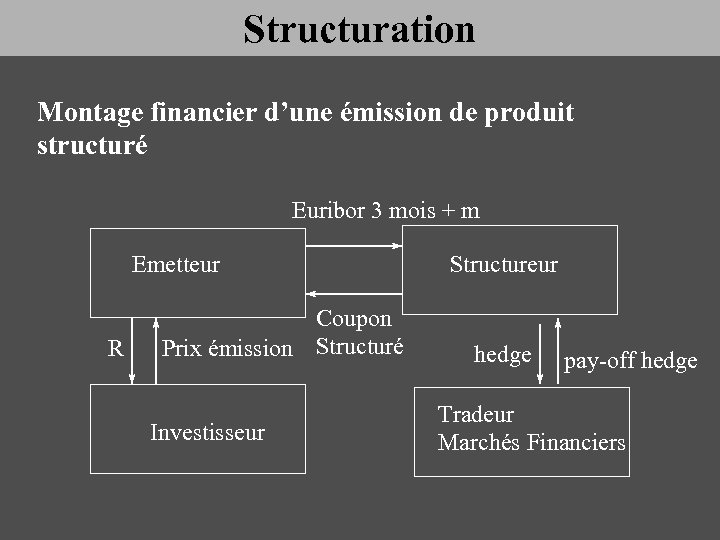 Structuration Montage financier d’une émission de produit structuré Euribor 3 mois + m Emetteur R Coupon Prix émission Structuré Investisseur Structureur hedge pay-off hedge Tradeur Marchés Financiers
Structuration Montage financier d’une émission de produit structuré Euribor 3 mois + m Emetteur R Coupon Prix émission Structuré Investisseur Structureur hedge pay-off hedge Tradeur Marchés Financiers
 Produits Structurés Actions 2ème Partie : organisation d’une salle des marchés
Produits Structurés Actions 2ème Partie : organisation d’une salle des marchés
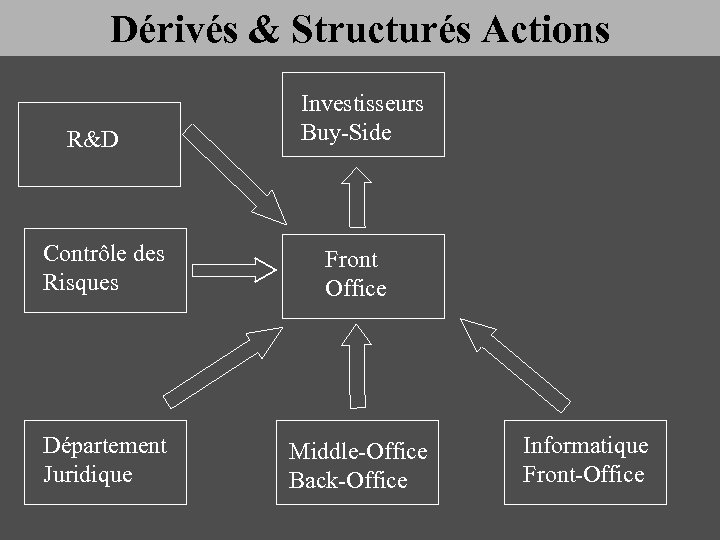 Dérivés & Structurés Actions R&D Investisseurs Buy-Side Contrôle des Risques Front Office Département Juridique Middle-Office Back-Office Informatique Front-Office
Dérivés & Structurés Actions R&D Investisseurs Buy-Side Contrôle des Risques Front Office Département Juridique Middle-Office Back-Office Informatique Front-Office
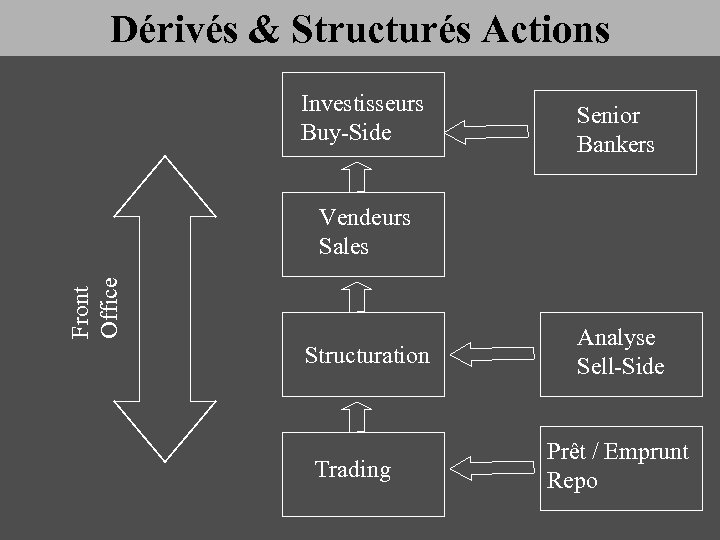 Dérivés & Structurés Actions Investisseurs Buy-Side Senior Bankers Front Office Vendeurs Sales Structuration Trading Analyse Sell-Side Prêt / Emprunt Repo
Dérivés & Structurés Actions Investisseurs Buy-Side Senior Bankers Front Office Vendeurs Sales Structuration Trading Analyse Sell-Side Prêt / Emprunt Repo
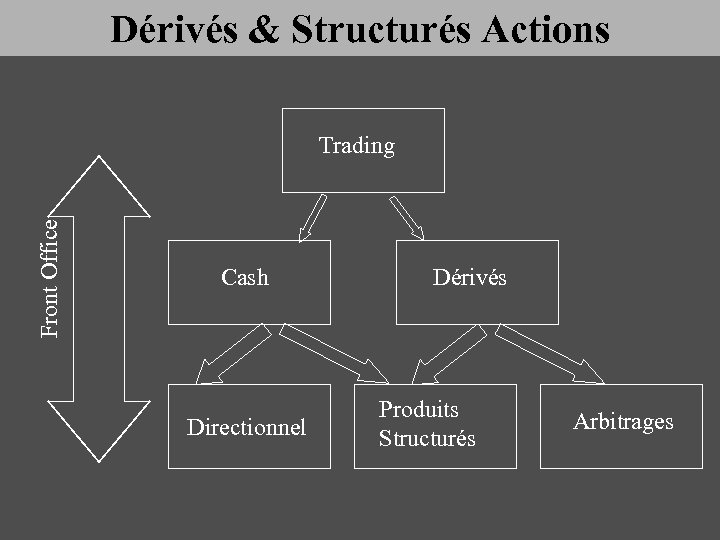 Dérivés & Structurés Actions Front Office Trading Cash Directionnel Dérivés Produits Structurés Arbitrages
Dérivés & Structurés Actions Front Office Trading Cash Directionnel Dérivés Produits Structurés Arbitrages
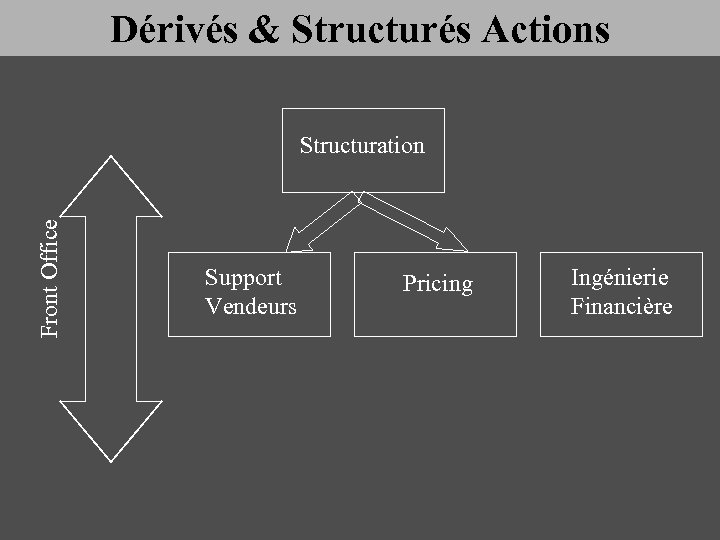 Dérivés & Structurés Actions Front Office Structuration Support Vendeurs Pricing Ingénierie Financière
Dérivés & Structurés Actions Front Office Structuration Support Vendeurs Pricing Ingénierie Financière
 Dérivés & Structurés Actions Front Office Vendeurs Sales Cash Dérivés
Dérivés & Structurés Actions Front Office Vendeurs Sales Cash Dérivés
 Dérivés & Structurés Actions Front Office Analyse Sell-Side Analyse Fondamentale Analyse Technique
Dérivés & Structurés Actions Front Office Analyse Sell-Side Analyse Fondamentale Analyse Technique
 Dérivés & Structurés Actions SDM Contrôle des Risques Définition des limites Suivi des limites Value At Risque VAR
Dérivés & Structurés Actions SDM Contrôle des Risques Définition des limites Suivi des limites Value At Risque VAR
 Dérivés & Structurés Actions SDM Département Juridique Juristes de Marchés Fiscalistes
Dérivés & Structurés Actions SDM Département Juridique Juristes de Marchés Fiscalistes
 Dérivés & Structurés Actions SDM Informatique Front-Office Flux Financiers Développement C++
Dérivés & Structurés Actions SDM Informatique Front-Office Flux Financiers Développement C++
 Dérivés & Structurés Actions SDM R&D Recherche Quantitative Recherche Economique
Dérivés & Structurés Actions SDM R&D Recherche Quantitative Recherche Economique
 Dérivés & Structurés Actions SDM Grands Comptes Senior Banker Départements Spécialisés
Dérivés & Structurés Actions SDM Grands Comptes Senior Banker Départements Spécialisés
 Dérivés & Structurés Actions SDM Prêt Emprunt Asset Management Banques Assureurs
Dérivés & Structurés Actions SDM Prêt Emprunt Asset Management Banques Assureurs
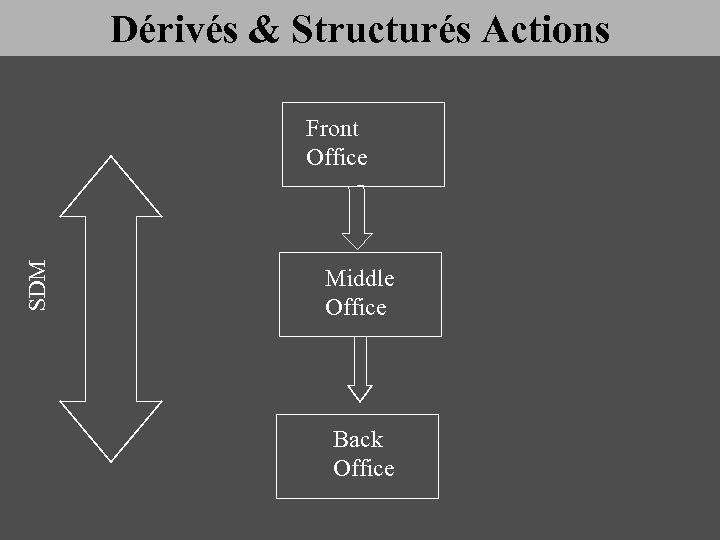 Dérivés & Structurés Actions SDM Front Office Middle Office Back Office
Dérivés & Structurés Actions SDM Front Office Middle Office Back Office
 Dérivés & Structurés Actions Investisseurs Buy-Side § Assureurs + Mutuelles § Compte propre § Actifs Réglementaires § ALM § Asset Management § OPCVM § Caisses de Retraites § Réserves § Actifs Réglementaires § ALM § Etablissements Financiers § Compte propre § ALM
Dérivés & Structurés Actions Investisseurs Buy-Side § Assureurs + Mutuelles § Compte propre § Actifs Réglementaires § ALM § Asset Management § OPCVM § Caisses de Retraites § Réserves § Actifs Réglementaires § ALM § Etablissements Financiers § Compte propre § ALM
 Dérivés & Structurés Actions Analyse Sell-Side § § § § Analyse Financière Recommandations Montages Haut de Bilan Vente (road show) SFAF IBES § Analyse Buy-Side § Investisseurs Institutionnels
Dérivés & Structurés Actions Analyse Sell-Side § § § § Analyse Financière Recommandations Montages Haut de Bilan Vente (road show) SFAF IBES § Analyse Buy-Side § Investisseurs Institutionnels
 Dérivés & Structurés Actions Middle-Office Back-Office § Middle-Office § Analyse des tickets § Suivi des résultats et reporting § Back-Office § § Saisie des tickets Edition des confirmations Règlement / Livraison Clearing (Clearstream + Euroclear + Sicovam)
Dérivés & Structurés Actions Middle-Office Back-Office § Middle-Office § Analyse des tickets § Suivi des résultats et reporting § Back-Office § § Saisie des tickets Edition des confirmations Règlement / Livraison Clearing (Clearstream + Euroclear + Sicovam)
 Dérivés & Structurés Actions Contrôle des Risques § Contrôle des Risques de Marchés § § § Définition des facteurs de risques de marchés Modélisation des facteurs de risques Mesure et suivi des facteurs de risques Définition des limites (affectation des fonds propres) Respect des limites par les Tradeurs Analyse du P&L (volatilité, rentabilité, ROE)
Dérivés & Structurés Actions Contrôle des Risques § Contrôle des Risques de Marchés § § § Définition des facteurs de risques de marchés Modélisation des facteurs de risques Mesure et suivi des facteurs de risques Définition des limites (affectation des fonds propres) Respect des limites par les Tradeurs Analyse du P&L (volatilité, rentabilité, ROE)
 Dérivés & Structurés Actions Contrôle des Risques § Contrôle des Risques de Marchés § Calcul de la Value At Risque (VAR) Si VAR 1 Y 99% = 100 millions € alors le « Book » de trading a une probabilité de 1% de perdre 100 millions € au cours d’une année
Dérivés & Structurés Actions Contrôle des Risques § Contrôle des Risques de Marchés § Calcul de la Value At Risque (VAR) Si VAR 1 Y 99% = 100 millions € alors le « Book » de trading a une probabilité de 1% de perdre 100 millions € au cours d’une année
 Dérivés & Structurés Actions Informatique Front-Office § Informatique Front-Office / Flux Financiers § Gestion des flux financiers « temps réels » § Reuters, GL, Bloomberg, Instinet § Gestion du parc des stations transactionnelles § Délocalisées § Adhérent
Dérivés & Structurés Actions Informatique Front-Office § Informatique Front-Office / Flux Financiers § Gestion des flux financiers « temps réels » § Reuters, GL, Bloomberg, Instinet § Gestion du parc des stations transactionnelles § Délocalisées § Adhérent
 Dérivés & Structurés Actions Informatique Front-Office § Informatique Front-Office / Développement § Développement DLL en C++ § Modèles quantitatifs R&D
Dérivés & Structurés Actions Informatique Front-Office § Informatique Front-Office / Développement § Développement DLL en C++ § Modèles quantitatifs R&D
 Dérivés & Structurés Actions Département Juridique § Département Juristes de marchés § Programmes d’émission (prospectus, memorandum) § Contrats d’émission § Confirmations d’opérations § Validation montages
Dérivés & Structurés Actions Département Juridique § Département Juristes de marchés § Programmes d’émission (prospectus, memorandum) § Contrats d’émission § Confirmations d’opérations § Validation montages
 Dérivés & Structurés Actions Département Juridique § Département Fiscalistes § Traitement fiscal des opérations § Personnes morales § Personnes physiques
Dérivés & Structurés Actions Département Juridique § Département Fiscalistes § Traitement fiscal des opérations § Personnes morales § Personnes physiques
 Dérivés & Structurés Actions R&D § Département R&D Quantitative § «Quants» § Modèles stochastiques HJM sur les Taux BGM sur les Taux CRR sur les Actions Merton sur le Crédit § Procédures numériques Monte Carlo sur les Actions
Dérivés & Structurés Actions R&D § Département R&D Quantitative § «Quants» § Modèles stochastiques HJM sur les Taux BGM sur les Taux CRR sur les Actions Merton sur le Crédit § Procédures numériques Monte Carlo sur les Actions
 Dérivés & Structurés Actions R&D § Département R&D Economique § Economistes § Stratégistes § Recherche Actions (analyse)
Dérivés & Structurés Actions R&D § Département R&D Economique § Economistes § Stratégistes § Recherche Actions (analyse)
 Dérivés & Structurés Actions Vendeurs Sales § Vendeurs Cash § Placements Primaires (IPO) § Prise ferme § Book Building § Placements Secondaires § Market Making § Brokerage § Négociation de Blocs « Bought Deal »
Dérivés & Structurés Actions Vendeurs Sales § Vendeurs Cash § Placements Primaires (IPO) § Prise ferme § Book Building § Placements Secondaires § Market Making § Brokerage § Négociation de Blocs « Bought Deal »
 Dérivés & Structurés Actions Vendeurs Sales § Vendeurs Dérivés § Dérivés sur marchés organisés § Futures § Options vanilles § Dérivés sur marchés de gré à gré (OTC) § Forward § Options vanilles § Options exotiques § Produits Structurés § Négociation de Blocs « Bought Deal »
Dérivés & Structurés Actions Vendeurs Sales § Vendeurs Dérivés § Dérivés sur marchés organisés § Futures § Options vanilles § Dérivés sur marchés de gré à gré (OTC) § Forward § Options vanilles § Options exotiques § Produits Structurés § Négociation de Blocs « Bought Deal »
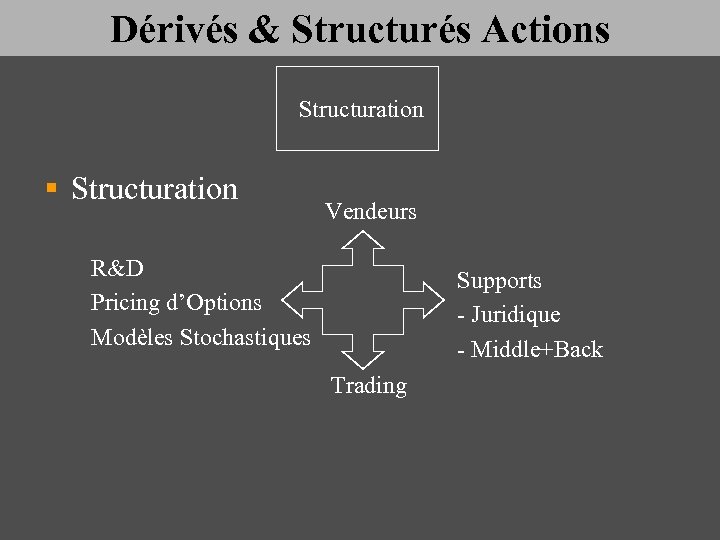 Dérivés & Structurés Actions Structuration § Structuration Vendeurs R&D Pricing d’Options Modèles Stochastiques Supports - Juridique - Middle+Back Trading
Dérivés & Structurés Actions Structuration § Structuration Vendeurs R&D Pricing d’Options Modèles Stochastiques Supports - Juridique - Middle+Back Trading
 Dérivés & Structurés Actions Structuration § Structuration § § § § Connaissance du contexte de marché Analyse de la problématique du client Synthèse de la solution financière la plus adaptée Montage financier le plus adapté Pricing Présentation au client «Topage» du deal § Suivi dans le marché secondaire du deal
Dérivés & Structurés Actions Structuration § Structuration § § § § Connaissance du contexte de marché Analyse de la problématique du client Synthèse de la solution financière la plus adaptée Montage financier le plus adapté Pricing Présentation au client «Topage» du deal § Suivi dans le marché secondaire du deal
 Dérivés & Structurés Actions Trading § Trading directionnel § § Positions « long » ou « short » Actions Dérivés (futures, options) Contrainte du « mark to market » ou MTM
Dérivés & Structurés Actions Trading § Trading directionnel § § Positions « long » ou « short » Actions Dérivés (futures, options) Contrainte du « mark to market » ou MTM
 Dérivés & Structurés Actions Trading § Trading Produits Structurés § Réplication du pay-off § Delta neutre § Véga neutre § Gamma neutre § Théta positif ou négatif § Temps continu ou discret § Optimisation du P&L § Aucune position directionnelle
Dérivés & Structurés Actions Trading § Trading Produits Structurés § Réplication du pay-off § Delta neutre § Véga neutre § Gamma neutre § Théta positif ou négatif § Temps continu ou discret § Optimisation du P&L § Aucune position directionnelle
 Dérivés & Structurés Actions Trading § Trading Arbitrages § Position directionnelle résiduelle § Position directionnelle sur des dérivés mathématiques d’ordre 2 § Position directionnelle sur spreads § Position directionnelle sur la volatilité
Dérivés & Structurés Actions Trading § Trading Arbitrages § Position directionnelle résiduelle § Position directionnelle sur des dérivés mathématiques d’ordre 2 § Position directionnelle sur spreads § Position directionnelle sur la volatilité
 Dérivés & Structurés Actions Senior Bankers § Senior Bankers § Interface Clients Grands Comptes / Spécialistes § Connaissance financière sur de multiples instruments § Marchés de Capitaux : Taux, Actions, Change, Commodities § Ingénierie Financière § Corporate Finance : M&A, OPE § Deal Makers
Dérivés & Structurés Actions Senior Bankers § Senior Bankers § Interface Clients Grands Comptes / Spécialistes § Connaissance financière sur de multiples instruments § Marchés de Capitaux : Taux, Actions, Change, Commodities § Ingénierie Financière § Corporate Finance : M&A, OPE § Deal Makers
 Dérivés & Structurés Actions Prêt Emprunt § Prêt / Emprunt § Connaissance des acteurs § Asset Management § Investisseurs Institutionnels § Connaissance des flux § Qui détient ? § Qui emprunte ?
Dérivés & Structurés Actions Prêt Emprunt § Prêt / Emprunt § Connaissance des acteurs § Asset Management § Investisseurs Institutionnels § Connaissance des flux § Qui détient ? § Qui emprunte ?
 Produits Structurés Actions 3ème Partie : description des produits structurés
Produits Structurés Actions 3ème Partie : description des produits structurés
 Supports juridiques q Titre de Créance Négociable TCN = CDN, BMTN q European Medium Term Note = EMTN (Euro-Bonds) q Obligations indexés q Option OTC q Warrants q Certificats
Supports juridiques q Titre de Créance Négociable TCN = CDN, BMTN q European Medium Term Note = EMTN (Euro-Bonds) q Obligations indexés q Option OTC q Warrants q Certificats
 Classification des Produits Structurés Actions q «Event Driven» Opportunités q Thématiques – Sectoriels q Produits de Volatilité q Produits réglementaires q Produits de couverture
Classification des Produits Structurés Actions q «Event Driven» Opportunités q Thématiques – Sectoriels q Produits de Volatilité q Produits réglementaires q Produits de couverture
 Produits : Capital Garanti § Principe général d’un Produit Structuré § Proposer aux Investisseurs § une fraction de la performance d’un actif financier « risqué » § une Action, un indice Actions, un Fonds § une garantie totale ou partielle du Capital à une échéance donnée § Capital Garanti § Capital protégé § Variantes § § garantir une fraction du capital seulement garantir le capital à tout moment cap sur la performance option sur moyenne
Produits : Capital Garanti § Principe général d’un Produit Structuré § Proposer aux Investisseurs § une fraction de la performance d’un actif financier « risqué » § une Action, un indice Actions, un Fonds § une garantie totale ou partielle du Capital à une échéance donnée § Capital Garanti § Capital protégé § Variantes § § garantir une fraction du capital seulement garantir le capital à tout moment cap sur la performance option sur moyenne
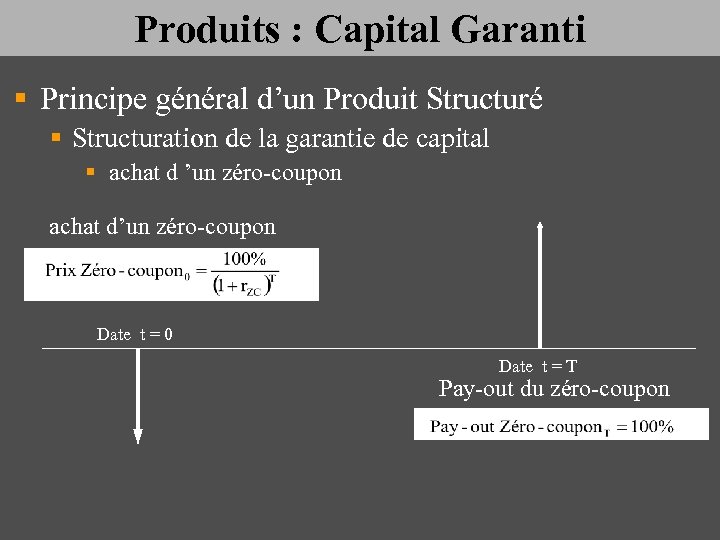 Produits : Capital Garanti § Principe général d’un Produit Structuré § Structuration de la garantie de capital § achat d ’un zéro-coupon achat d’un zéro-coupon Date t = 0 Date t = T Pay-out du zéro-coupon
Produits : Capital Garanti § Principe général d’un Produit Structuré § Structuration de la garantie de capital § achat d ’un zéro-coupon achat d’un zéro-coupon Date t = 0 Date t = T Pay-out du zéro-coupon
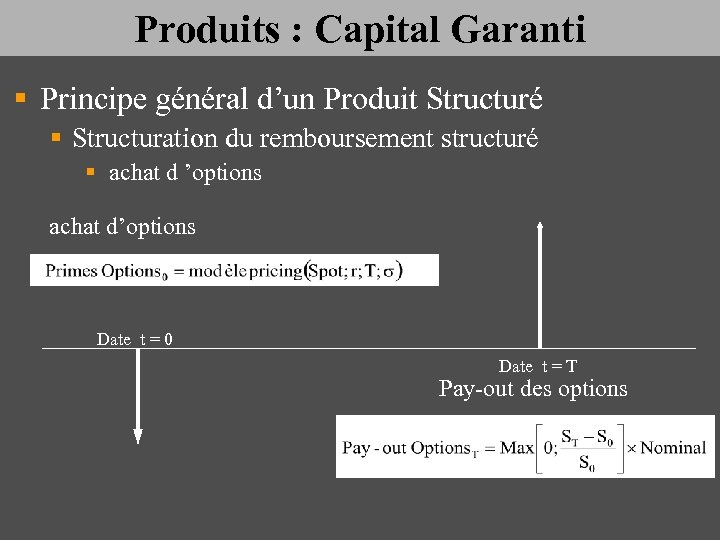 Produits : Capital Garanti § Principe général d’un Produit Structuré § Structuration du remboursement structuré § achat d ’options achat d’options Date t = 0 Date t = T Pay-out des options
Produits : Capital Garanti § Principe général d’un Produit Structuré § Structuration du remboursement structuré § achat d ’options achat d’options Date t = 0 Date t = T Pay-out des options
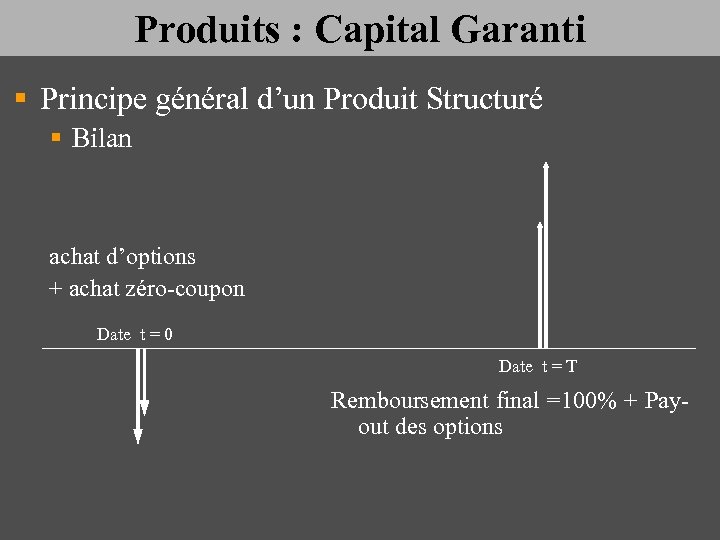 Produits : Capital Garanti § Principe général d’un Produit Structuré § Bilan achat d’options + achat zéro-coupon Date t = 0 Date t = T Remboursement final =100% + Payout des options
Produits : Capital Garanti § Principe général d’un Produit Structuré § Bilan achat d’options + achat zéro-coupon Date t = 0 Date t = T Remboursement final =100% + Payout des options
 Produits : Capital Garanti § Evolution du prix de la garantie au cours du temps
Produits : Capital Garanti § Evolution du prix de la garantie au cours du temps
 Produits : Capital Garanti § Structure de base § Investissement sur un actif sans risques + achat d’option sur actif risqué § La performance minimale garantie ne peut en aucun cas être supérieure ou égale au taux sans risque équivalent par Absence d’Opportunité d’Arbitrages § Sensibilités du produit structuré § § § sensibilité au taux sans risque sensibilité à la volatilité sensibilité au cap sensibilité à l’option sur moyenne sensibilité aux performances cumulées
Produits : Capital Garanti § Structure de base § Investissement sur un actif sans risques + achat d’option sur actif risqué § La performance minimale garantie ne peut en aucun cas être supérieure ou égale au taux sans risque équivalent par Absence d’Opportunité d’Arbitrages § Sensibilités du produit structuré § § § sensibilité au taux sans risque sensibilité à la volatilité sensibilité au cap sensibilité à l’option sur moyenne sensibilité aux performances cumulées
 Sensibilité Taux § Illustration de la sensibilité aux taux Plus les taux sont élevés plus la structure est favorable ! § Exemple : Durée 3 ans, 100% garantie, volatilité de 20% ð t = 7% on obtient 75% de la performance du CAC ð t = 5% on obtient 60% de la performance du CAC ð t = 3% on ne parvient plus qu’à environ 35%
Sensibilité Taux § Illustration de la sensibilité aux taux Plus les taux sont élevés plus la structure est favorable ! § Exemple : Durée 3 ans, 100% garantie, volatilité de 20% ð t = 7% on obtient 75% de la performance du CAC ð t = 5% on obtient 60% de la performance du CAC ð t = 3% on ne parvient plus qu’à environ 35%
 Sensibilité Taux § Sensibilité du produit structuré au taux d’intérêt
Sensibilité Taux § Sensibilité du produit structuré au taux d’intérêt
 Sensibilité Volatilité § Illustration de la sensibilité à la volatilité Plus la volatilité est élevée moins la structure est favorable ! § Exemple : Durée 3 ans, 100% garantie, taux de 5% ð s = 15% on obtient 70% de la performance du CAC ð s = 20% on obtient 60% de la performance du CAC ð s = 25% on obtient encore 50% de la performance du CAC
Sensibilité Volatilité § Illustration de la sensibilité à la volatilité Plus la volatilité est élevée moins la structure est favorable ! § Exemple : Durée 3 ans, 100% garantie, taux de 5% ð s = 15% on obtient 70% de la performance du CAC ð s = 20% on obtient 60% de la performance du CAC ð s = 25% on obtient encore 50% de la performance du CAC
 Sensibilité Cap § Illustration de l’effet Cap Le Cap consiste à limiter la performance au-delà d’un seuil § La limitation peut être totale ou partielle § totale : pas de participation au-delà du seuil § partielle : participation réduite au-delà du seuil § Exemple : Durée 3 ans, 100% garantie, taux de 3%, volatilité de 25% Seuil du Cap = 150% ð Indexation = 46% Seuil du Cap = 125% ð Indexation = 70% Pour mémoire sans plafonnement on avait 30%
Sensibilité Cap § Illustration de l’effet Cap Le Cap consiste à limiter la performance au-delà d’un seuil § La limitation peut être totale ou partielle § totale : pas de participation au-delà du seuil § partielle : participation réduite au-delà du seuil § Exemple : Durée 3 ans, 100% garantie, taux de 3%, volatilité de 25% Seuil du Cap = 150% ð Indexation = 46% Seuil du Cap = 125% ð Indexation = 70% Pour mémoire sans plafonnement on avait 30%
 Sensibilité à l’option moyenne § Illustration de l’effet option moyenne On calcule la performance sur une moyenne des cours tout au long de la période § Conséquence : - réduction de l’espérance de gains donc réduction de la prime d’option - augmentation de l’indexation § Exemple : Durée 3 ans, 100% garantie, taux de 3%, volatilité de 25% L’indexation est de 50% pour une option moyenne mensuelle Pour mémoire sans moyenne on avait 30%
Sensibilité à l’option moyenne § Illustration de l’effet option moyenne On calcule la performance sur une moyenne des cours tout au long de la période § Conséquence : - réduction de l’espérance de gains donc réduction de la prime d’option - augmentation de l’indexation § Exemple : Durée 3 ans, 100% garantie, taux de 3%, volatilité de 25% L’indexation est de 50% pour une option moyenne mensuelle Pour mémoire sans moyenne on avait 30%
 Produits : Capital Garanti § Principe § Proposer à un investisseur une partie de la performance d’un indice (ou d’une action), tout en garantissant le capital à une certaine échéance § Variantes § § § garantir une fraction du capital seulement garantir le capital uniquement à la maturité plafonnement de la participation performance moyenne performance cumulées
Produits : Capital Garanti § Principe § Proposer à un investisseur une partie de la performance d’un indice (ou d’une action), tout en garantissant le capital à une certaine échéance § Variantes § § § garantir une fraction du capital seulement garantir le capital uniquement à la maturité plafonnement de la participation performance moyenne performance cumulées
 Produits : Capital Garanti • Structure de base § Placement sans risques et achat d’option § En pratique, on peut répliquer l’option avec une stratégie dynamique afin de faciliter la valorisation continue • Sensibilité § § § au taux sans risque à la volatilité au plafonnement moyenne performances cumulées
Produits : Capital Garanti • Structure de base § Placement sans risques et achat d’option § En pratique, on peut répliquer l’option avec une stratégie dynamique afin de faciliter la valorisation continue • Sensibilité § § § au taux sans risque à la volatilité au plafonnement moyenne performances cumulées
 Capital Garanti : Effet Taux § Plus les taux sont élevés plus la structure est favorable ! § Exemple : § Durée 3 ans, 100% garantie, volatilité de 20% §ð t = 7% on obtient 75% de la performance du CAC §ð t = 5% on obtient 60% de la performance du CAC §ð t = 3% on ne parvient plus qu’à environ 35%
Capital Garanti : Effet Taux § Plus les taux sont élevés plus la structure est favorable ! § Exemple : § Durée 3 ans, 100% garantie, volatilité de 20% §ð t = 7% on obtient 75% de la performance du CAC §ð t = 5% on obtient 60% de la performance du CAC §ð t = 3% on ne parvient plus qu’à environ 35%
 Capital Garanti : Effet Volatilité § Plus la volatilité est élevée moins la structure est favorable ! § Exemple : § Durée 3 ans, 100% garantie, taux de 5% §ð s = 15% on obtient 70% de la performance du CAC §ð s = 20% on obtient 60% de la performance du CAC §ð s = 25% on obtient encore 50% de la performance du CAC
Capital Garanti : Effet Volatilité § Plus la volatilité est élevée moins la structure est favorable ! § Exemple : § Durée 3 ans, 100% garantie, taux de 5% §ð s = 15% on obtient 70% de la performance du CAC §ð s = 20% on obtient 60% de la performance du CAC §ð s = 25% on obtient encore 50% de la performance du CAC
 Capital Garanti : Plafonnement § Le plafonnement consiste à limiter la performance au-delà d’un seuil § La limitation peut être totale ou partielle § totale : pas de participation au-delà du seuil § partielle : participation réduite au-delà du seuil § Exemple : plafonnement total § Durée 3 ans, 100% garantie, taux de 3%, volatilité de 25% § Seuil = 150% ð Participation = 46% § Seuil = 125% ð Participation = 70% § Pour mémoire sans plafonnement on avait 30%
Capital Garanti : Plafonnement § Le plafonnement consiste à limiter la performance au-delà d’un seuil § La limitation peut être totale ou partielle § totale : pas de participation au-delà du seuil § partielle : participation réduite au-delà du seuil § Exemple : plafonnement total § Durée 3 ans, 100% garantie, taux de 3%, volatilité de 25% § Seuil = 150% ð Participation = 46% § Seuil = 125% ð Participation = 70% § Pour mémoire sans plafonnement on avait 30%
 Capital Garanti : Moyenne § On calcul la performance sur une moyenne des cours tout au long de la période. § Ceci a pour conséquences de réduire les espérances de gains mais d’augmenter le pourcentage d’intéressement § Exemple : Moyenne Mensuelle § Durée 3 ans, 100% garantie, taux de 3%, volatilité de 25% § La participation est de 50% § Pour mémoire sans moyenne on avait 30%
Capital Garanti : Moyenne § On calcul la performance sur une moyenne des cours tout au long de la période. § Ceci a pour conséquences de réduire les espérances de gains mais d’augmenter le pourcentage d’intéressement § Exemple : Moyenne Mensuelle § Durée 3 ans, 100% garantie, taux de 3%, volatilité de 25% § La participation est de 50% § Pour mémoire sans moyenne on avait 30%
 Produits Structurés Actions 4ème partie : Trading
Produits Structurés Actions 4ème partie : Trading
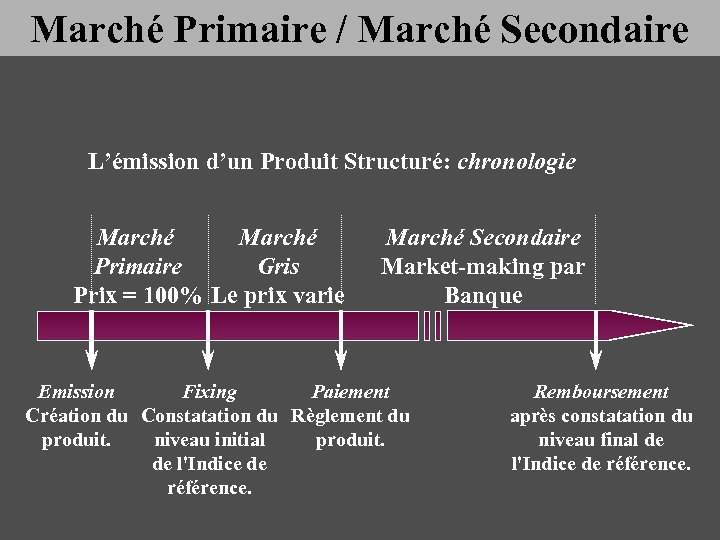 Marché Primaire / Marché Secondaire L’émission d’un Produit Structuré: chronologie Marché Primaire Gris Prix = 100% Le prix varie Marché Secondaire Market-making par Banque Emission Fixing Paiement Création du Constatation du Règlement du produit. niveau initial produit. de l'Indice de référence. Remboursement après constatation du niveau final de l'Indice de référence.
Marché Primaire / Marché Secondaire L’émission d’un Produit Structuré: chronologie Marché Primaire Gris Prix = 100% Le prix varie Marché Secondaire Market-making par Banque Emission Fixing Paiement Création du Constatation du Règlement du produit. niveau initial produit. de l'Indice de référence. Remboursement après constatation du niveau final de l'Indice de référence.
 Les coûts de transactions § Provenance des coûts de transactions: § Bid-ask § Market-Maker § Courtiers : coûts d’intermédiation § Modélisation: on peut considérer les coûts comme un polynôme de la valeur de l’action. § Coût = N*(k 0 +S*k 1) § En France on a k 1 compris entre 0. 001 et 0. 004 et k 0 = 0 § Aux US, k 0 est compris entre 0. 03 et 0. 06 et k 1 = 0
Les coûts de transactions § Provenance des coûts de transactions: § Bid-ask § Market-Maker § Courtiers : coûts d’intermédiation § Modélisation: on peut considérer les coûts comme un polynôme de la valeur de l’action. § Coût = N*(k 0 +S*k 1) § En France on a k 1 compris entre 0. 001 et 0. 004 et k 0 = 0 § Aux US, k 0 est compris entre 0. 03 et 0. 06 et k 1 = 0
 Rappel sur la Stratégie de B&S § Le cours de l’actif suit une loi log-normale § Pour couvrir parfaitement une option, il suffit, d’après le modèle de Black et Scholes : - d’acheter (ou de vendre) des actions - de placer (ou d’emprunter) le cash correspondant au taux sans risque. - La réplication est parfaite si : § Le réajustement est continu § Les taux et la volatilité sont constants § Il n’y a aucun coût de transaction
Rappel sur la Stratégie de B&S § Le cours de l’actif suit une loi log-normale § Pour couvrir parfaitement une option, il suffit, d’après le modèle de Black et Scholes : - d’acheter (ou de vendre) des actions - de placer (ou d’emprunter) le cash correspondant au taux sans risque. - La réplication est parfaite si : § Le réajustement est continu § Les taux et la volatilité sont constants § Il n’y a aucun coût de transaction
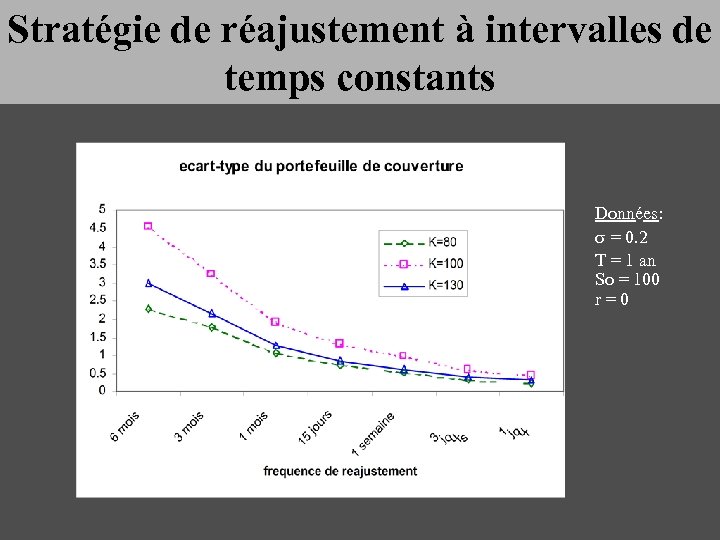 Stratégie de réajustement à intervalles de temps constants Données: s = 0. 2 T = 1 an So = 100 r = 0
Stratégie de réajustement à intervalles de temps constants Données: s = 0. 2 T = 1 an So = 100 r = 0
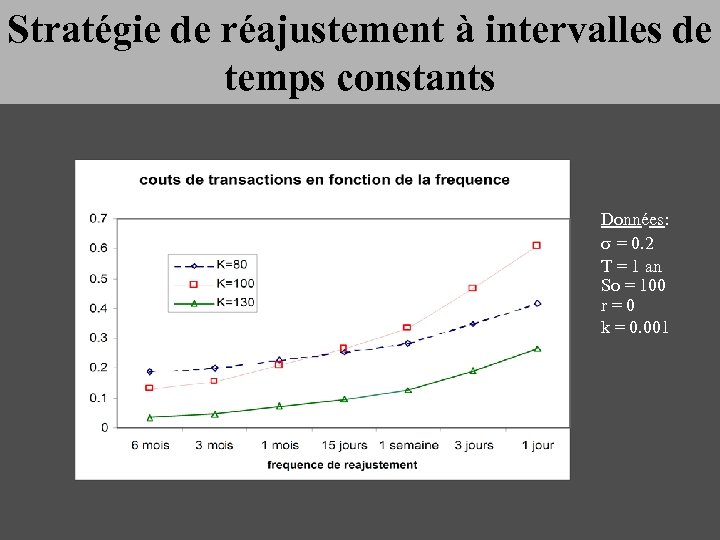 Stratégie de réajustement à intervalles de temps constants Données: s = 0. 2 T = 1 an So = 100 r = 0 k = 0. 001
Stratégie de réajustement à intervalles de temps constants Données: s = 0. 2 T = 1 an So = 100 r = 0 k = 0. 001
 Stratégie optimale : Call § So = K = 100, s = 20%, T=1 et r = d = 0 Prime = 7. 96$, Notionnel = 1 million de titres § Prime payée = 7, 960, 000 $
Stratégie optimale : Call § So = K = 100, s = 20%, T=1 et r = d = 0 Prime = 7. 96$, Notionnel = 1 million de titres § Prime payée = 7, 960, 000 $
 Produits Capital Garanti 5ème partie : Eléments de pricing
Produits Capital Garanti 5ème partie : Eléments de pricing
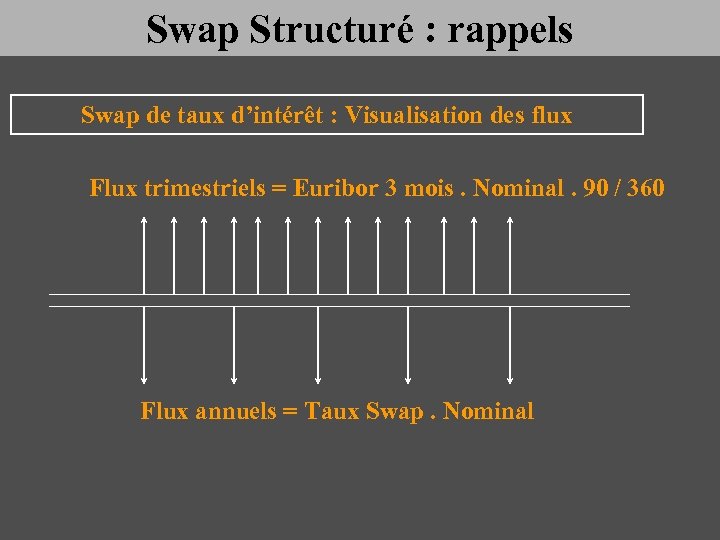 Swap Structuré : rappels Swap de taux d’intérêt : Visualisation des flux Flux trimestriels = Euribor 3 mois. Nominal. 90 / 360 Flux annuels = Taux Swap. Nominal
Swap Structuré : rappels Swap de taux d’intérêt : Visualisation des flux Flux trimestriels = Euribor 3 mois. Nominal. 90 / 360 Flux annuels = Taux Swap. Nominal
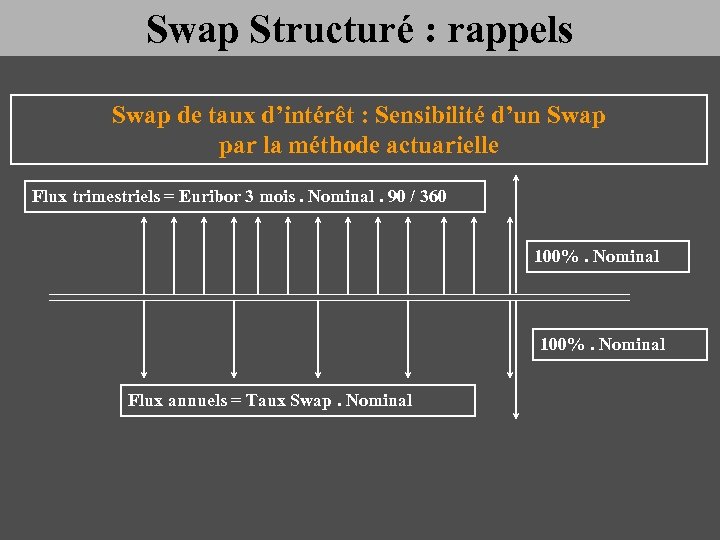 Swap Structuré : rappels Swap de taux d’intérêt : Sensibilité d’un Swap par la méthode actuarielle Flux trimestriels = Euribor 3 mois. Nominal. 90 / 360 100%. Nominal Flux annuels = Taux Swap. Nominal
Swap Structuré : rappels Swap de taux d’intérêt : Sensibilité d’un Swap par la méthode actuarielle Flux trimestriels = Euribor 3 mois. Nominal. 90 / 360 100%. Nominal Flux annuels = Taux Swap. Nominal
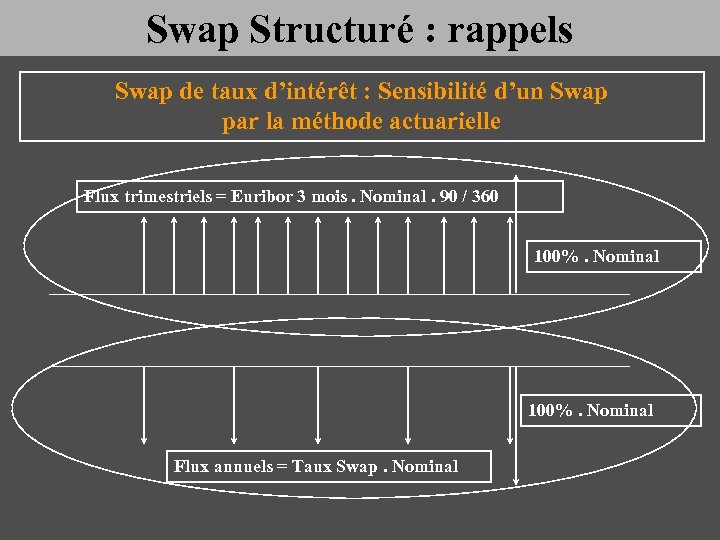 Swap Structuré : rappels Swap de taux d’intérêt : Sensibilité d’un Swap par la méthode actuarielle Flux trimestriels = Euribor 3 mois. Nominal. 90 / 360 100%. Nominal Flux annuels = Taux Swap. Nominal
Swap Structuré : rappels Swap de taux d’intérêt : Sensibilité d’un Swap par la méthode actuarielle Flux trimestriels = Euribor 3 mois. Nominal. 90 / 360 100%. Nominal Flux annuels = Taux Swap. Nominal
 Swap Structuré : rappels Swap de taux d ’intérêt : Sensibilité d’un Swap par la méthode actuarielle Swap = + Obligation classique à taux fixe remboursée à 100% in fine - Obligation classique à taux variable remboursée à 100% in fine donc logiquement : Sensibilité Swap = Sensibilité oblig à taux fixe - Sensibilité oblig à taux variable
Swap Structuré : rappels Swap de taux d ’intérêt : Sensibilité d’un Swap par la méthode actuarielle Swap = + Obligation classique à taux fixe remboursée à 100% in fine - Obligation classique à taux variable remboursée à 100% in fine donc logiquement : Sensibilité Swap = Sensibilité oblig à taux fixe - Sensibilité oblig à taux variable
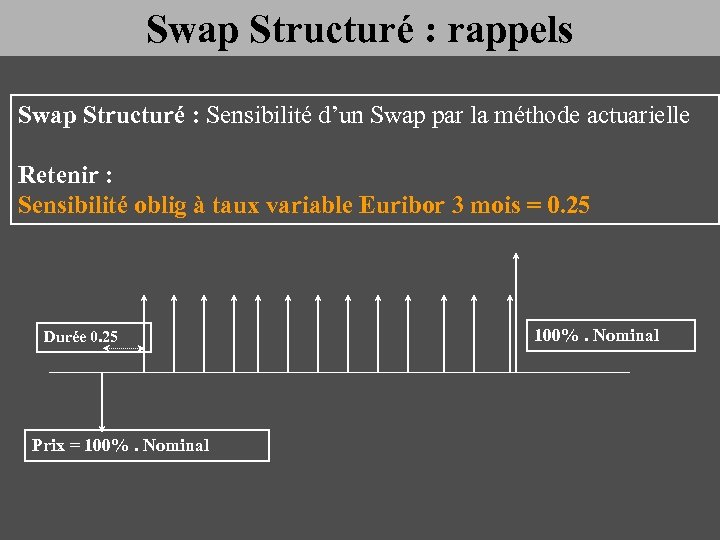 Swap Structuré : rappels Swap Structuré : Sensibilité d’un Swap par la méthode actuarielle Retenir : Sensibilité oblig à taux variable Euribor 3 mois = 0. 25 Durée 0. 25 Prix = 100%. Nominal
Swap Structuré : rappels Swap Structuré : Sensibilité d’un Swap par la méthode actuarielle Retenir : Sensibilité oblig à taux variable Euribor 3 mois = 0. 25 Durée 0. 25 Prix = 100%. Nominal
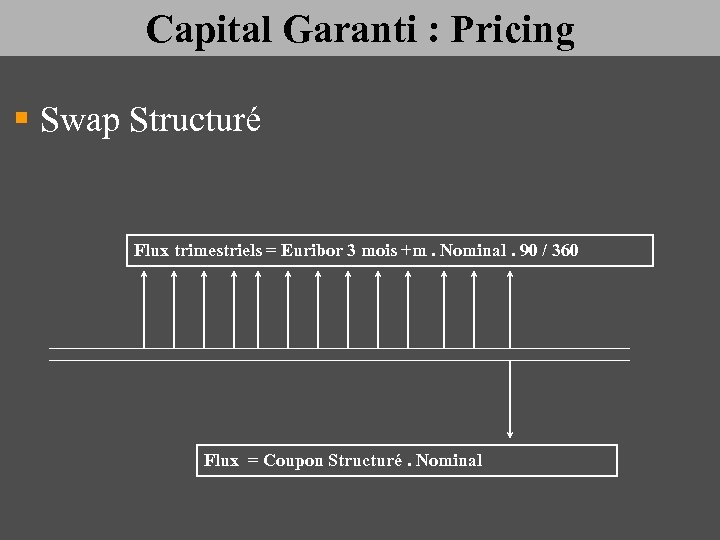 Capital Garanti : Pricing § Swap Structuré Flux trimestriels = Euribor 3 mois +m. Nominal. 90 / 360 Flux = Coupon Structuré. Nominal
Capital Garanti : Pricing § Swap Structuré Flux trimestriels = Euribor 3 mois +m. Nominal. 90 / 360 Flux = Coupon Structuré. Nominal
 Capital Garanti : Pricing § Swap Structuré : cas classique Hypothèses sur le Produit Structuré BMTN : - Capital garanti 100% - Prix émission 100% - Remboursement = 100% + Coupon Structuré
Capital Garanti : Pricing § Swap Structuré : cas classique Hypothèses sur le Produit Structuré BMTN : - Capital garanti 100% - Prix émission 100% - Remboursement = 100% + Coupon Structuré
 Capital Garanti : Pricing § Swap Structuré : jambe Euribor NPV (jambe Euribor+m)= 100% + NPV(m)-100%. Z(0, T) Notations : DF = Discount Factor Z(0, T) = Prix du zéro-coupon de maturité T NPV(jambe Euribor+ m) = 100% + m. DF -100%. Z(0, T)
Capital Garanti : Pricing § Swap Structuré : jambe Euribor NPV (jambe Euribor+m)= 100% + NPV(m)-100%. Z(0, T) Notations : DF = Discount Factor Z(0, T) = Prix du zéro-coupon de maturité T NPV(jambe Euribor+ m) = 100% + m. DF -100%. Z(0, T)
 Capital Garanti : Pricing § Swap Structuré : jambe Euribor Définition du Discount Factor :
Capital Garanti : Pricing § Swap Structuré : jambe Euribor Définition du Discount Factor :
 Capital Garanti : Pricing § Swap Structuré: jambe structurée NPV (Coupon Structuré) = Coupon Structuré. Z(0, T) Notons Z(0, T) = Prix du zéro-coupon de maturité T
Capital Garanti : Pricing § Swap Structuré: jambe structurée NPV (Coupon Structuré) = Coupon Structuré. Z(0, T) Notons Z(0, T) = Prix du zéro-coupon de maturité T
 Capital Garanti : Pricing § Swap Structuré: Calcul du coupon structuré NPV (Coupon Structuré) = NPV(Jambe Euribor+m) - Commissions
Capital Garanti : Pricing § Swap Structuré: Calcul du coupon structuré NPV (Coupon Structuré) = NPV(Jambe Euribor+m) - Commissions
 Capital Garanti : Pricing § Swap Structuré : Calcul du coupon structuré NPV (Coupon Structuré) = NPV(Jambe Euribor+m) - Commissions
Capital Garanti : Pricing § Swap Structuré : Calcul du coupon structuré NPV (Coupon Structuré) = NPV(Jambe Euribor+m) - Commissions
 Capital Garanti : Pricing § Pricing du BMTN
Capital Garanti : Pricing § Pricing du BMTN
 Capital Garanti : Pricing § Pricing du Swap Structuré
Capital Garanti : Pricing § Pricing du Swap Structuré
 Capital Garanti : Pricing § Pricing du Swap Structuré Hypothèse : m = spread
Capital Garanti : Pricing § Pricing du Swap Structuré Hypothèse : m = spread
 Capital Garanti : Pricing § Swap Structuré dans le cas général Hypothèses sur le Produit Structuré BMTN : • Capital garanti G% (<> 100%) • Prix émission Pe% (<> 100%) • Remboursement = G% + Coupon Structuré
Capital Garanti : Pricing § Swap Structuré dans le cas général Hypothèses sur le Produit Structuré BMTN : • Capital garanti G% (<> 100%) • Prix émission Pe% (<> 100%) • Remboursement = G% + Coupon Structuré
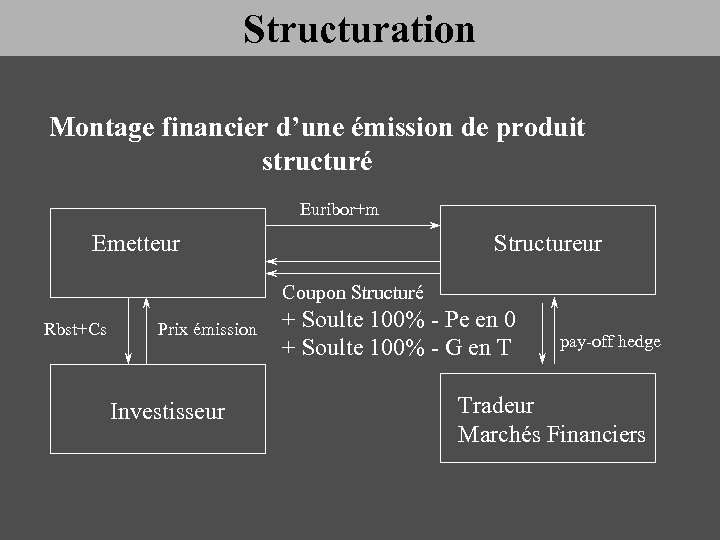 Structuration Montage financier d’une émission de produit structuré Euribor+m Emetteur Structureur Coupon Structuré Rbst+Cs Prix émission Investisseur + Soulte 100% - Pe en 0 + Soulte 100% - G en T pay-off hedge Tradeur Marchés Financiers
Structuration Montage financier d’une émission de produit structuré Euribor+m Emetteur Structureur Coupon Structuré Rbst+Cs Prix émission Investisseur + Soulte 100% - Pe en 0 + Soulte 100% - G en T pay-off hedge Tradeur Marchés Financiers
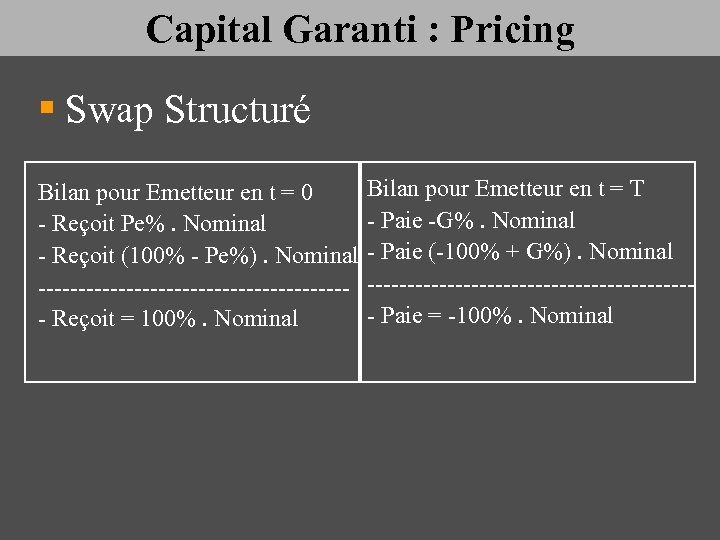 Capital Garanti : Pricing § Swap Structuré Bilan pour Emetteur en t = 0 - Reçoit Pe%. Nominal - Reçoit (100% - Pe%). Nominal -------------------- Reçoit = 100%. Nominal Bilan pour Emetteur en t = T - Paie -G%. Nominal - Paie (-100% + G%). Nominal --------------------- Paie = -100%. Nominal
Capital Garanti : Pricing § Swap Structuré Bilan pour Emetteur en t = 0 - Reçoit Pe%. Nominal - Reçoit (100% - Pe%). Nominal -------------------- Reçoit = 100%. Nominal Bilan pour Emetteur en t = T - Paie -G%. Nominal - Paie (-100% + G%). Nominal --------------------- Paie = -100%. Nominal
 Reverse Convertible Principe : C’est un produit destiné aux investisseurs ou au réseau et jusqu'à aujourd’hui principalement émis par les banques. L’Investisseur est vendeur d’un put et en échange vous recevez la prime étalée sur plusieurs années. Le put vendu peut être de tout type et sur tout sous-jacent. Le risque de crédit est sur l'émetteur obligataire et est limité au principal.
Reverse Convertible Principe : C’est un produit destiné aux investisseurs ou au réseau et jusqu'à aujourd’hui principalement émis par les banques. L’Investisseur est vendeur d’un put et en échange vous recevez la prime étalée sur plusieurs années. Le put vendu peut être de tout type et sur tout sous-jacent. Le risque de crédit est sur l'émetteur obligataire et est limité au principal.
 Étude de cas n° 1 BMTN indexé CAC 40
Étude de cas n° 1 BMTN indexé CAC 40
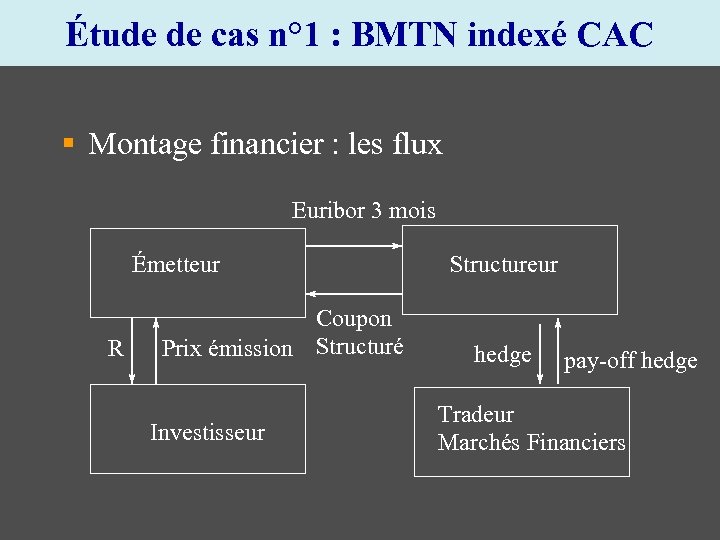 Étude de cas n° 1 : BMTN indexé CAC § Montage financier : les flux Euribor 3 mois Émetteur R Coupon Prix émission Structuré Investisseur Structureur hedge pay-off hedge Tradeur Marchés Financiers
Étude de cas n° 1 : BMTN indexé CAC § Montage financier : les flux Euribor 3 mois Émetteur R Coupon Prix émission Structuré Investisseur Structureur hedge pay-off hedge Tradeur Marchés Financiers
 Étude de cas n° 1 : BMTN indexé CAC § Montage financier : le produit § un BMTN Structuré de nominal N § une formule de remboursement faisant intervenir un calcul sur la performance de l’indice CAC : R/N = 105% + Indexation% x Min[40% ; Max[0; Coursfinal/Coursinitial-1]] R/N = 105% + Coupon Structuré% = I% x Min[40% ; Max[0; Coursfinal/Coursinitial-1]]
Étude de cas n° 1 : BMTN indexé CAC § Montage financier : le produit § un BMTN Structuré de nominal N § une formule de remboursement faisant intervenir un calcul sur la performance de l’indice CAC : R/N = 105% + Indexation% x Min[40% ; Max[0; Coursfinal/Coursinitial-1]] R/N = 105% + Coupon Structuré% = I% x Min[40% ; Max[0; Coursfinal/Coursinitial-1]]
 Étude de cas n° 1 : BMTN indexé CAC § Montage financier : Bilan pour Emetteur § § § Emetteur Emetteur reçoit le Prix d’émission en t = 0 paie le remboursement 105%+C% en t = T reçoit C% en t = T dans le swap d’émission reçoit une soulte de 5% en t = T paie Euribor 3 mois dans le swap d’émission § Bilan Emetteur : § Emetteur reçoit le prix d’émission en t = 0 § Emetteur paie Euribor 3 mois
Étude de cas n° 1 : BMTN indexé CAC § Montage financier : Bilan pour Emetteur § § § Emetteur Emetteur reçoit le Prix d’émission en t = 0 paie le remboursement 105%+C% en t = T reçoit C% en t = T dans le swap d’émission reçoit une soulte de 5% en t = T paie Euribor 3 mois dans le swap d’émission § Bilan Emetteur : § Emetteur reçoit le prix d’émission en t = 0 § Emetteur paie Euribor 3 mois
 Étude de cas n° 1 : BMTN indexé CAC § Montage financier : Bilan pour l’Emetteur § Avant swap d’émission : § émission d’un produit financier structuré avec une formule de remboursement complexe R/N = 105% + Indexation% x Min[40% ; Max[0; Coursfinal/Coursinitial-1]] § Après swap d’émission : § emprunt classique Emprunt flotteur Euribor 3 mois remboursé au pair
Étude de cas n° 1 : BMTN indexé CAC § Montage financier : Bilan pour l’Emetteur § Avant swap d’émission : § émission d’un produit financier structuré avec une formule de remboursement complexe R/N = 105% + Indexation% x Min[40% ; Max[0; Coursfinal/Coursinitial-1]] § Après swap d’émission : § emprunt classique Emprunt flotteur Euribor 3 mois remboursé au pair
 Étude de cas n° 1 : BMTN indexé CAC § Montage financier : Bilan pour Investisseur § Emetteur paie le prix d’émission en t = 0 reçoit le remboursement 105%+C% en t = T § Montage financier : Bilan Structureur § Structureur reçoit Euribor 3 mois § Structureur paie Coupon Structuré C%
Étude de cas n° 1 : BMTN indexé CAC § Montage financier : Bilan pour Investisseur § Emetteur paie le prix d’émission en t = 0 reçoit le remboursement 105%+C% en t = T § Montage financier : Bilan Structureur § Structureur reçoit Euribor 3 mois § Structureur paie Coupon Structuré C%
 Étude de cas n° 1 : BMTN indexé CAC § Montage financier : le produit § un BMTN 1 an de nominal N § Remboursement R = 105% § Coupon in fine Structuré C/N = Indexation% x Min[40% ; Max[0; Coursfinal/Coursinitial-1]] § Coursfinal : cours clôture CAC à échéance en t = T § Coursinitial : cours clôture CAC lors de l’émission en t = 0
Étude de cas n° 1 : BMTN indexé CAC § Montage financier : le produit § un BMTN 1 an de nominal N § Remboursement R = 105% § Coupon in fine Structuré C/N = Indexation% x Min[40% ; Max[0; Coursfinal/Coursinitial-1]] § Coursfinal : cours clôture CAC à échéance en t = T § Coursinitial : cours clôture CAC lors de l’émission en t = 0
 Étude de cas n° 1 : BMTN indexé CAC § Montage financier : le coupon structuré § Coupon in fine Structuré C/N = Indexation% x Min[40% ; Max[0; Coursfinal/Coursinitial-1]] ou C= Index% x Min[40% ; Max[0; Coursfinal/Coursinitial-1]]x. N ou C= q x Min[40% ; Max[0; Coursfinal - Coursinitial]] avec q = Indexation% x N / Coursinitial
Étude de cas n° 1 : BMTN indexé CAC § Montage financier : le coupon structuré § Coupon in fine Structuré C/N = Indexation% x Min[40% ; Max[0; Coursfinal/Coursinitial-1]] ou C= Index% x Min[40% ; Max[0; Coursfinal/Coursinitial-1]]x. N ou C= q x Min[40% ; Max[0; Coursfinal - Coursinitial]] avec q = Indexation% x N / Coursinitial
 Étude de cas n° 1 : BMTN indexé CAC § Montage financier : le coupon structuré § Notion de quantité d’options C= quantité d’options q avec q = Indexation% x N / Coursinitial
Étude de cas n° 1 : BMTN indexé CAC § Montage financier : le coupon structuré § Notion de quantité d’options C= quantité d’options q avec q = Indexation% x N / Coursinitial
 Étude de cas n° 1 : BMTN indexé CAC § Montage financier : options sur CAC § Call sur CAC à la monnaie spot Si ATM Spot : Strike = Coursinitial Call = q. Max[0 ; Coursfinal - Coursinitial ] Call = Indexation%. Max[0 ; Coursfinal - Coursinitial ]. N § Call sur CAC en dehors de la monnaie de 40% Strike = K= Coursinitial x 140% Call = q. Max[0 ; Coursfinal - K ] Call = Indexation%. Max[0 ; Coursfinal-Coursinitial x 140%]. N
Étude de cas n° 1 : BMTN indexé CAC § Montage financier : options sur CAC § Call sur CAC à la monnaie spot Si ATM Spot : Strike = Coursinitial Call = q. Max[0 ; Coursfinal - Coursinitial ] Call = Indexation%. Max[0 ; Coursfinal - Coursinitial ]. N § Call sur CAC en dehors de la monnaie de 40% Strike = K= Coursinitial x 140% Call = q. Max[0 ; Coursfinal - K ] Call = Indexation%. Max[0 ; Coursfinal-Coursinitial x 140%]. N
 Étude de cas n° 1 : BMTN indexé CAC § Montage financier : options sur CAC § Achat de q Call sur CAC à la monnaie spot § vente de q Call sur CAC avec strike en dehors de la monnaie Achat Call = q. Max[0 ; Coursfinal - Coursinitial ] Vente Call = -q. Max[0; Coursfinal-Coursinitial x 140%] donc Call Spread = q. Min[Coursinitial x 140% - Coursinitial ; Max[0; Coursfinal - Coursinitial]
Étude de cas n° 1 : BMTN indexé CAC § Montage financier : options sur CAC § Achat de q Call sur CAC à la monnaie spot § vente de q Call sur CAC avec strike en dehors de la monnaie Achat Call = q. Max[0 ; Coursfinal - Coursinitial ] Vente Call = -q. Max[0; Coursfinal-Coursinitial x 140%] donc Call Spread = q. Min[Coursinitial x 140% - Coursinitial ; Max[0; Coursfinal - Coursinitial]
 Étude de cas n° 1 : BMTN indexé CAC § Montage financier : options sur CAC Call Spread = q x Min[Coursinitial x 140% - Coursinitial ; Max[0; Coursfinal - Coursinitial] Call Spread = I%. Min[40% ; Max[0; Coursfinal / Coursinitial - 1]]x. N Rappel du coupon structuré : Coupon structuré = I%. Min[40%; Max[0; Coursfinal/Coursinitial - 1]]x. N Coupon Structuré = Call spread 100% - 140% sur CAC pour un nominal égal à Indexation%. N
Étude de cas n° 1 : BMTN indexé CAC § Montage financier : options sur CAC Call Spread = q x Min[Coursinitial x 140% - Coursinitial ; Max[0; Coursfinal - Coursinitial] Call Spread = I%. Min[40% ; Max[0; Coursfinal / Coursinitial - 1]]x. N Rappel du coupon structuré : Coupon structuré = I%. Min[40%; Max[0; Coursfinal/Coursinitial - 1]]x. N Coupon Structuré = Call spread 100% - 140% sur CAC pour un nominal égal à Indexation%. N
 Étude de cas n° 1 : BMTN indexé CAC § Pricing Rappel : swap d’émission 1ère jambe : Coupon structuré = Call spread sur CAC 2ème jambe : Euribor 3 mois
Étude de cas n° 1 : BMTN indexé CAC § Pricing Rappel : swap d’émission 1ère jambe : Coupon structuré = Call spread sur CAC 2ème jambe : Euribor 3 mois
 Étude de cas n° 1 : BMTN indexé CAC § Pricing : structuration § Commission de placement : § Commission de montage : § Commission sur option : Comp Come Como NPV(2ème Jambe Euribor) - Comp - Como - Come = NVP(1ère jambe coupon structuré)
Étude de cas n° 1 : BMTN indexé CAC § Pricing : structuration § Commission de placement : § Commission de montage : § Commission sur option : Comp Come Como NPV(2ème Jambe Euribor) - Comp - Como - Come = NVP(1ère jambe coupon structuré)
 Étude de cas n° 1 : BMTN indexé CAC § Pricing : applications numériques § 2ème jambe : Euribor 3 mois VAN = NPV = 10. 68% x Nominal
Étude de cas n° 1 : BMTN indexé CAC § Pricing : applications numériques § 2ème jambe : Euribor 3 mois VAN = NPV = 10. 68% x Nominal
 Étude de cas n° 1 : BMTN indexé CAC § Pricing : applications numériques § Call à la monnaie spot :
Étude de cas n° 1 : BMTN indexé CAC § Pricing : applications numériques § Call à la monnaie spot :
 Étude de cas n° 1 : BMTN indexé CAC § Pricing : applications numériques § Call à la monnaie spot :
Étude de cas n° 1 : BMTN indexé CAC § Pricing : applications numériques § Call à la monnaie spot :
 Étude de cas n° 1 : BMTN indexé CAC § Pricing : applications numériques § Call en dehors de monnaie :
Étude de cas n° 1 : BMTN indexé CAC § Pricing : applications numériques § Call en dehors de monnaie :
 Étude de cas n° 1 : BMTN indexé CAC § Pricing : applications numériques § Call en dehors de monnaie :
Étude de cas n° 1 : BMTN indexé CAC § Pricing : applications numériques § Call en dehors de monnaie :
 Étude de cas n° 1 : BMTN indexé CAC § Pricing : applications numériques NPV(Euribor) - Comp - Como - Come = prime option indexé Comp+Como+Come = NPV(Euribor) - prime option indexée
Étude de cas n° 1 : BMTN indexé CAC § Pricing : applications numériques NPV(Euribor) - Comp - Como - Come = prime option indexé Comp+Como+Come = NPV(Euribor) - prime option indexée
 Étude de cas n° 1 : BMTN indexé CAC § Pricing : applications numériques § Call Spread 100% - 140 % prime option non indexée : 14% prime option indexée : Indexation% * 14% § NPV(jambe Euribor 3 mois) = 10. 68% § Commissions : 1. 20%
Étude de cas n° 1 : BMTN indexé CAC § Pricing : applications numériques § Call Spread 100% - 140 % prime option non indexée : 14% prime option indexée : Indexation% * 14% § NPV(jambe Euribor 3 mois) = 10. 68% § Commissions : 1. 20%
 Étude de cas n° 1 : BMTN indexé CAC § Montage financier : calcul de l’indexation NPV(Euribor) - Comp - Como - Come = prime option indexé NPV(Euribor) - Commissions = prime option x Indexation NPV(Euribo r) - Commissions Indexation = prime option
Étude de cas n° 1 : BMTN indexé CAC § Montage financier : calcul de l’indexation NPV(Euribor) - Comp - Como - Come = prime option indexé NPV(Euribor) - Commissions = prime option x Indexation NPV(Euribo r) - Commissions Indexation = prime option
 Étude de cas n° 1 : BMTN indexé CAC § Montage financier : calcul de l’indexation Indexation = 10. 68%-1. 20% 14% Indexation = 68%
Étude de cas n° 1 : BMTN indexé CAC § Montage financier : calcul de l’indexation Indexation = 10. 68%-1. 20% 14% Indexation = 68%
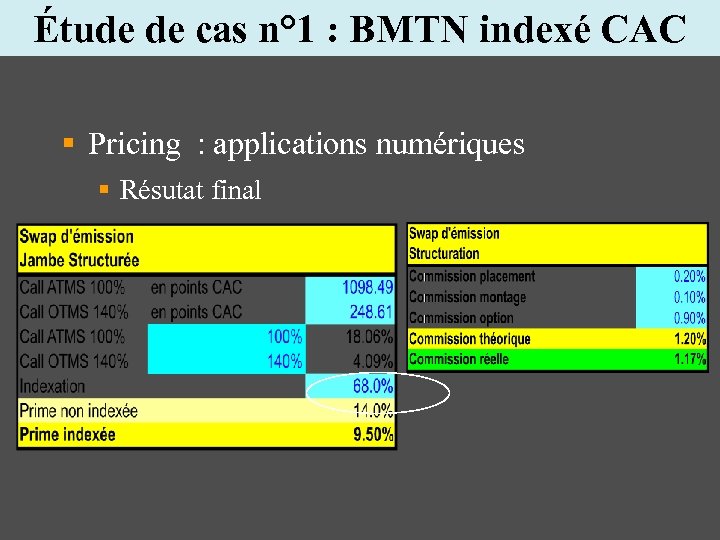 Étude de cas n° 1 : BMTN indexé CAC § Pricing : applications numériques § Résutat final
Étude de cas n° 1 : BMTN indexé CAC § Pricing : applications numériques § Résutat final
 Étude de cas n° 1 : BMTN indexé CAC § Pricing : hedge Opération n° 1 : Calcul du delta du Call Spread CAC Delta Call Spread = Delta Call 100% - Delta Call 140% Delta Call = Pr ime Call ( Spot + 1 ) - Pr ime Call ( Spot ) 1
Étude de cas n° 1 : BMTN indexé CAC § Pricing : hedge Opération n° 1 : Calcul du delta du Call Spread CAC Delta Call Spread = Delta Call 100% - Delta Call 140% Delta Call = Pr ime Call ( Spot + 1 ) - Pr ime Call ( Spot ) 1
 Étude de cas n° 1 : BMTN indexé CAC § Pricing : hedge Opération n° 1 : Calcul du delta du Call spread par option en Euro Call 100% Call 140%
Étude de cas n° 1 : BMTN indexé CAC § Pricing : hedge Opération n° 1 : Calcul du delta du Call spread par option en Euro Call 100% Call 140%
 Étude de cas n° 1 : BMTN indexé CAC § Pricing : hedge Opération n° 2 : Calcul du nominal d’Option Nominal d’Options = Indexation. Nominal BMTN Nominal d’Options = 68%. Nominal BMTN Nominal d’Options = 68%. 5 000 = 3 400 000 Euro
Étude de cas n° 1 : BMTN indexé CAC § Pricing : hedge Opération n° 2 : Calcul du nominal d’Option Nominal d’Options = Indexation. Nominal BMTN Nominal d’Options = 68%. Nominal BMTN Nominal d’Options = 68%. 5 000 = 3 400 000 Euro
 Étude de cas n° 1 : BMTN indexé CAC § Pricing : hedge Opération n° 3 : Calcul du nombre d’options Call Spread Nombre d’options q = Nominal d’Option CAC Spot Nombre d’options q = Indexation. Nominal BMTN CAC Spot Nombre d’options q = 559. 10
Étude de cas n° 1 : BMTN indexé CAC § Pricing : hedge Opération n° 3 : Calcul du nombre d’options Call Spread Nombre d’options q = Nominal d’Option CAC Spot Nombre d’options q = Indexation. Nominal BMTN CAC Spot Nombre d’options q = 559. 10
 Étude de cas n° 1 : BMTN indexé CAC § Pricing : hedge Opération n° 4 : Calcul du delta total du BMTN Delta total BMTN = q. Delta par Option Delta total BMTN = 559. 10. ( 0. 62 - 0. 235 ) = 215. 22 Euros
Étude de cas n° 1 : BMTN indexé CAC § Pricing : hedge Opération n° 4 : Calcul du delta total du BMTN Delta total BMTN = q. Delta par Option Delta total BMTN = 559. 10. ( 0. 62 - 0. 235 ) = 215. 22 Euros
 Étude de cas n° 1 : BMTN indexé CAC § Pricing : hedge Opération n° 5 : Calcul du nombre de contrats CAC 1 point de CAC = 10 Euros Delta total BMTN = 215. 22 Euros = 21. 5 contrats CAC
Étude de cas n° 1 : BMTN indexé CAC § Pricing : hedge Opération n° 5 : Calcul du nombre de contrats CAC 1 point de CAC = 10 Euros Delta total BMTN = 215. 22 Euros = 21. 5 contrats CAC
 Étude de cas n° 1 : BMTN indexé CAC § Pricing : Synthèse du hedge Call 100% Call 140% Nombre de contrats CAC = 21. 5
Étude de cas n° 1 : BMTN indexé CAC § Pricing : Synthèse du hedge Call 100% Call 140% Nombre de contrats CAC = 21. 5
 Étude de cas n° 1 : BMTN indexé CAC § Pricing : P&L du Tradeur : § vendeur du Call spread CAC 100%-140% § acheteur de 21. 55 contrats CAC Hypothèse : § hausse du CAC de +5% en 2 jours
Étude de cas n° 1 : BMTN indexé CAC § Pricing : P&L du Tradeur : § vendeur du Call spread CAC 100%-140% § acheteur de 21. 55 contrats CAC Hypothèse : § hausse du CAC de +5% en 2 jours
 Étude de cas n° 1 : BMTN indexé CAC § Pricing : P&L du Tradeur Variation prime Call 100% Variation prime Call 140% Variation prime Call 100% - 140% = -117. 27
Étude de cas n° 1 : BMTN indexé CAC § Pricing : P&L du Tradeur Variation prime Call 100% Variation prime Call 140% Variation prime Call 100% - 140% = -117. 27
 Étude de cas n° 1 : BMTN indexé CAC § Pricing : P&L du Tradeur Variation prime Call 100% - 140%
Étude de cas n° 1 : BMTN indexé CAC § Pricing : P&L du Tradeur Variation prime Call 100% - 140%
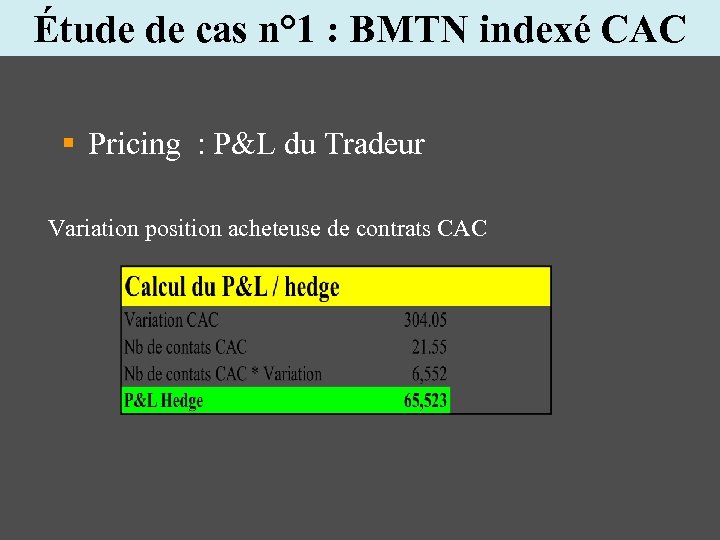 Étude de cas n° 1 : BMTN indexé CAC § Pricing : P&L du Tradeur Variation position acheteuse de contrats CAC
Étude de cas n° 1 : BMTN indexé CAC § Pricing : P&L du Tradeur Variation position acheteuse de contrats CAC
 Étude de cas n° 1 : BMTN indexé CAC § Pricing : P&L du Tradeur Variation position vendeuse de call spread 100%-140% Variation position acheteuse de contrats CAC
Étude de cas n° 1 : BMTN indexé CAC § Pricing : P&L du Tradeur Variation position vendeuse de call spread 100%-140% Variation position acheteuse de contrats CAC
 Étude de cas n° 1 : BMTN indexé CAC § Secondaire : valorisation du BMTN indexé Cac § Valorisation à t = 3 mois § Hypothèses : § Hausse du taux : +0. 50% § Volatilité 100% passe de 26% à 30% § Volatilité 140% passe de 22% à 28% § CAC progresse de +15%
Étude de cas n° 1 : BMTN indexé CAC § Secondaire : valorisation du BMTN indexé Cac § Valorisation à t = 3 mois § Hypothèses : § Hausse du taux : +0. 50% § Volatilité 100% passe de 26% à 30% § Volatilité 140% passe de 22% à 28% § CAC progresse de +15%
 Étude de cas n° 1 : BMTN indexé CAC § Secondaire : valorisation du BMTN indexé Cac § Valorisation BMTN
Étude de cas n° 1 : BMTN indexé CAC § Secondaire : valorisation du BMTN indexé Cac § Valorisation BMTN
 Étude de cas n° 1 : BMTN indexé CAC § Secondaire : valorisation du BMTN indexé Cac § Valorisation BMTN
Étude de cas n° 1 : BMTN indexé CAC § Secondaire : valorisation du BMTN indexé Cac § Valorisation BMTN
 Étude de cas n° 2 BLAC
Étude de cas n° 2 BLAC
 Etude de cas n° 2: BLAC
Etude de cas n° 2: BLAC
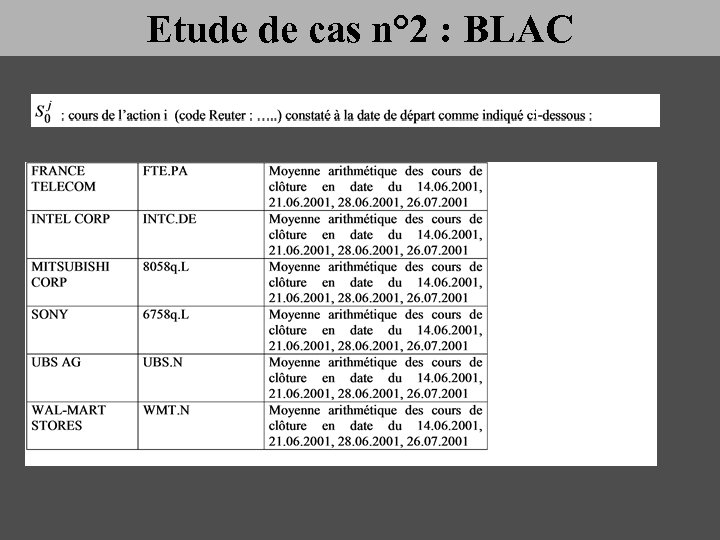 Etude de cas n° 2 : BLAC
Etude de cas n° 2 : BLAC
 Etude de cas n° 2 : BLAC Analyse du produit : Commentaire sur la condition Le cours de l’action j est toujours supérieur ou égal à la Barrière Cette condition doit être vérifiée pour toutes les actions j Cette condition doit aussi être vérifiée chaque année i Commentaire sur la condition Le cours de l’action j est inférieur (strictement) à la Barrière pendant la période d’observation i Cette condition doit être vérifiée pour au moins 2 actions j Cette condition doit aussi être vérifiée chaque année i
Etude de cas n° 2 : BLAC Analyse du produit : Commentaire sur la condition Le cours de l’action j est toujours supérieur ou égal à la Barrière Cette condition doit être vérifiée pour toutes les actions j Cette condition doit aussi être vérifiée chaque année i Commentaire sur la condition Le cours de l’action j est inférieur (strictement) à la Barrière pendant la période d’observation i Cette condition doit être vérifiée pour au moins 2 actions j Cette condition doit aussi être vérifiée chaque année i
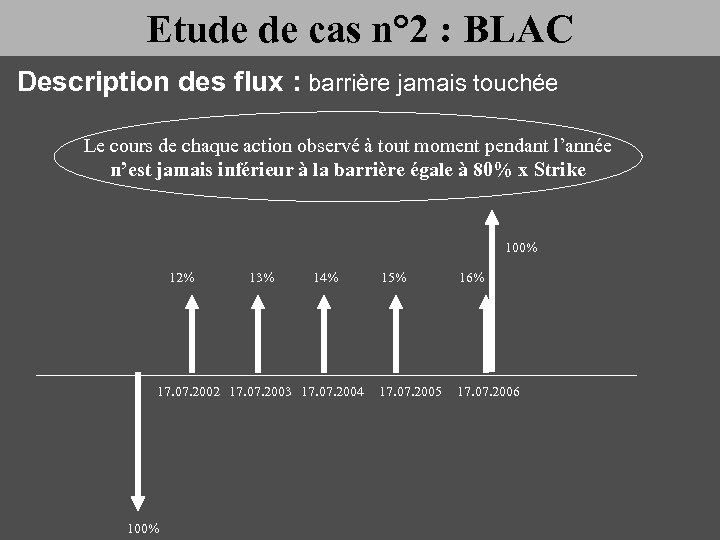 Etude de cas n° 2 : BLAC Description des flux : barrière jamais touchée Le cours de chaque action observé à tout moment pendant l’année n’est jamais inférieur à la barrière égale à 80% x Strike 100% 12% 13% 14% 17. 07. 2002 17. 07. 2003 17. 07. 2004 100% 15% 16% 17. 07. 2005 17. 07. 2006
Etude de cas n° 2 : BLAC Description des flux : barrière jamais touchée Le cours de chaque action observé à tout moment pendant l’année n’est jamais inférieur à la barrière égale à 80% x Strike 100% 12% 13% 14% 17. 07. 2002 17. 07. 2003 17. 07. 2004 100% 15% 16% 17. 07. 2005 17. 07. 2006
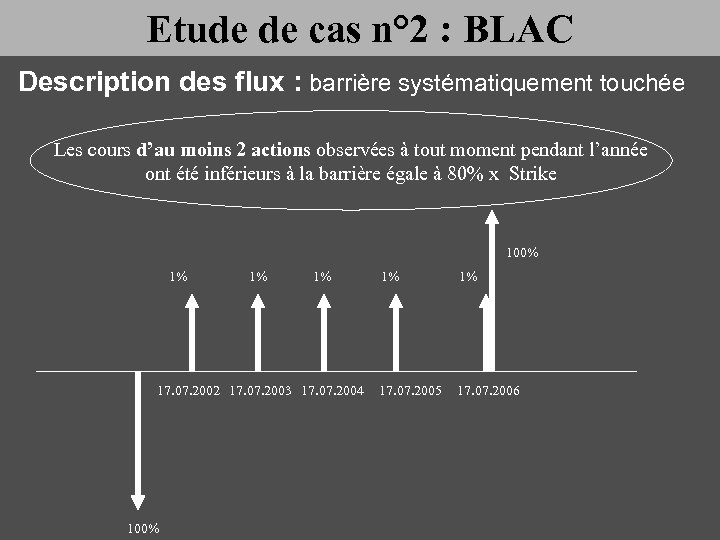 Etude de cas n° 2 : BLAC Description des flux : barrière systématiquement touchée Les cours d’au moins 2 actions observées à tout moment pendant l’année ont été inférieurs à la barrière égale à 80% x Strike 100% 1% 17. 07. 2002 17. 07. 2003 17. 07. 2004 100% 1% 1% 17. 07. 2005 17. 07. 2006
Etude de cas n° 2 : BLAC Description des flux : barrière systématiquement touchée Les cours d’au moins 2 actions observées à tout moment pendant l’année ont été inférieurs à la barrière égale à 80% x Strike 100% 1% 17. 07. 2002 17. 07. 2003 17. 07. 2004 100% 1% 1% 17. 07. 2005 17. 07. 2006
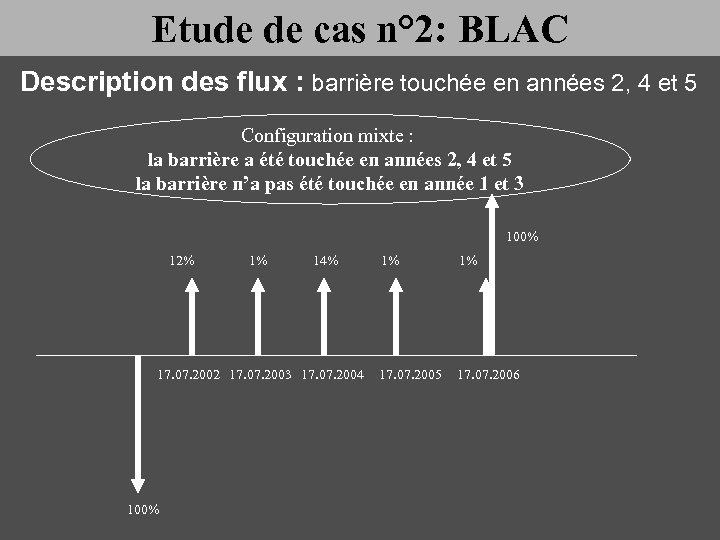 Etude de cas n° 2: BLAC Description des flux : barrière touchée en années 2, 4 et 5 Configuration mixte : la barrière a été touchée en années 2, 4 et 5 la barrière n’a pas été touchée en année 1 et 3 100% 12% 1% 14% 17. 07. 2002 17. 07. 2003 17. 07. 2004 100% 1% 1% 17. 07. 2005 17. 07. 2006
Etude de cas n° 2: BLAC Description des flux : barrière touchée en années 2, 4 et 5 Configuration mixte : la barrière a été touchée en années 2, 4 et 5 la barrière n’a pas été touchée en année 1 et 3 100% 12% 1% 14% 17. 07. 2002 17. 07. 2003 17. 07. 2004 100% 1% 1% 17. 07. 2005 17. 07. 2006
 Synthèse des formules importantes
Synthèse des formules importantes
 Synthèse des formules importantes § Cours action forward de maturité T
Synthèse des formules importantes § Cours action forward de maturité T
 Synthèse des formules importantes § Processus stochastique appliqué au cours de l’action § Loi de probabilité associée au cours de l’action à une date t
Synthèse des formules importantes § Processus stochastique appliqué au cours de l’action § Loi de probabilité associée au cours de l’action à une date t
 Synthèse des formules importantes § Prime Call « at the money forward » § Pricing de la garantie par la méthode des zéro-coupon
Synthèse des formules importantes § Prime Call « at the money forward » § Pricing de la garantie par la méthode des zéro-coupon
 Synthèse des formules importantes § Pricing d’un produit structuré à capital garanti
Synthèse des formules importantes § Pricing d’un produit structuré à capital garanti


