Product Variety under Monopoly 1 Introduction n

Product Variety under Monopoly 1

Introduction n n Most firms sell more than one product Products are differentiated in different ways q horizontally n goods of similar quality targeted at consumers of different types q q how is variety determined? is there too much variety ECO 171 2

Horizontal product differentiation n Suppose that consumers differ in their tastes q firm has to decide how best to serve different types of consumer q offer products with different characteristics but similar qualities This is horizontal product differentiation q firm designs products that appeal to different types of consumer q products are of (roughly) similar quality Questions: q how many products? q of what type? q how do we model this problem? ECO 171 3

A spatial approach to product variety n The spatial model (Hotelling) is useful to consider q q q n pricing design variety Has a much richer application as a model of product differentiation q “location” can be thought of in n q space (geography) time (departure times of planes, buses, trains) product characteristics (design and variety) consumers prefer products that are “close” to their preferred types in space, or time or characteristics ECO 171 4

An example of product variety Mc. Donald’s Burger King ECO 171 Wendy’s 5

A Spatial approach to product variety 2 n n n Assume N consumers living equally spaced along Montana Street – 1 mile long. Monopolist must decide how best to supply these consumers Consumers buy exactly one unit provided that price plus transport costs is less than V. Consumers incur there-and-back transport costs of t per mile The monopolist operates one shop q reasonable to expect that this is located at the center of Montana ECO 171 6

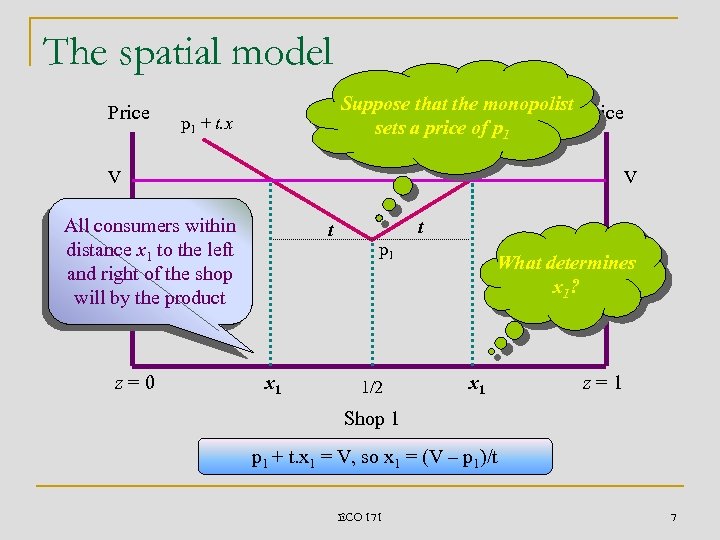The spatial model Price Suppose that the monopolist Price p sets a price of p 1 + t. x 1 p 1 + t. x V V All consumers within distance x 1 to the left and right of the shop will by the product z=0 t x 1 t p 1 1/2 What determines x 1? x 1 z=1 Shop 1 + t. x 1 = V, so x 1 = (V – p 1)/t ECO 171 7

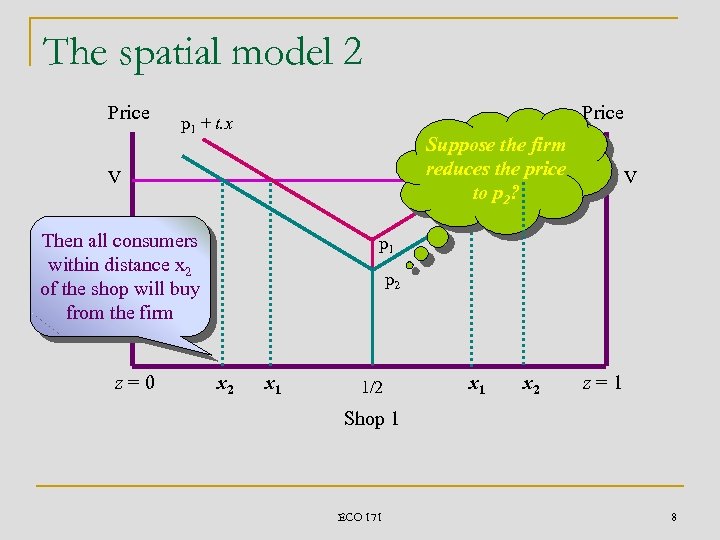The spatial model 2 Price p 1 + t. x Suppose the firm reduces the price to p 2? V Then all consumers within distance x 2 of the shop will buy from the firm z=0 Price V p 1 p 2 x 1 1/2 x 1 x 2 z=1 Shop 1 ECO 171 8

The spatial model 3 n Suppose that all consumers are to be served at price p. q q n n n The highest price is that charged to the consumers at the ends of the market Their transport costs are t/2 : since they travel ½ mile to the shop So they pay p + t/2 which must be no greater than V. So p = V – t/2. Suppose that marginal costs are c per unit. Suppose also that a shop has set-up costs of F. Then profit is p(N, 1) = N(V – t/2 – c) – F. ECO 171 9

Monopoly pricing in the spatial model n n n What if there are two shops? The monopolist will coordinate prices at the two shops With identical costs and symmetric locations, these prices will be equal: p 1 = p 2 = p q q Where should they be located? What is the optimal price p*? ECO 171 10

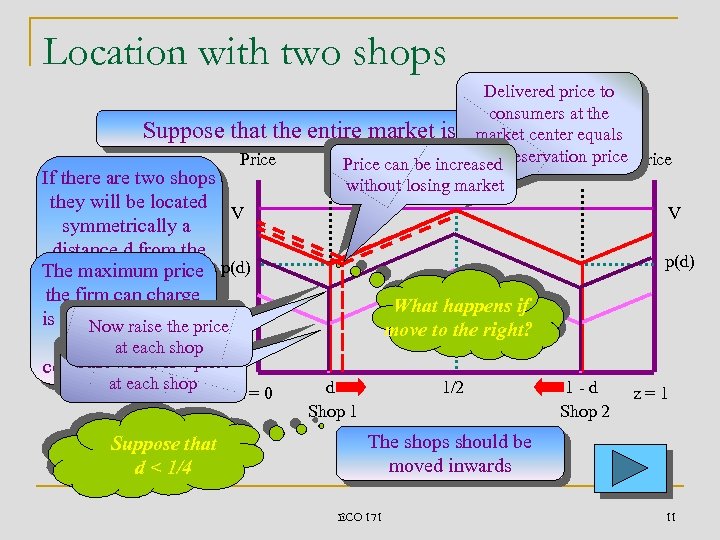Location with two shops Suppose that the Price If there are two shops they will be located V symmetrically a distance d from the The maximum price p(d) end-points of the firm can charge market is determined by the Now raise the price consumers at the at each shop Start with market center of the a low price at each shop Suppose that d < 1/4 z=0 Delivered price to consumers at the entire market is to be servedequals market center their Price can be increased reservation price Price without losing market V p(d) What happens if move to the right? d Shop 1 1/2 1 -d Shop 2 z=1 The shops should be moved inwards ECO 171 11

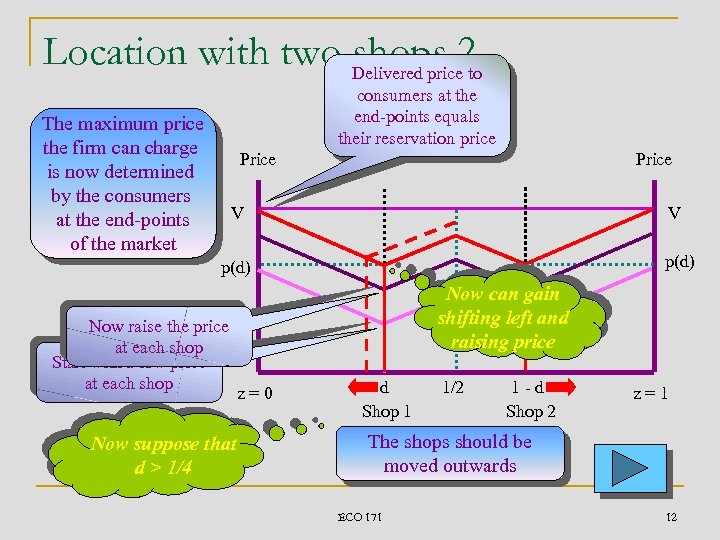Location with two Delivered price 2 shops to consumers at the end-points equals their reservation price The maximum price the firm can charge is now determined by the consumers at the end-points of the market Price V V p(d) Now raise the price at each shop Start with a low price at each shop Now suppose that d > 1/4 Now can gain shifting left and raising price z=0 d Shop 1 1/2 1 -d Shop 2 z=1 The shops should be moved outwards ECO 171 12

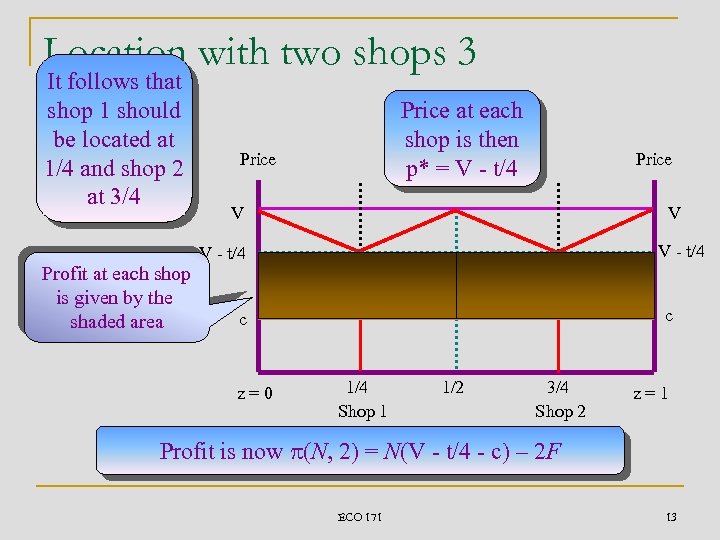Location with two shops 3 It follows that shop 1 should be located at 1/4 and shop 2 at 3/4 Price at each shop is then p* = V - t/4 Price V V V - t/4 Profit at each shop is given by the shaded area c c z=0 1/4 Shop 1 1/2 3/4 Shop 2 z=1 Profit is now p(N, 2) = N(V - t/4 - c) – 2 F ECO 171 13

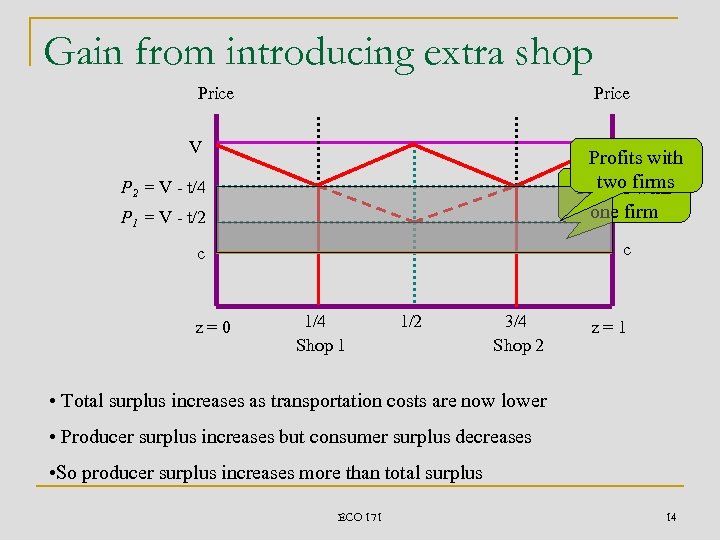Gain from introducing extra shop Price V V Profits with two - t/4 V with Profits firms one firm P 2 = V - t/4 P 1 = V - t/2 c c z=0 1/4 Shop 1 1/2 3/4 Shop 2 z=1 • Total surplus increases as transportation costs are now lower • Producer surplus increases but consumer surplus decreases • So producer surplus increases more than total surplus ECO 171 14

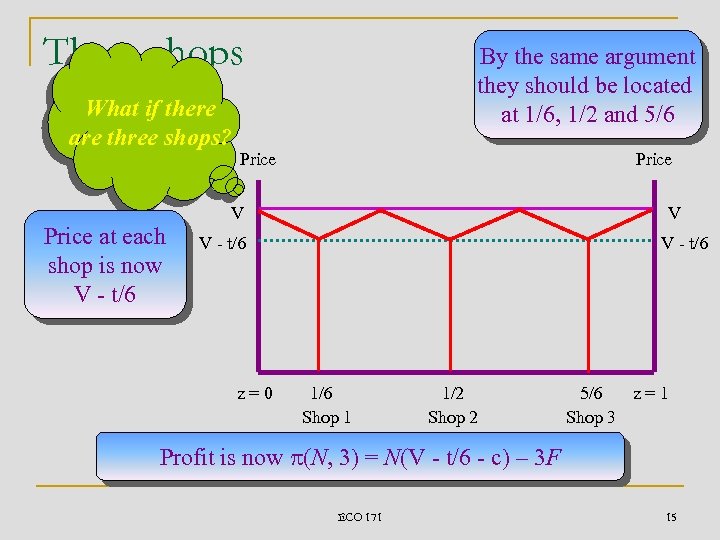Three shops What if there are three shops? Price at each shop is now V - t/6 By the same argument they should be located at 1/6, 1/2 and 5/6 Price V V V - t/6 z=0 V - t/6 1/6 Shop 1 1/2 Shop 2 5/6 z=1 Shop 3 Profit is now p(N, 3) = N(V - t/6 - c) – 3 F ECO 171 15

Optimal number of shops n A consistent pattern is emerging. • • Assume that there are n shops. They will be symmetrically located distance 1/n apart. We have already considered n = 2 and n = 3. How many shops should When n = 2 we have p(N, 2) = V - t/4 there be? • When n = 3 we have p(N, 3) = V - t/6 • It follows that p(N, n) = V - t/2 n • Aggregate profit is then p(N, n) = N(V - t/2 n - c) – n. F ECO 171 16

Optimal number of shops 2 Profit from n shops is p(N, n) = (V - t/2 n - c)N - n. F and the profit from having n + 1 shops is: p*(N, n+1) = (V - t/2(n + 1)-c)N - (n + 1)F Adding the (n +1)th shop is profitable if p(N, n+1) - p(N, n) > 0 This requires t. N/2 n - t. N/2(n + 1) > F which requires that n(n + 1) < t. N/2 F. ECO 171 17

An example Suppose that F = $50, 000 , N = 5 million and t = $1 Then t. N/2 F = 50 For an additional shop to be profitable we need n(n + 1) < 50. This is true for n < 6 There should be no more than seven shops in this case: if n = 6 then adding one more shop is profitable. But if n = 7 then adding another shop is unprofitable. ECO 171 18

Some intuition n n What does the condition on n tell us? Simply, we should expect to find greater product variety when: q q q there are many consumers. set-up costs of increasing product variety are low. consumers have strong preferences over product characteristics and differ in these n consumers are unwilling to buy a product if it is not “very close” to their most preferred product ECO 171 19

How much of the market to supply n Should the whole market be served? q Suppose not. Then each shop has a local monopoly Each shop sells to consumers within distance r q How is r determined? q n n n n q q it must be that p + tr = V so r = (V – p)/t so total demand is 2 N(V – p)/t profit to each shop is then p = 2 N(p – c)(V – p)/t – F differentiate with respect to p and set to zero: dp/dp = 2 N(V – 2 p + c)/t = 0 So the optimal price at each shop is p* = (V + c)/2 If all consumers are served price is p(N, n) = V – t/2 n Only part of the market should be served if p(N, n) < p* This implies that V < c + t/n. ECO 171 20

Partial market supply n n n If c + t/n > V supply only part of the market and set price p* = (V + c)/2 If c + t/n < V supply the whole market and set price p(N, n) = V – t/2 n Supply only part of the market: q q if the consumer reservation price is low relative to marginal production costs and transport costs if there are very few outlets ECO 171 21

Market density and prices n n What should this model imply of market prices and density? Higher density is equivalent in this model to reducing transportation cost: q q n If consumers are concentrated in half the interval, can reach the same fraction of the consumers at half the cost. Same effect as if transportation cost were cut in two Implications for prices? ECO 171 22

Market density and prices n n n From previous slides, the number of firms n is approximately determined by: n(n + 1) = t. N/2 F. As t decreases n goes down From the equation above, t/n is proportional to (n + 1). So as n decreases, t/n must decrease. Optimal price is given by p(N, n) = V – t/2 n. This decreases as t/n increases. ECO 171 23

Social optimum Are there too many shops or What number of shops maximizes total surplus? too few? Total surplus is consumer surplus profit Consumer surplus is total willingness to pay minus total revenue Profit is total revenue minus total cost Total surplus is then total willingness to pay minus total costs Total willingness to pay by consumers is N. V Total surplus is therefore N. V - Total Cost So what is Total Cost? ECO 171 24

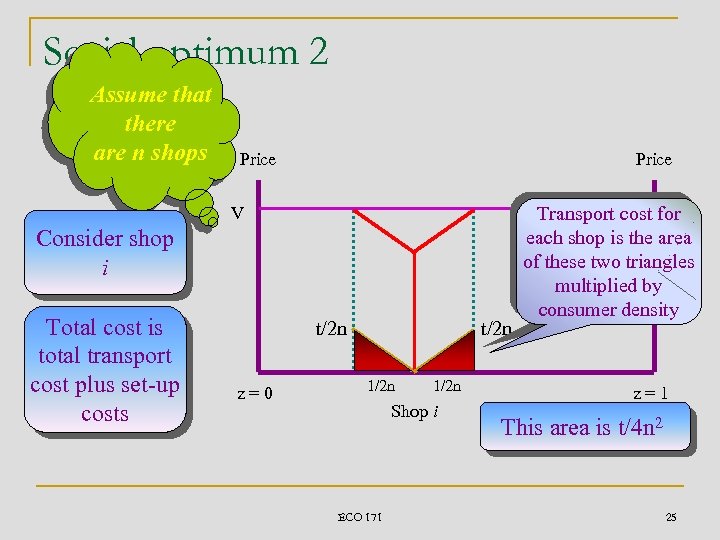Social optimum 2 Assume that there are n shops Price V Consider shop i Total cost is total transport cost plus set-up costs t/2 n z=0 t/2 n 1/2 n Shop i ECO 171 V Transport cost for each shop is the area of these two triangles multiplied by consumer density z=1 This area is t/4 n 2 25

Social optimum 3 Total cost with n shops is, therefore: C(N, n) = n(t/4 n 2)N + n. F = t. N/4 n + n. F If t = $1, F = $50, 000, Total cost with n + 1 shops is: C(N, n+1) = t. N/4(n+1)+fivethis There 5 should be (n+1). F N = million then shops: with. C(N, n adding us n = 4 + tells another Adding another shop is socially efficient ifcondition 1) < C(N, n) shop is efficient that n(n+1) < 25 This requires that t. N/4 n - t. N/4(n+1) > F which implies that n(n + 1) < t. N/4 F The monopolist operates too many shops and, more generally, provides too much product variety ECO 171 26

Optimal variety and monopoly n n n In previous example get excess variety Social value of increase in varieties < increase in monopoly profits What is the key ingredient? Variety makes markets more homogeneous Monopoly is able to extract higher surplus Is this always true? ECO 171 27

Example 1: Excess variety n n n 3 consumers: {b, g, s} 3 possible goods: bitter (B), generic(G), sweet(S) Preferences: Mc=0 Offer generic only: q p=2, p=6 Offer (B, S) q p. B = p. G = 3 q p = 9 b g s B 3 3 1 G 2 3 2 S 1 3 3 • Profits increase by 3 • Total surplus increases by 2 • CS decreases by 1 (for g) • Suppose additional investment to offer both brands: 2

Example 2: Too little variety n n n B 3 2 1 1 G 2 2 S 1 1 2 3 4 consumers: {b, gs, s} b 3 possible goods: bitter (B), gb generic(G), sweet(S) Preferences: gs Mc=0 s Offer generic only: • Profits do not increase q p=2, p=8 • CS increases by 2 Offer (B, S) • Suppose additional investment to offer both brands: 0

Product variety and price discrimination n Suppose that the monopolist delivers the product. q n What pricing policy to adopt? q q n then it is possible to price discriminate charge every consumer his reservation price V the firm pays the transport costs this is uniform delivered pricing it is discriminatory because price does not reflect costs Should every consumer be supplied? q q q suppose that there are n shops evenly spaced on Main Street cost to the most distant consumer is c + t/2 n supply this consumer so long as V (revenue) > c + t/2 n This is a weaker condition than without price discrimination. Price discrimination allows more consumers to be served. ECO 171 30

Product variety and price discrimination 2 n How many shops should the monopolist operate now? Suppose that the monopolist has n shops and is supplying the entire market. Total revenue minus production costs is N. V – N. c Total transport costs plus set-up costs is C(N, n)=t. N/4 n + n. F So profit is p(N, n) = N. V – N. c – C(N, n) But then maximizing profit means minimizing C(N, n) The discriminating monopolist operates the socially optimal number of shops. ECO 171 31