14 Процессы перехода к равновесию.pptx
- Количество слайдов: 53
 ПРОЦЕССЫ ПЕРЕХОДА К РАВНОВЕСИЮ 1
ПРОЦЕССЫ ПЕРЕХОДА К РАВНОВЕСИЮ 1
 Процессы перехода к равновесию Диффузия Тело, взаимодействующее со средой, меняет свое состояние так, чтобы прийти в равновесие с окружающими телами. Состояние тела при этом меняется: его внутренняя энергия стремится к минимуму, а энтропия возрастает и становится максимальной тогда, когда равновесие устанавливается. Эти две тенденции обычно противоре чивы и поэтому трудно предсказать явление тогда, когда способны изменяться и энергия, и энтропия. 2
Процессы перехода к равновесию Диффузия Тело, взаимодействующее со средой, меняет свое состояние так, чтобы прийти в равновесие с окружающими телами. Состояние тела при этом меняется: его внутренняя энергия стремится к минимуму, а энтропия возрастает и становится максимальной тогда, когда равновесие устанавливается. Эти две тенденции обычно противоре чивы и поэтому трудно предсказать явление тогда, когда способны изменяться и энергия, и энтропия. 2
 Процессы перехода к равновесию Диффузия Мы рассмотрим яв ления диффузии, теплопроводности и внутреннего трения, проис ходящие в замкнутых системах. Иначе говоря, речь идет о вырав нивании концентрации, температур и скоростей одних частей тела по отношению к другим (последнее, разумеется, имеет значение лишь для жидких и газообразных тел). Так как энергия в таких системах меняться не может, то переход в состояние равновесия состоит лишь в возрастании энтропии. 3
Процессы перехода к равновесию Диффузия Мы рассмотрим яв ления диффузии, теплопроводности и внутреннего трения, проис ходящие в замкнутых системах. Иначе говоря, речь идет о вырав нивании концентрации, температур и скоростей одних частей тела по отношению к другим (последнее, разумеется, имеет значение лишь для жидких и газообразных тел). Так как энергия в таких системах меняться не может, то переход в состояние равновесия состоит лишь в возрастании энтропии. 3
 Процессы перехода к равновесию Диффузия Основные законы явлений диффузии, теплопроводности и вну треннего трения весьма похожи. Начнем их рассмотрение с процес сов диффузии. С одинаковым успехом можно говорить о выравни вании концентрации газа или раствора. Наши рассуждения спра ведливы даже для твердых растворов, так как и в этом случае стремление к максимуму энтропии заставляет атомы или мо лекулы вещества перемешиваться, с тем чтобы одинаковая концен трация установилась во всех частях тела. 4
Процессы перехода к равновесию Диффузия Основные законы явлений диффузии, теплопроводности и вну треннего трения весьма похожи. Начнем их рассмотрение с процес сов диффузии. С одинаковым успехом можно говорить о выравни вании концентрации газа или раствора. Наши рассуждения спра ведливы даже для твердых растворов, так как и в этом случае стремление к максимуму энтропии заставляет атомы или мо лекулы вещества перемешиваться, с тем чтобы одинаковая концен трация установилась во всех частях тела. 4
 Процессы перехода к равновесию Диффузия • 5
Процессы перехода к равновесию Диффузия • 5
 Процессы перехода к равновесию Диффузия • 6
Процессы перехода к равновесию Диффузия • 6
 Процессы перехода к равновесию Диффузия Молекулы движутся беспорядочно, во все стороны, в том числе и в сторону большей концентрации, но вероятность перемещения молекул в «правильную» сторону больше. Это значит, что через мысленную площадку, поставленную поперек потока, больше частиц перейдет со стороны большей концентрации к меньшей, чем наоборот. 7
Процессы перехода к равновесию Диффузия Молекулы движутся беспорядочно, во все стороны, в том числе и в сторону большей концентрации, но вероятность перемещения молекул в «правильную» сторону больше. Это значит, что через мысленную площадку, поставленную поперек потока, больше частиц перейдет со стороны большей концентрации к меньшей, чем наоборот. 7
 Процессы перехода к равновесию Диффузия • 8
Процессы перехода к равновесию Диффузия • 8
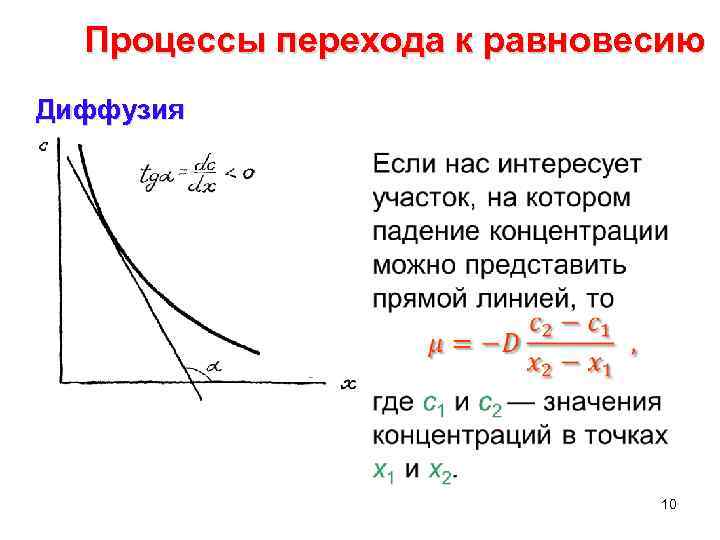
 Процессы перехода к равновесию Диффузия Концентрация и поток массы должны измеряться в соответ ствующих единицах. Если концентрация измеряется в граммах на см 3, то поток должен измеряться в граммах через см 2 в 1 с. От сюда видно, что коэффициент диффузии должен иметь вполне опре деленную размерность, в системе И С он будет измеряться в м 2/с. Падение концентрации происходит обычно по провисающей кри вой, риведенной на п следующем слайде. 9
Процессы перехода к равновесию Диффузия Концентрация и поток массы должны измеряться в соответ ствующих единицах. Если концентрация измеряется в граммах на см 3, то поток должен измеряться в граммах через см 2 в 1 с. От сюда видно, что коэффициент диффузии должен иметь вполне опре деленную размерность, в системе И С он будет измеряться в м 2/с. Падение концентрации происходит обычно по провисающей кри вой, риведенной на п следующем слайде. 9
 Процессы перехода к равновесию Диффузия • 10
Процессы перехода к равновесию Диффузия • 10
 Процессы перехода к равновесию Теплопроводность и вязкость • 11
Процессы перехода к равновесию Теплопроводность и вязкость • 11
 Процессы перехода к равновесию Теплопроводность и вязкость Оно носит название градиен та температуры. При выравнивании температур участки тела с большей энергией уменьшают ее, участки тела с меньшей энергией получают тепло от более богатых участков. В каком то условном смысле тепло «пере текает» из одного участка в другой. Количество тепла, переходящее из одного участка тепла в другой через площадку раздела размером в единицу площади за единицу времени, носит название теплового потока q. 12
Процессы перехода к равновесию Теплопроводность и вязкость Оно носит название градиен та температуры. При выравнивании температур участки тела с большей энергией уменьшают ее, участки тела с меньшей энергией получают тепло от более богатых участков. В каком то условном смысле тепло «пере текает» из одного участка в другой. Количество тепла, переходящее из одного участка тепла в другой через площадку раздела размером в единицу площади за единицу времени, носит название теплового потока q. 12
 Процессы перехода к равновесию Теплопроводность и вязкость • 13
Процессы перехода к равновесию Теплопроводность и вязкость • 13
 Процессы перехода к равновесию Теплопроводность и вязкость • 14
Процессы перехода к равновесию Теплопроводность и вязкость • 14
 Процессы перехода к равновесию Теплопроводность и вязкость Третье явление того же класса состоит в выравнивании скоро стей. Если газ или жидкость движутся в каком то направлении так, что разные их слои перемещаются с разными скоростями, то такое движение является неустойчивым. Рано или поздно скорости движе ния должны выровняться: медленные слои ускорятся, а быстрые замедлятся. Это явление называют также внутренним трением, или вязкостью. Оно присуще всем телам, кроме гелия II. 15
Процессы перехода к равновесию Теплопроводность и вязкость Третье явление того же класса состоит в выравнивании скоро стей. Если газ или жидкость движутся в каком то направлении так, что разные их слои перемещаются с разными скоростями, то такое движение является неустойчивым. Рано или поздно скорости движе ния должны выровняться: медленные слои ускорятся, а быстрые замедлятся. Это явление называют также внутренним трением, или вязкостью. Оно присуще всем телам, кроме гелия II. 15
 Процессы перехода к равновесию Теплопроводность и вязкость • 16
Процессы перехода к равновесию Теплопроводность и вязкость • 16
 Процессы перехода к равновесию Теплопроводность и вязкость Для наглядности мы можем предположить, что речь идет о быстрой речке, где скорости потоков на поверхности максимальны и постепенно убывают ко дну реки. Если в какой то момент времени устранить причины, создающие движение жидкости, то скорости движения различных слоев начнут выравниваться в соответствии с законом возрастания энтропии. 17
Процессы перехода к равновесию Теплопроводность и вязкость Для наглядности мы можем предположить, что речь идет о быстрой речке, где скорости потоков на поверхности максимальны и постепенно убывают ко дну реки. Если в какой то момент времени устранить причины, создающие движение жидкости, то скорости движения различных слоев начнут выравниваться в соответствии с законом возрастания энтропии. 17
 Процессы перехода к равновесию Теплопроводность и вязкость • 18
Процессы перехода к равновесию Теплопроводность и вязкость • 18
 Процессы перехода к равновесию Быстрота выравнивания Хорошо известно, что установление равновесия может происхо дить в самые различные сроки. Температура брошенного в воду раскаленного куска железа и температура. воды уравняются очень быстро. Напротив, температуры воздуха и нагретого кирпича урав ниваются медленно. В течение мгновений продиффундирует азот в кислороде, многими днями длится выравнивание концентраций раствора медного купороса. 19
Процессы перехода к равновесию Быстрота выравнивания Хорошо известно, что установление равновесия может происхо дить в самые различные сроки. Температура брошенного в воду раскаленного куска железа и температура. воды уравняются очень быстро. Напротив, температуры воздуха и нагретого кирпича урав ниваются медленно. В течение мгновений продиффундирует азот в кислороде, многими днями длится выравнивание концентраций раствора медного купороса. 19
 Процессы перехода к равновесию Быстрота выравнивания Также и выравнивание скоростей может происходить в резко отличные времена, смотря по тому, идет ли речь о газе или о вязкой жидкости. Общей формулы в отношении времен выравнивания дать нельзя, так как на этих временах сказывается геометрия опыта. 20
Процессы перехода к равновесию Быстрота выравнивания Также и выравнивание скоростей может происходить в резко отличные времена, смотря по тому, идет ли речь о газе или о вязкой жидкости. Общей формулы в отношении времен выравнивания дать нельзя, так как на этих временах сказывается геометрия опыта. 20
 Процессы перехода к равновесию Быстрота выравнивания Остывающее тело может иметь форму цилиндра или пластинки; диффундирующий газ в начальный момент может на ходиться внутри маленького сферического объема или может быть распределен вдоль какой нибудь поверхности; внутреннее трение может наблюдаться в трубах разного сечения или в открытых водое мах. Подобные обстоятельства должны каждый раз учитываться осо бо, и расчет точных значений времен выравнивания является труд ной математической задачей. 21
Процессы перехода к равновесию Быстрота выравнивания Остывающее тело может иметь форму цилиндра или пластинки; диффундирующий газ в начальный момент может на ходиться внутри маленького сферического объема или может быть распределен вдоль какой нибудь поверхности; внутреннее трение может наблюдаться в трубах разного сечения или в открытых водое мах. Подобные обстоятельства должны каждый раз учитываться осо бо, и расчет точных значений времен выравнивания является труд ной математической задачей. 21
 Процессы перехода к равновесию Быстрота выравнивания Однако можно отвлечься от геометри ческих частностей и попытаться решить вопрос в общей форме, если отказаться от цели получить точную формулу и удовлетвориться нахождением лишь пропорциональности между физическими величинами. На этом пути помогают соображения о размер ностях физических величин, которые должны быть связаны между собой. Рассмотрим, например, явление диффузии. 22
Процессы перехода к равновесию Быстрота выравнивания Однако можно отвлечься от геометри ческих частностей и попытаться решить вопрос в общей форме, если отказаться от цели получить точную формулу и удовлетвориться нахождением лишь пропорциональности между физическими величинами. На этом пути помогают соображения о размер ностях физических величин, которые должны быть связаны между собой. Рассмотрим, например, явление диффузии. 22
 Процессы перехода к равновесию Быстрота выравнивания • 23
Процессы перехода к равновесию Быстрота выравнивания • 23
 Процессы перехода к равновесию Быстрота выравнивания • 24
Процессы перехода к равновесию Быстрота выравнивания • 24
 Процессы перехода к равновесию Быстрота выравнивания где const — постоянная безразмерная величина, const зависящая от гео метрических условий задачи. Величина L, от квадрата которой за висит скорость выравнивания концентрации, имеет смысл геометри ческого размера области, в которой происходит выравнивание. Зна чит, если концентрация в пределах одного сантиметра выравнивает ся, скажем, за 10 с , то в пределах двух сантиметров она выравнива ется за 40 с. 25
Процессы перехода к равновесию Быстрота выравнивания где const — постоянная безразмерная величина, const зависящая от гео метрических условий задачи. Величина L, от квадрата которой за висит скорость выравнивания концентрации, имеет смысл геометри ческого размера области, в которой происходит выравнивание. Зна чит, если концентрация в пределах одного сантиметра выравнивает ся, скажем, за 10 с , то в пределах двух сантиметров она выравнива ется за 40 с. 25
 Процессы перехода к равновесию Быстрота выравнивания Таким же точно образом можно решить вопрос о выравнивании температуры. В основной закон этого явления входят количество тепла, коэффи циент теплопроводности, температура и рассто яние. Но приращение количества тепла в едини це объема может быть представлено в виде dq = rсрd. T Здесь cр – удельная теплоемкость при постоян ном давлении, r – плот ность (таким образом, рr с есть теплоемкость единицы объема). 26
Процессы перехода к равновесию Быстрота выравнивания Таким же точно образом можно решить вопрос о выравнивании температуры. В основной закон этого явления входят количество тепла, коэффи циент теплопроводности, температура и рассто яние. Но приращение количества тепла в едини це объема может быть представлено в виде dq = rсрd. T Здесь cр – удельная теплоемкость при постоян ном давлении, r – плот ность (таким образом, рr с есть теплоемкость единицы объема). 26
 Процессы перехода к равновесию Быстрота выравнивания • 27
Процессы перехода к равновесию Быстрота выравнивания • 27
 Процессы перехода к равновесию Быстрота выравнивания • 28
Процессы перехода к равновесию Быстрота выравнивания • 28
 Процессы перехода к равновесию Быстрота выравнивания Коэффициенты диф фузии и температуропроводности имеют одинаковую размерность и вполне аналогичны в рассмотренных двух явлениях выравнивания. Мы видим, чем определяется остывание тела. Процесс идет тем медленнее, чем больше плотность и теплоемкость и чем меньше коэффициент теплопроводности. 29
Процессы перехода к равновесию Быстрота выравнивания Коэффициенты диф фузии и температуропроводности имеют одинаковую размерность и вполне аналогичны в рассмотренных двух явлениях выравнивания. Мы видим, чем определяется остывание тела. Процесс идет тем медленнее, чем больше плотность и теплоемкость и чем меньше коэффициент теплопроводности. 29
 Процессы перехода к равновесию Быстрота выравнивания Как и для диффузии, для выравнивания температур характерна зависимость от квадрата расстояния: время выравнивания пропорционально квадрату линейного размера области. Не повторяя аналогичных рассуждений, можно записать формулу для времени выравнивания скоростей движения частей жидкости или газа. Вполне естественно, что и ей может быть придан тот же вид: 30
Процессы перехода к равновесию Быстрота выравнивания Как и для диффузии, для выравнивания температур характерна зависимость от квадрата расстояния: время выравнивания пропорционально квадрату линейного размера области. Не повторяя аналогичных рассуждений, можно записать формулу для времени выравнивания скоростей движения частей жидкости или газа. Вполне естественно, что и ей может быть придан тот же вид: 30
 Процессы перехода к равновесию Быстрота выравнивания • 31
Процессы перехода к равновесию Быстрота выравнивания • 31
 Процессы перехода к равновесию Стационарные процессы Если тело предоставлено самому себе, то различия в температу рах, концентрациях и скоростях движения частей тела обязательно уравняются в соответствии с принципом возрастания энтропии. Однако вполне возможно и такое состояние тела, при котором дли тельное время в нем существует неизменный поток тепла или ве щества или неизменное распределение скоростей движения частей тела друг по отношению к другу. Процессы такого рода носят на звание тационарных стационарных. 32 с
Процессы перехода к равновесию Стационарные процессы Если тело предоставлено самому себе, то различия в температу рах, концентрациях и скоростях движения частей тела обязательно уравняются в соответствии с принципом возрастания энтропии. Однако вполне возможно и такое состояние тела, при котором дли тельное время в нем существует неизменный поток тепла или ве щества или неизменное распределение скоростей движения частей тела друг по отношению к другу. Процессы такого рода носят на звание тационарных стационарных. 32 с
 Процессы перехода к равновесию Стационарные процессы Разумеется, при стационарном процессе тело не находится в состоянии равновесия. При каких же условиях возможны подобные процессы? Пред ставим ебе металлический стержень, к с которому с одного конца подводится в каждый момент времени некоторое количество тепла. Другой конец стержня находится в тепловом контакте с более холодным телом. 33
Процессы перехода к равновесию Стационарные процессы Разумеется, при стационарном процессе тело не находится в состоянии равновесия. При каких же условиях возможны подобные процессы? Пред ставим ебе металлический стержень, к с которому с одного конца подводится в каждый момент времени некоторое количество тепла. Другой конец стержня находится в тепловом контакте с более холодным телом. 33
 Процессы перехода к равновесию Стационарные процессы Условия, при которых температуры вдоль стерж ня не будут изменяться, т. е. условия постоянства градиента темпе ратуры на всем пути теплового потока, будут выполнены в том слу чае, когда количество тепла, отнимаемого холодным телом, будет строго равно количеству тепла, подводимому за то же время более горячим телом. 34
Процессы перехода к равновесию Стационарные процессы Условия, при которых температуры вдоль стерж ня не будут изменяться, т. е. условия постоянства градиента темпе ратуры на всем пути теплового потока, будут выполнены в том слу чае, когда количество тепла, отнимаемого холодным телом, будет строго равно количеству тепла, подводимому за то же время более горячим телом. 34
 Процессы перехода к равновесию Стационарные процессы При аналогичных условиях возможен и стационар ный диффузионный процесс. Для его создания необходимо в одном месте подводить, а в другом уводить из тела равные количества ве щества, поддерживая, таким образом, неизменной определенную разность концентраций между двумя участками тела. 35
Процессы перехода к равновесию Стационарные процессы При аналогичных условиях возможен и стационар ный диффузионный процесс. Для его создания необходимо в одном месте подводить, а в другом уводить из тела равные количества ве щества, поддерживая, таким образом, неизменной определенную разность концентраций между двумя участками тела. 35
 Процессы перехода к равновесию Стационарные процессы Стационарный вязкостный процесс может быть осуществлен, на пример, в пространстве между двумя коаксиальными цилиндрами, вращающимися с разными скоростями. Так как у твердых поверхно стей жидкость или газ будут иметь скорость, совпадающую с дви жением твердой стенки, то внутри жидкости создастся постоянный перепад скоростей. 36
Процессы перехода к равновесию Стационарные процессы Стационарный вязкостный процесс может быть осуществлен, на пример, в пространстве между двумя коаксиальными цилиндрами, вращающимися с разными скоростями. Так как у твердых поверхно стей жидкость или газ будут иметь скорость, совпадающую с дви жением твердой стенки, то внутри жидкости создастся постоянный перепад скоростей. 36
 Процессы перехода к равновесию Стационарные процессы Стационарный процесс возникает не сразу. В течение какого то времени происходит установление этого процесса. Представим себе, что стержень, по которому передается тепло, погружен одним концом в снег. В начальный момент времени тем пература стержня во всех его точках равна нулю. Если теперь при вести другой конец стержня в епловой т контакт с кипящей водой, то темпера тура начнет повышаться во всех точках стержня, причем, 37 разумеется, не одинаково быстро.
Процессы перехода к равновесию Стационарные процессы Стационарный процесс возникает не сразу. В течение какого то времени происходит установление этого процесса. Представим себе, что стержень, по которому передается тепло, погружен одним концом в снег. В начальный момент времени тем пература стержня во всех его точках равна нулю. Если теперь при вести другой конец стержня в епловой т контакт с кипящей водой, то темпера тура начнет повышаться во всех точках стержня, причем, 37 разумеется, не одинаково быстро.
 Процессы перехода к равновесию Стационарные процессы Почти сразу установится высокая температура на конце стержня, приведенном в контакт с кипящей водой. Медленнее всего будет расти температура на конце стержня, погруженном в снег. Через некоторое время рост температуры во всех точках стержня прекратится, установится вполне определен ное распределение температуры — процесс станет стационарным. Характер распределения температур зависит от того, сколько теп ла подводится (отводится) в единицу времени. 38
Процессы перехода к равновесию Стационарные процессы Почти сразу установится высокая температура на конце стержня, приведенном в контакт с кипящей водой. Медленнее всего будет расти температура на конце стержня, погруженном в снег. Через некоторое время рост температуры во всех точках стержня прекратится, установится вполне определен ное распределение температуры — процесс станет стационарным. Характер распределения температур зависит от того, сколько теп ла подводится (отводится) в единицу времени. 38
 Процессы перехода к равновесию Стационарные процессы В электрическом утюге, нагреваемом спиралью, центральная часть находится при самой высокой температуре, далее температура постепенно падает к наружным краям. В окружающей среде, ко нечно, наиболее горячим является воздух, примыкающий к утюгу. Далее температура спадает более быстро в силу малой теплопровод ности воздуха. 39
Процессы перехода к равновесию Стационарные процессы В электрическом утюге, нагреваемом спиралью, центральная часть находится при самой высокой температуре, далее температура постепенно падает к наружным краям. В окружающей среде, ко нечно, наиболее горячим является воздух, примыкающий к утюгу. Далее температура спадает более быстро в силу малой теплопровод ности воздуха. 39
 Процессы перехода к равновесию Стационарные процессы Для грубых расчетов и при малом размере тела, находящегося в воздухе или жидкости, можно не рассматривать кривой падения температуры, а говорить о разнице между температурой тела и среды, Т – Т 0. Тепловой поток, передаваемый телом в среду за единицу вре мени, можно в этом случае полагать пропорциональным этой разности температур: q = k(T – T 0). 40
Процессы перехода к равновесию Стационарные процессы Для грубых расчетов и при малом размере тела, находящегося в воздухе или жидкости, можно не рассматривать кривой падения температуры, а говорить о разнице между температурой тела и среды, Т – Т 0. Тепловой поток, передаваемый телом в среду за единицу вре мени, можно в этом случае полагать пропорциональным этой разности температур: q = k(T – T 0). 40
 Процессы перехода к равновесию Стационарные процессы Коэффициент k называется коэффициентом теплоотдачи. Это важная для техники величина. теплоотдачи Ее значения и вычисления, с ней связанные, обсуждаются в курсе теплотехники. Обозначим через Р мощность, подводимую к телу, например элек трическую мощность в случае утюга. Условие стационарности процесса требует равенства P = k(T – T 0). 41
Процессы перехода к равновесию Стационарные процессы Коэффициент k называется коэффициентом теплоотдачи. Это важная для техники величина. теплоотдачи Ее значения и вычисления, с ней связанные, обсуждаются в курсе теплотехники. Обозначим через Р мощность, подводимую к телу, например элек трическую мощность в случае утюга. Условие стационарности процесса требует равенства P = k(T – T 0). 41
 Процессы перехода к равновесию Стационарные процессы • 42
Процессы перехода к равновесию Стационарные процессы • 42
 Процессы перехода к равновесию Стационарные процессы В зависимости от значения коэффициента теплоотдачи тер мометр, лежащий под солнечными лучами, может показать в пол ном смысле слова все, что угодно. Измеренная при таких условиях температура есть температура термометра и ни в какой степени не характеризует погоду. Аналогичные рассуждения можно провести и в отношении диффузии. 43
Процессы перехода к равновесию Стационарные процессы В зависимости от значения коэффициента теплоотдачи тер мометр, лежащий под солнечными лучами, может показать в пол ном смысле слова все, что угодно. Измеренная при таких условиях температура есть температура термометра и ни в какой степени не характеризует погоду. Аналогичные рассуждения можно провести и в отношении диффузии. 43
 Процессы перехода к равновесию Движение в вязкой среде Соображения, касающиеся размерности физических величин, по могают в решении задач огромной практической важности, например задачи о стационарном обтекании жидкостью или газом препятствия, или, что то же самое, о движении тела в среде. Наиболее важной проблемой является вопрос о силе сопротивле ния, испытываемой телом при движении в среде. 44
Процессы перехода к равновесию Движение в вязкой среде Соображения, касающиеся размерности физических величин, по могают в решении задач огромной практической важности, например задачи о стационарном обтекании жидкостью или газом препятствия, или, что то же самое, о движении тела в среде. Наиболее важной проблемой является вопрос о силе сопротивле ния, испытываемой телом при движении в среде. 44
 Процессы перехода к равновесию Движение в вязкой среде Эта сила сопротив ления может зависеть от размеров тела L, скорости движения тела и и свойств жидкости (или газа), а именно, его плотности ρ и вязко сти . Другие величины не η должны играть роли в этом процессе. Подберем сначала безразмерную величину, составленную из L, и, ρ и η. Кинематическая, вязкость n =η/ρ имеет размерность L 2 T 1 , но такую же размерность имеет и произве дение u Lu. L 45
Процессы перехода к равновесию Движение в вязкой среде Эта сила сопротив ления может зависеть от размеров тела L, скорости движения тела и и свойств жидкости (или газа), а именно, его плотности ρ и вязко сти . Другие величины не η должны играть роли в этом процессе. Подберем сначала безразмерную величину, составленную из L, и, ρ и η. Кинематическая, вязкость n =η/ρ имеет размерность L 2 T 1 , но такую же размерность имеет и произве дение u Lu. L 45
 Процессы перехода к равновесию Движение в вязкой среде • 46
Процессы перехода к равновесию Движение в вязкой среде • 46
 Процессы перехода к равновесию Движение в вязкой среде Если движения разных тел в разных жидкостях приводят к одному и тому же значению Re, то Re такие движения называют по добными. Существует большая техническая дисциплина – теория подобия, в которой выводы об особенностях явления делаются на основании наблюдения подобного явления, осуществленного на модели. 47
Процессы перехода к равновесию Движение в вязкой среде Если движения разных тел в разных жидкостях приводят к одному и тому же значению Re, то Re такие движения называют по добными. Существует большая техническая дисциплина – теория подобия, в которой выводы об особенностях явления делаются на основании наблюдения подобного явления, осуществленного на модели. 47
 Процессы перехода к равновесию Движение в вязкой среде Вернемся теперь к поставленной задаче: отыскать выражение силы сопротивления, испытываемой телом, движущимся в среде. Размерность силы есть MLT 2. Выразим ее через размерность тех величин, которыми мы оперируем, так как больше она ни от чего не может зависеть. Тогда MLT 2=[r]a [u]b[L]g[ ]d, 48
Процессы перехода к равновесию Движение в вязкой среде Вернемся теперь к поставленной задаче: отыскать выражение силы сопротивления, испытываемой телом, движущимся в среде. Размерность силы есть MLT 2. Выразим ее через размерность тех величин, которыми мы оперируем, так как больше она ни от чего не может зависеть. Тогда MLT 2=[r]a [u]b[L]g[ ]d, 48
 Процессы перехода к равновесию Движение в вязкой среде т. е. MLT 2= Ma. L 3 a. Lb. T b Lg. Md. L d. T d, Значит, a+d=1, -3 a+b+g-d=1, -b-d=-2 Выражая a, b, g через d, получим a=1 -d, b=2 -b, g=2 -b. -b Таким образом, в наиболее общем случае сила F может быть пред ставлена в виде суммы слагаемых, каждое из которых имеет найден ную 49 размерность:
Процессы перехода к равновесию Движение в вязкой среде т. е. MLT 2= Ma. L 3 a. Lb. T b Lg. Md. L d. T d, Значит, a+d=1, -3 a+b+g-d=1, -b-d=-2 Выражая a, b, g через d, получим a=1 -d, b=2 -b, g=2 -b. -b Таким образом, в наиболее общем случае сила F может быть пред ставлена в виде суммы слагаемых, каждое из которых имеет найден ную 49 размерность:
 Процессы перехода к равновесию Движение в вязкой среде • 50
Процессы перехода к равновесию Движение в вязкой среде • 50
 Процессы перехода к равновесию Движение в вязкой среде • 51
Процессы перехода к равновесию Движение в вязкой среде • 51
 Процессы перехода к равновесию Движение в вязкой среде • 52
Процессы перехода к равновесию Движение в вязкой среде • 52
 Процессы перехода к равновесию Движение в вязкой среде Благодаря интенсивному перемешиванию передача движения от слоя к слою перестает зависеть от вязкости. Это может быть лишь в том случае, если f(Re) стремится к пределу при возрастании ско рости. Поэтому при больших скоростях движения сила сопротивле ния становится пропорциональной квадрату скорости: F =const ru 2 L 2. 53
Процессы перехода к равновесию Движение в вязкой среде Благодаря интенсивному перемешиванию передача движения от слоя к слою перестает зависеть от вязкости. Это может быть лишь в том случае, если f(Re) стремится к пределу при возрастании ско рости. Поэтому при больших скоростях движения сила сопротивле ния становится пропорциональной квадрату скорости: F =const ru 2 L 2. 53


