повторение.pptx
- Количество слайдов: 59
 Процентом от числа называется сотая его часть Чтобы найти 1% от числа, необходимо данное число разделить на 100. Чтобы найти дробь (часть) от числа, нужно это число умножить на данную дробь. Чтобы найти число по его части, выраженной дробью, нужно данное число разделить на дробь. Школа Квентин – подготовка к ЕГЭ
Процентом от числа называется сотая его часть Чтобы найти 1% от числа, необходимо данное число разделить на 100. Чтобы найти дробь (часть) от числа, нужно это число умножить на данную дробь. Чтобы найти число по его части, выраженной дробью, нужно данное число разделить на дробь. Школа Квентин – подготовка к ЕГЭ
 Задание 1, тип 1: вычисления 1. ЕГЭ по физике сдавали 25 выпускников школы, что составляет треть от общего количества выпускников. Сколько выпускников этой школы не сдавали экзамен по физике? 2. Килограмм орехов стоит 75 рублей. Маша купила 4 кг 400 г орехов. Сколько рублей сдачи она должна получить с 350 рублей? 3. Поезд Казань-Москва отправляется в 21: 35, а прибывает в 10: 35 на следующий день (время московское). Сколько часов поезд находится в пути? 4. Павел Иванович купил американский автомобиль, спидометр которого показывает скорость в милях в час. Какова скорость автомобиля в километрах в час, если спидометр показывает 65 миль в час? Считайте, что 1 миля равна 1609 м. Ответ округлите до целого числа.
Задание 1, тип 1: вычисления 1. ЕГЭ по физике сдавали 25 выпускников школы, что составляет треть от общего количества выпускников. Сколько выпускников этой школы не сдавали экзамен по физике? 2. Килограмм орехов стоит 75 рублей. Маша купила 4 кг 400 г орехов. Сколько рублей сдачи она должна получить с 350 рублей? 3. Поезд Казань-Москва отправляется в 21: 35, а прибывает в 10: 35 на следующий день (время московское). Сколько часов поезд находится в пути? 4. Павел Иванович купил американский автомобиль, спидометр которого показывает скорость в милях в час. Какова скорость автомобиля в километрах в час, если спидометр показывает 65 миль в час? Считайте, что 1 миля равна 1609 м. Ответ округлите до целого числа.
 Задание 1, тип 2: Округление с недостатком 1. В обменном пункте 1 гривна стоит 3 рубля 70 копеек. Отдыхающие обменяли рубли на гривны и купили 3 кг помидоров по цене 4 гривны за 1 кг. Во сколько рублей обошлась им эта покупка? Ответ округлите до целого числа. 2. Ананасы стоят 85 руб. за штуку. Какое максимальное число ананасов можно купить на 500 руб. , если их цена снизится на 20%? 3. Сырок стоит 7 рублей 20 копеек. Какое наибольшее число сырков можно купить на 60 рублей?
Задание 1, тип 2: Округление с недостатком 1. В обменном пункте 1 гривна стоит 3 рубля 70 копеек. Отдыхающие обменяли рубли на гривны и купили 3 кг помидоров по цене 4 гривны за 1 кг. Во сколько рублей обошлась им эта покупка? Ответ округлите до целого числа. 2. Ананасы стоят 85 руб. за штуку. Какое максимальное число ананасов можно купить на 500 руб. , если их цена снизится на 20%? 3. Сырок стоит 7 рублей 20 копеек. Какое наибольшее число сырков можно купить на 60 рублей?
 Задание 1, тип 3: Округление с избытком 1. В летнем лагере на каждого участника полагается 40 г сахара в день. В лагере 181 человек. Сколько килограммовых упаковок сахара понадобится на весь лагерь на 5 дней? 2. В доме, в котором живет Петя, один подъезд. На каждом этаже находится по 6 квартир. Петя живет в квартире № 50. На каком этаже живет Петя? 3. В пачке 500 листов бумаги формата А 4. За неделю в офисе расходуется 1200 листов. Какое наименьшее количество пачек бумаги нужно купить в офис на 4 недели?
Задание 1, тип 3: Округление с избытком 1. В летнем лагере на каждого участника полагается 40 г сахара в день. В лагере 181 человек. Сколько килограммовых упаковок сахара понадобится на весь лагерь на 5 дней? 2. В доме, в котором живет Петя, один подъезд. На каждом этаже находится по 6 квартир. Петя живет в квартире № 50. На каком этаже живет Петя? 3. В пачке 500 листов бумаги формата А 4. За неделю в офисе расходуется 1200 листов. Какое наименьшее количество пачек бумаги нужно купить в офис на 4 недели?
 Задание 1, тип 4: проценты 1. Задачу № 1 правильно решили 13230 человек, что составляет 42% от выпускников города. Сколько всего выпускников в этом городе? 2. Налог на доходы составляет 13% от заработной платы. Заработная плата Ивана Кузьмича равна 12 500 рублей. Сколько рублей он получит после вычета налога на доходы? 3. Магазин делает пенсионерам скидку на определенное количество процентов от цены покупки. Пакет кефира стоит в магазине 40 рублей. Пенсионер заплатил за пакет кефира 38 рублей. Сколько процентов составляет скидка для пенсионеров?
Задание 1, тип 4: проценты 1. Задачу № 1 правильно решили 13230 человек, что составляет 42% от выпускников города. Сколько всего выпускников в этом городе? 2. Налог на доходы составляет 13% от заработной платы. Заработная плата Ивана Кузьмича равна 12 500 рублей. Сколько рублей он получит после вычета налога на доходы? 3. Магазин делает пенсионерам скидку на определенное количество процентов от цены покупки. Пакет кефира стоит в магазине 40 рублей. Пенсионер заплатил за пакет кефира 38 рублей. Сколько процентов составляет скидка для пенсионеров?
 Задание 1, тип 5: проценты и округление 1. Флакон шампуня стоит 160 рублей. Какое наибольшее число флаконов можно купить на 1000 рублей во время распродажи, когда скидка составляет 25% ? 2. Студент получил свой первый гонорар в размере 700 рублей за выполненный перевод. Он решил на все полученные деньги купить букет тюльпанов для своей учительницы английского языка. Какое наибольшее количество тюльпанов сможет купить студент, если удержанный у него налог на доходы составляет 13% гонорара, тюльпаны стоят 60 рублей за штуку и букет должен состоять из нечетного числа цветов? 3. Билет на автобус стоит 15 рублей. Какое максимальное число билетов можно будет купить на 100 рублей после повышения цены билета на 20%?
Задание 1, тип 5: проценты и округление 1. Флакон шампуня стоит 160 рублей. Какое наибольшее число флаконов можно купить на 1000 рублей во время распродажи, когда скидка составляет 25% ? 2. Студент получил свой первый гонорар в размере 700 рублей за выполненный перевод. Он решил на все полученные деньги купить букет тюльпанов для своей учительницы английского языка. Какое наибольшее количество тюльпанов сможет купить студент, если удержанный у него налог на доходы составляет 13% гонорара, тюльпаны стоят 60 рублей за штуку и букет должен состоять из нечетного числа цветов? 3. Билет на автобус стоит 15 рублей. Какое максимальное число билетов можно будет купить на 100 рублей после повышения цены билета на 20%?
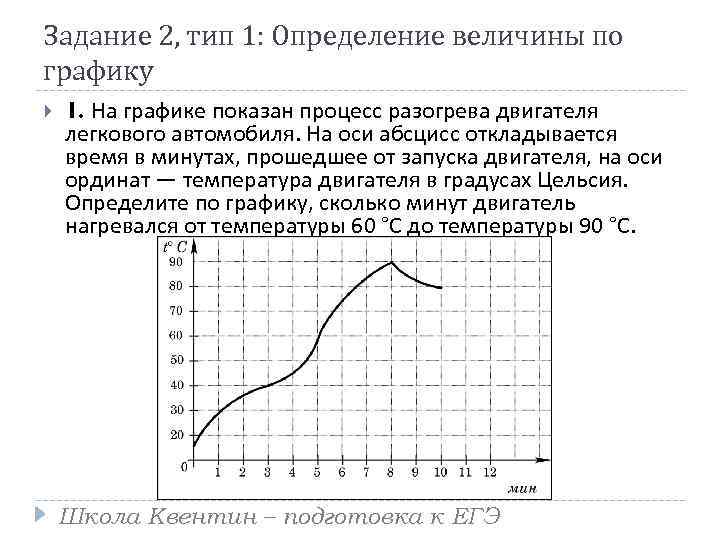 Задание 2, тип 1: Определение величины по графику 1. На графике показан процесс разогрева двигателя легкового автомобиля. На оси абсцисс откладывается время в минутах, прошедшее от запуска двигателя, на оси ординат — температура двигателя в градусах Цельсия. Определите по графику, сколько минут двигатель нагревался от температуры 60 °C до температуры 90 °C. Школа Квентин – подготовка к ЕГЭ
Задание 2, тип 1: Определение величины по графику 1. На графике показан процесс разогрева двигателя легкового автомобиля. На оси абсцисс откладывается время в минутах, прошедшее от запуска двигателя, на оси ординат — температура двигателя в градусах Цельсия. Определите по графику, сколько минут двигатель нагревался от температуры 60 °C до температуры 90 °C. Школа Квентин – подготовка к ЕГЭ
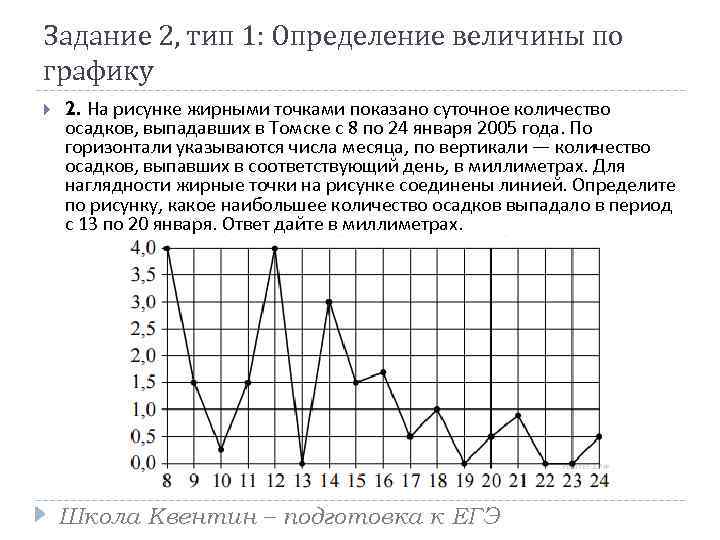 Задание 2, тип 1: Определение величины по графику 2. На рисунке жирными точками показано суточное количество осадков, выпадавших в Томске с 8 по 24 января 2005 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какое наибольшее количество осадков выпадало в период с 13 по 20 января. Ответ дайте в миллиметрах. Школа Квентин – подготовка к ЕГЭ
Задание 2, тип 1: Определение величины по графику 2. На рисунке жирными точками показано суточное количество осадков, выпадавших в Томске с 8 по 24 января 2005 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какое наибольшее количество осадков выпадало в период с 13 по 20 января. Ответ дайте в миллиметрах. Школа Квентин – подготовка к ЕГЭ
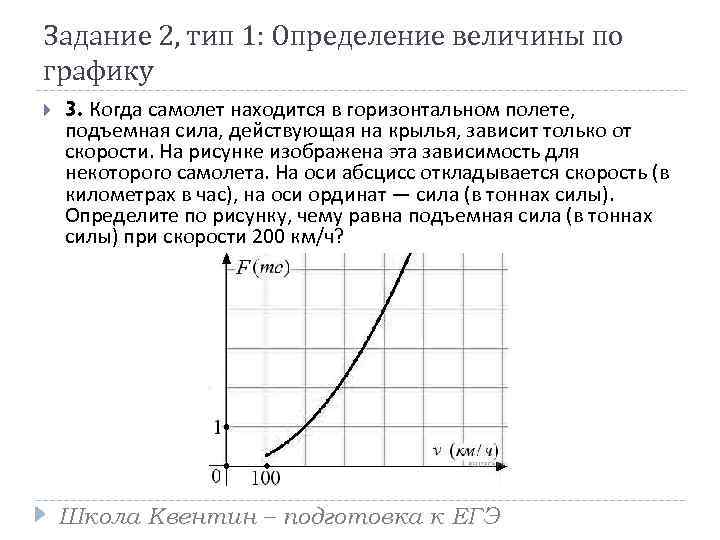 Задание 2, тип 1: Определение величины по графику 3. Когда самолет находится в горизонтальном полете, подъемная сила, действующая на крылья, зависит только от скорости. На рисунке изображена эта зависимость для некоторого самолета. На оси абсцисс откладывается скорость (в километрах в час), на оси ординат — сила (в тоннах силы). Определите по рисунку, чему равна подъемная сила (в тоннах силы) при скорости 200 км/ч? Школа Квентин – подготовка к ЕГЭ
Задание 2, тип 1: Определение величины по графику 3. Когда самолет находится в горизонтальном полете, подъемная сила, действующая на крылья, зависит только от скорости. На рисунке изображена эта зависимость для некоторого самолета. На оси абсцисс откладывается скорость (в километрах в час), на оси ординат — сила (в тоннах силы). Определите по рисунку, чему равна подъемная сила (в тоннах силы) при скорости 200 км/ч? Школа Квентин – подготовка к ЕГЭ
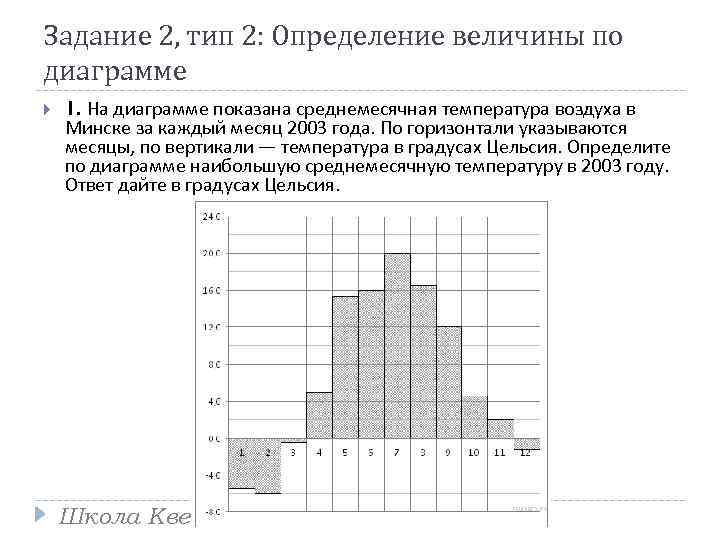 Задание 2, тип 2: Определение величины по диаграмме 1. На диаграмме показана среднемесячная температура воздуха в Минске за каждый месяц 2003 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наибольшую среднемесячную температуру в 2003 году. Ответ дайте в градусах Цельсия. Школа Квентин – подготовка к ЕГЭ
Задание 2, тип 2: Определение величины по диаграмме 1. На диаграмме показана среднемесячная температура воздуха в Минске за каждый месяц 2003 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наибольшую среднемесячную температуру в 2003 году. Ответ дайте в градусах Цельсия. Школа Квентин – подготовка к ЕГЭ
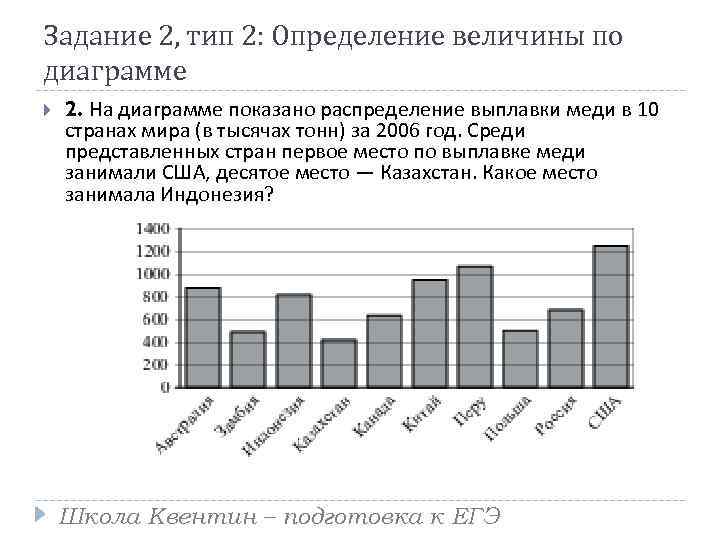 Задание 2, тип 2: Определение величины по диаграмме 2. На диаграмме показано распределение выплавки меди в 10 странах мира (в тысячах тонн) за 2006 год. Среди представленных стран первое место по выплавке меди занимали США, десятое место — Казахстан. Какое место занимала Индонезия? Школа Квентин – подготовка к ЕГЭ
Задание 2, тип 2: Определение величины по диаграмме 2. На диаграмме показано распределение выплавки меди в 10 странах мира (в тысячах тонн) за 2006 год. Среди представленных стран первое место по выплавке меди занимали США, десятое место — Казахстан. Какое место занимала Индонезия? Школа Квентин – подготовка к ЕГЭ
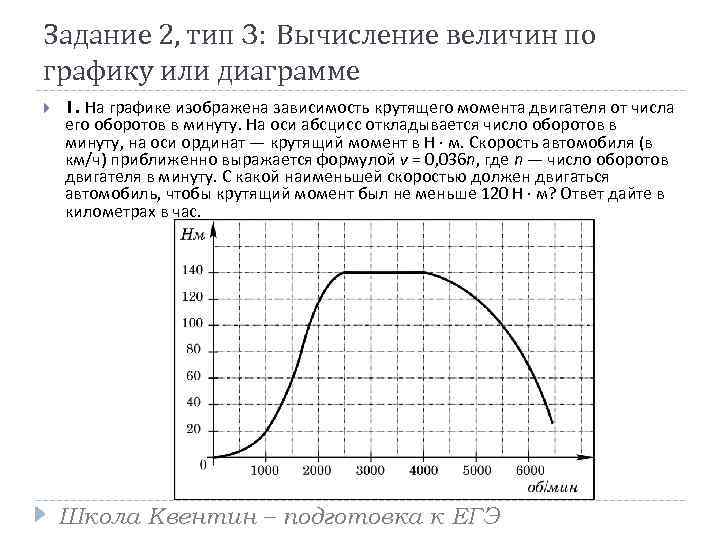 Задание 2, тип 3: Вычисление величин по графику или диаграмме 1. На графике изображена зависимость крутящего момента двигателя от числа его оборотов в минуту. На оси абсцисс откладывается число оборотов в минуту, на оси ординат — крутящий момент в Н · м. Скорость автомобиля (в км/ч) приближенно выражается формулой v = 0, 036 n, где n — число оборотов двигателя в минуту. С какой наименьшей скоростью должен двигаться автомобиль, чтобы крутящий момент был не меньше 120 Н · м? Ответ дайте в километрах в час. Школа Квентин – подготовка к ЕГЭ
Задание 2, тип 3: Вычисление величин по графику или диаграмме 1. На графике изображена зависимость крутящего момента двигателя от числа его оборотов в минуту. На оси абсцисс откладывается число оборотов в минуту, на оси ординат — крутящий момент в Н · м. Скорость автомобиля (в км/ч) приближенно выражается формулой v = 0, 036 n, где n — число оборотов двигателя в минуту. С какой наименьшей скоростью должен двигаться автомобиль, чтобы крутящий момент был не меньше 120 Н · м? Ответ дайте в километрах в час. Школа Квентин – подготовка к ЕГЭ
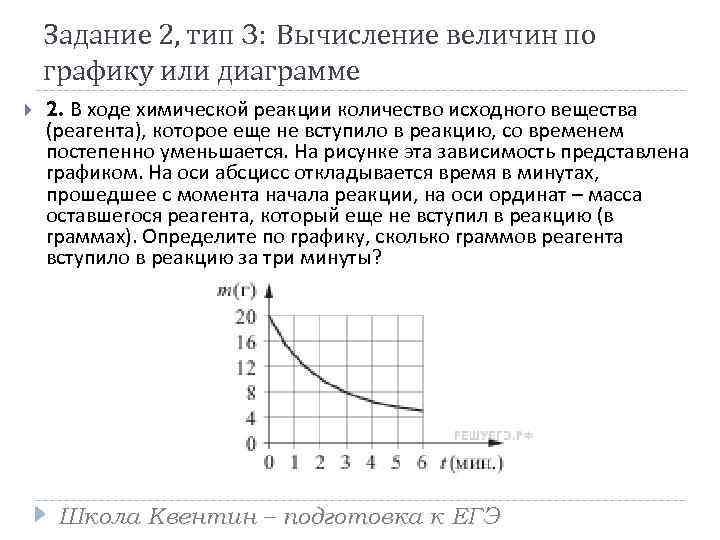 Задание 2, тип 3: Вычисление величин по графику или диаграмме 2. В ходе химической реакции количество исходного вещества (реагента), которое еще не вступило в реакцию, со временем постепенно уменьшается. На рисунке эта зависимость представлена графиком. На оси абсцисс откладывается время в минутах, прошедшее с момента начала реакции, на оси ординат – масса оставшегося реагента, который еще не вступил в реакцию (в граммах). Определите по графику, сколько граммов реагента вступило в реакцию за три минуты? Школа Квентин – подготовка к ЕГЭ
Задание 2, тип 3: Вычисление величин по графику или диаграмме 2. В ходе химической реакции количество исходного вещества (реагента), которое еще не вступило в реакцию, со временем постепенно уменьшается. На рисунке эта зависимость представлена графиком. На оси абсцисс откладывается время в минутах, прошедшее с момента начала реакции, на оси ординат – масса оставшегося реагента, который еще не вступил в реакцию (в граммах). Определите по графику, сколько граммов реагента вступило в реакцию за три минуты? Школа Квентин – подготовка к ЕГЭ
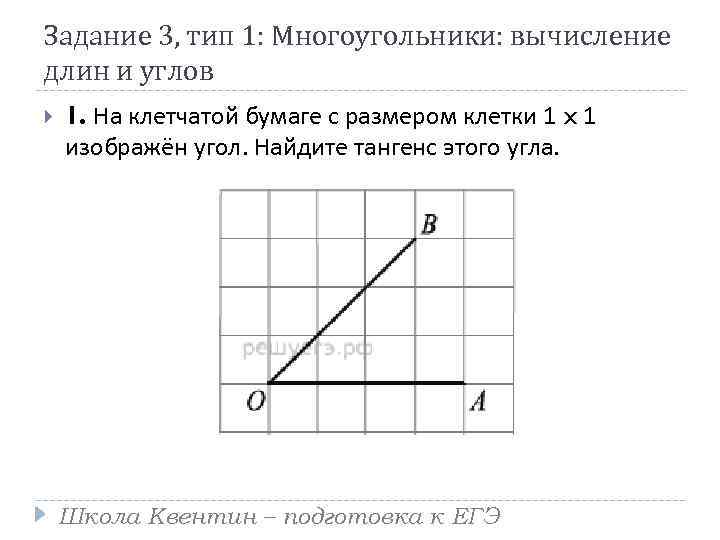 Задание 3, тип 1: Многоугольники: вычисление длин и углов 1. На клетчатой бумаге с размером клетки 1 x 1 изображён угол. Найдите тангенс этого угла. Школа Квентин – подготовка к ЕГЭ
Задание 3, тип 1: Многоугольники: вычисление длин и углов 1. На клетчатой бумаге с размером клетки 1 x 1 изображён угол. Найдите тангенс этого угла. Школа Квентин – подготовка к ЕГЭ
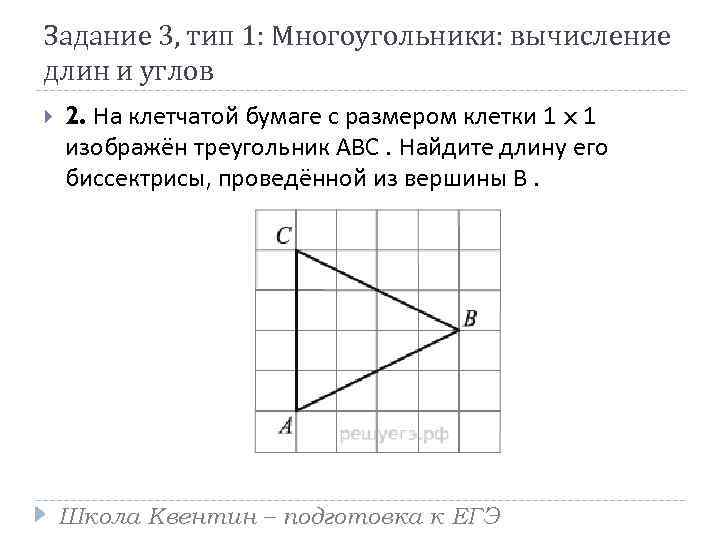 Задание 3, тип 1: Многоугольники: вычисление длин и углов 2. На клетчатой бумаге с размером клетки 1 x 1 изображён треугольник ABC. Найдите длину его биссектрисы, проведённой из вершины B. Школа Квентин – подготовка к ЕГЭ
Задание 3, тип 1: Многоугольники: вычисление длин и углов 2. На клетчатой бумаге с размером клетки 1 x 1 изображён треугольник ABC. Найдите длину его биссектрисы, проведённой из вершины B. Школа Квентин – подготовка к ЕГЭ
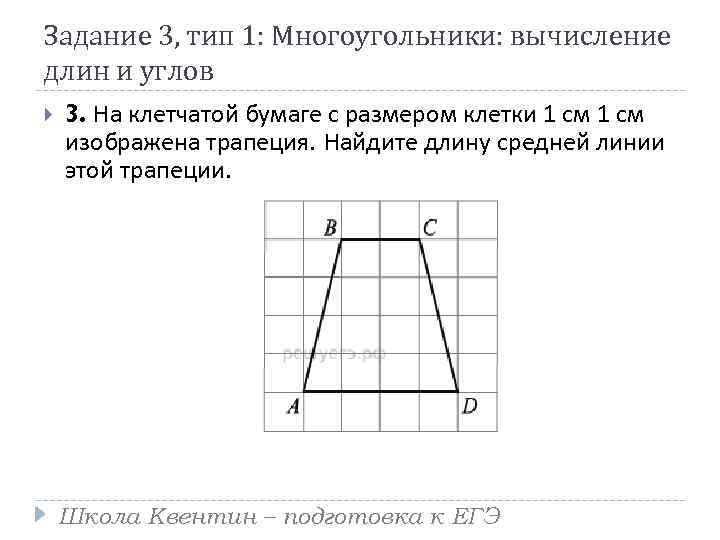 Задание 3, тип 1: Многоугольники: вычисление длин и углов 3. На клетчатой бумаге с размером клетки 1 см изображена трапеция. Найдите длину средней линии этой трапеции. Школа Квентин – подготовка к ЕГЭ
Задание 3, тип 1: Многоугольники: вычисление длин и углов 3. На клетчатой бумаге с размером клетки 1 см изображена трапеция. Найдите длину средней линии этой трапеции. Школа Квентин – подготовка к ЕГЭ
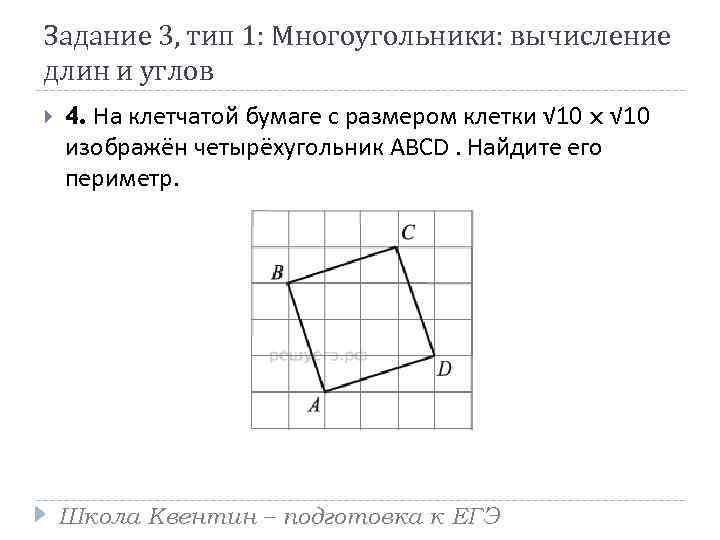 Задание 3, тип 1: Многоугольники: вычисление длин и углов 4. На клетчатой бумаге с размером клетки √ 10 x √ 10 изображён четырёхугольник ABCD. Найдите его периметр. Школа Квентин – подготовка к ЕГЭ
Задание 3, тип 1: Многоугольники: вычисление длин и углов 4. На клетчатой бумаге с размером клетки √ 10 x √ 10 изображён четырёхугольник ABCD. Найдите его периметр. Школа Квентин – подготовка к ЕГЭ
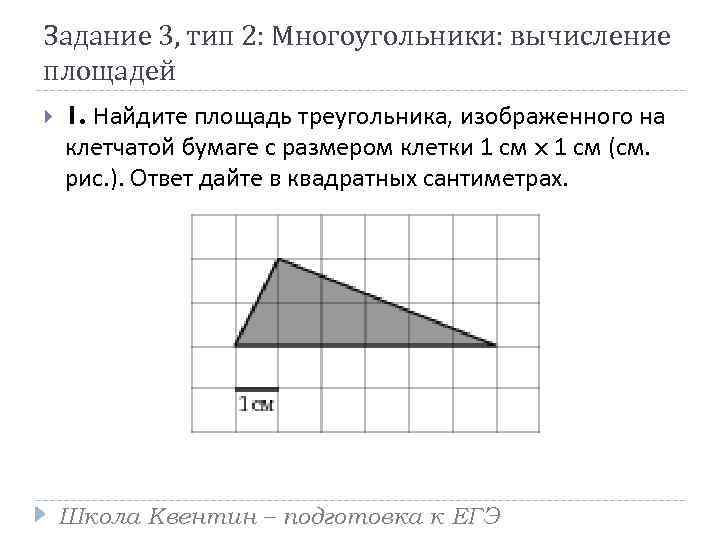 Задание 3, тип 2: Многоугольники: вычисление площадей 1. Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см x 1 см (см. рис. ). Ответ дайте в квадратных сантиметрах. Школа Квентин – подготовка к ЕГЭ
Задание 3, тип 2: Многоугольники: вычисление площадей 1. Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см x 1 см (см. рис. ). Ответ дайте в квадратных сантиметрах. Школа Квентин – подготовка к ЕГЭ
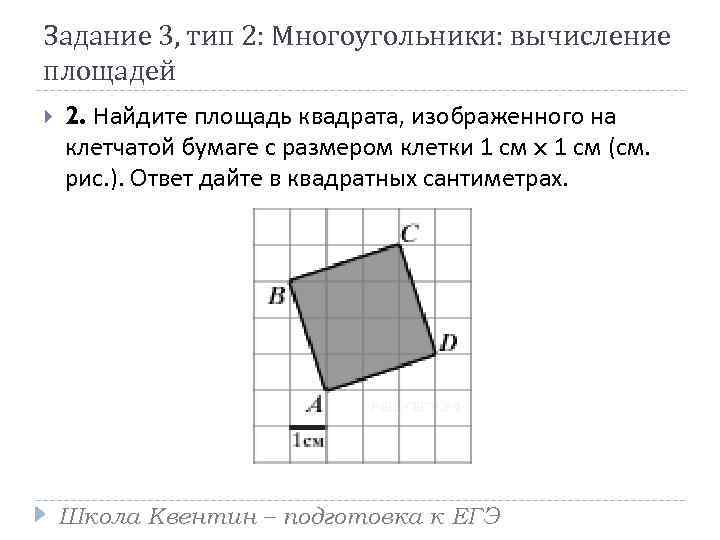 Задание 3, тип 2: Многоугольники: вычисление площадей 2. Найдите площадь квадрата, изображенного на клетчатой бумаге с размером клетки 1 см x 1 см (см. рис. ). Ответ дайте в квадратных сантиметрах. Школа Квентин – подготовка к ЕГЭ
Задание 3, тип 2: Многоугольники: вычисление площадей 2. Найдите площадь квадрата, изображенного на клетчатой бумаге с размером клетки 1 см x 1 см (см. рис. ). Ответ дайте в квадратных сантиметрах. Школа Квентин – подготовка к ЕГЭ
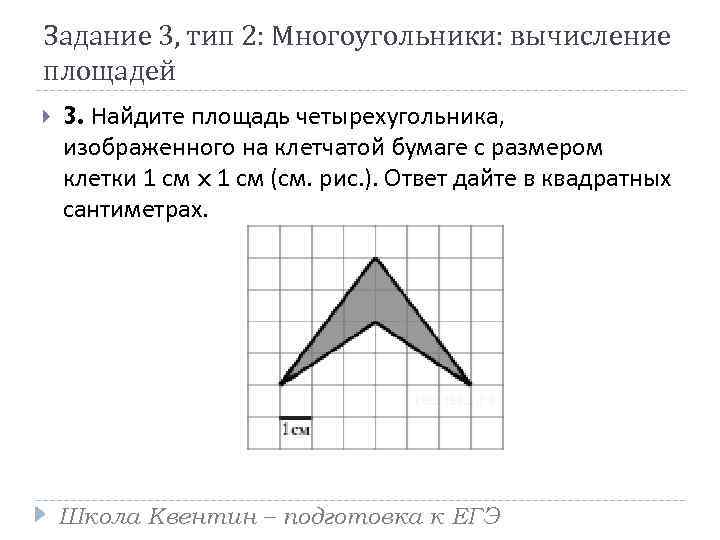 Задание 3, тип 2: Многоугольники: вычисление площадей 3. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см x 1 см (см. рис. ). Ответ дайте в квадратных сантиметрах. Школа Квентин – подготовка к ЕГЭ
Задание 3, тип 2: Многоугольники: вычисление площадей 3. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см x 1 см (см. рис. ). Ответ дайте в квадратных сантиметрах. Школа Квентин – подготовка к ЕГЭ
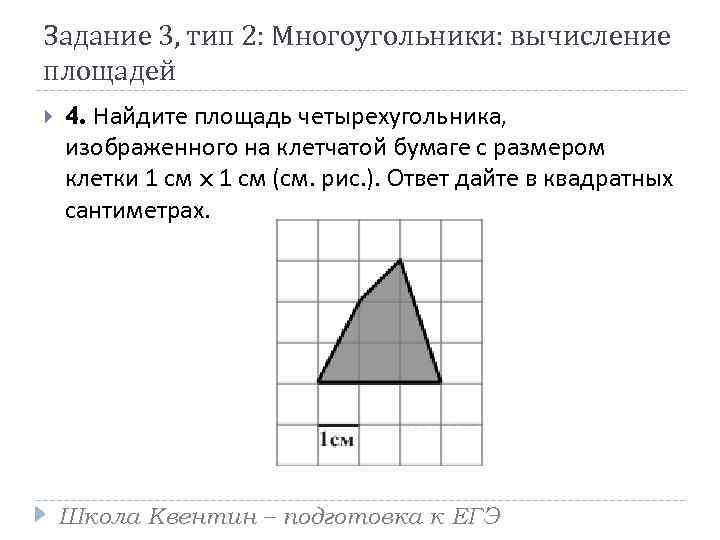 Задание 3, тип 2: Многоугольники: вычисление площадей 4. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см x 1 см (см. рис. ). Ответ дайте в квадратных сантиметрах. Школа Квентин – подготовка к ЕГЭ
Задание 3, тип 2: Многоугольники: вычисление площадей 4. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см x 1 см (см. рис. ). Ответ дайте в квадратных сантиметрах. Школа Квентин – подготовка к ЕГЭ
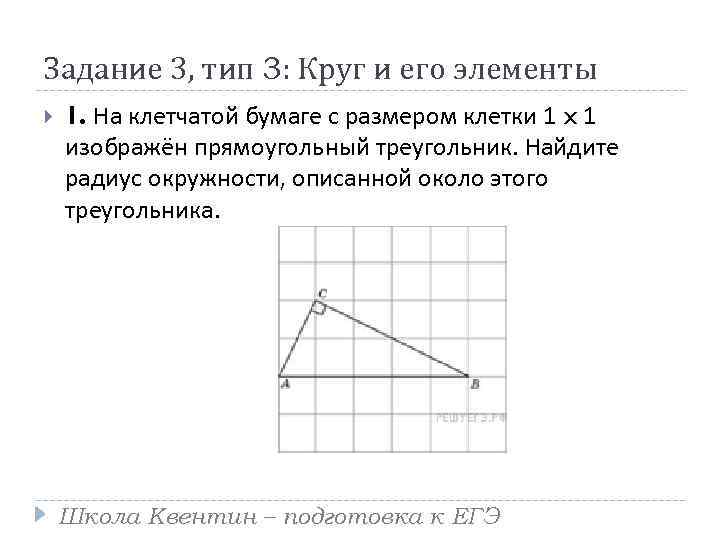 Задание 3, тип 3: Круг и его элементы 1. На клетчатой бумаге с размером клетки 1 x 1 изображён прямоугольный треугольник. Найдите радиус окружности, описанной около этого треугольника. Школа Квентин – подготовка к ЕГЭ
Задание 3, тип 3: Круг и его элементы 1. На клетчатой бумаге с размером клетки 1 x 1 изображён прямоугольный треугольник. Найдите радиус окружности, описанной около этого треугольника. Школа Квентин – подготовка к ЕГЭ
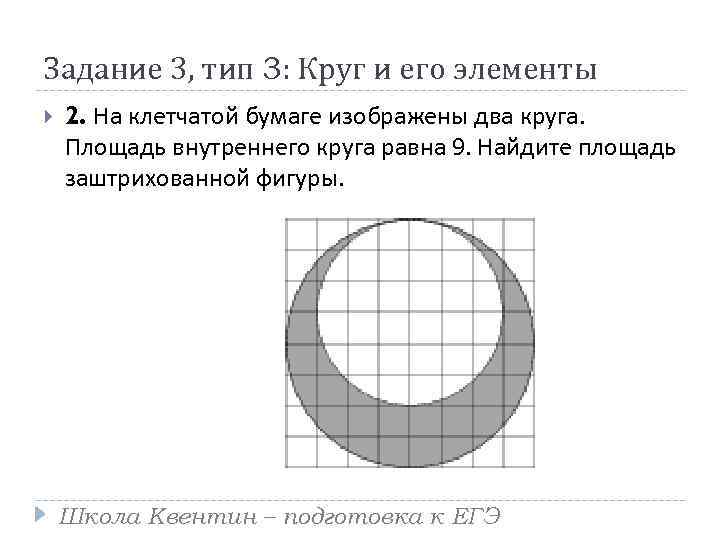 Задание 3, тип 3: Круг и его элементы 2. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 9. Найдите площадь заштрихованной фигуры. Школа Квентин – подготовка к ЕГЭ
Задание 3, тип 3: Круг и его элементы 2. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 9. Найдите площадь заштрихованной фигуры. Школа Квентин – подготовка к ЕГЭ
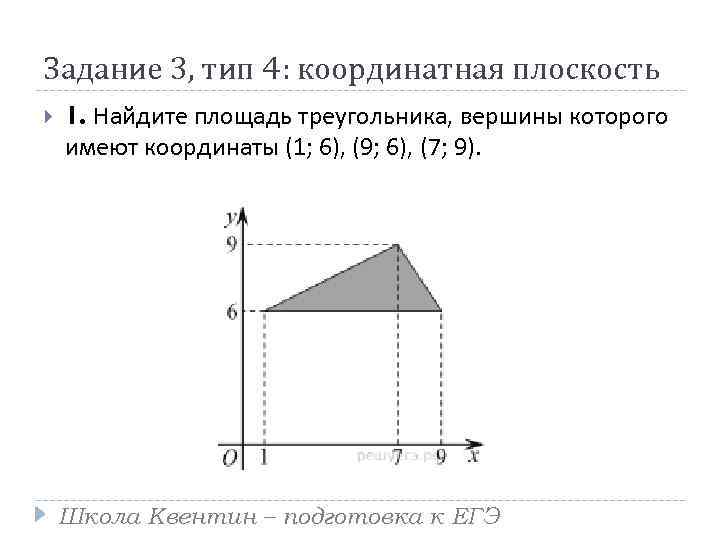 Задание 3, тип 4: координатная плоскость 1. Найдите площадь треугольника, вершины которого имеют координаты (1; 6), (9; 6), (7; 9). Школа Квентин – подготовка к ЕГЭ
Задание 3, тип 4: координатная плоскость 1. Найдите площадь треугольника, вершины которого имеют координаты (1; 6), (9; 6), (7; 9). Школа Квентин – подготовка к ЕГЭ
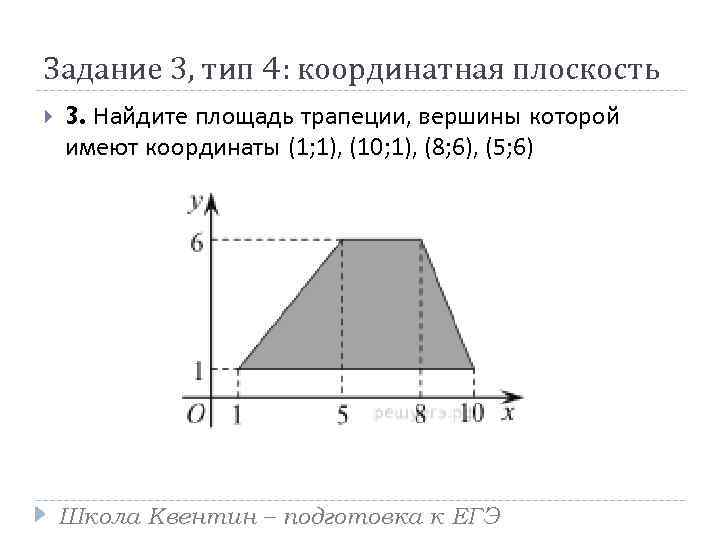 Задание 3, тип 4: координатная плоскость 3. Найдите площадь трапеции, вершины которой имеют координаты (1; 1), (10; 1), (8; 6), (5; 6) Школа Квентин – подготовка к ЕГЭ
Задание 3, тип 4: координатная плоскость 3. Найдите площадь трапеции, вершины которой имеют координаты (1; 1), (10; 1), (8; 6), (5; 6) Школа Квентин – подготовка к ЕГЭ
 Задание 4, тип 1: классическое определение вероятности 1. На тарелке 16 пирожков: 7 с рыбой, 5 с вареньем и 4 с вишней. Юля наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней. 2. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых. 3. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.
Задание 4, тип 1: классическое определение вероятности 1. На тарелке 16 пирожков: 7 с рыбой, 5 с вареньем и 4 с вишней. Юля наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней. 2. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых. 3. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.
 Задание 4, тип 1: классическое определение вероятности 4. Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали идти. Найдите вероятность того, что часовая стрелка остановилась, достигнув отметки 10, но не дойдя до отметки 1. 5. За круглый стол на 17 стульев в случайном порядке рассаживаются 15 мальчиков и 2 девочки. Найдите вероятность того, что девочки будут сидеть рядом. 6. За круглый стол на 201 стул в случайном порядке рассаживаются 199 мальчиков и 2 девочки. Найдите вероятность того, что между девочками будет сидеть один мальчик. 7. При производстве в среднем на каждые 2982 исправных насоса приходится 18 неисправных. Найдите вероятность того, что случайно выбранный насос окажется неисправным.
Задание 4, тип 1: классическое определение вероятности 4. Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали идти. Найдите вероятность того, что часовая стрелка остановилась, достигнув отметки 10, но не дойдя до отметки 1. 5. За круглый стол на 17 стульев в случайном порядке рассаживаются 15 мальчиков и 2 девочки. Найдите вероятность того, что девочки будут сидеть рядом. 6. За круглый стол на 201 стул в случайном порядке рассаживаются 199 мальчиков и 2 девочки. Найдите вероятность того, что между девочками будет сидеть один мальчик. 7. При производстве в среднем на каждые 2982 исправных насоса приходится 18 неисправных. Найдите вероятность того, что случайно выбранный насос окажется неисправным.
 Задание 4, тип 2: Теоремы о вероятностях событий 1. Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 18 пассажиров, равна 0, 82. Вероятность того, что окажется меньше 10 пассажиров, равна 0, 51. Найдите вероятность того, что число пассажиров будет от 10 до 17. 2. У Пети два маркера. Вероятность использования одного маркера в течение недели равна 0, 4. Найдите вероятность того, что в течение недели хотя бы один маркер не будет использован 3. Вероятность того, что в случайный момент времени температура тела здорового человека окажется ниже чем 36, 8 °С, равна 0, 81. Найдите вероятность того, что в случайный момент времени у здорового человека температура окажется 36, 8 °С или выше.
Задание 4, тип 2: Теоремы о вероятностях событий 1. Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 18 пассажиров, равна 0, 82. Вероятность того, что окажется меньше 10 пассажиров, равна 0, 51. Найдите вероятность того, что число пассажиров будет от 10 до 17. 2. У Пети два маркера. Вероятность использования одного маркера в течение недели равна 0, 4. Найдите вероятность того, что в течение недели хотя бы один маркер не будет использован 3. Вероятность того, что в случайный момент времени температура тела здорового человека окажется ниже чем 36, 8 °С, равна 0, 81. Найдите вероятность того, что в случайный момент времени у здорового человека температура окажется 36, 8 °С или выше.
 Задание 4, тип 2: Теоремы о вероятностях событий 4. При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0, 4, а при каждом последующем — 0, 6. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0, 98?
Задание 4, тип 2: Теоремы о вероятностях событий 4. При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0, 4, а при каждом последующем — 0, 6. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0, 98?
 Задание 5, тип 1: Линейные, квадратные, кубические уравнения 1. Решите уравнение 2. Найдите корень уравнения. Если уравнение имеет более одного корня, в ответе запишите меньший из корней. 3. Найдите корень уравнения 4. Решите уравнение
Задание 5, тип 1: Линейные, квадратные, кубические уравнения 1. Решите уравнение 2. Найдите корень уравнения. Если уравнение имеет более одного корня, в ответе запишите меньший из корней. 3. Найдите корень уравнения 4. Решите уравнение
 Задание 5, тип 2: Рациональные уравнения 1. Найдите корень уравнения: 2. Найдите корень уравнения. Если уравнение имеет более одного корня, в ответе запишите больший из корней.
Задание 5, тип 2: Рациональные уравнения 1. Найдите корень уравнения: 2. Найдите корень уравнения. Если уравнение имеет более одного корня, в ответе запишите больший из корней.
 Задание 5, тип 2: Рациональные уравнения 3. Решите уравнение. Если уравнение имеет более одного корня, в ответе запишите больший из корней. 4. Найдите корень уравнения
Задание 5, тип 2: Рациональные уравнения 3. Решите уравнение. Если уравнение имеет более одного корня, в ответе запишите больший из корней. 4. Найдите корень уравнения
 Задание 5, тип 3: Иррациональные уравнения 1. Найдите корень уравнения 2. Найдите корень уравнения 3. Найдите корень уравнения 4. Решите уравнение:
Задание 5, тип 3: Иррациональные уравнения 1. Найдите корень уравнения 2. Найдите корень уравнения 3. Найдите корень уравнения 4. Решите уравнение:
 Задание 5, тип 4: Показательные уравнения 1. Найдите корень уравнения 2. Найдите корень уравнения 3. Найдите решение уравнения: 4. Найдите корень уравнения
Задание 5, тип 4: Показательные уравнения 1. Найдите корень уравнения 2. Найдите корень уравнения 3. Найдите решение уравнения: 4. Найдите корень уравнения
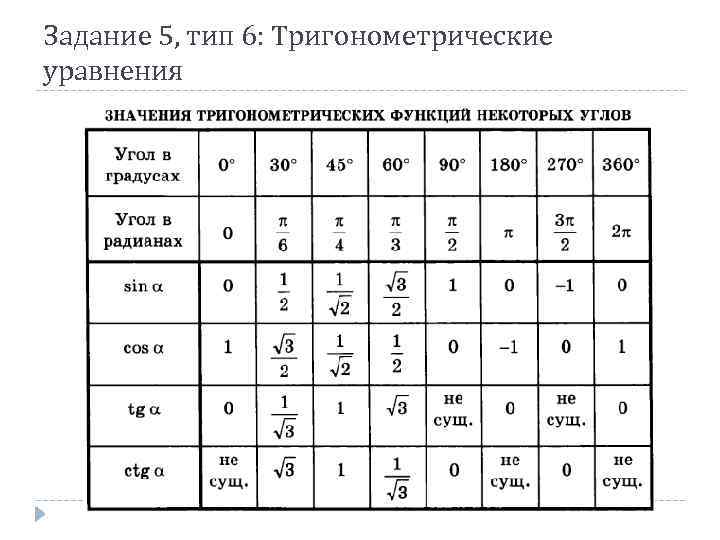 Задание 5, тип 6: Тригонометрические уравнения
Задание 5, тип 6: Тригонометрические уравнения
 Задание 5, тип 6: Тригонометрические уравнения 1. Решите уравнение. В ответе напишите наибольший отрицательный корень. 2. Решите уравнение. В ответе напишите наименьший положительный корень.
Задание 5, тип 6: Тригонометрические уравнения 1. Решите уравнение. В ответе напишите наибольший отрицательный корень. 2. Решите уравнение. В ответе напишите наименьший положительный корень.
 Задание 6, тип 1: Решение прямоугольного треугольника 1. В треугольнике ABC угол C равен 90°, AC=4, 8, sin A = 7/25. Найдите AB. 2. В треугольнике ABC угол C равен 90°, AC = 24, BC = 7. Найдите sin A 3. В треугольнике ABC угол C равен 90°, CH — высота, BC = 8, sin A = 0. 5. Найдите BH. 4. Острые углы прямоугольного треугольника равны 24° и 66°. Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.
Задание 6, тип 1: Решение прямоугольного треугольника 1. В треугольнике ABC угол C равен 90°, AC=4, 8, sin A = 7/25. Найдите AB. 2. В треугольнике ABC угол C равен 90°, AC = 24, BC = 7. Найдите sin A 3. В треугольнике ABC угол C равен 90°, CH — высота, BC = 8, sin A = 0. 5. Найдите BH. 4. Острые углы прямоугольного треугольника равны 24° и 66°. Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.
 Тип 2: Решение равнобедренного треугольника 1. В треугольнике ABC AC = BC = 5, sin A =7/25. Найдите АВ. 2. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 30°. Боковая сторона треугольника равна 10. Найдите площадь этого треугольника.
Тип 2: Решение равнобедренного треугольника 1. В треугольнике ABC AC = BC = 5, sin A =7/25. Найдите АВ. 2. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 30°. Боковая сторона треугольника равна 10. Найдите площадь этого треугольника.
 Тип 3: Треугольники общего вида 1. Найдите площадь треугольника, две стороны которого равны 8 и 12, а угол между ними равен 30°. 2. Площадь треугольника ABC равна 4. DE — средняя линия. Найдите площадь треугольника CDE. 3. В треугольнике ABC AD — биссектриса, угол C равен 30°, угол BAD равен 22°. Найдите угол ADB. Ответ дайте в градусах.
Тип 3: Треугольники общего вида 1. Найдите площадь треугольника, две стороны которого равны 8 и 12, а угол между ними равен 30°. 2. Площадь треугольника ABC равна 4. DE — средняя линия. Найдите площадь треугольника CDE. 3. В треугольнике ABC AD — биссектриса, угол C равен 30°, угол BAD равен 22°. Найдите угол ADB. Ответ дайте в градусах.
 Тип 3: Треугольники общего вида 1. В треугольнике ABC угол C равен 58°, AD и BE — биссектрисы, пересекающиеся в точке O. Найдите угол AOB. Ответ дайте в градусах. 2. В треугольнике ABC угол A равен 60°, угол B равен 82°. AD, BE и CF — высоты, пересекающиеся в точке O. Найдите угол AOF. Ответ дайте в градусах.
Тип 3: Треугольники общего вида 1. В треугольнике ABC угол C равен 58°, AD и BE — биссектрисы, пересекающиеся в точке O. Найдите угол AOB. Ответ дайте в градусах. 2. В треугольнике ABC угол A равен 60°, угол B равен 82°. AD, BE и CF — высоты, пересекающиеся в точке O. Найдите угол AOF. Ответ дайте в градусах.
 Тип 4: Параллелограммы 1. Найдите площадь квадрата, если его диагональ равна 1. 2. Площадь прямоугольника равна 18. Найдите его большую сторону, если она на 3 больше меньшей стороны. 3. Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту этого параллелограмма. 4. Площадь ромба равна 18. Одна из его диагоналей равна 12. Найдите другую диагональ. 5. Найдите большую диагональ ромба, сторона которого равна √ 3 , а острый угол равен 60°.
Тип 4: Параллелограммы 1. Найдите площадь квадрата, если его диагональ равна 1. 2. Площадь прямоугольника равна 18. Найдите его большую сторону, если она на 3 больше меньшей стороны. 3. Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту этого параллелограмма. 4. Площадь ромба равна 18. Одна из его диагоналей равна 12. Найдите другую диагональ. 5. Найдите большую диагональ ромба, сторона которого равна √ 3 , а острый угол равен 60°.
 Тип 5: Трапеции 1. Основания равнобедренной трапеции равны 51 и 65. Боковые стороны равны 25. Найдите синус острого угла трапеции. 2. Основания равнобедренной трапеции равны 17 и 87. Высота трапеции равна 14. Найдите тангенс острого угла. 3. Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите периметр трапеции.
Тип 5: Трапеции 1. Основания равнобедренной трапеции равны 51 и 65. Боковые стороны равны 25. Найдите синус острого угла трапеции. 2. Основания равнобедренной трапеции равны 17 и 87. Высота трапеции равна 14. Найдите тангенс острого угла. 3. Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите периметр трапеции.
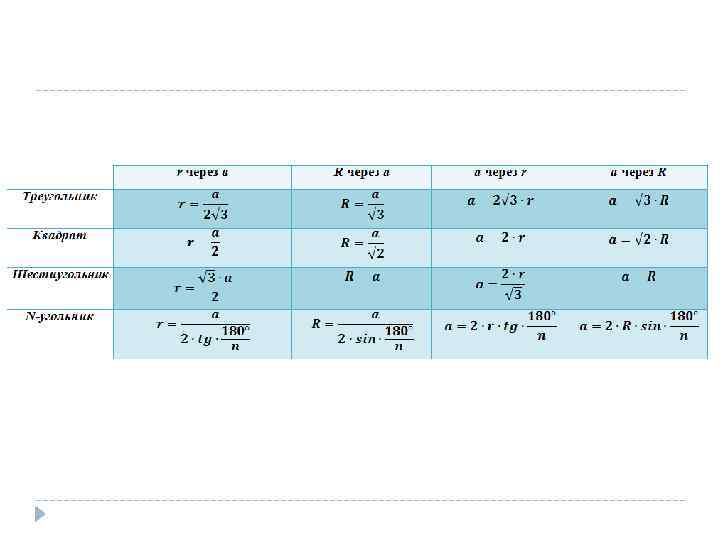
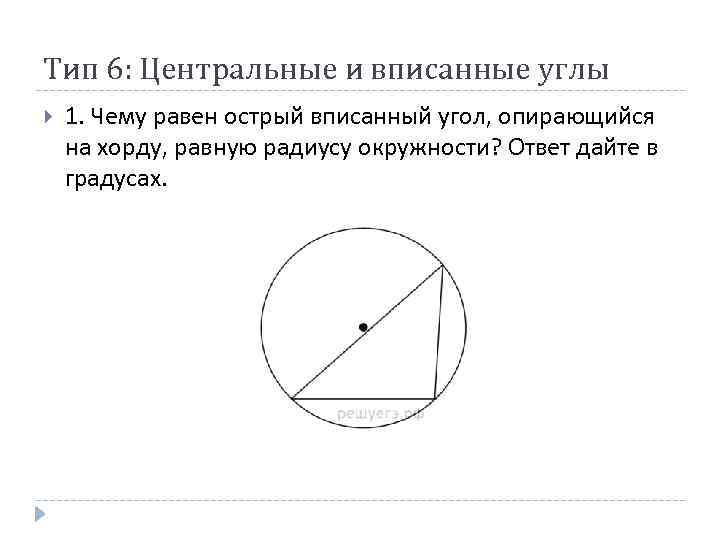 Тип 6: Центральные и вписанные углы 1. Чему равен острый вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах.
Тип 6: Центральные и вписанные углы 1. Чему равен острый вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах.
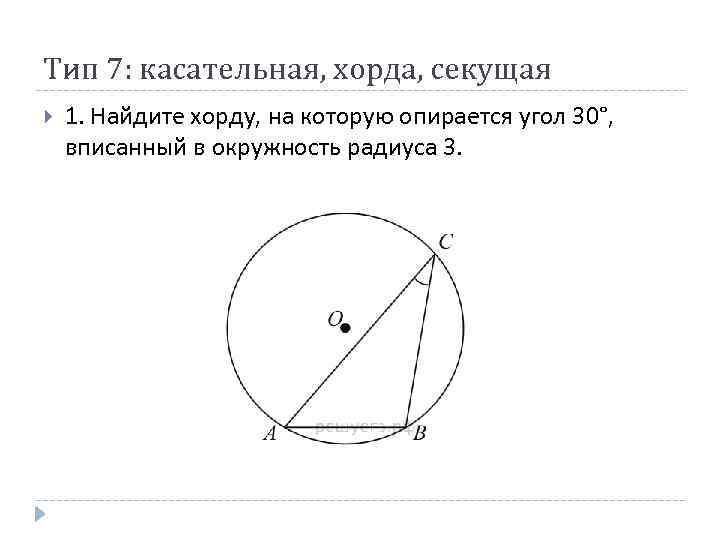 Тип 7: касательная, хорда, секущая 1. Найдите хорду, на которую опирается угол 30°, вписанный в окружность радиуса 3.
Тип 7: касательная, хорда, секущая 1. Найдите хорду, на которую опирается угол 30°, вписанный в окружность радиуса 3.
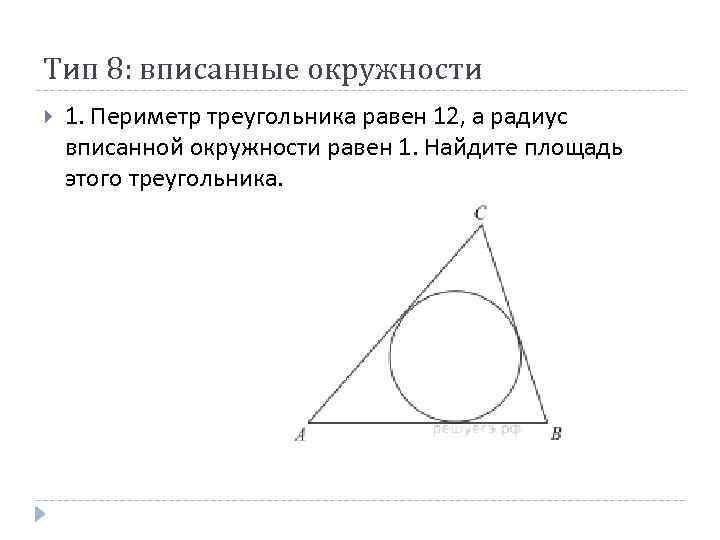 Тип 8: вписанные окружности 1. Периметр треугольника равен 12, а радиус вписанной окружности равен 1. Найдите площадь этого треугольника.
Тип 8: вписанные окружности 1. Периметр треугольника равен 12, а радиус вписанной окружности равен 1. Найдите площадь этого треугольника.
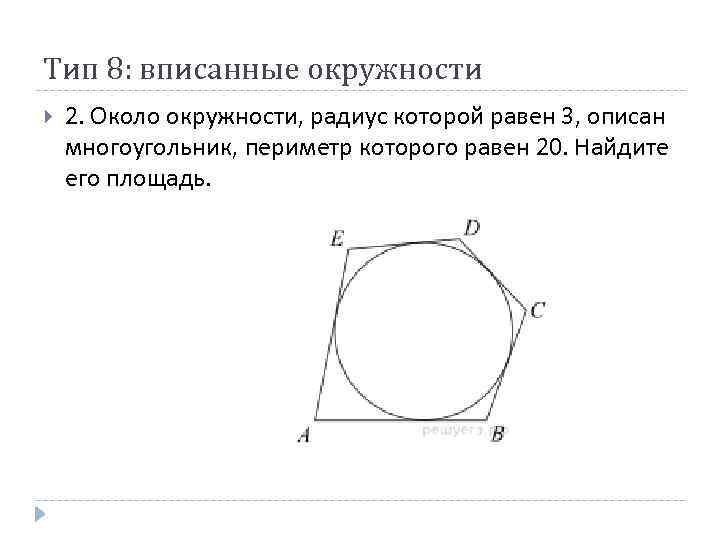 Тип 8: вписанные окружности 2. Около окружности, радиус которой равен 3, описан многоугольник, периметр которого равен 20. Найдите его площадь.
Тип 8: вписанные окружности 2. Около окружности, радиус которой равен 3, описан многоугольник, периметр которого равен 20. Найдите его площадь.
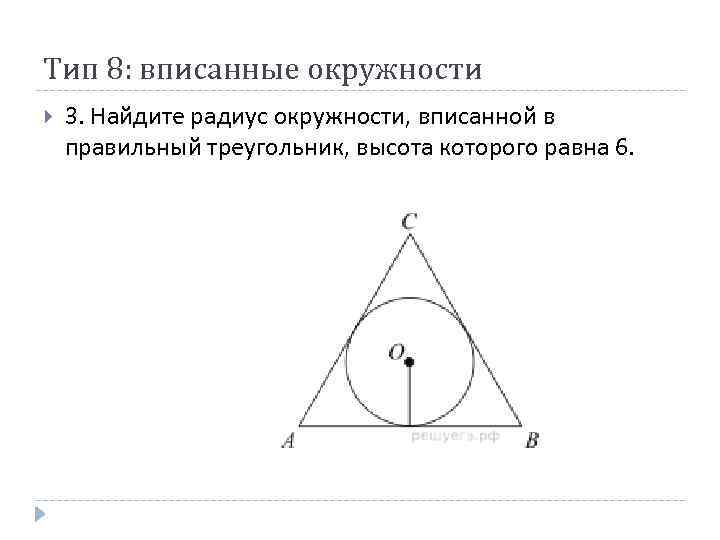 Тип 8: вписанные окружности 3. Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна 6.
Тип 8: вписанные окружности 3. Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна 6.
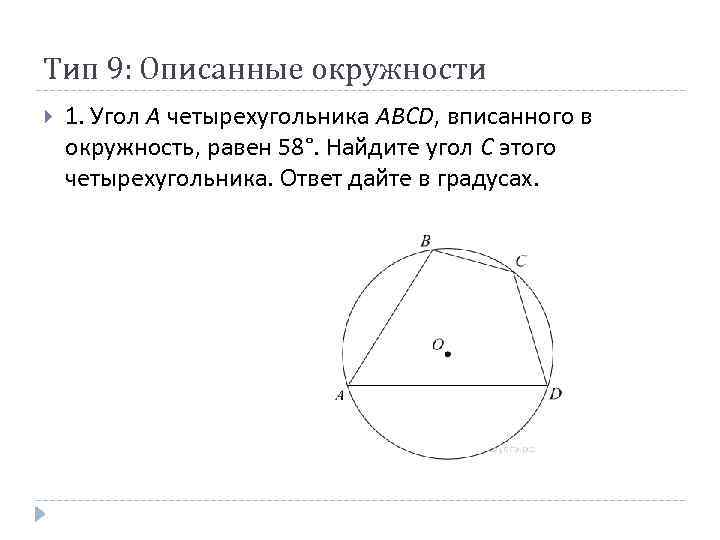 Тип 9: Описанные окружности 1. Угол A четырехугольника ABCD, вписанного в окружность, равен 58°. Найдите угол C этого четырехугольника. Ответ дайте в градусах.
Тип 9: Описанные окружности 1. Угол A четырехугольника ABCD, вписанного в окружность, равен 58°. Найдите угол C этого четырехугольника. Ответ дайте в градусах.
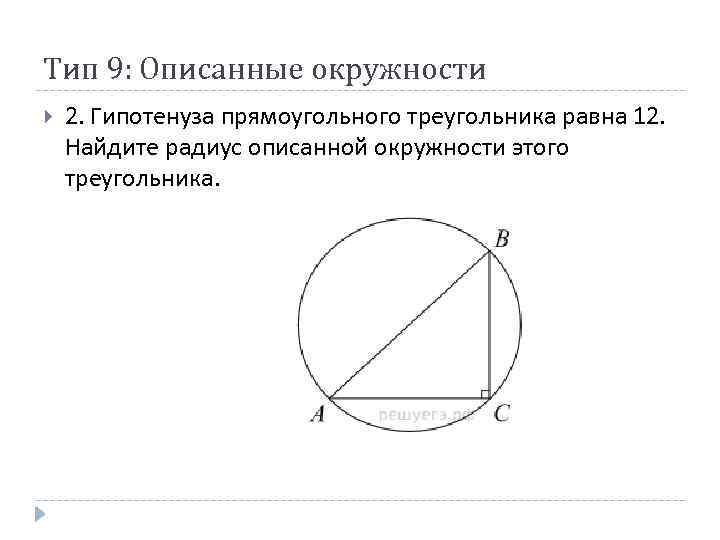 Тип 9: Описанные окружности 2. Гипотенуза прямоугольного треугольника равна 12. Найдите радиус описанной окружности этого треугольника.
Тип 9: Описанные окружности 2. Гипотенуза прямоугольного треугольника равна 12. Найдите радиус описанной окружности этого треугольника.
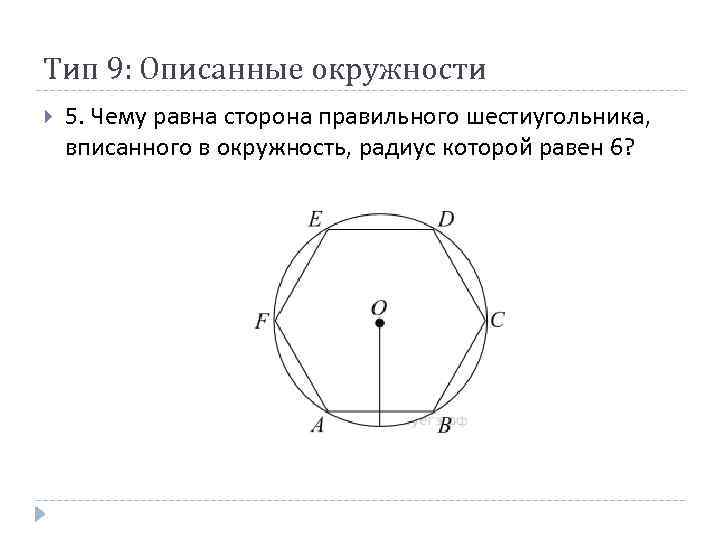 Тип 9: Описанные окружности 5. Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?
Тип 9: Описанные окружности 5. Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?

 Задание 7, тип 1: Физический смысл производной 1. Материальная точка движется прямолинейно по закону x (t) = t 2 – 7 t – 20 где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 5 c.
Задание 7, тип 1: Физический смысл производной 1. Материальная точка движется прямолинейно по закону x (t) = t 2 – 7 t – 20 где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 5 c.
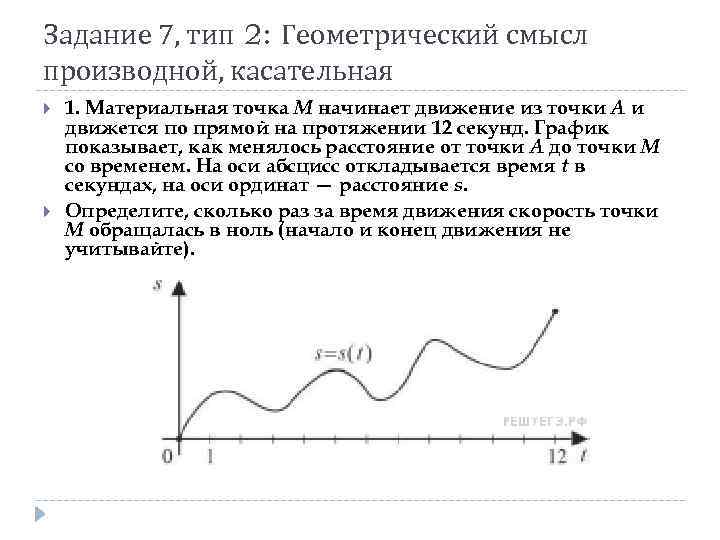 Задание 7, тип 2: Геометрический смысл производной, касательная 1. Материальная точка M начинает движение из точки A и движется по прямой на протяжении 12 секунд. График показывает, как менялось расстояние от точки A до точки M со временем. На оси абсцисс откладывается время t в секундах, на оси ординат — расстояние s. Определите, сколько раз за время движения скорость точки M обращалась в ноль (начало и конец движения не учитывайте).
Задание 7, тип 2: Геометрический смысл производной, касательная 1. Материальная точка M начинает движение из точки A и движется по прямой на протяжении 12 секунд. График показывает, как менялось расстояние от точки A до точки M со временем. На оси абсцисс откладывается время t в секундах, на оси ординат — расстояние s. Определите, сколько раз за время движения скорость точки M обращалась в ноль (начало и конец движения не учитывайте).
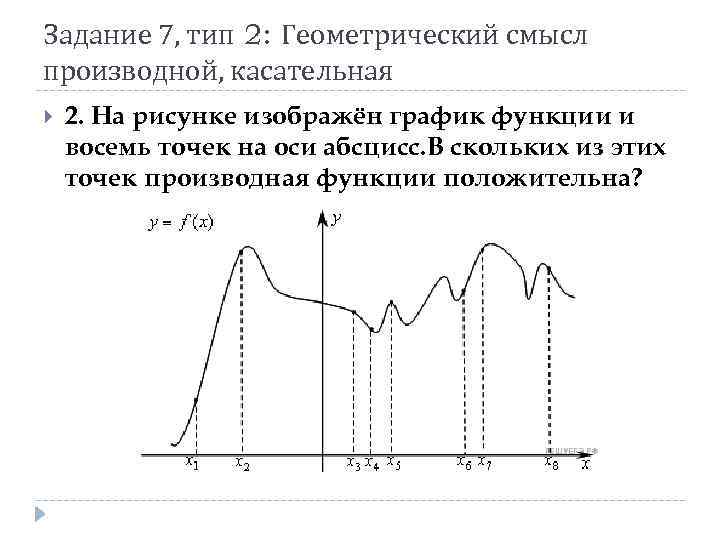 Задание 7, тип 2: Геометрический смысл производной, касательная 2. На рисунке изображён график функции и восемь точек на оси абсцисс. В скольких из этих точек производная функции положительна?
Задание 7, тип 2: Геометрический смысл производной, касательная 2. На рисунке изображён график функции и восемь точек на оси абсцисс. В скольких из этих точек производная функции положительна?
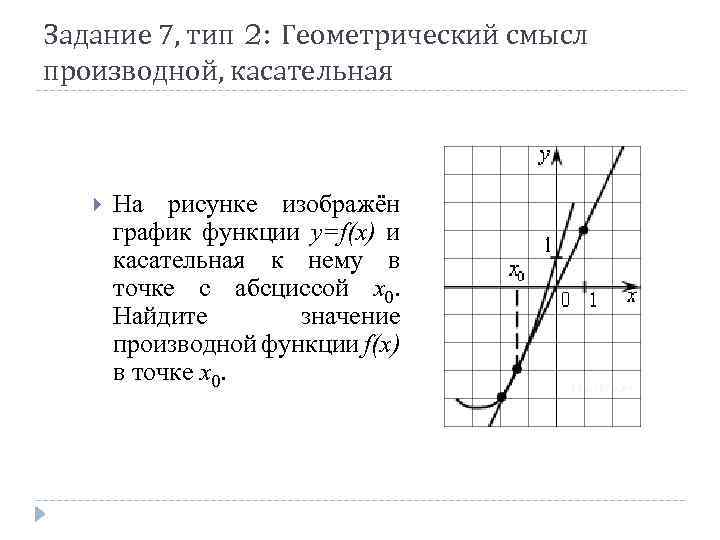 Задание 7, тип 2: Геометрический смысл производной, касательная На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x 0. Найдите значение производной функции f(x) в точке x 0.
Задание 7, тип 2: Геометрический смысл производной, касательная На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x 0. Найдите значение производной функции f(x) в точке x 0.
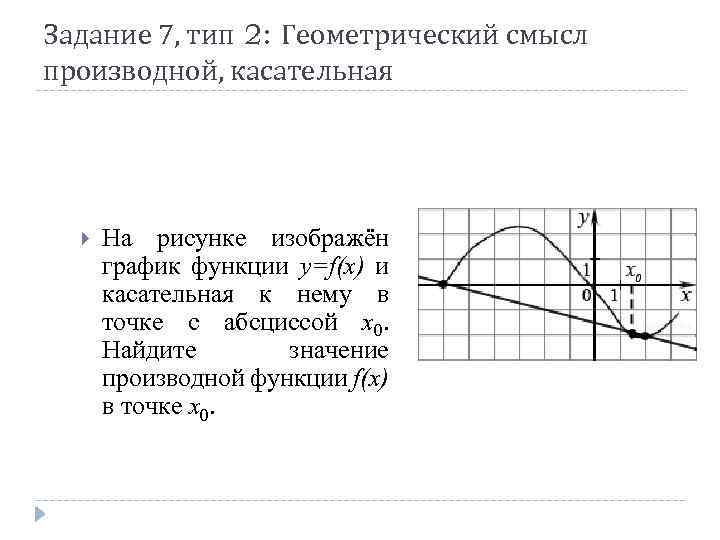 Задание 7, тип 2: Геометрический смысл производной, касательная На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x 0. Найдите значение производной функции f(x) в точке x 0.
Задание 7, тип 2: Геометрический смысл производной, касательная На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x 0. Найдите значение производной функции f(x) в точке x 0.
 Задание 7, тип 2: Геометрический смысл производной, касательная 4. Прямая y=7 x-5 параллельна касательной к графику функции y=x²+6 x-8. Найдите абсциссу точки касания.
Задание 7, тип 2: Геометрический смысл производной, касательная 4. Прямая y=7 x-5 параллельна касательной к графику функции y=x²+6 x-8. Найдите абсциссу точки касания.
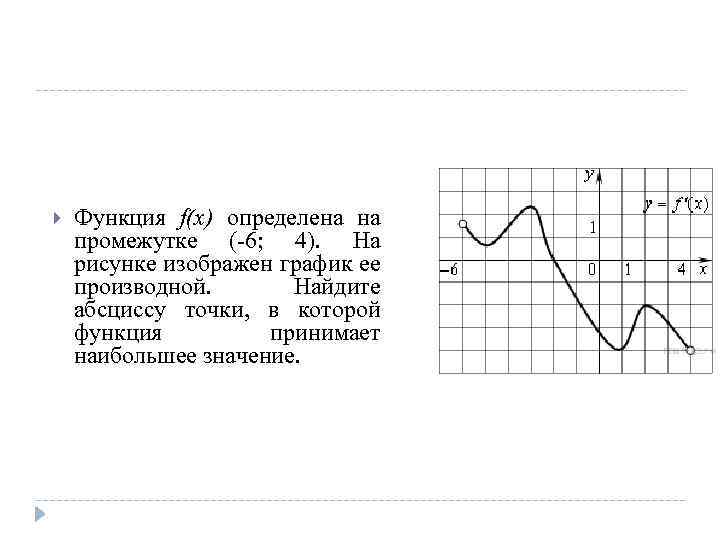 Функция f(x) определена на промежутке (-6; 4). На рисунке изображен график ее производной. Найдите абсциссу точки, в которой функция принимает наибольшее значение.
Функция f(x) определена на промежутке (-6; 4). На рисунке изображен график ее производной. Найдите абсциссу точки, в которой функция принимает наибольшее значение.


