Proceedings of the ASME 2010 International Design Engineering

Proceedings of the ASME 2010 International Design Engineering Technical Conferences &Computers and Information in Engineering Conference IDETC/CIE 2010 August 15 -18, 2010, Montreal, Quebec, Canada, DETC 2010 -28687 EMPLOYING ASSUR TENSEGRITY STRUCTURES FOR SIMULATING A CATERPILLAR LOCOMOTION Omer Orki, Offer Shai, Itay Tehori, Michael Slavutin, Uri Ben-Hanan School of Mechanical Engineering Israel

The outline of the talk: - The main idea. Tensegrity. Assur Graph (Group). Singularity in Assur Graph (main theorem). - Previous application: Adjustable Deployable Tensegrity Structures. - Caterpillar (various types of animals) robot. - Further applications.

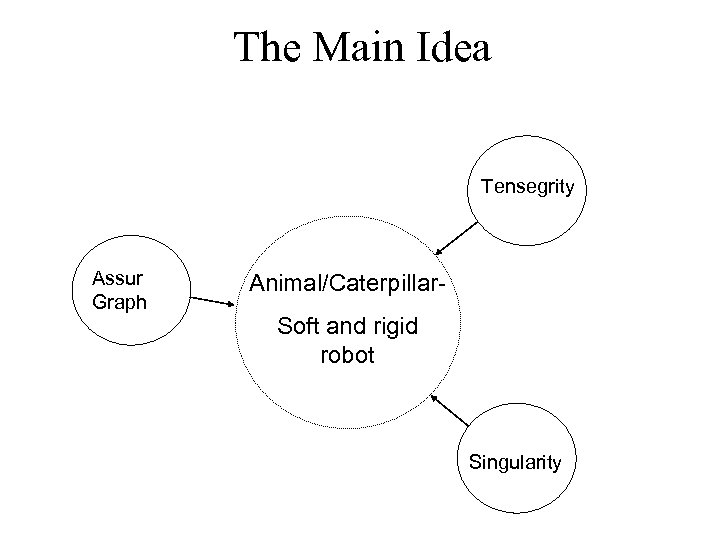The Main Idea Tensegrity Assur Graph Animal/Caterpillar. Soft and rigid robot Singularity

Tensegrity = tension + integrity Consist of: Cables – sustain only tension. Struts - sustain only compression The equilibrium between the two types of forces yields static stability (structural integrity) of the system.

The definition of Assur Graph (Group): Special minimal structures (determinate trusses) with zero mobility from which it is not possible to obtain a simpler substructure of the same mobility. Another definition: Removing any set of joints results in a mobile system.

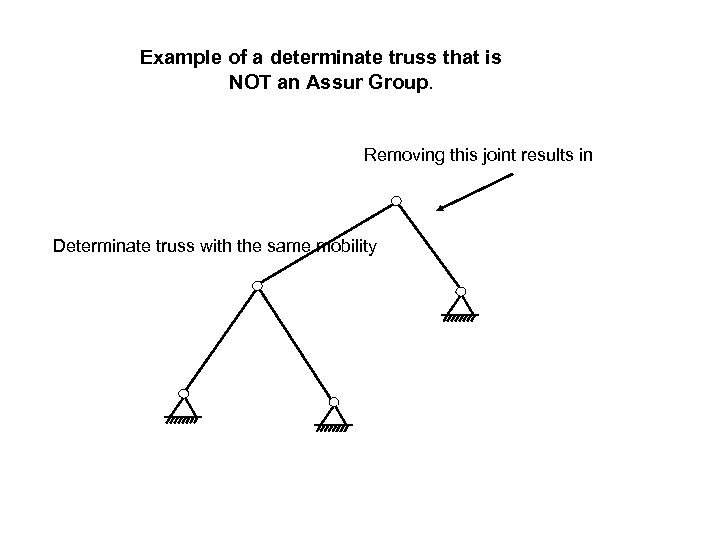Example of a determinate truss that is NOT an Assur Group. Removing this joint results in Determinate truss with the same mobility

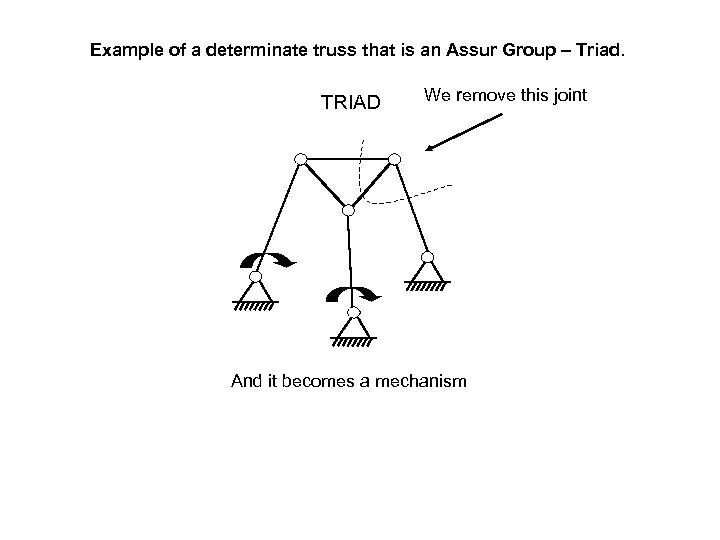Example of a determinate truss that is an Assur Group – Triad. TRIAD We remove this joint And it becomes a mechanism

The MAP of all Assur Graphs in 2 d is complete and sound.

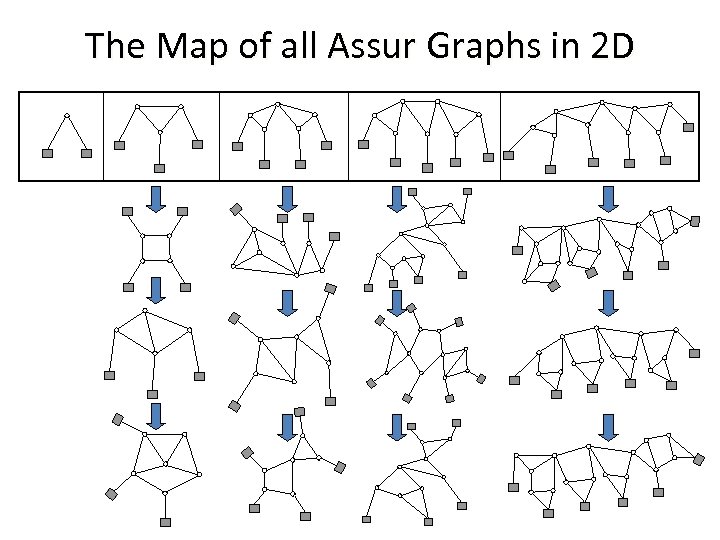The Map of all Assur Graphs in 2 D

Singularity and Mobility Theorem in Assur Graphs

First, let us define: 1. Self-stress. 2. Extended Grubler’s equation.

Self stress Self Stress – A set of forces in the links (internal forces) that satisfy the equilibrium of forces around each joint.

Extended Grubler’s equation = Grubler’s equation + No. self-stresses DOF = 0 + 1 = 1

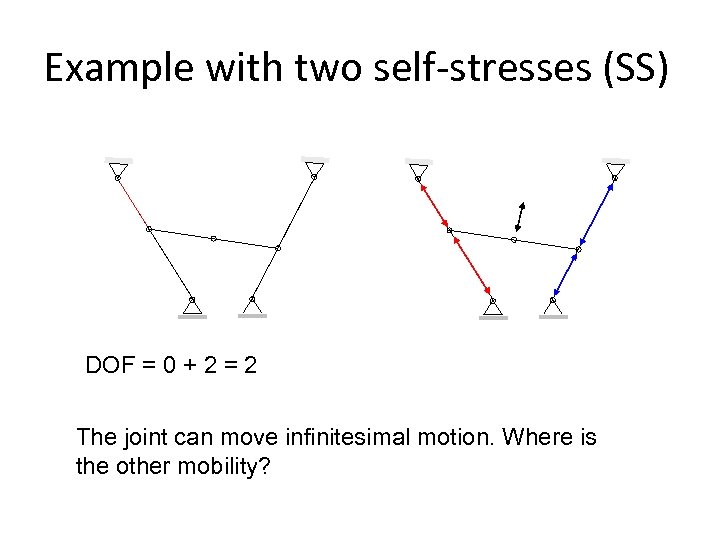Example with two self-stresses (SS) DOF = 0 + 2 = 2 The joint can move infinitesimal motion. Where is the other mobility?

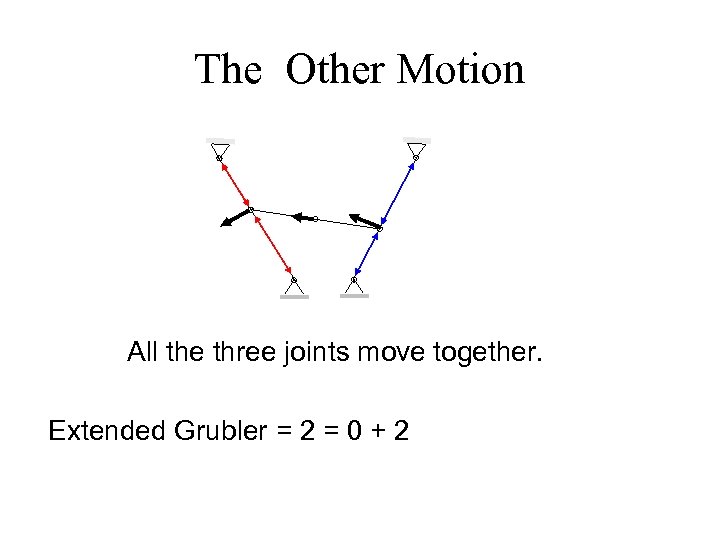The Other Motion All the three joints move together. Extended Grubler = 2 = 0 + 2

Special Singularity and Mobility properties of Assur Graphs: G is an Assur Graph IFF there exists a configuration in which there is a unique selfstress in all the links and all the joints have an infinitesimal motion with 1 DOF. Servatius B. , Shai O. and Whiteley W. , "Combinatorial Characterization of the Assur Graphs from Engineering", European Journal of Combinatorics, Vol. 31, No. 4, May, pp. 1091 -1104, 2010. Servatius B. , Shai O. and Whiteley W. , "Geometric Properties of Assur Graphs", European Journal of Combinatorics, Vol. 31, No. 4, May, pp. 1105 -1120, 2010.

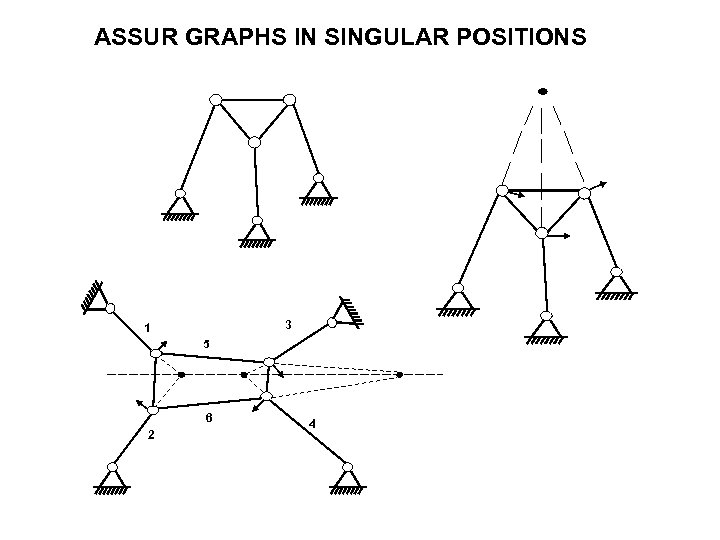ASSUR GRAPHS IN SINGULAR POSITIONS 3 1 5 6 2 4

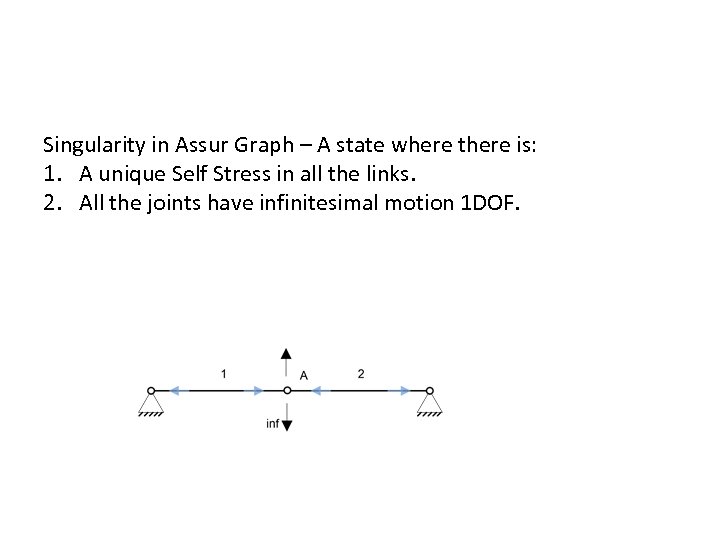Singularity in Assur Graph – A state where there is: 1. A unique Self Stress in all the links. 2. All the joints have infinitesimal motion 1 DOF.

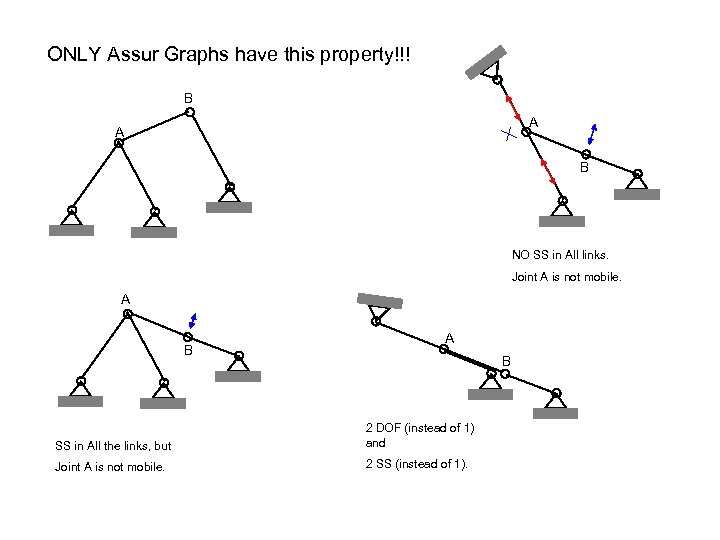ONLY Assur Graphs have this property!!! B A A B NO SS in All links. Joint A is not mobile. A B SS in All the links, but 2 DOF (instead of 1) and Joint A is not mobile. 2 SS (instead of 1).

Assur Graph + Singularity + Tensegrity Assur Graph at the singular position There is a unique self-stress in all the links Check the possibility: tension cables. compression struts.

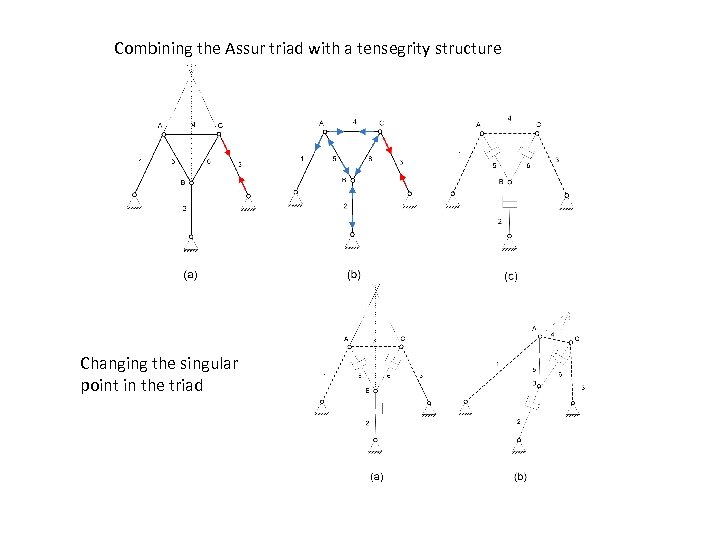Combining the Assur triad with a tensegrity structure Changing the singular point in the triad

From Soft to Rigid Structure Theorem: it is enough to change the location of only one element so that the Assur Truss is at the singular position. In case the structure is loose (soft) it is enough to shorten the length of only one cable so that the Assur Truss is being at the singular position.

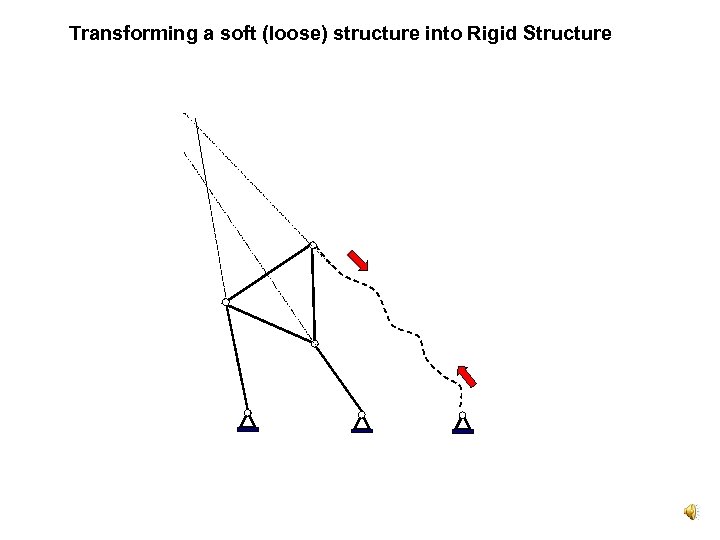Transforming a soft (loose) structure into Rigid Structure

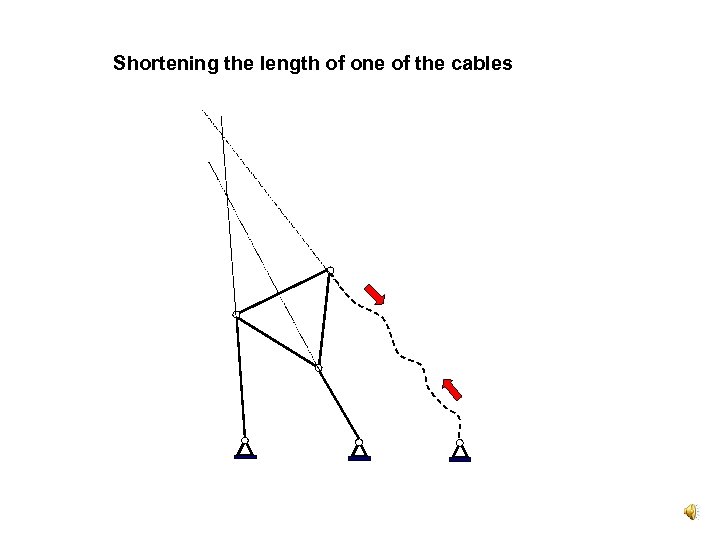Shortening the length of one of the cables

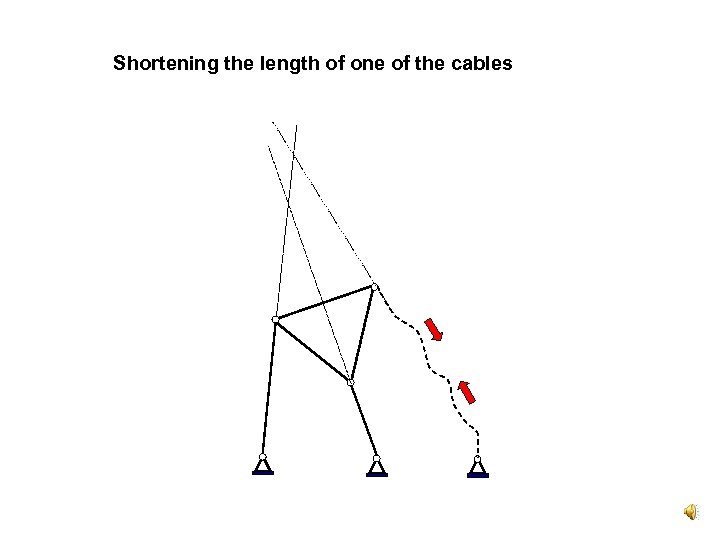Shortening the length of one of the cables

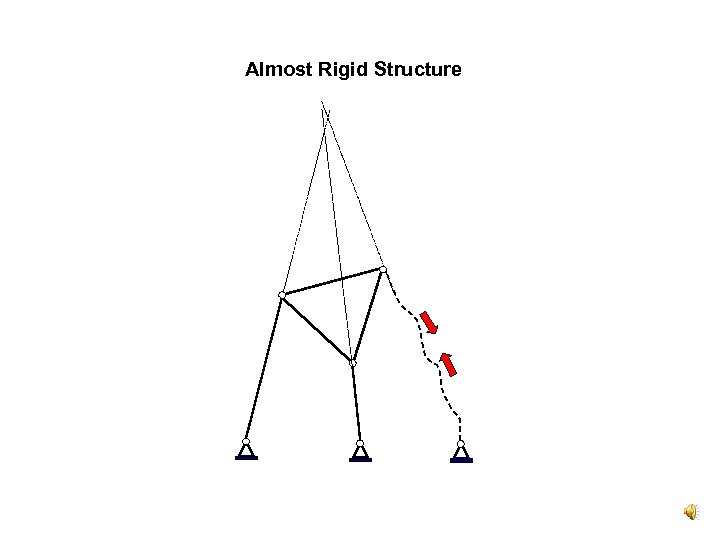Almost Rigid Structure

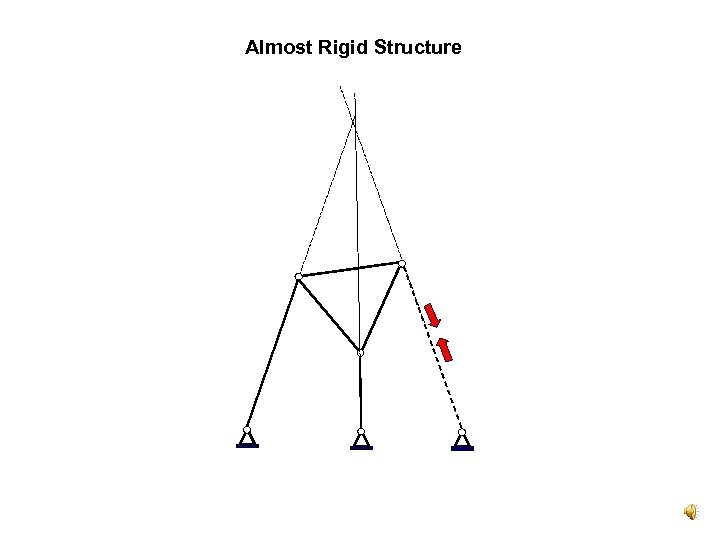Almost Rigid Structure

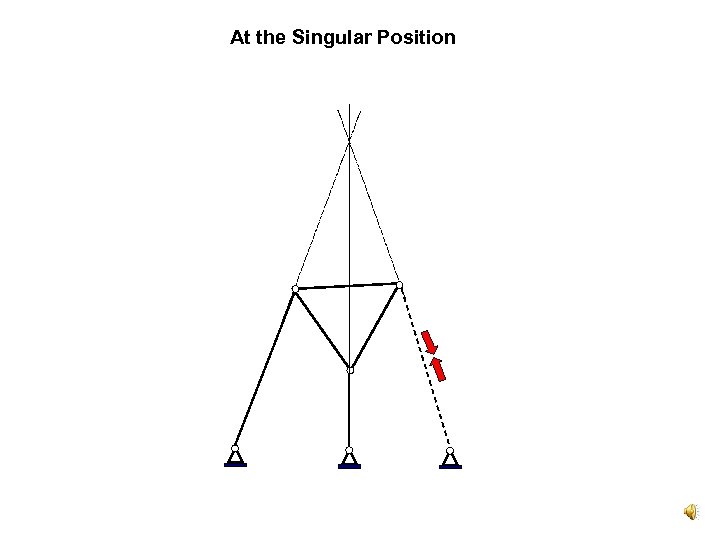At the Singular Position

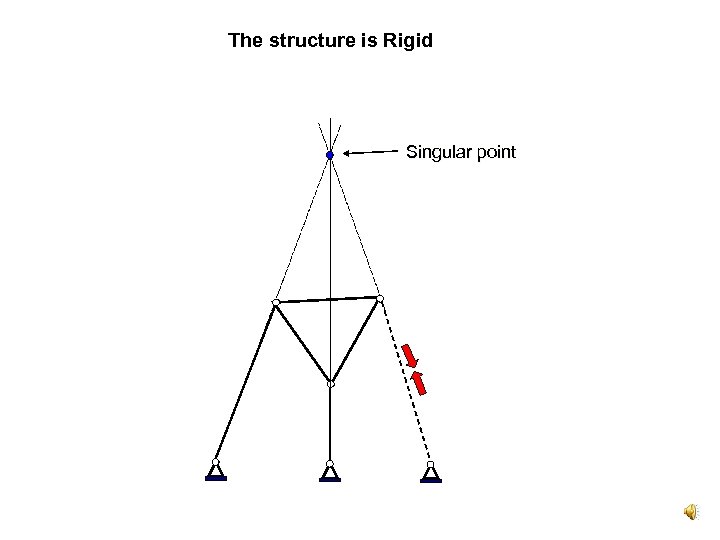The structure is Rigid Singular point

The First type of robot that employs the three properties: 1. Assur Graph. 2. Tensegrity. 3. Singularity.

Adjustable Deployable Tensegrity Structure – A structure that can deploy and fold but all the time is rigid, i. e. , can sustain external forces. This property is obtained by constantly maintaining the structure at the singular position!

Deployed system Folded system

The Second type of robot that relies on these three properties: 1. Assur Graph. 2. Tensegrity. 3. Singularity. Animal (caterpillar) robot.

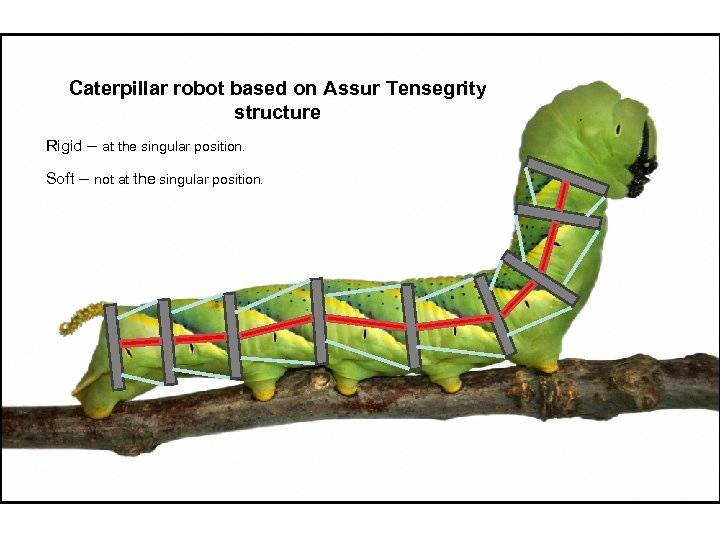Caterpillar robot based on Assur Tensegrity structure Rigid – at the singular position. Soft – not at the singular position.

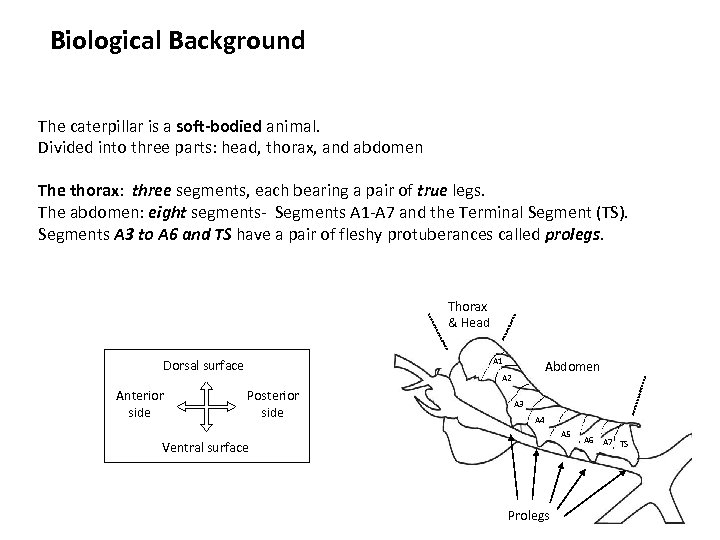Biological Background The caterpillar is a soft-bodied animal. Divided into three parts: head, thorax, and abdomen The thorax: three segments, each bearing a pair of true legs. The abdomen: eight segments- Segments A 1 -A 7 and the Terminal Segment (TS). Segments A 3 to A 6 and TS have a pair of fleshy protuberances called prolegs. Thorax & Head A 1 Dorsal surface Anterior side Abdomen A 2 Posterior side A 3 A 4 A 5 Ventral surface Prolegs A 6 A 7 TS

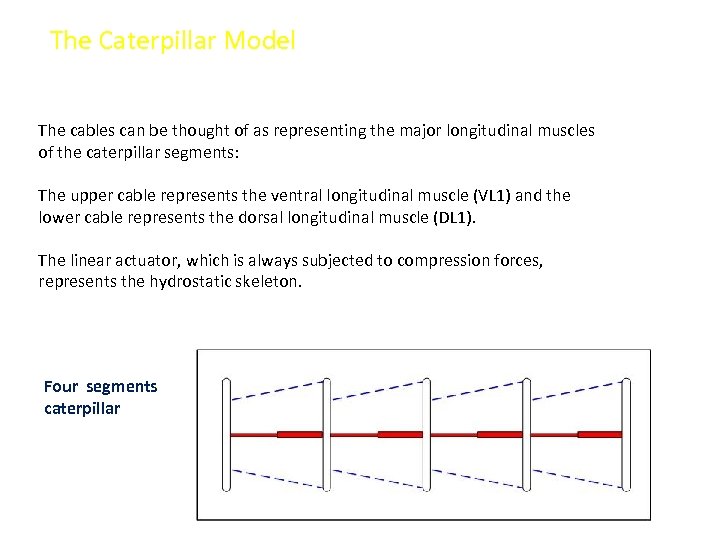The Caterpillar Model The cables can be thought of as representing the major longitudinal muscles of the caterpillar segments: The upper cable represents the ventral longitudinal muscle (VL 1) and the lower cable represents the dorsal longitudinal muscle (DL 1). The linear actuator, which is always subjected to compression forces, represents the hydrostatic skeleton. Four segments caterpillar

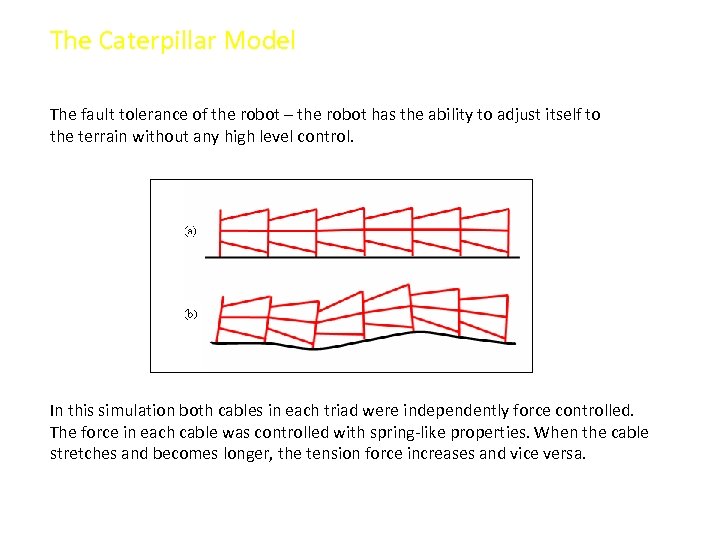The Caterpillar Model The fault tolerance of the robot – the robot has the ability to adjust itself to the terrain without any high level control. In this simulation both cables in each triad were independently force controlled. The force in each cable was controlled with spring-like properties. When the cable stretches and becomes longer, the tension force increases and vice versa.

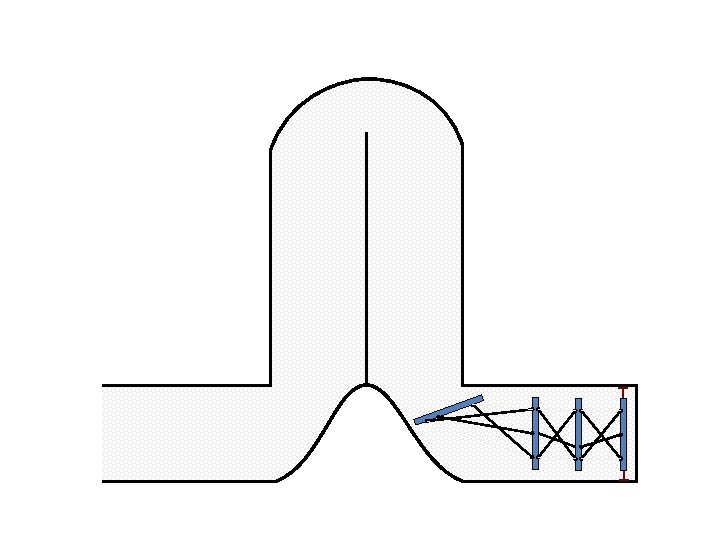
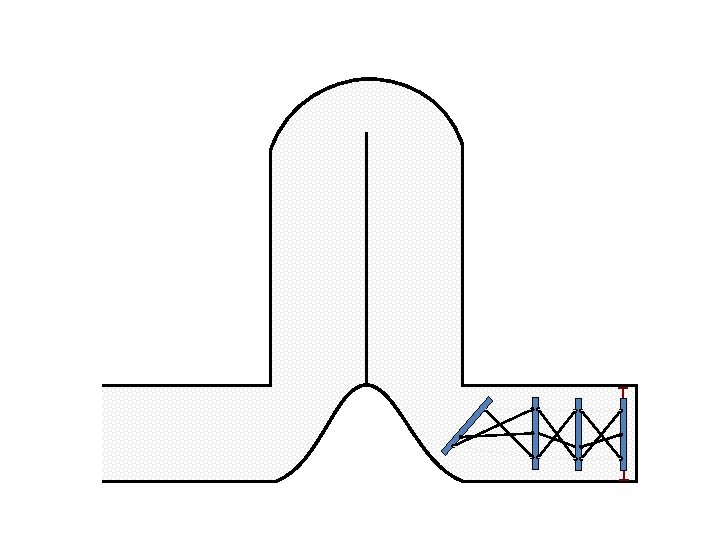
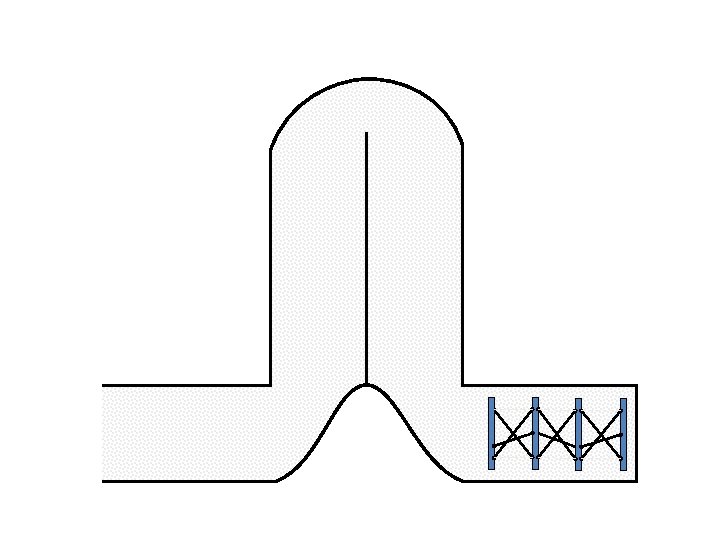
New Possible Application Crawling in Tunnels.

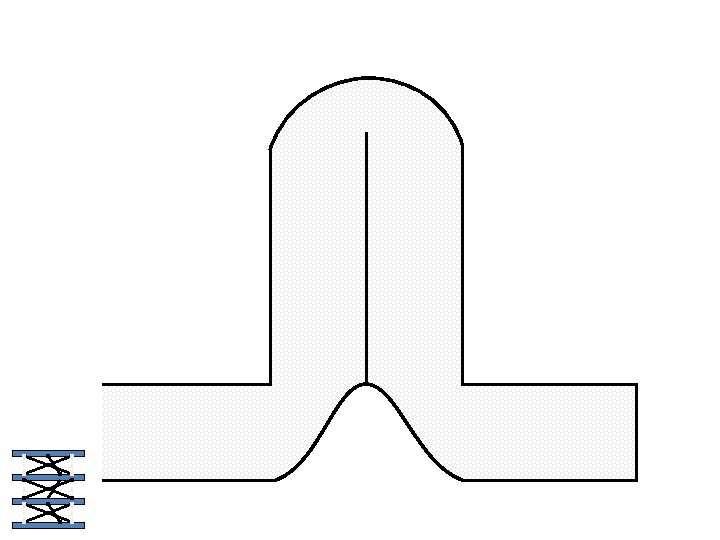
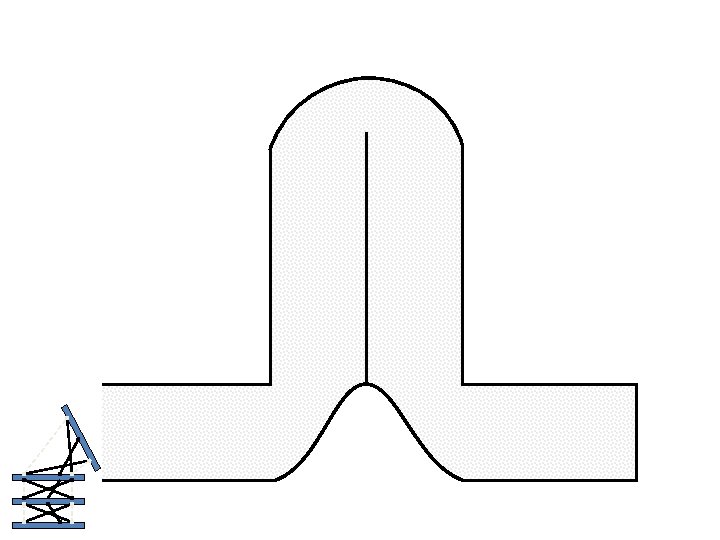
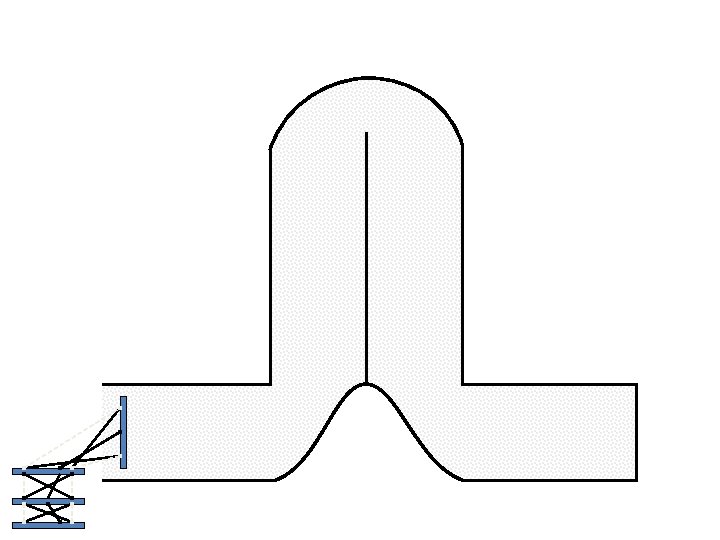
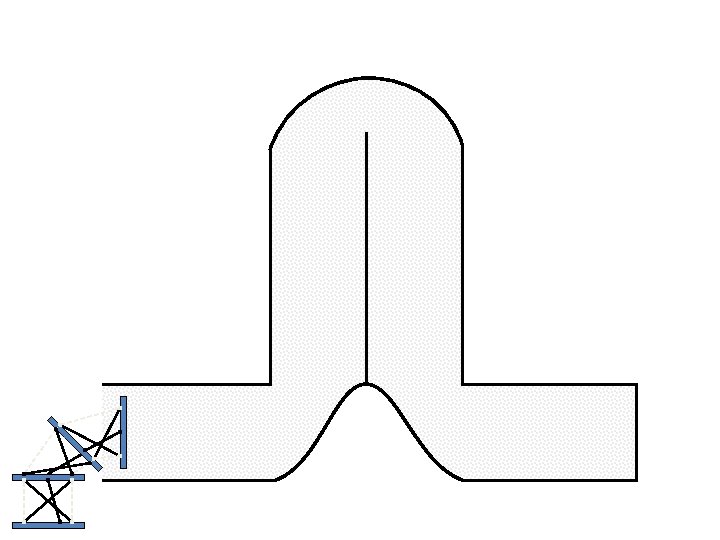
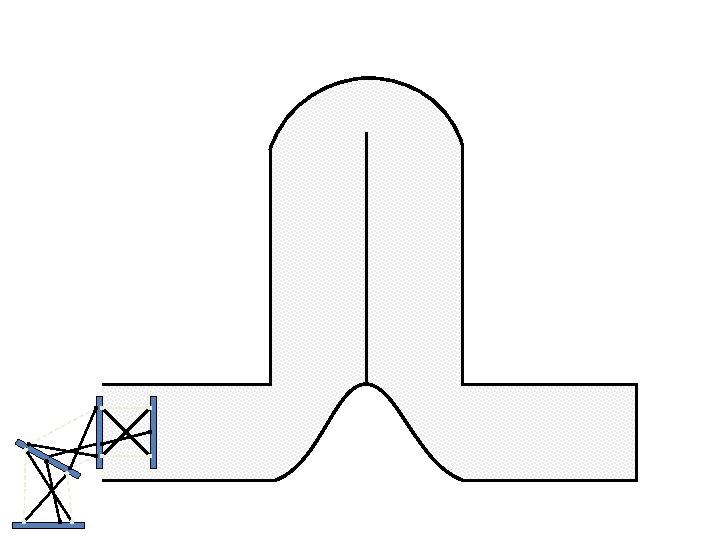
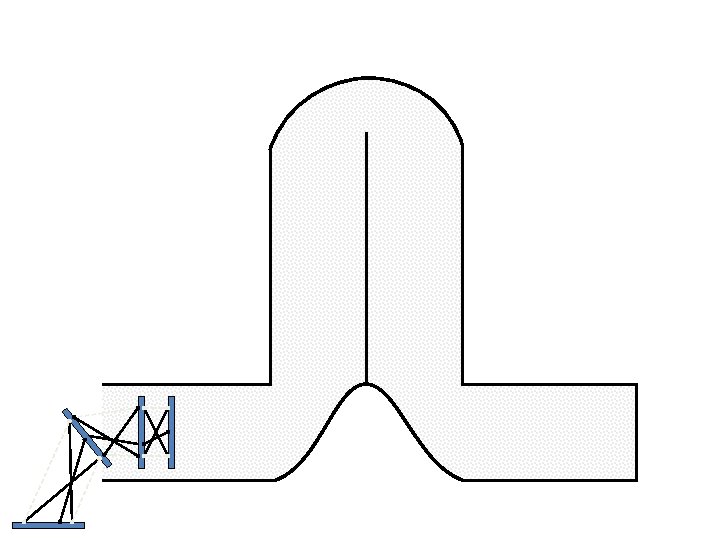
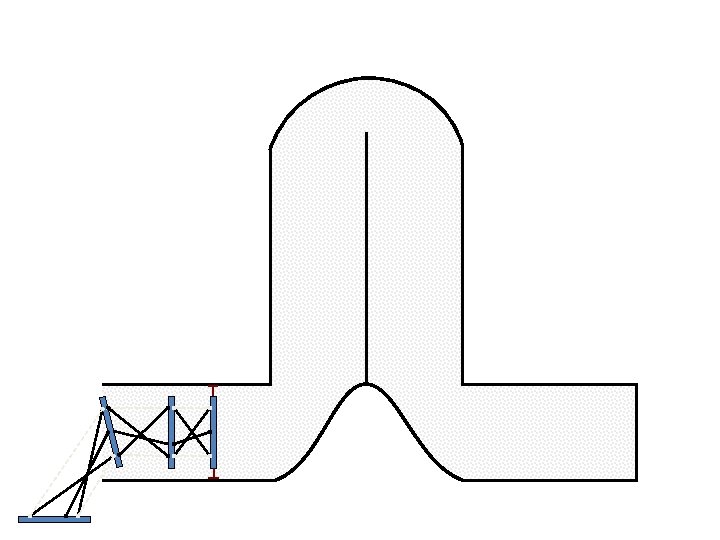
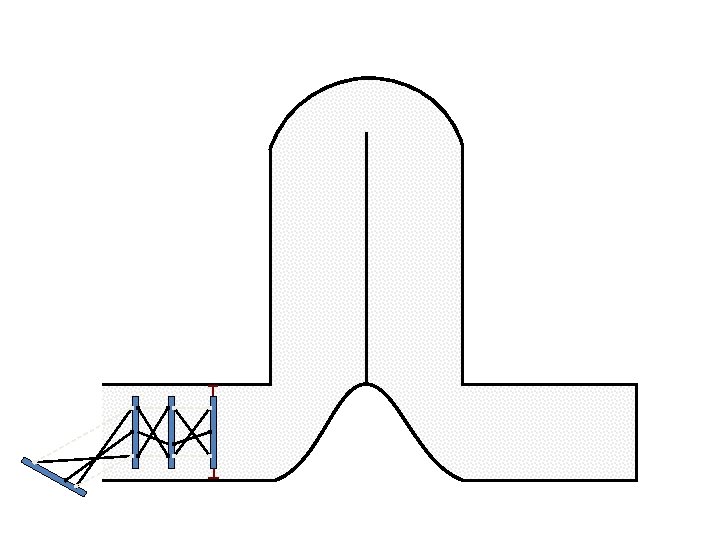
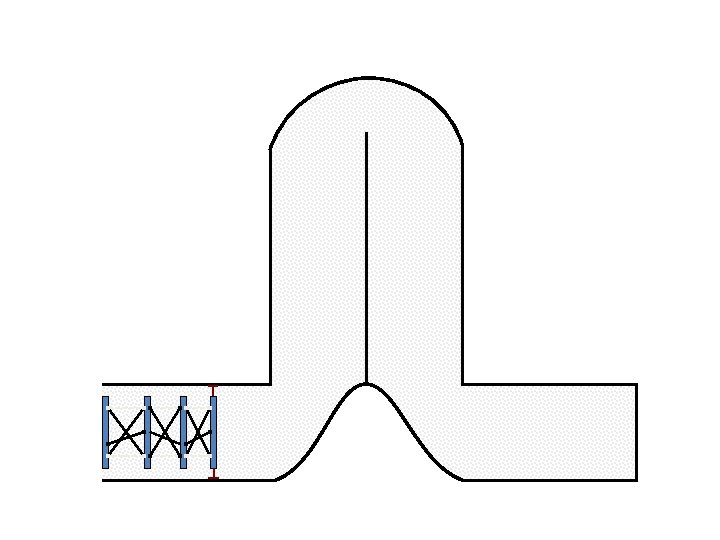
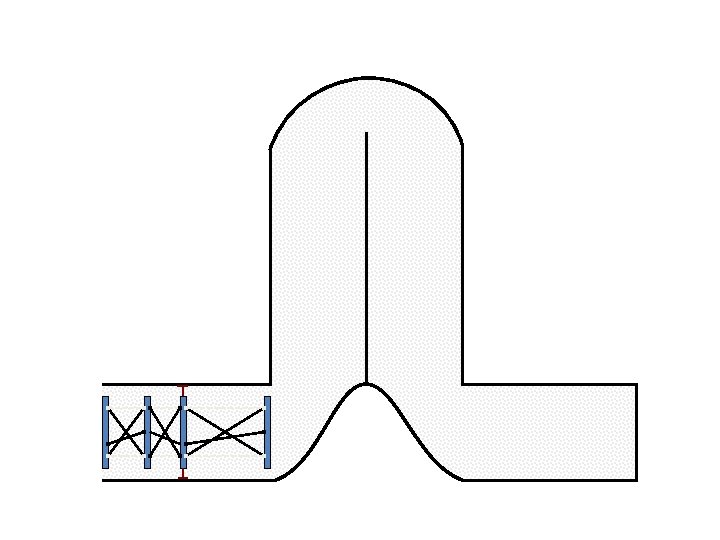
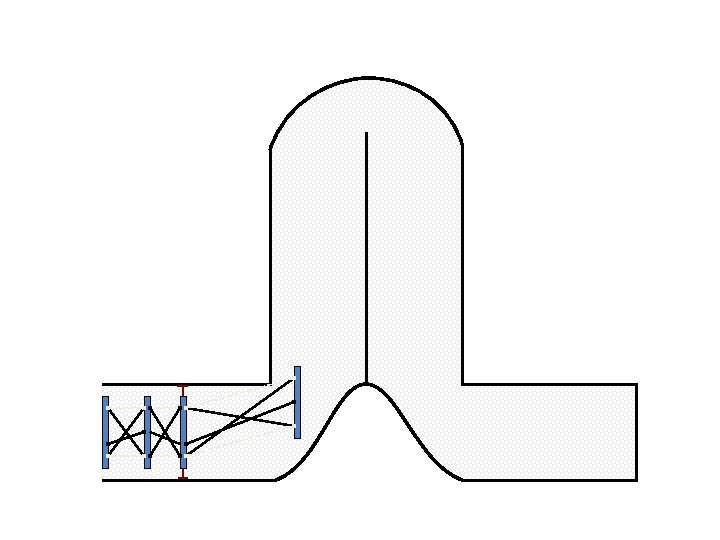
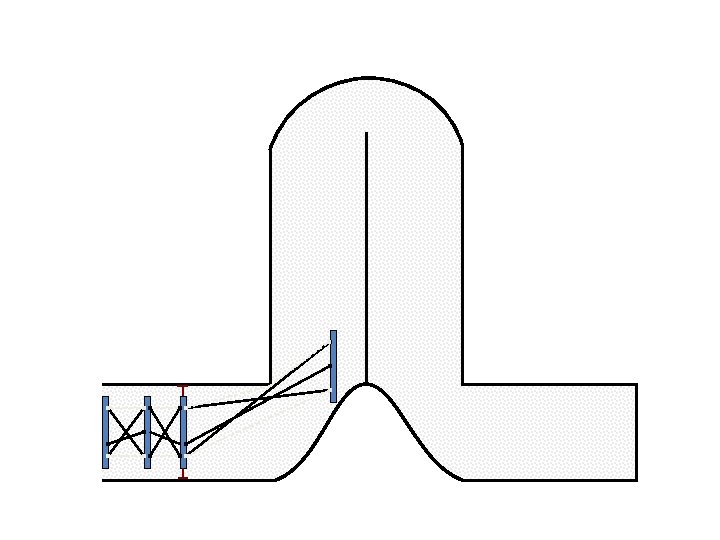
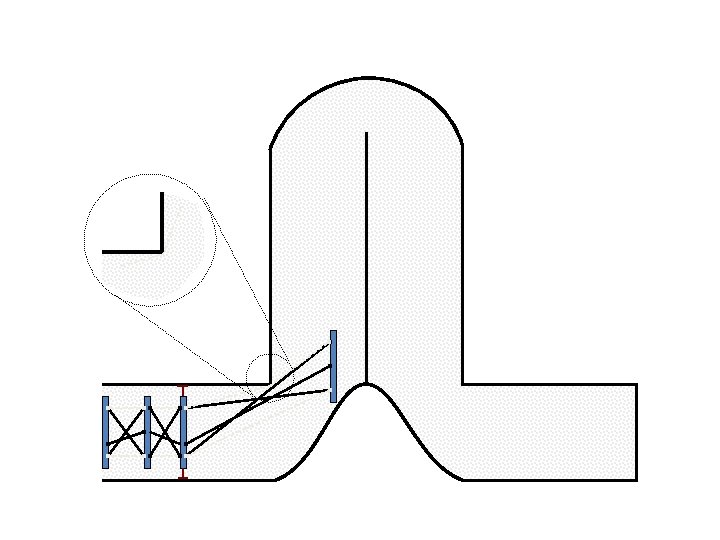
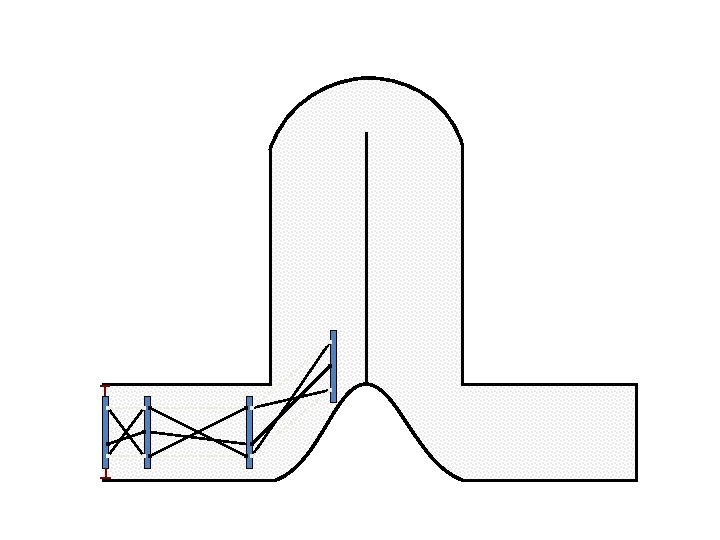
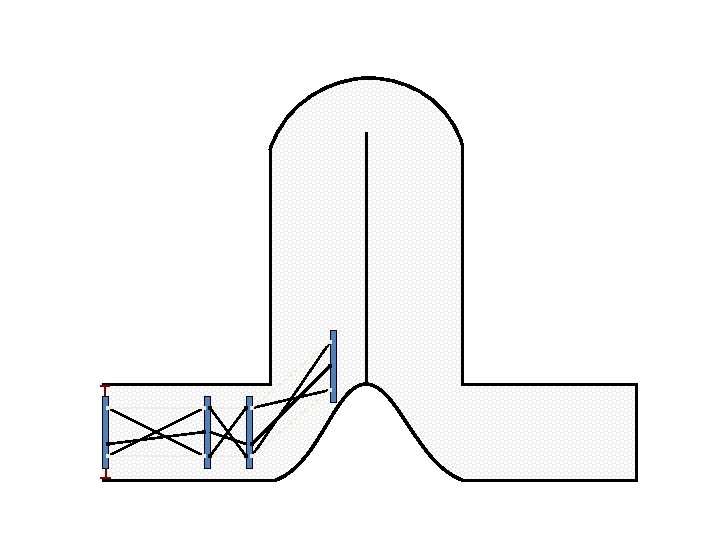
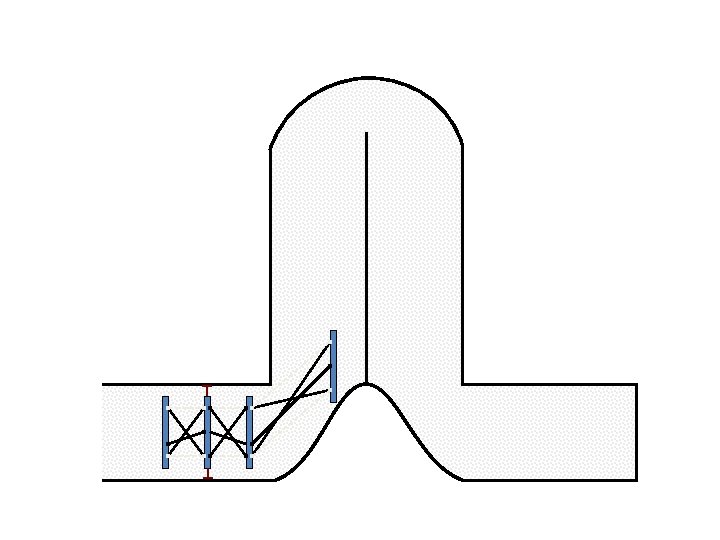
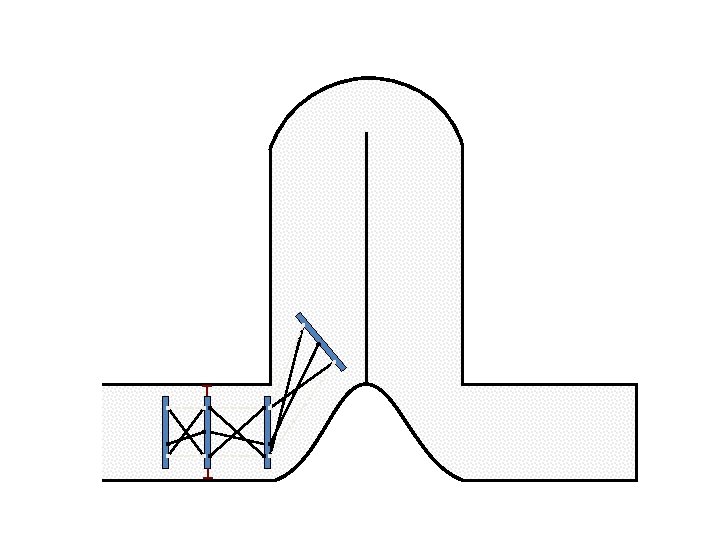
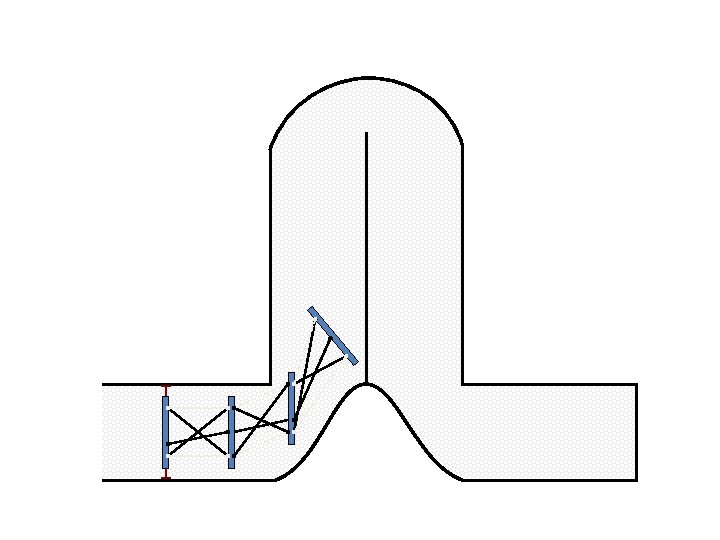
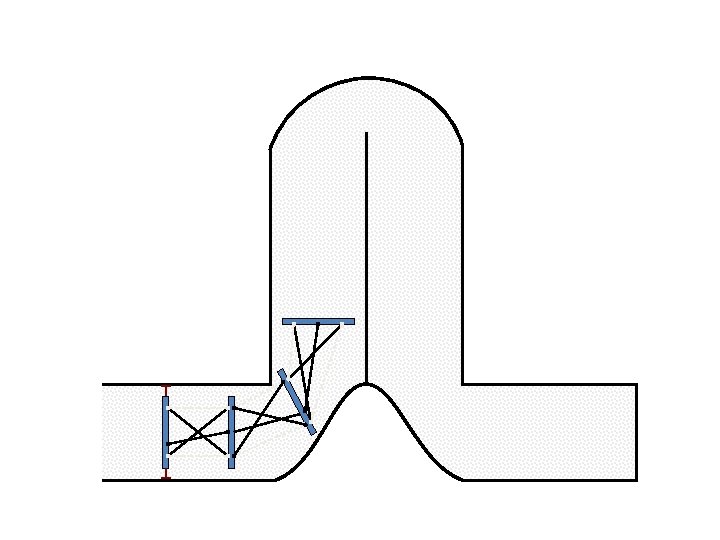
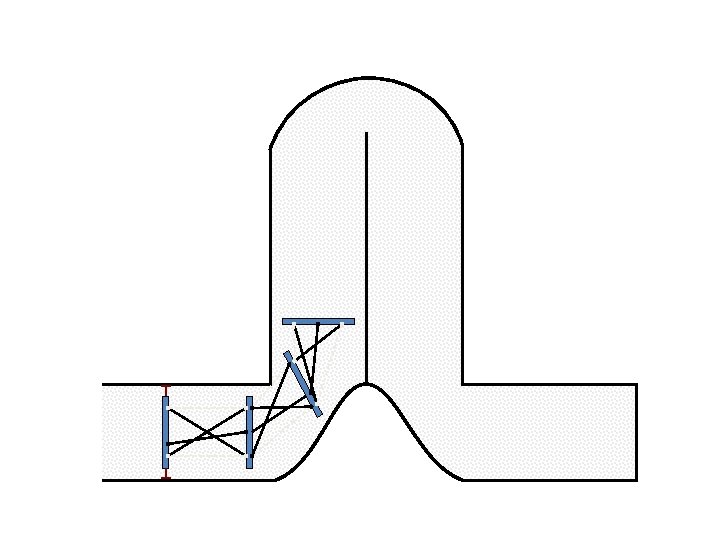
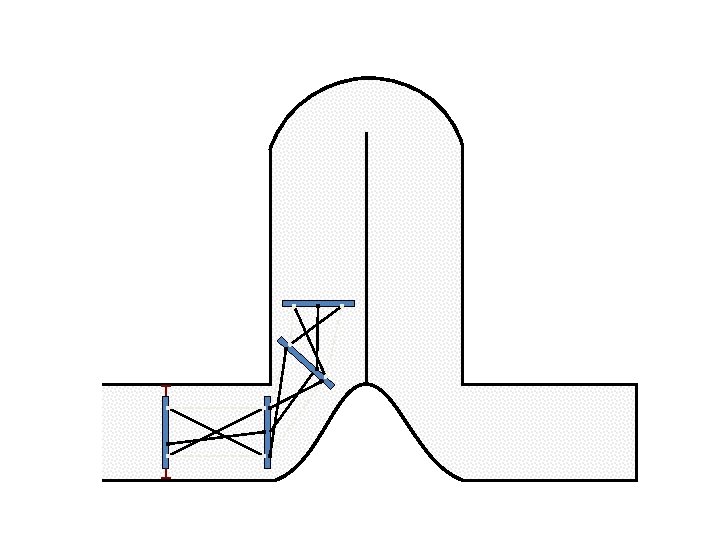
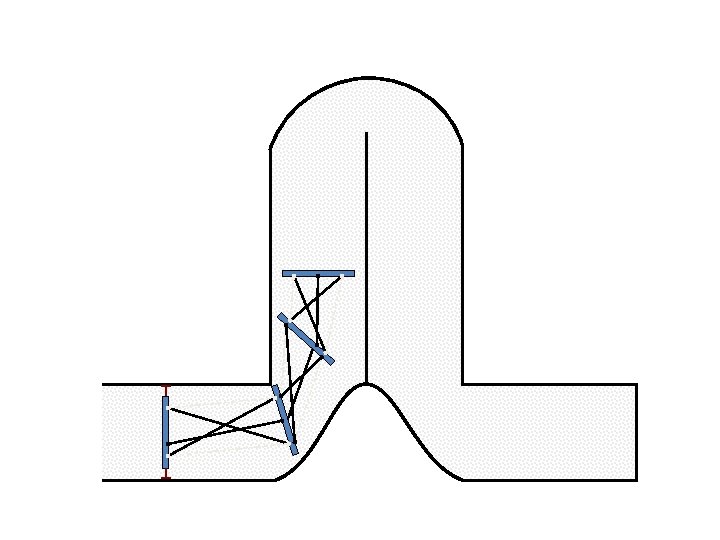
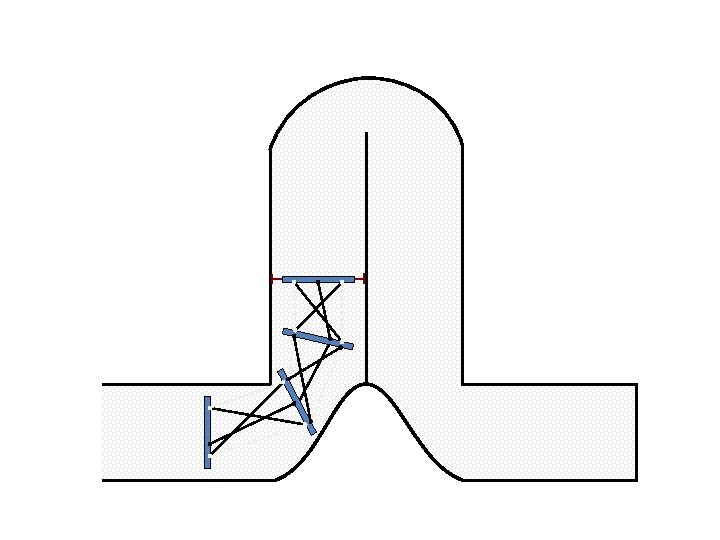
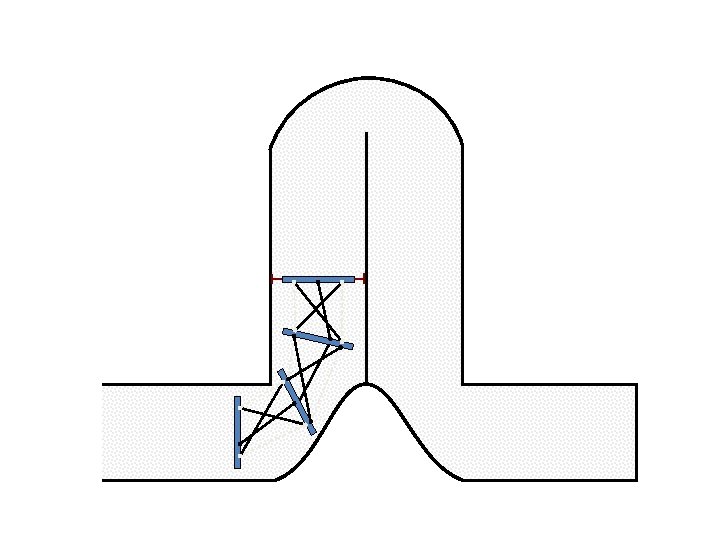
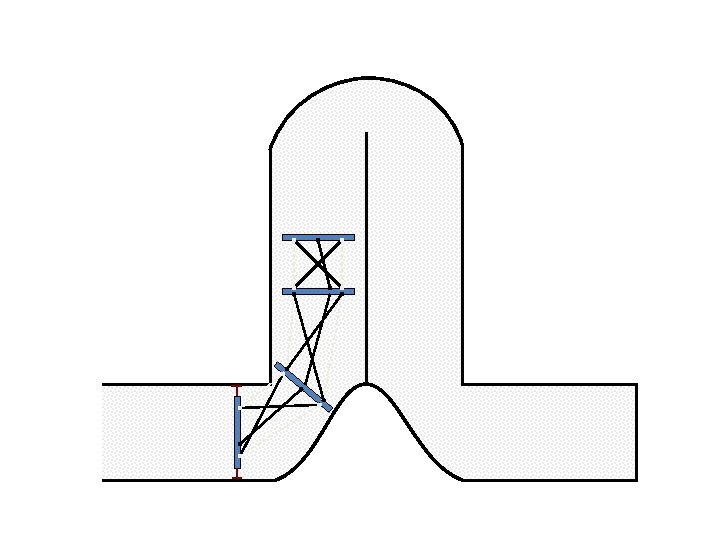
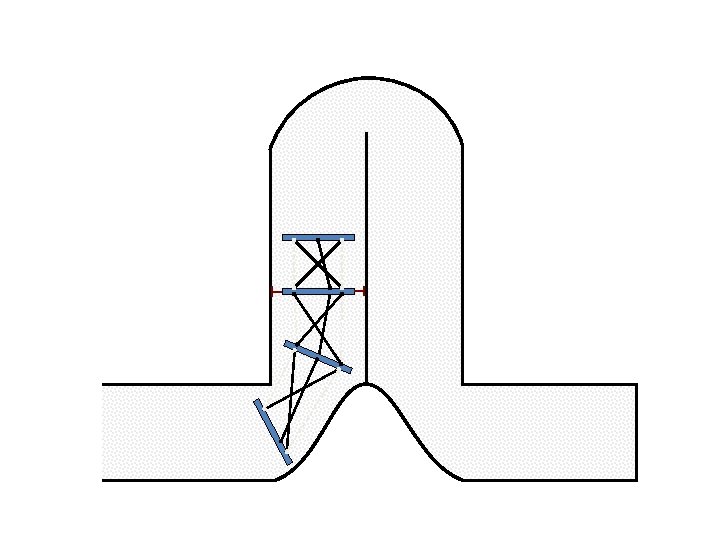
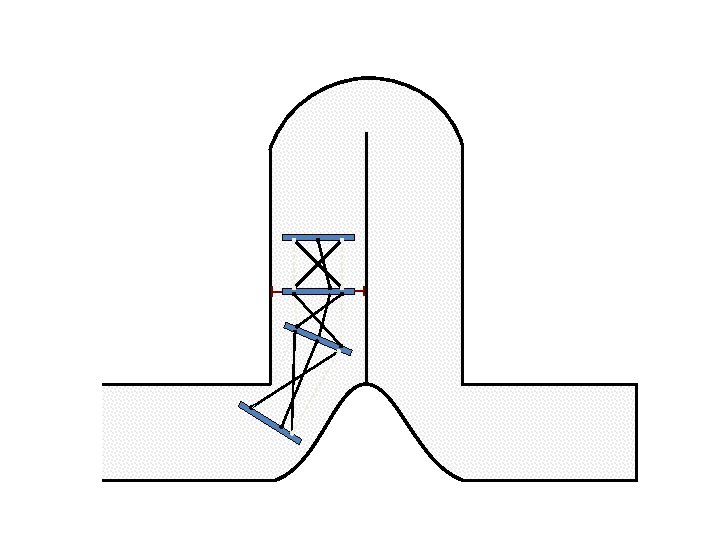
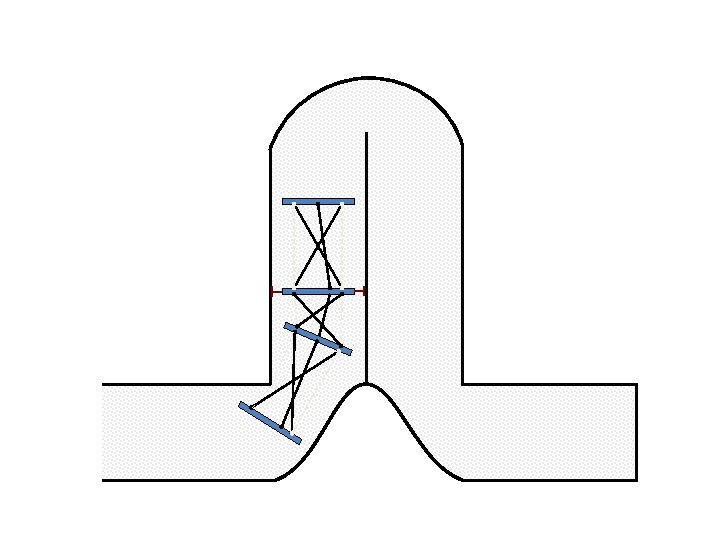
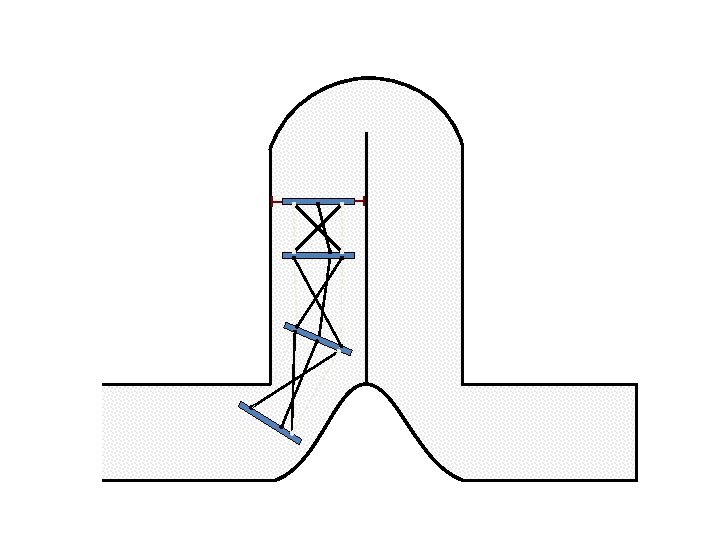
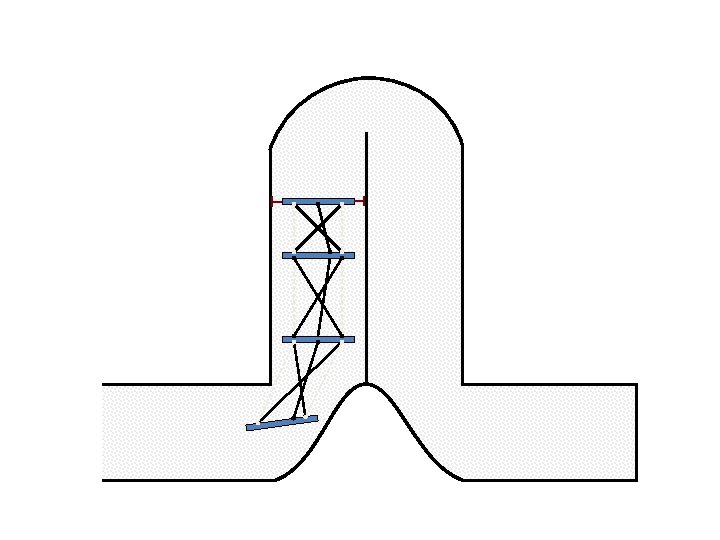
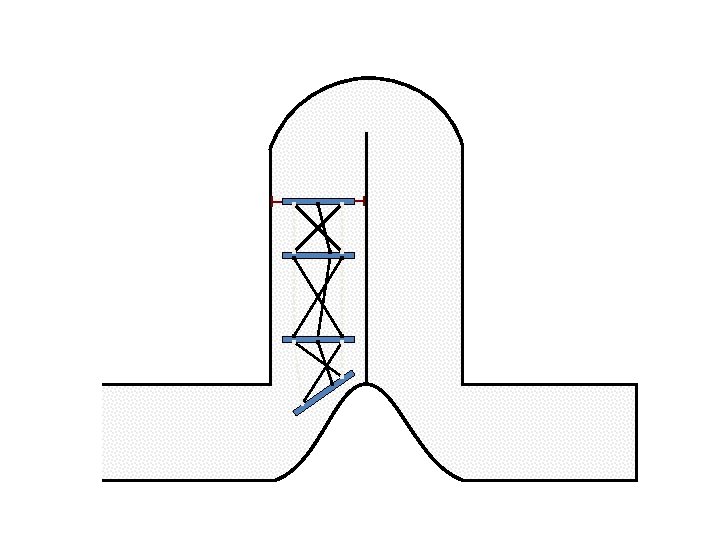
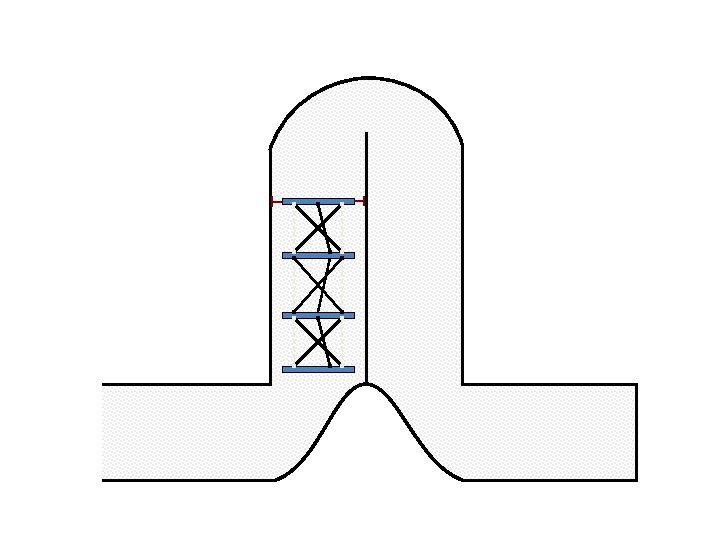
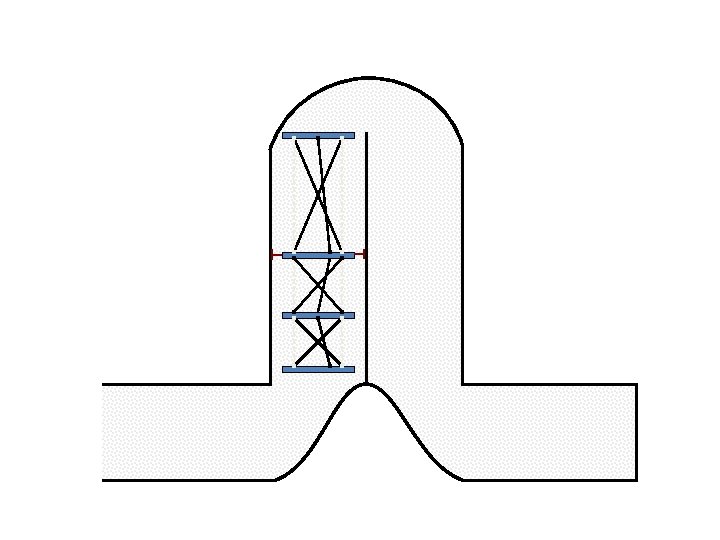
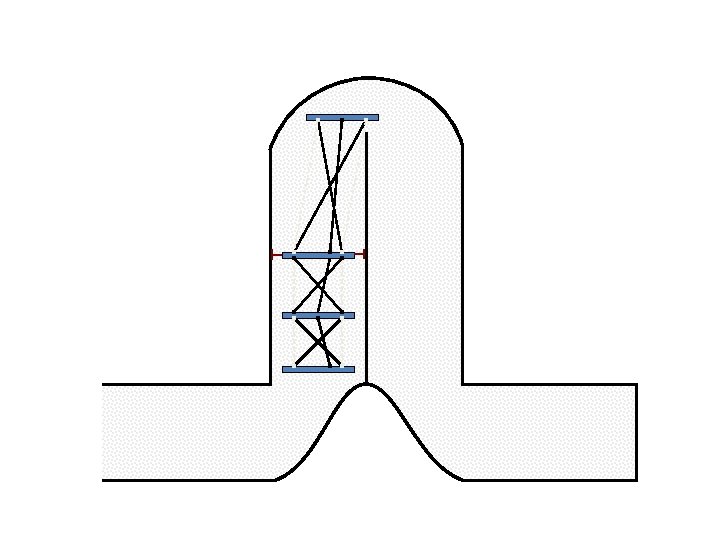
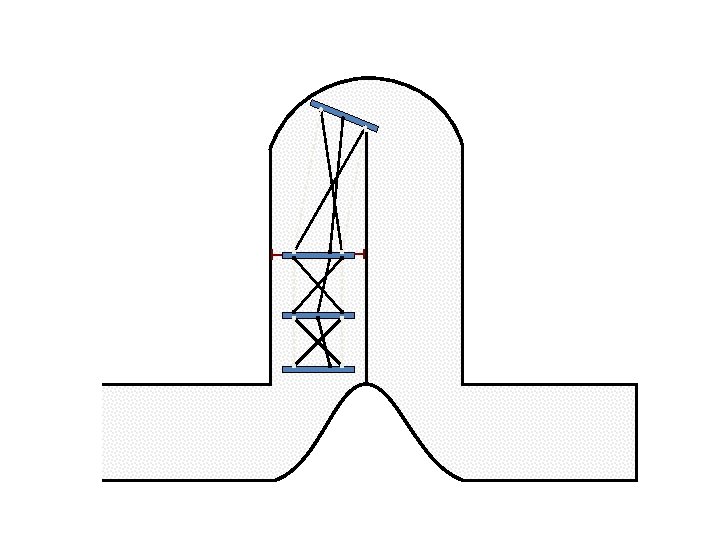
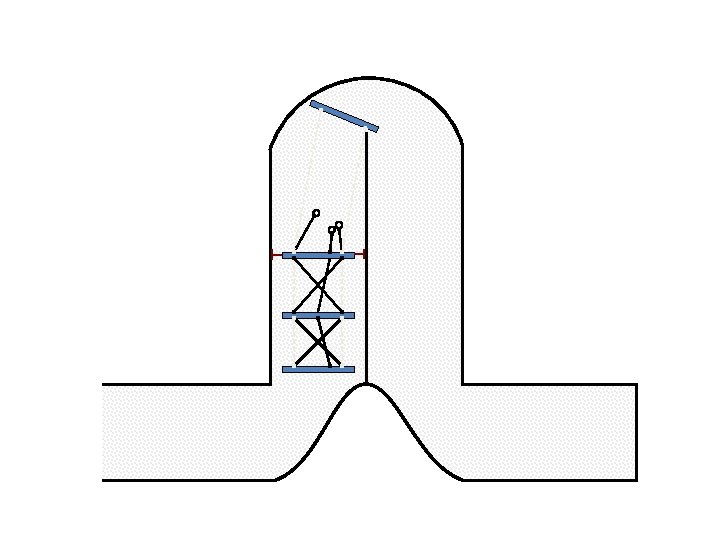
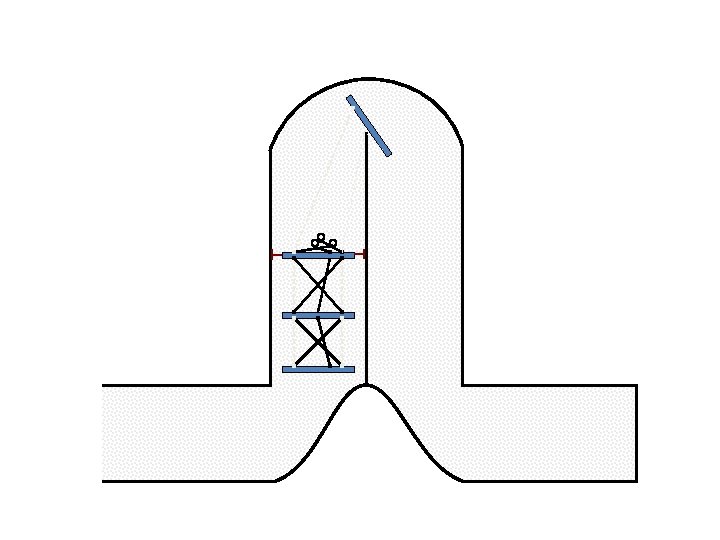
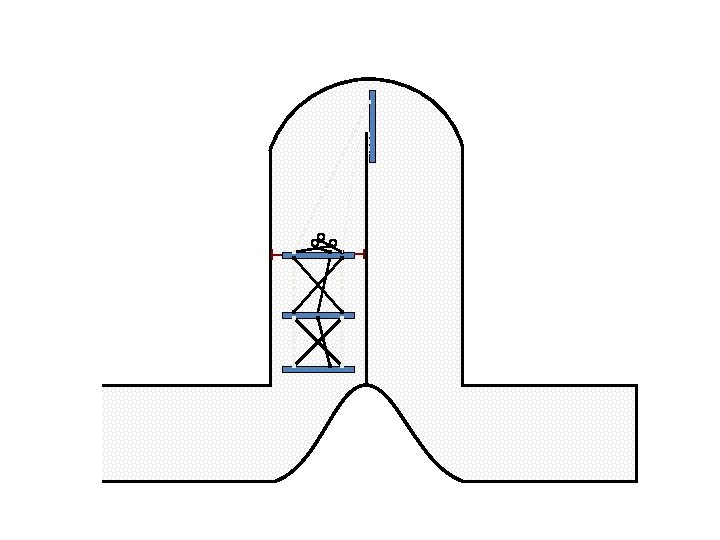
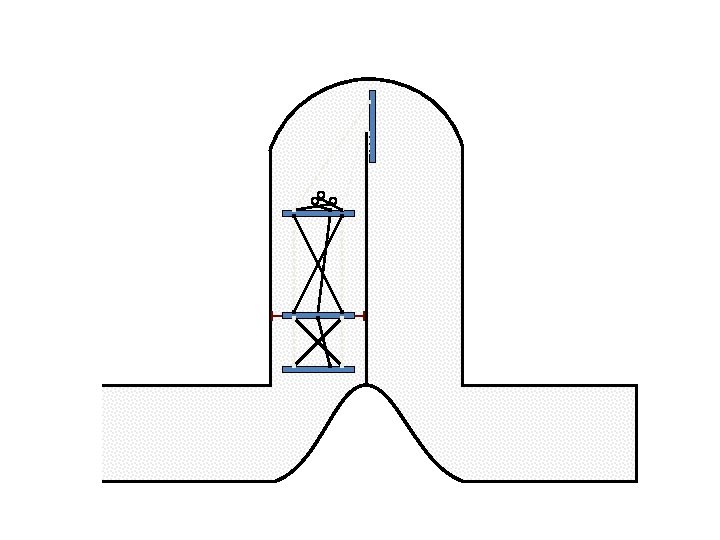
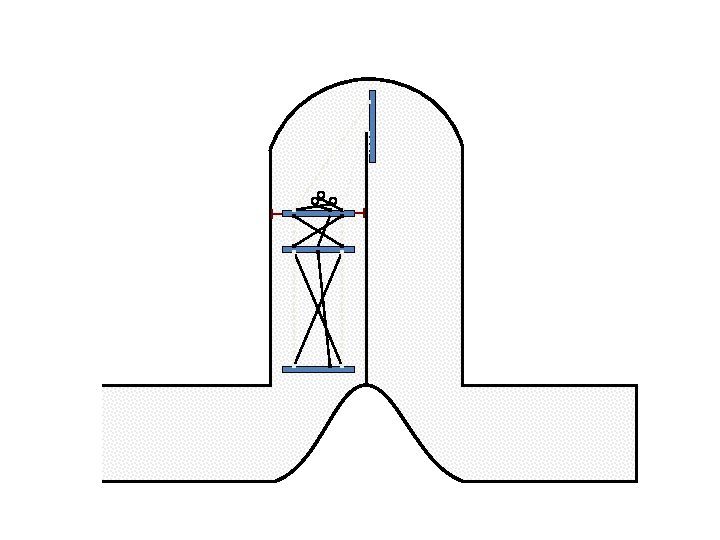
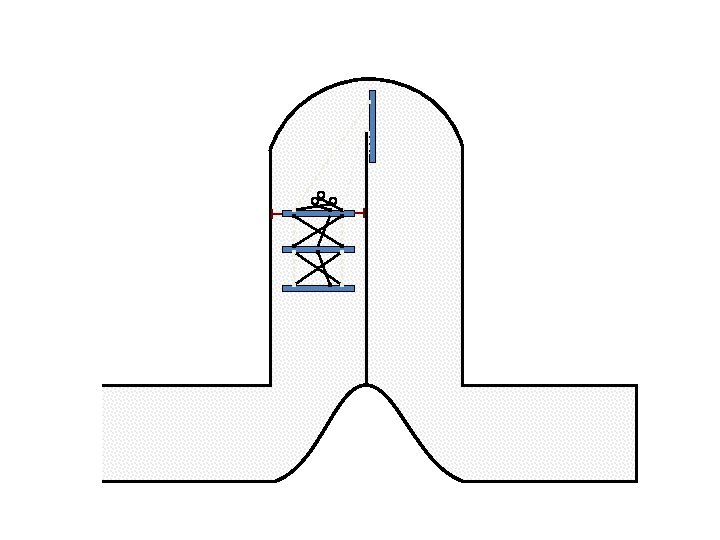
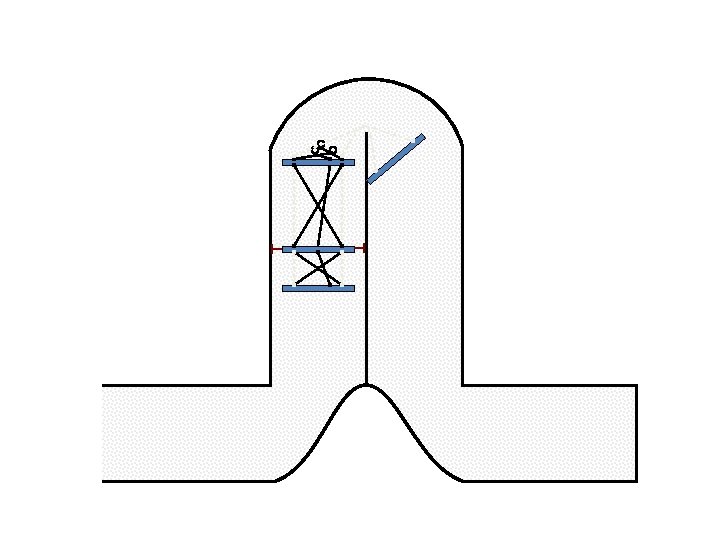
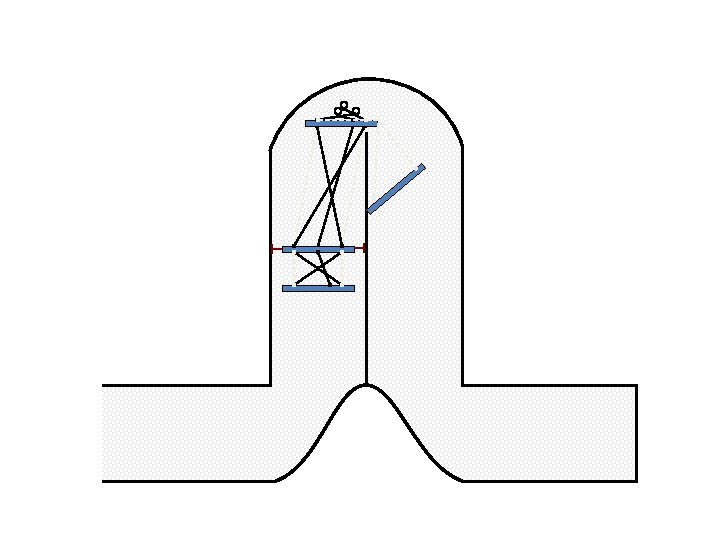
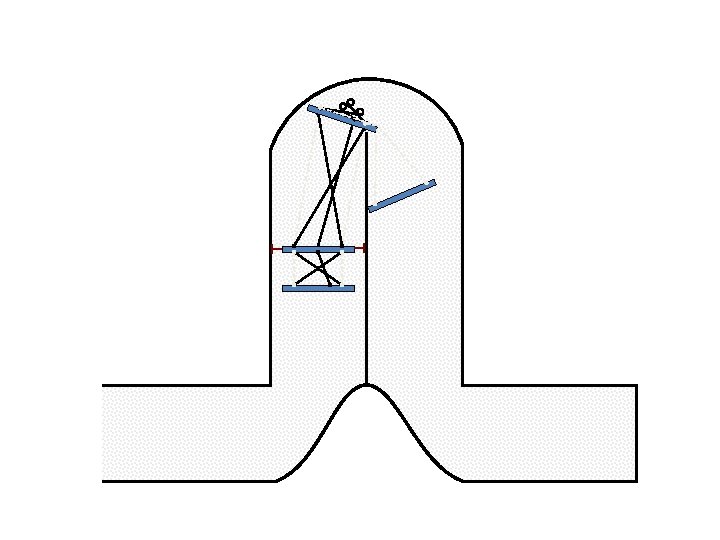
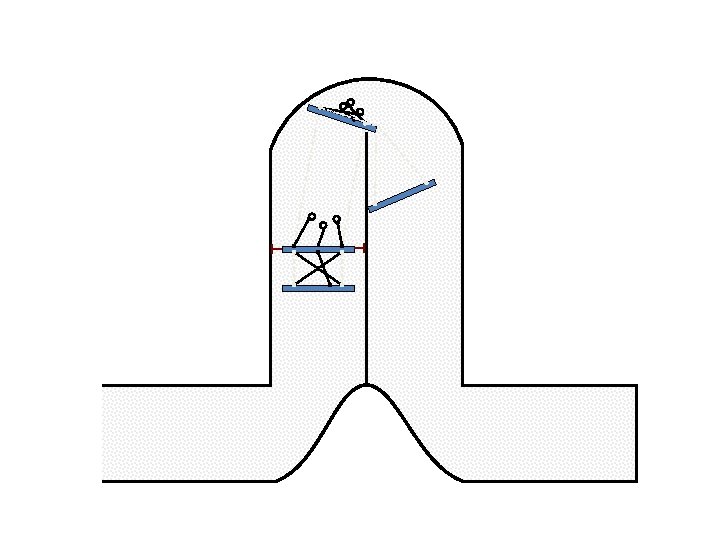
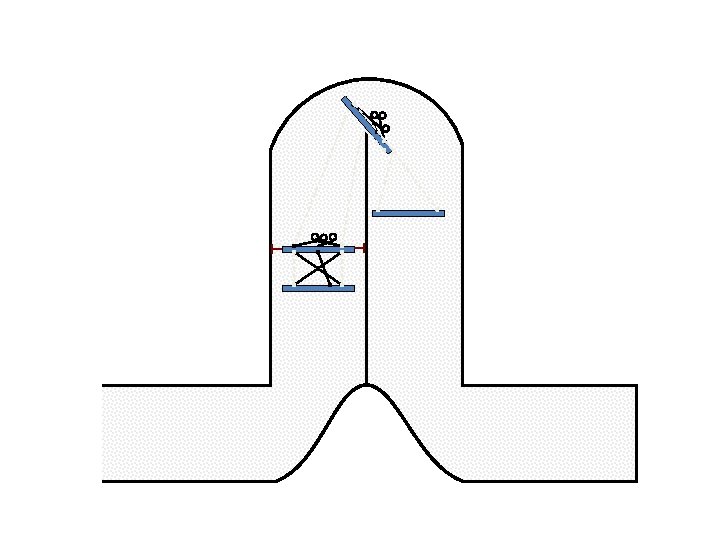
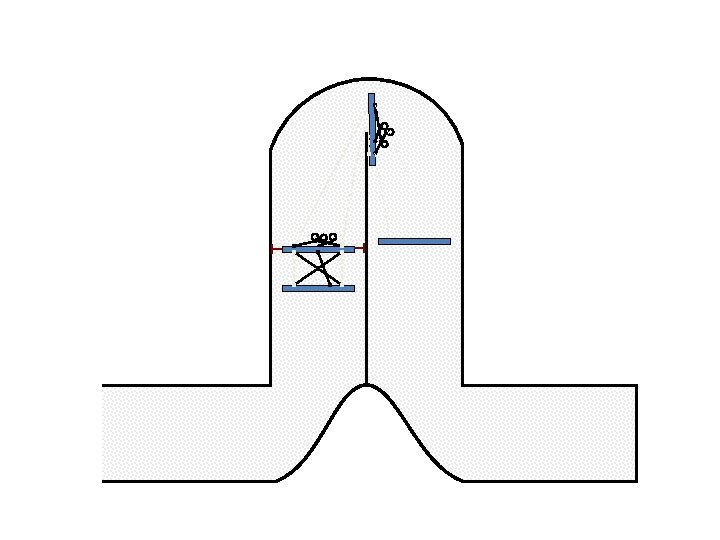
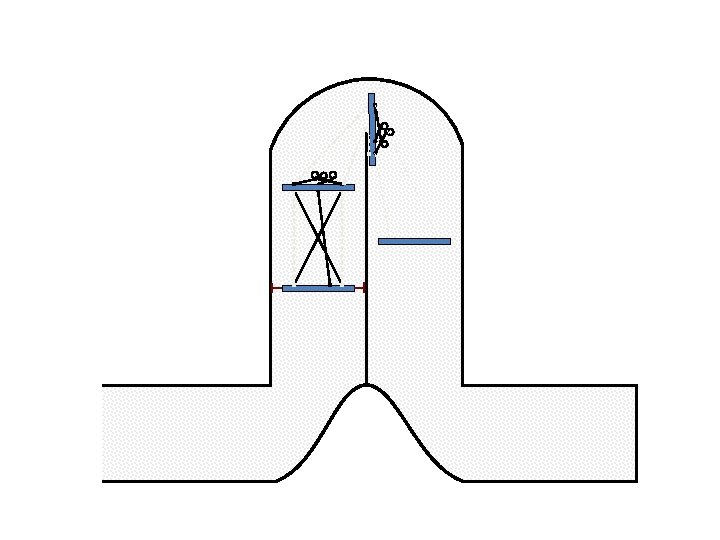
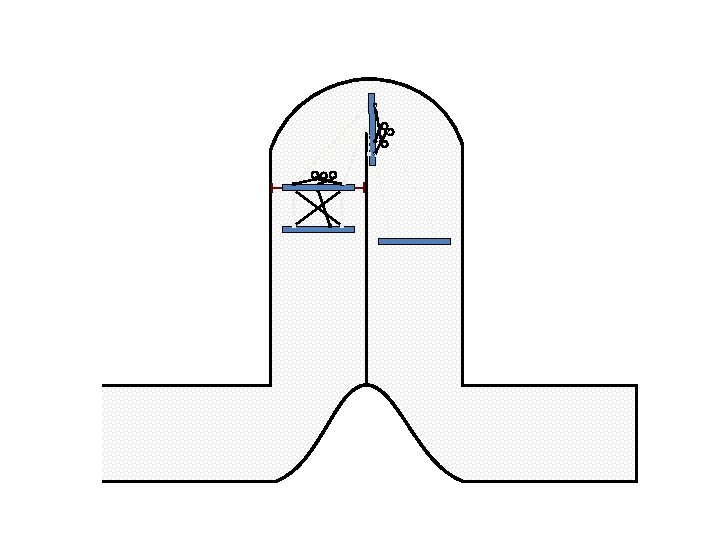
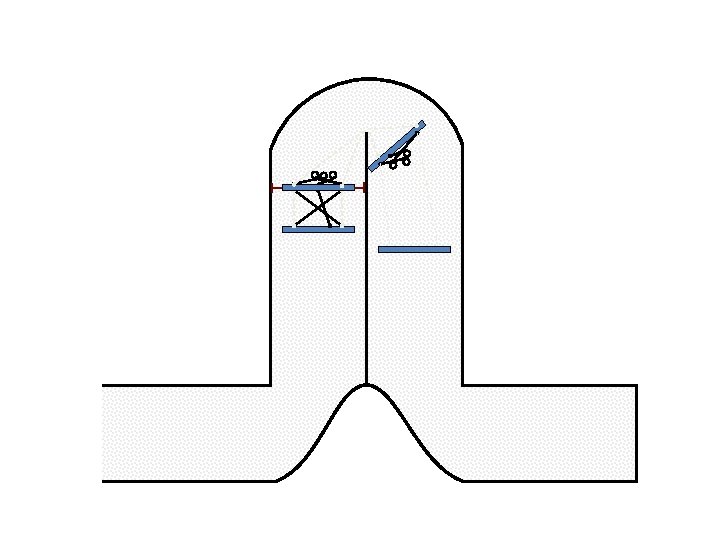
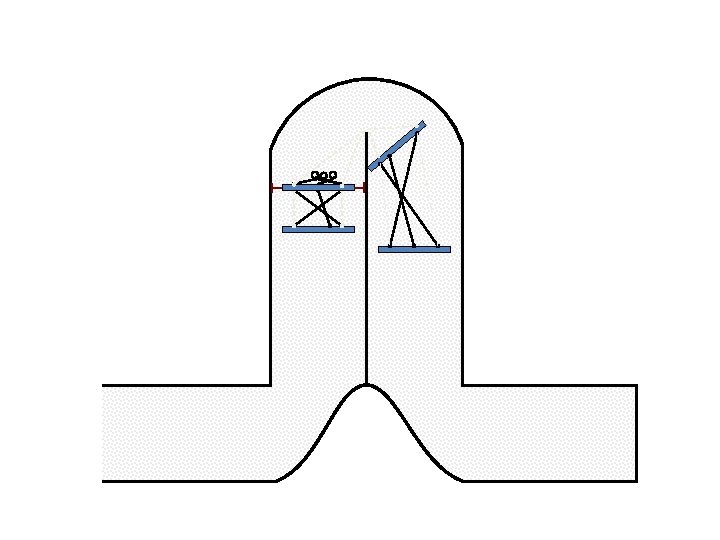
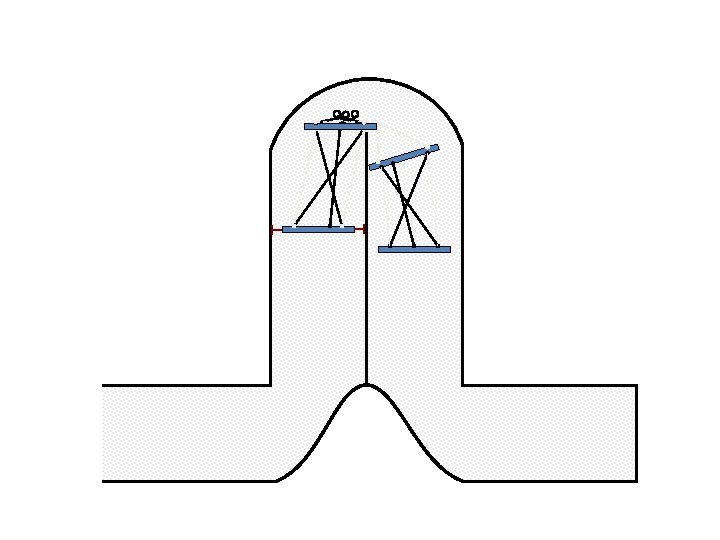
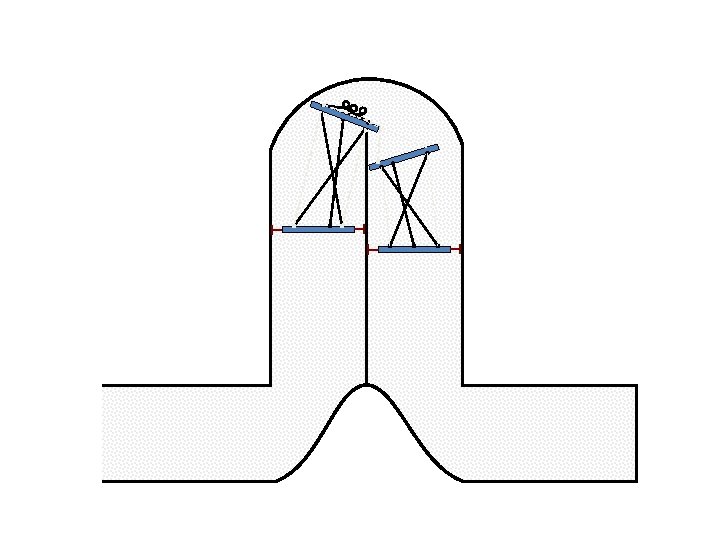
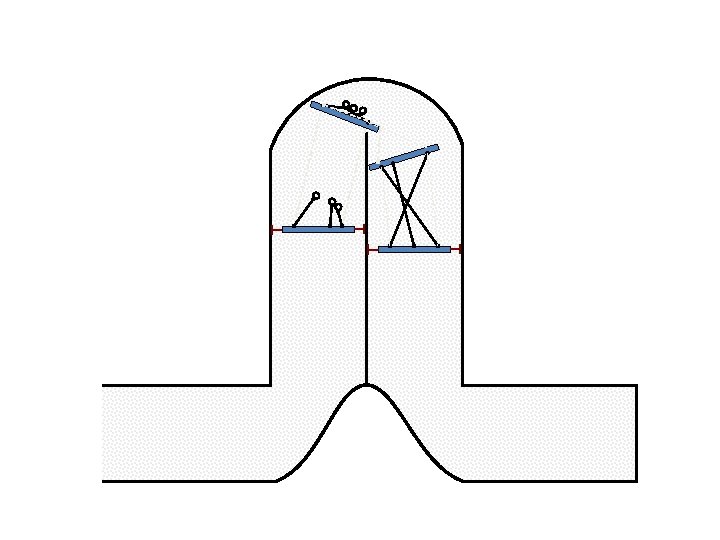
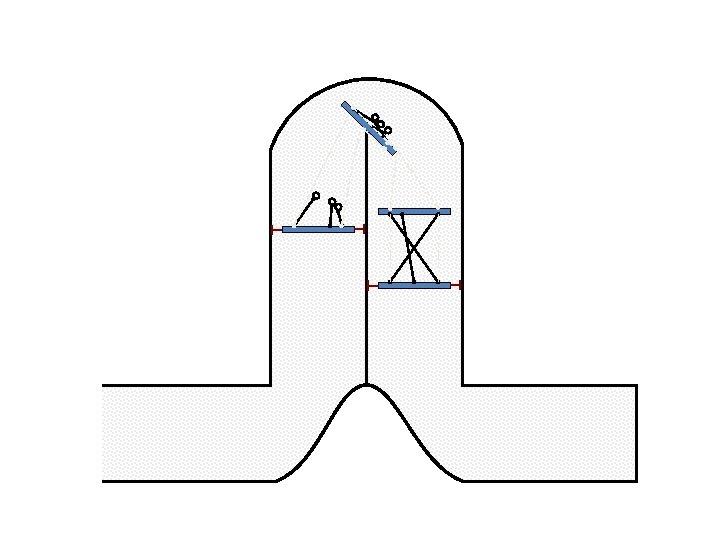
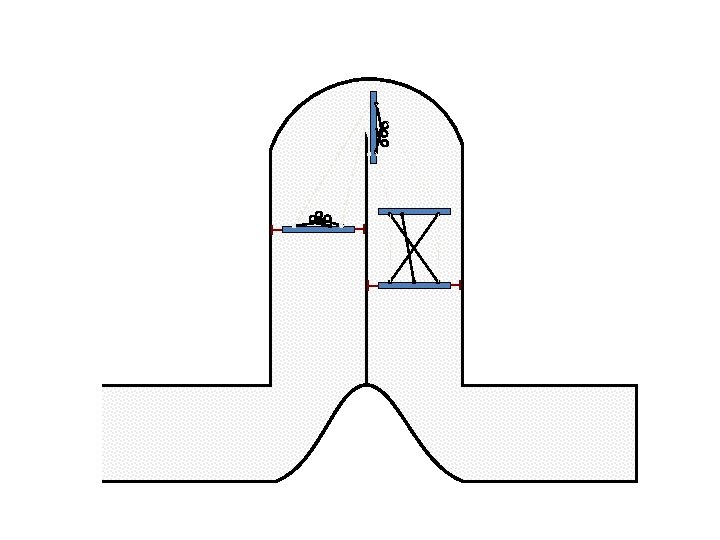
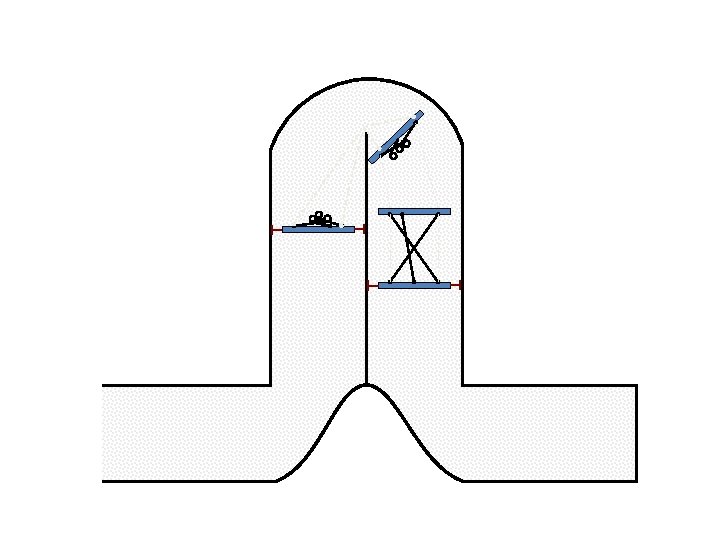
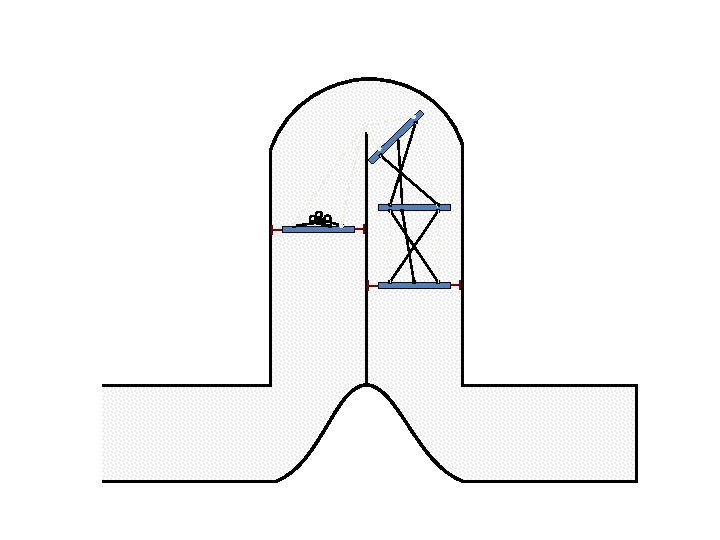
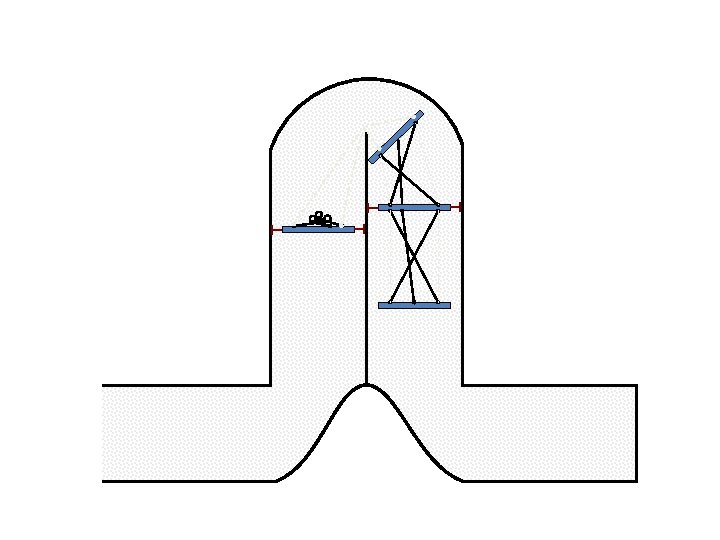
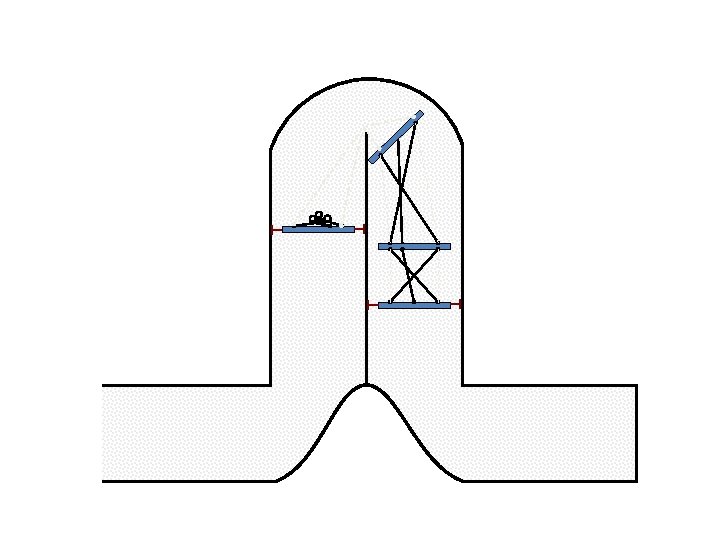
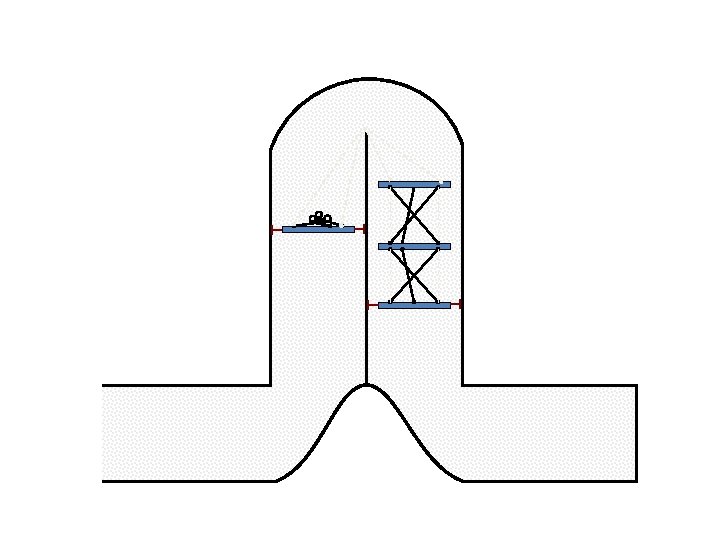
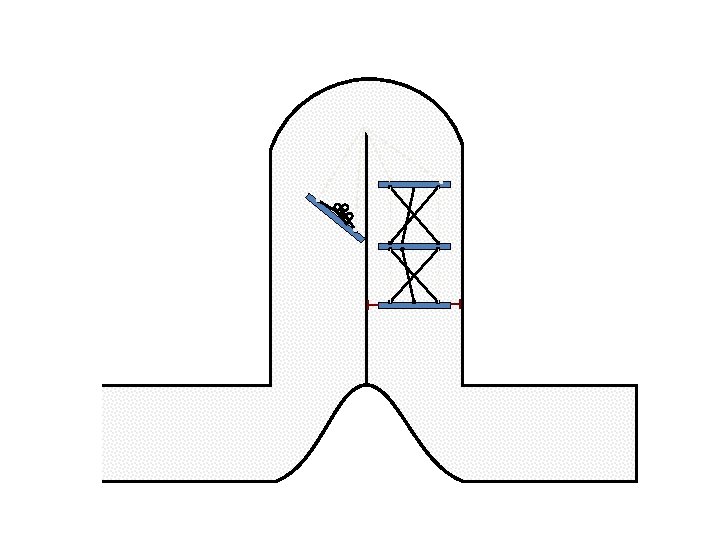
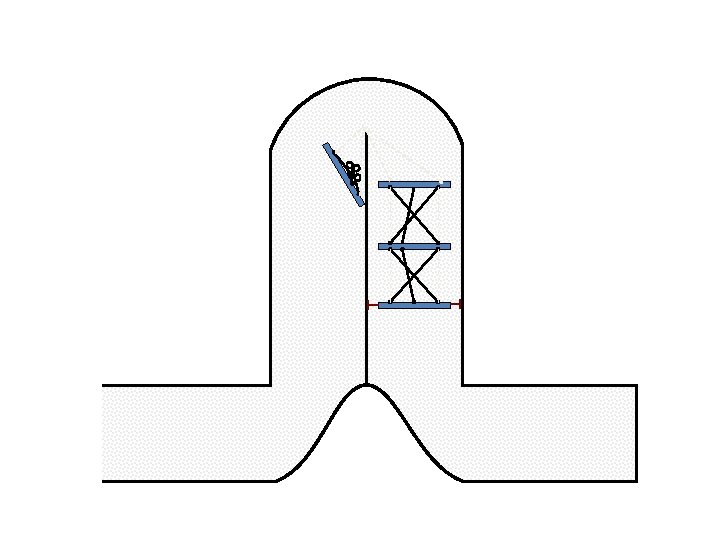
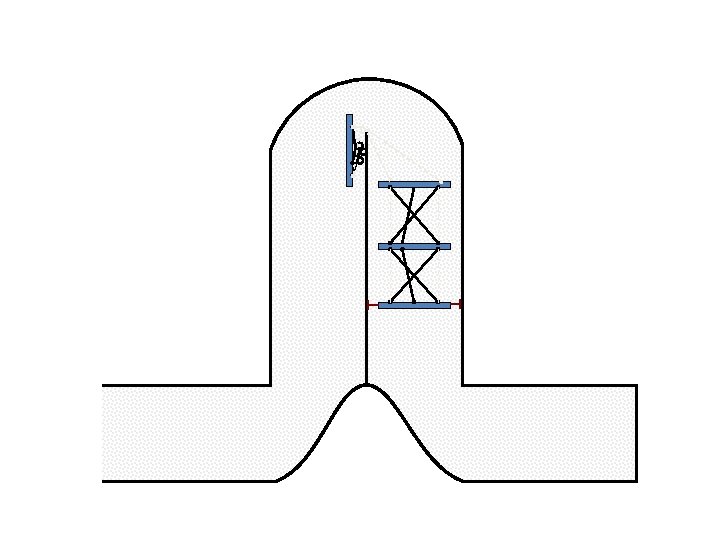
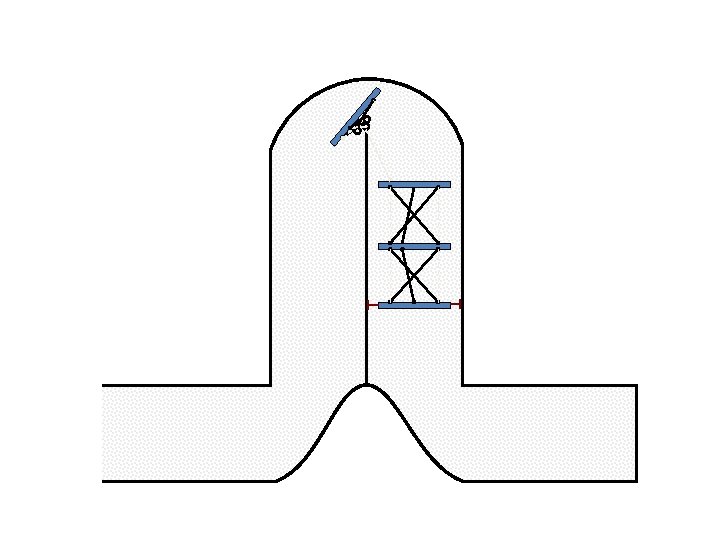
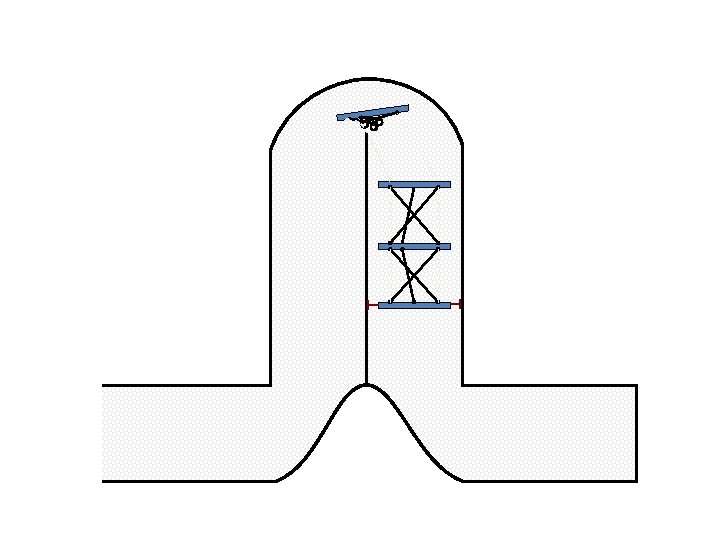
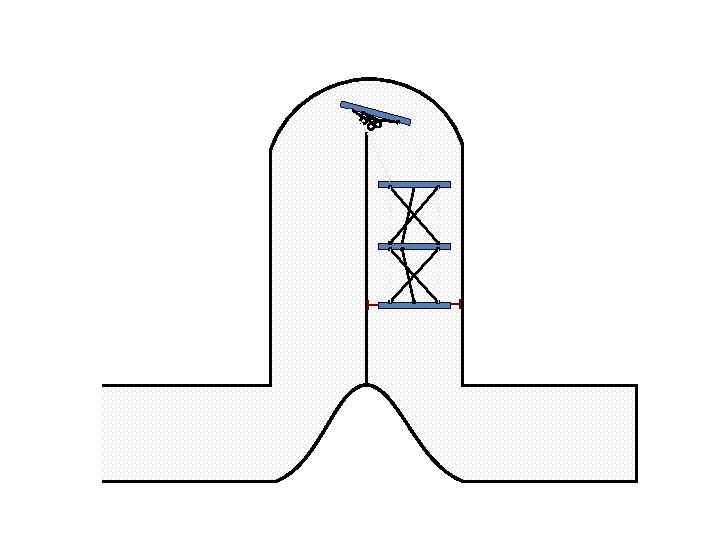
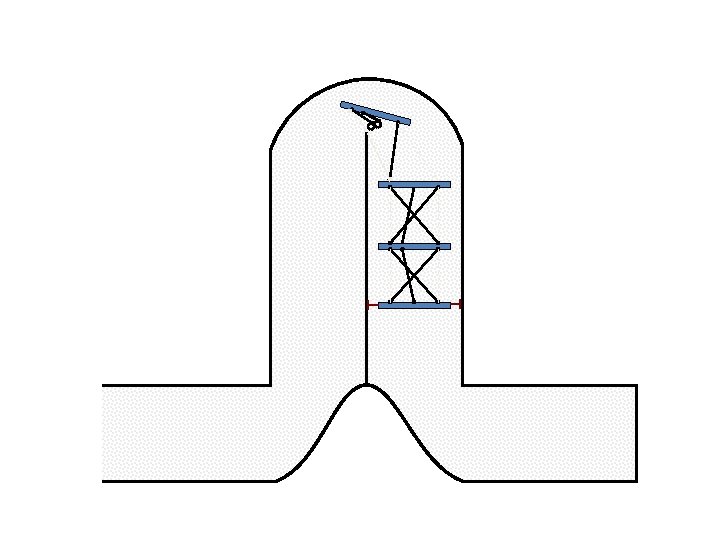
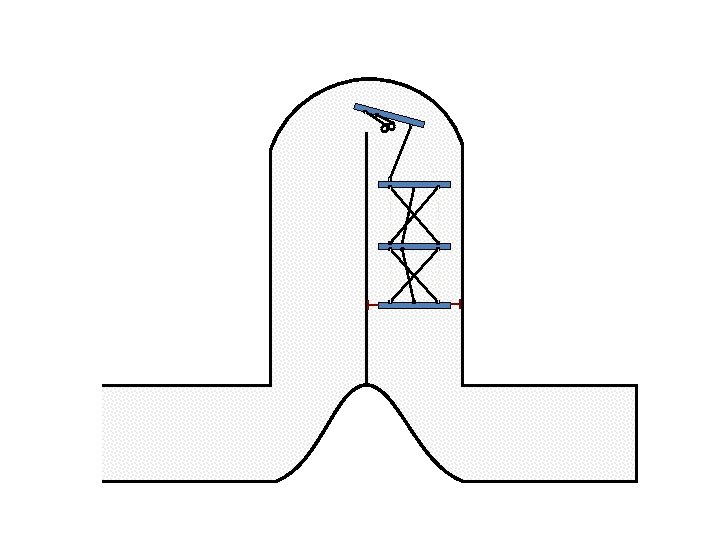
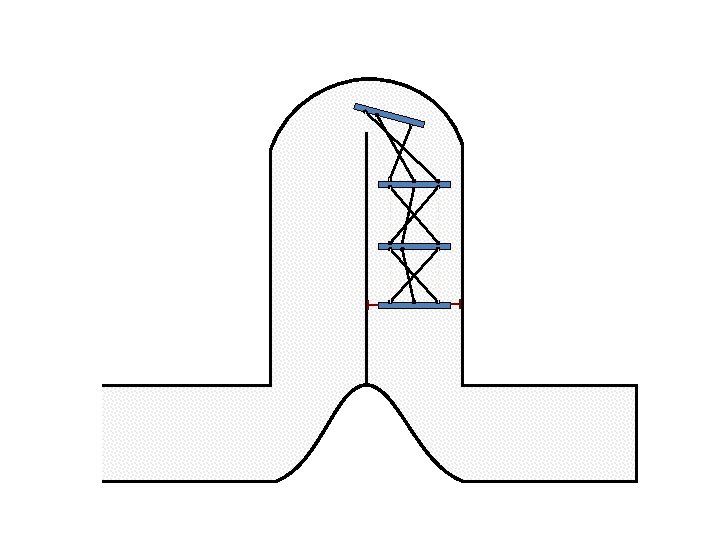
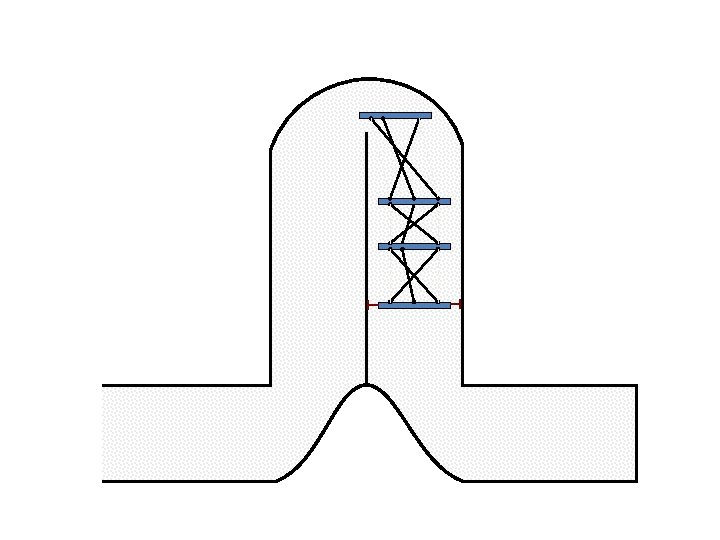
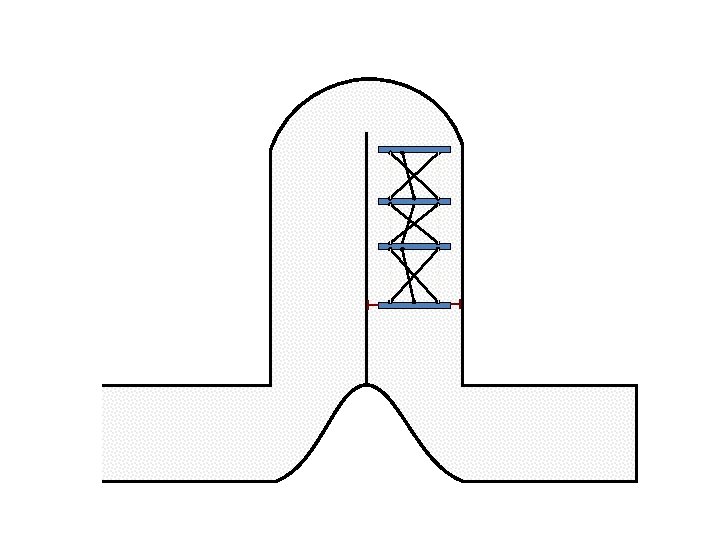
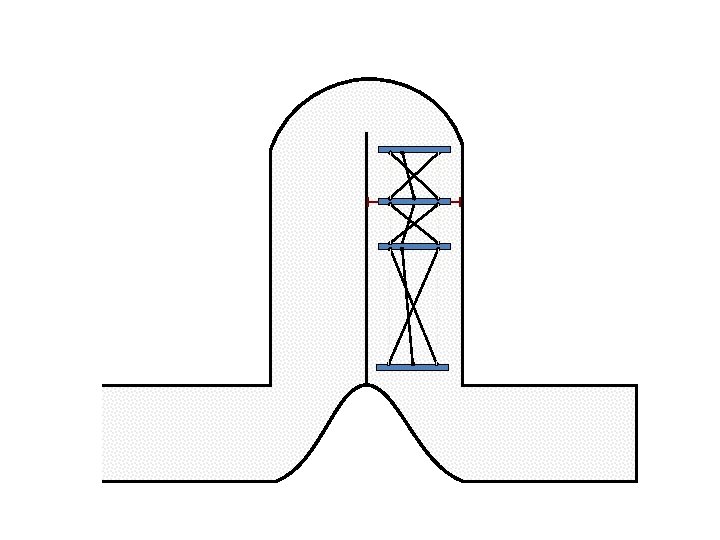
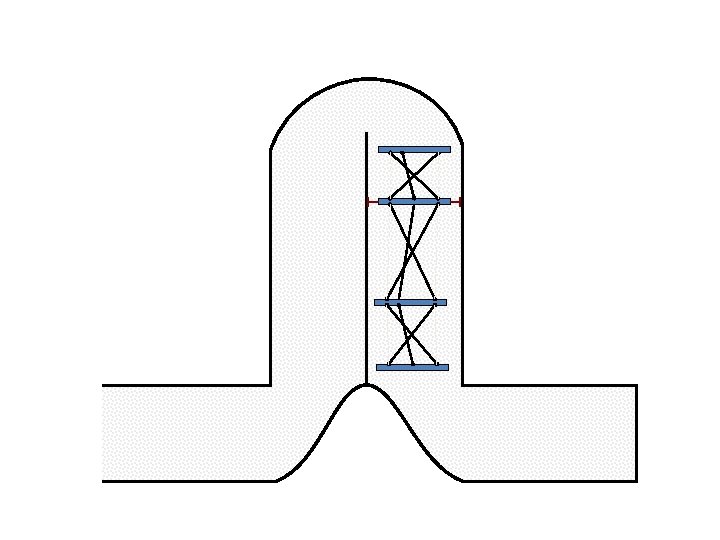
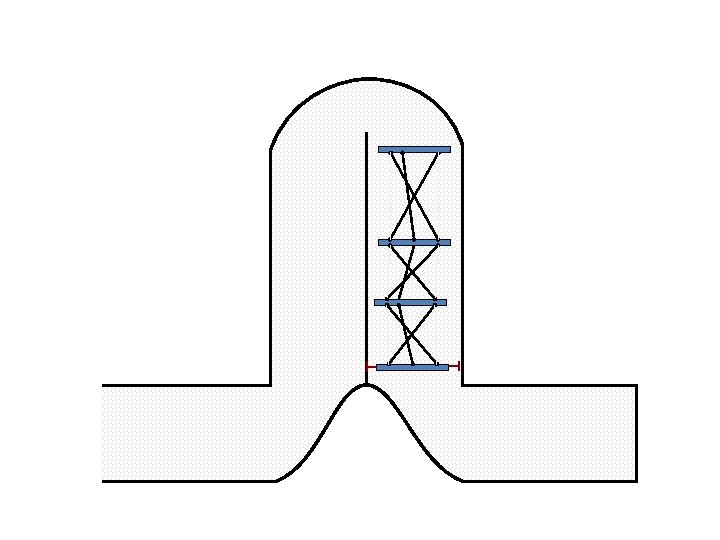
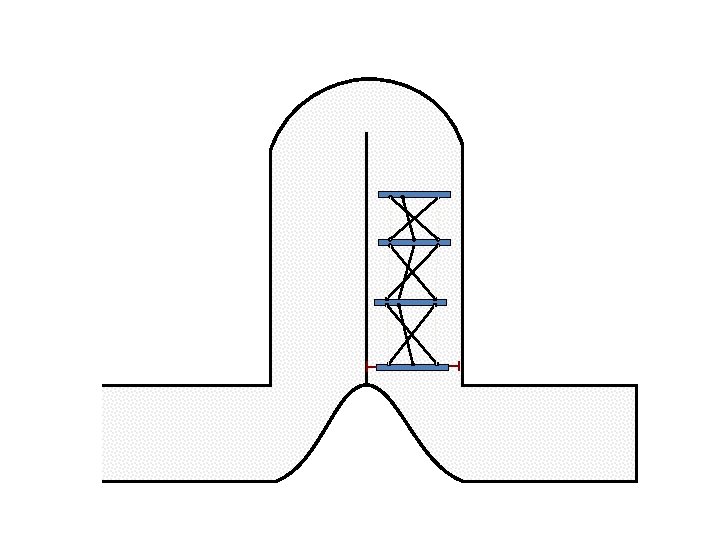
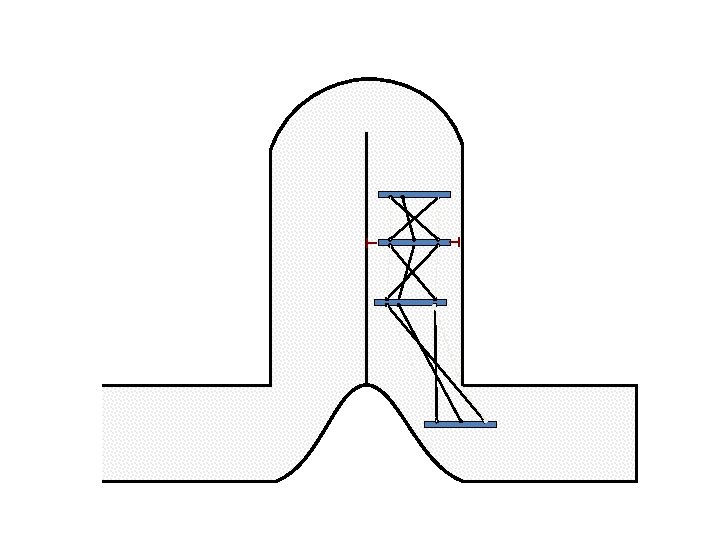
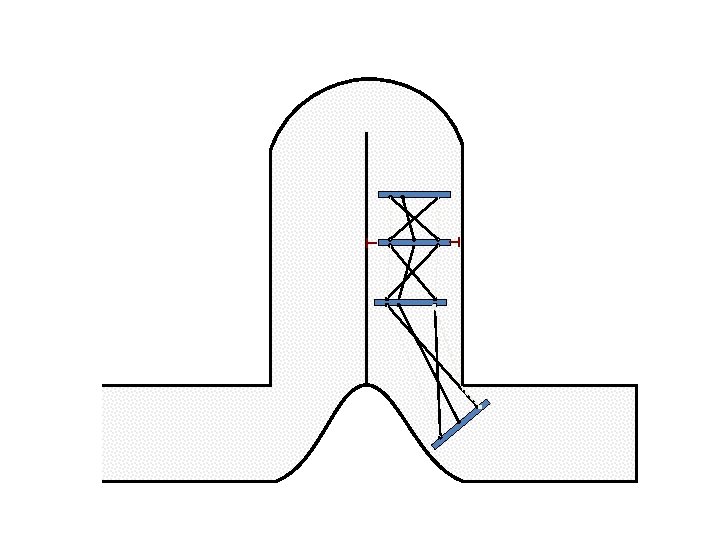
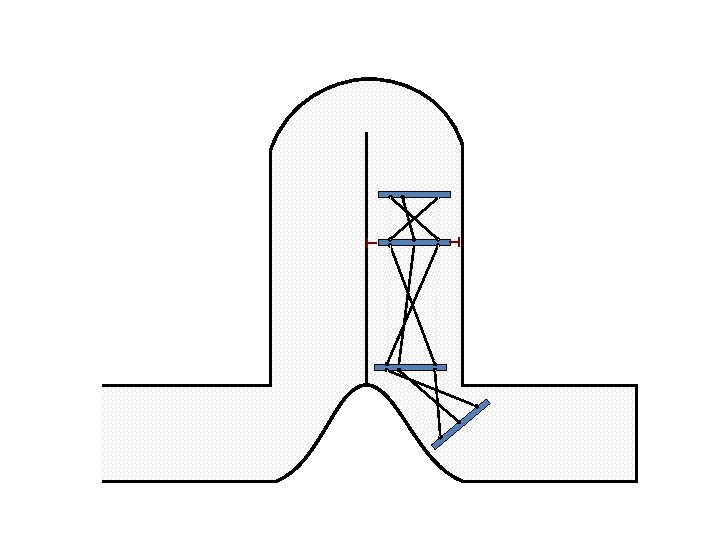
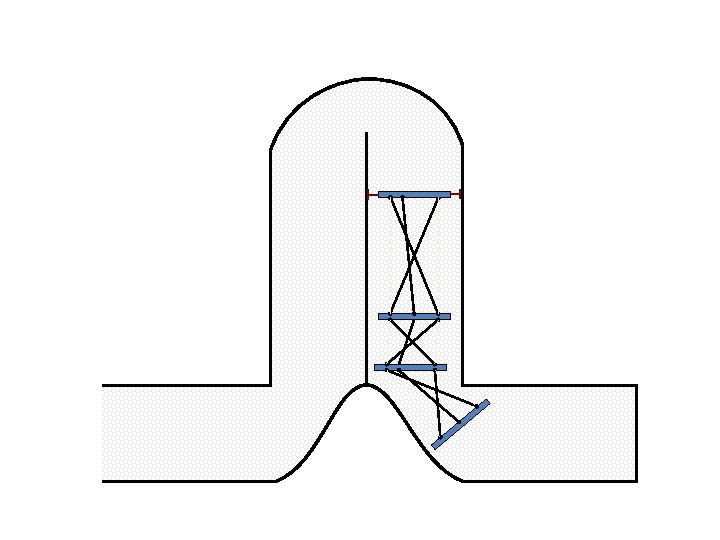
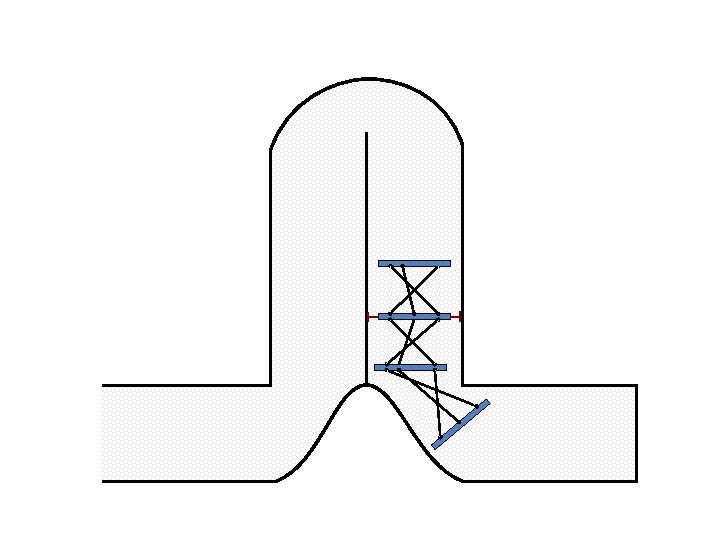
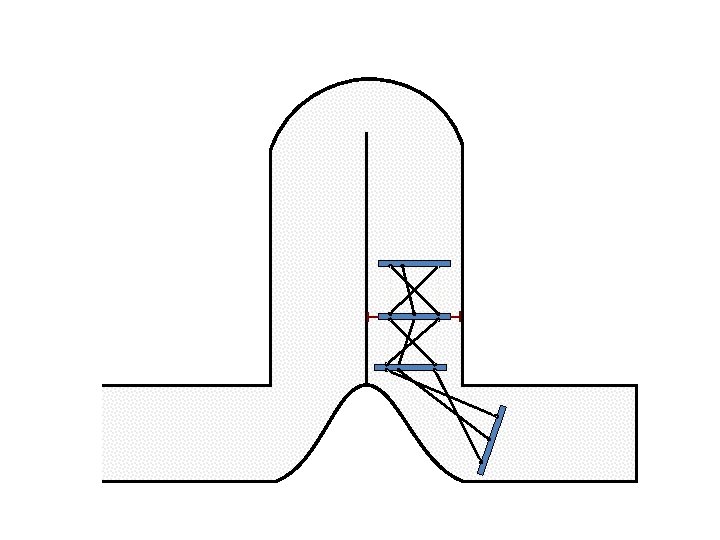
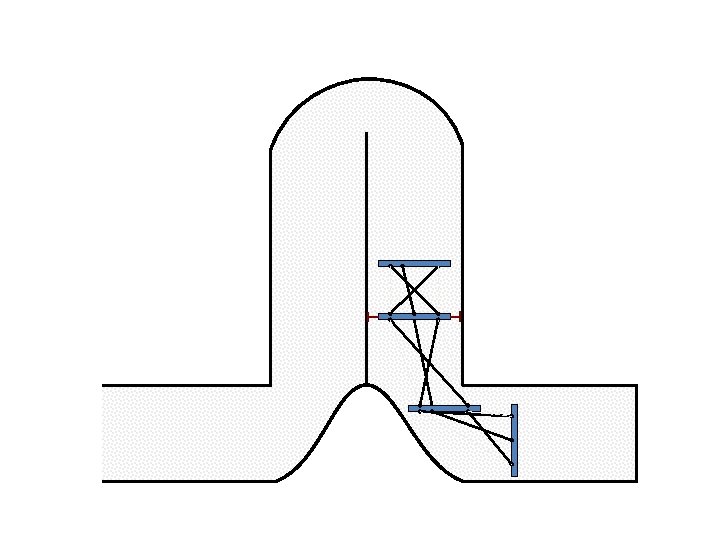
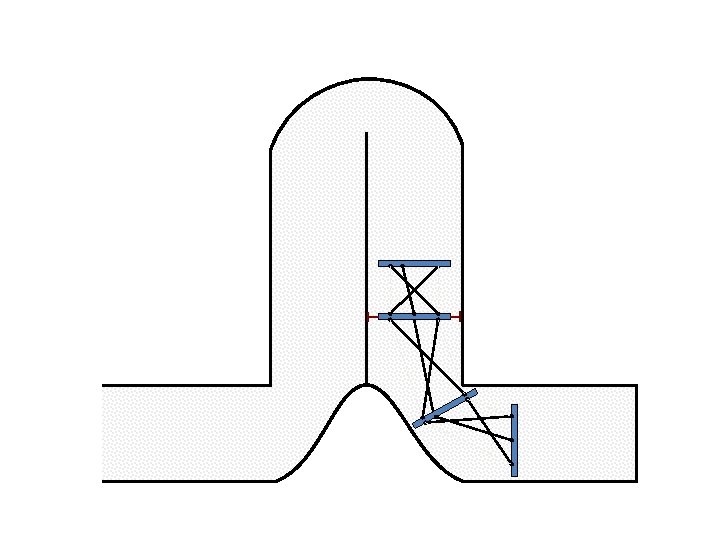
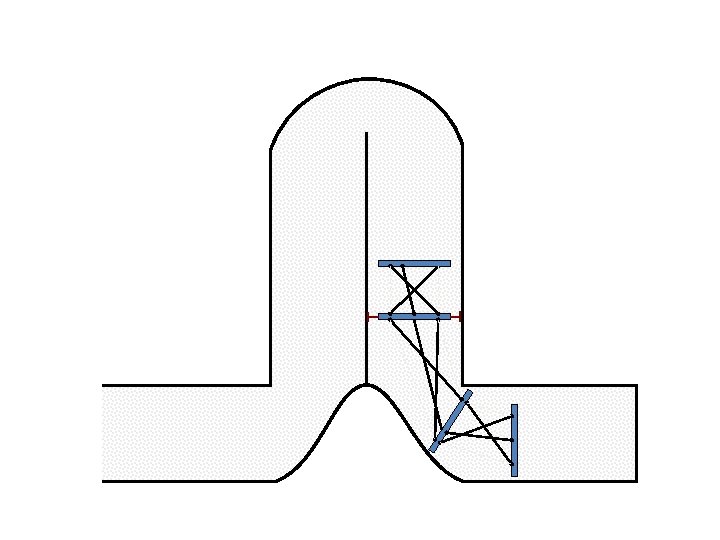
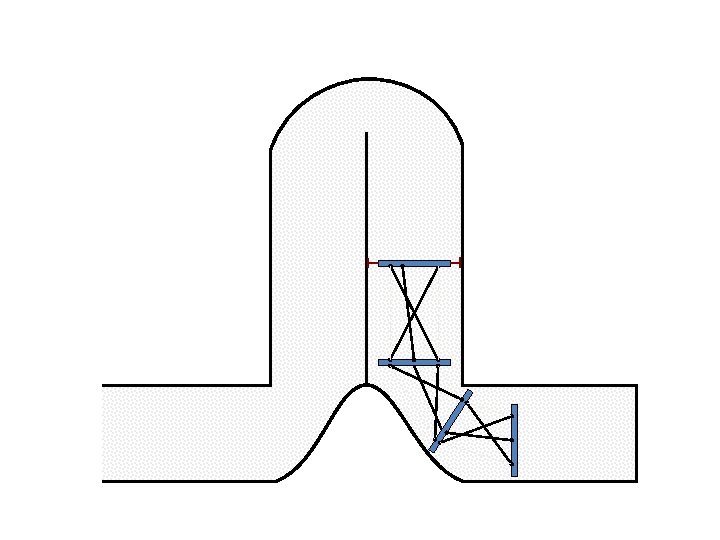
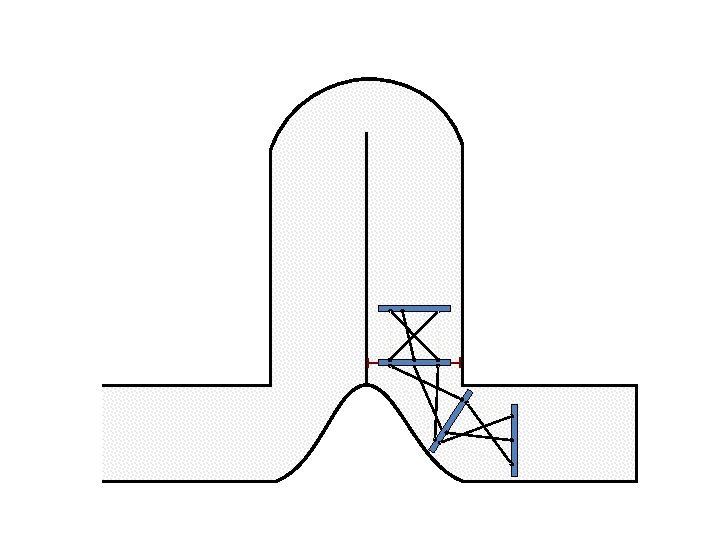
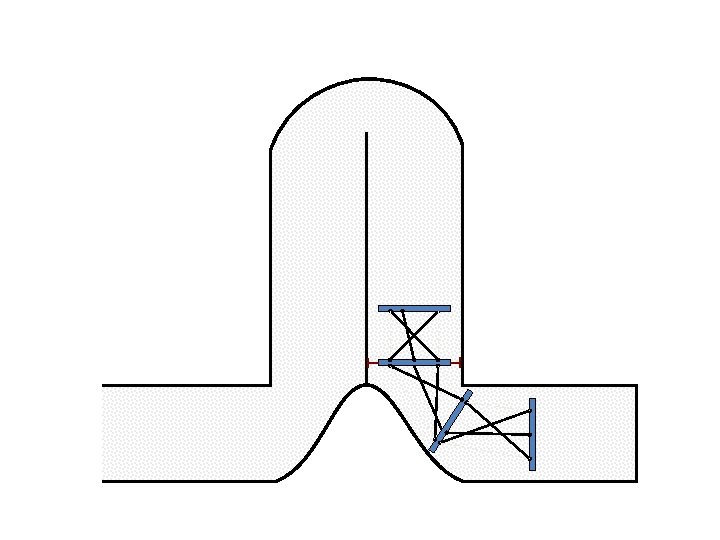
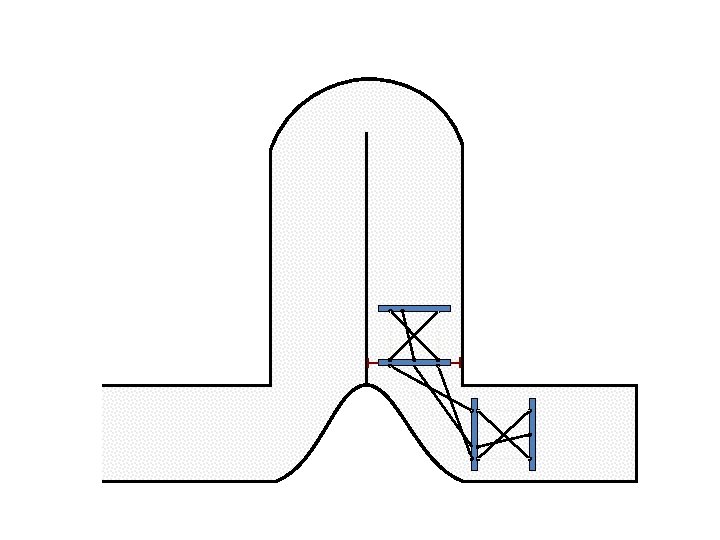
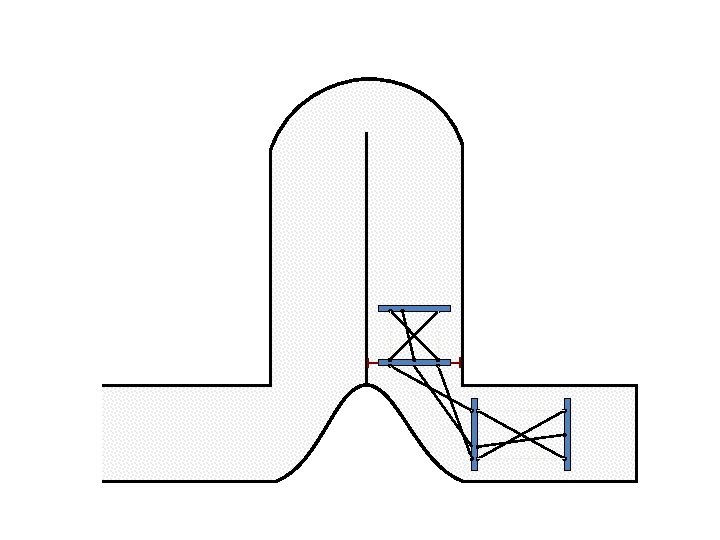
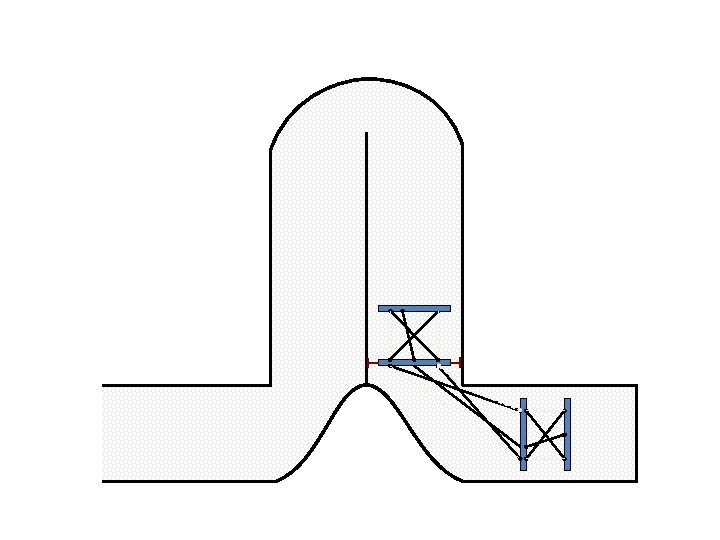
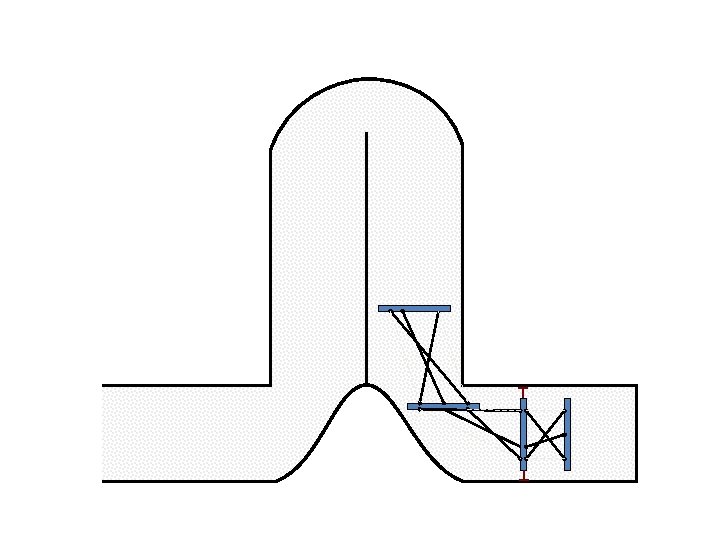
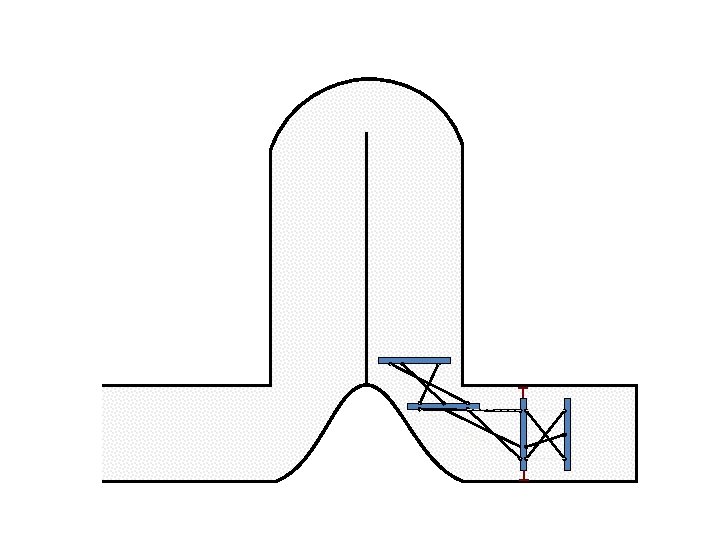
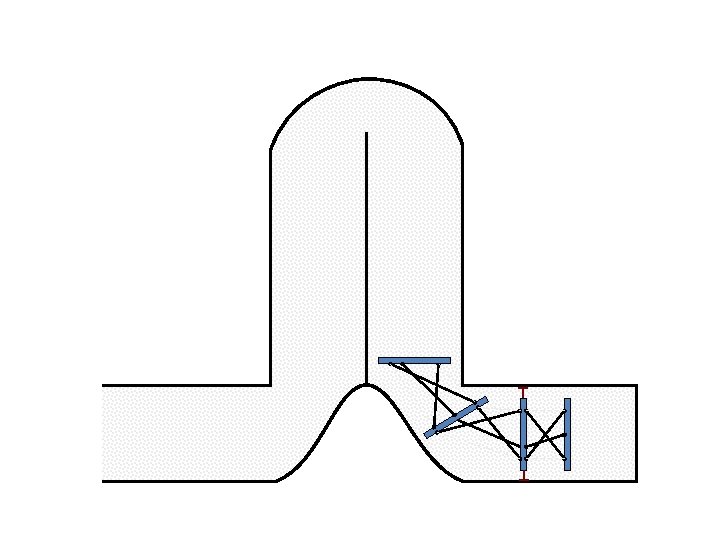
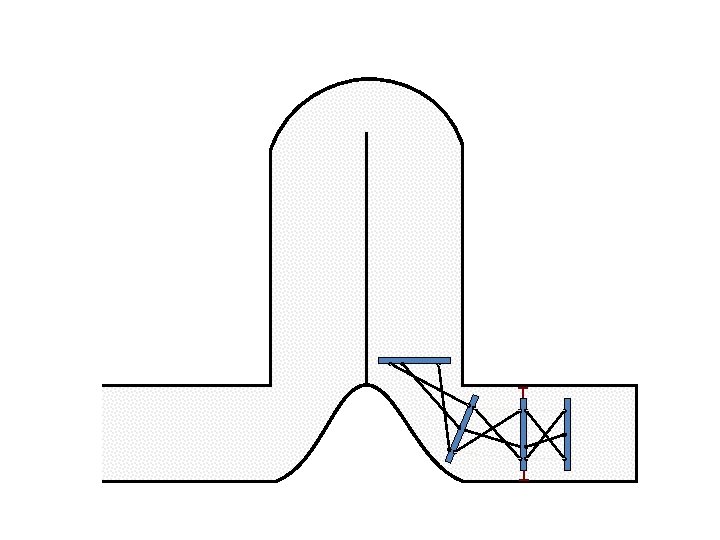
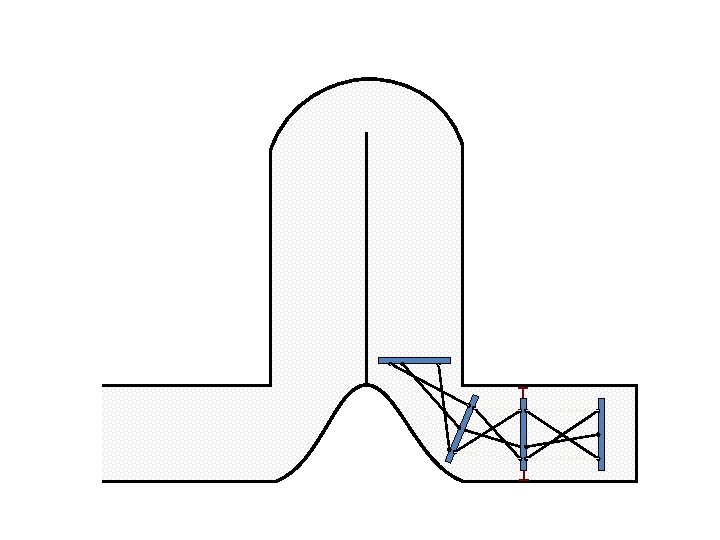
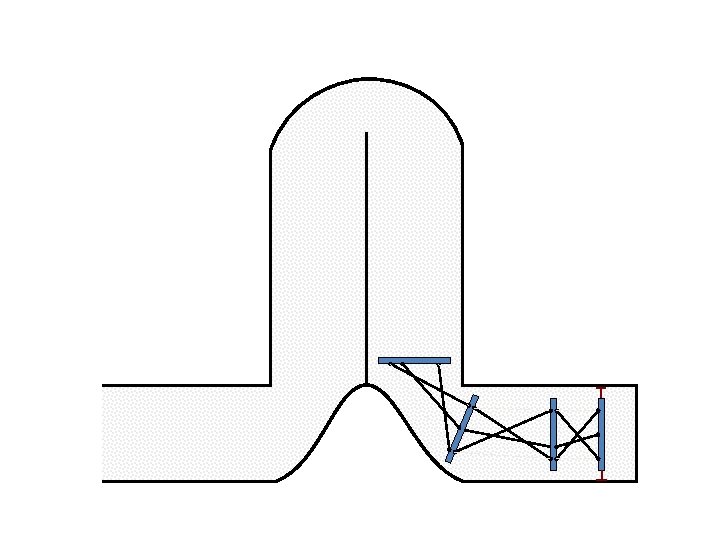
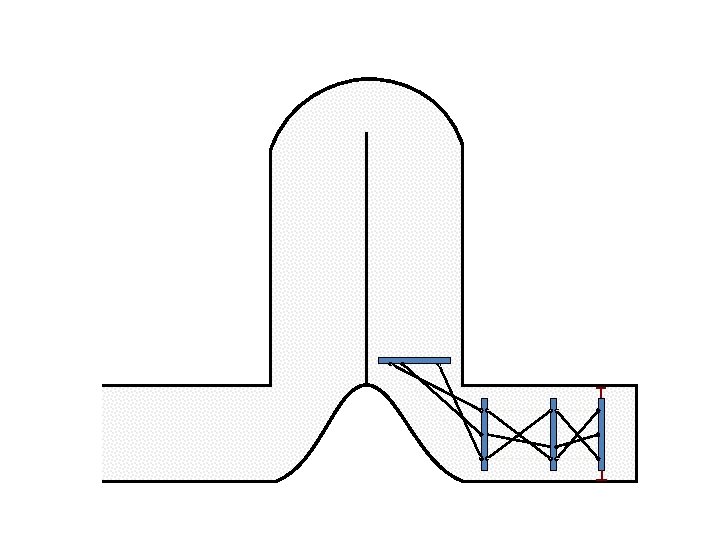
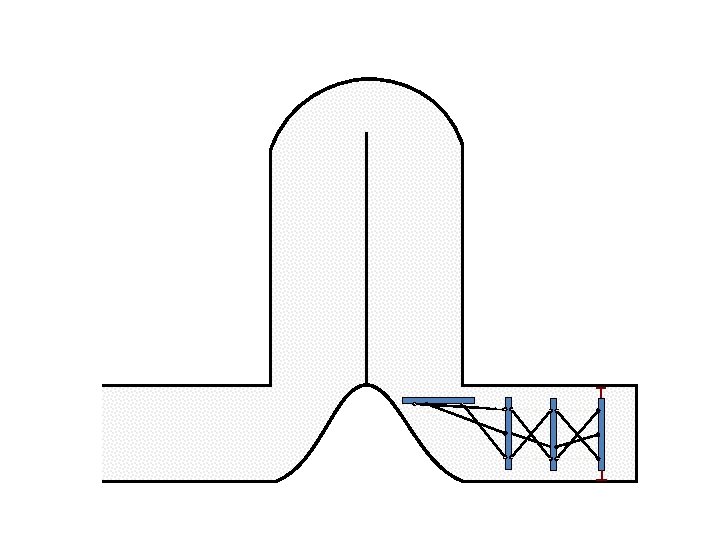
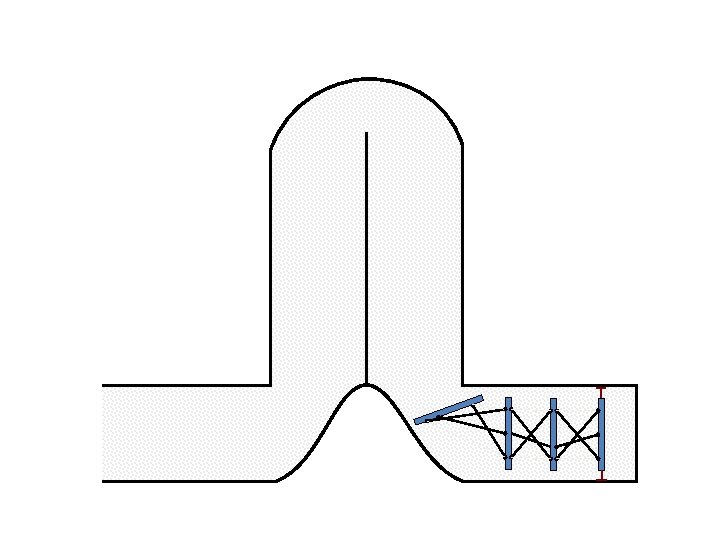
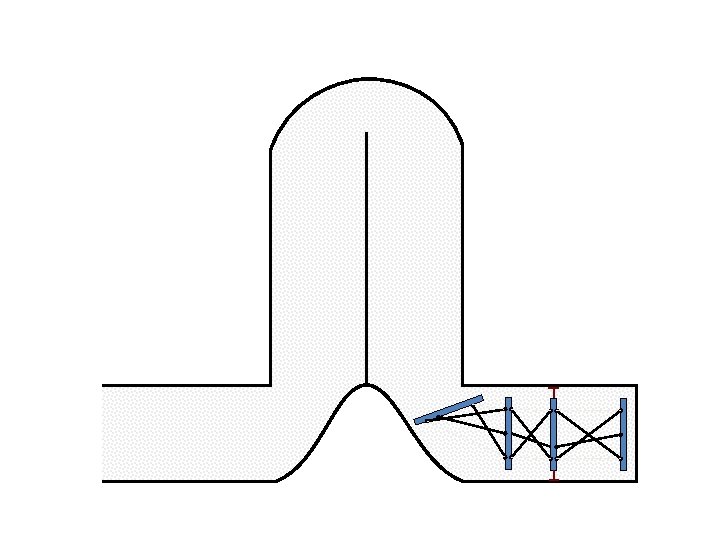
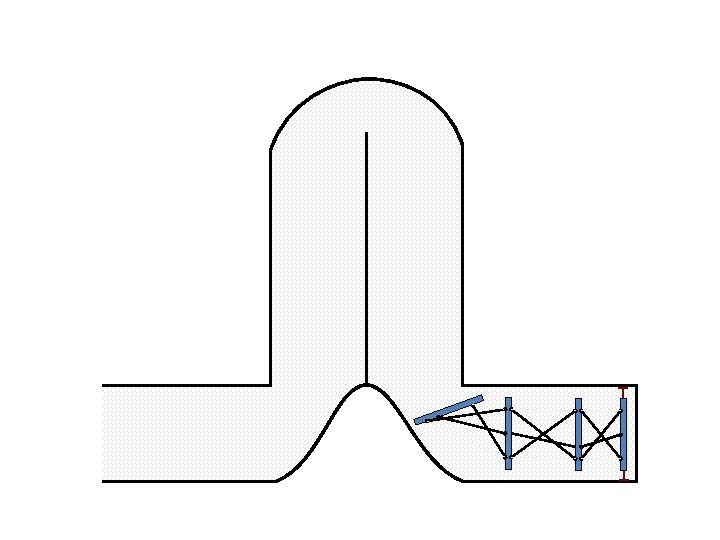
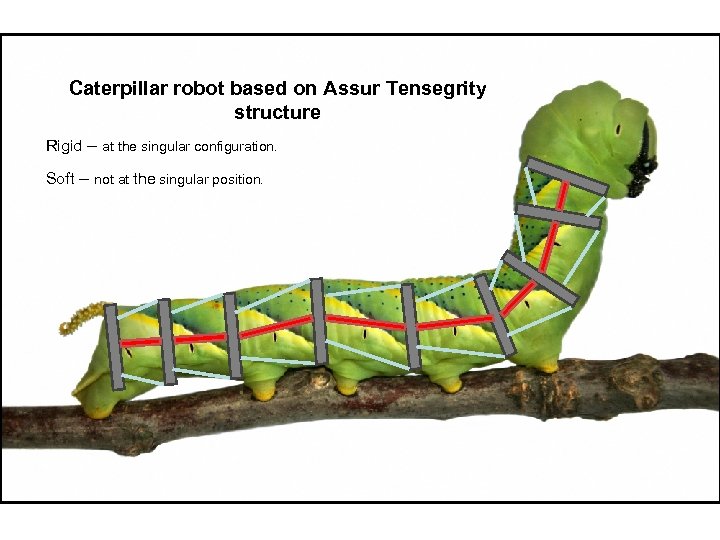Caterpillar robot based on Assur Tensegrity structure Rigid – at the singular configuration. Soft – not at the singular position.