ПРОЦЕДУРЫ И ФУНКЦИИ Процедура Procedure имя

ПРОЦЕДУРЫ И ФУНКЦИИ Процедура: Procedure < имя > ( p 1, p 2, . . . pn ) ; < раздел описаний > begin < раздел операторов > end ; Оператор вызова процедуры: <имя >( f 1, f 2, . . . fn ); 1

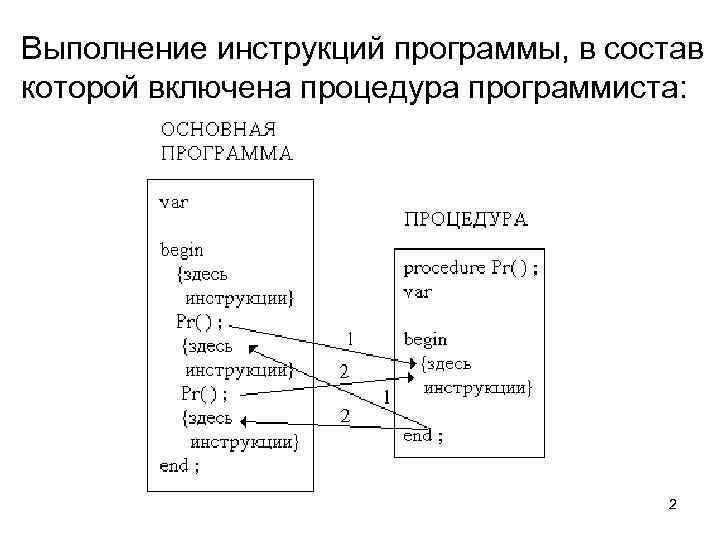Выполнение инструкций программы, в состав которой включена процедура программиста: 2

Программа: Program Example_P ; VAR i : Integer ; { процедура программиста } Procedure Line(n: integer; c: char) ; var i: integer ; begin for i: =1 to n do write(c) ; writeln ; end ; 3

Программа (продолжение): BEGIN { Основная программа } writeln('Таблица квадратных корней') line(15, '=') writeln('Число Корень') ; line(15, '=') ; for i: =1 to 5 do begin writeln(i: 5, ' ', sqrt(i): 6: 3) ; line(15, '-') end END. 4

Результат работы программы: 5

Пример: Составить программу, которая обеспечивает ввод вектора, произвольной размерности не выше 10 и его вывод на экран. Исходные данные: X=(6. 3, 7. 2, -3. 8, -9. 4, 7. 3, 0. 4) Y=(5. 8, -2. 4, 7. 1, -3. 6) 6

Программа: program Vvod_Exit; Const Nmax=10; Type Vector=array[1. . Nmax] of real; VAR x, y: Vector; {****Процедура ввода вектора****} Procedure Inp_vect(Var a: Vector; N: Integer); Var k: integer; Begin For k: =1 to N do Read(a[k]); End; 7

Программа (продолжение) {****Процедура вывода вектора****} Procedure Exit_vect(Var a: Vector; N: Integer); Var k: integer; Begin For k: =1 to N do Write(a[k]: 6: 2, ' '); writeln; End; 8

Программа (окончание) {****Основная программа****} BEGIN Write. Ln(‘Введите вектор x'); Inp_vect(x, 6); Write. Ln(‘Введите вектор y'); Inp_vect(y, 4); Write. Ln(‘Вектор x'); Exit_vect(x, 6); Write. Ln(‘Вектор y'); Exit_vect(y, 4); END. 9

Результат работы программы: Вектор x 6. 30 7. 20 -3. 80 -9. 40 7. 30 0. 40 Вектор y 5. 80 -2. 40 7. 10 -3. 60 10

Функции Function < имя > ( p 1, p 2, . . . , pn ) : <типвозвращаемого результата>; < раздел описаний > begin <раздел операторов> end ; Оператор вызова функции: < имя > ( f 1, f 2, . . . fn ); 11

Составить программу, которая вычисляет площадь двух треугольников ABC и DEF по формуле Герона. Исходные данные: Стороны треугольника ABC равны 3, 4 и 5. Стороны треугольника DEF равны 6, 9 и 11. Формула Герона: где - полупериметр a, b, c – стороны треугольника. 12

Программа: Program Example_F ; VAR A, B, C: Real ; { стороны треугольника ABC } D, E, F: Real ; { стороны треугольника DEF } Sq 1: Real ; {площадь треугольника ABC } Sq 2: Real ; {площадь треугольника DEF } { функция программиста } { Вычисление площади треугольника по формуле Герона } Function Sq. Geron(a, b, c : real) : real ; var p: real ; begin p: =(a+b+c)/2; Sq. Geron: =sqrt(p*(p-a)*(p-b)*(p-c)) end; 13

Программа (продолжение): { Основная программа } BEGIN writeln('Введите значения сторон треугольника ABC'); readln(A, B, C) ; writeln('Введите значения сторон треугольника DEF'); readln(D, E, F) ; Sq 1: =Sq. Geron(A, B, C); Sq 2: =Sq. Geron(D, E, F); writeln('Площадь треугольника ABC =', Sq 1: 6: 3) ; writeln('Площадь треугольника DEF =', Sq 2: 6: 3) ; END. 14

Результат работы программы: Площадь треугольника ABC = 6. 000 Площадь треугольника DEF =26. 981 15

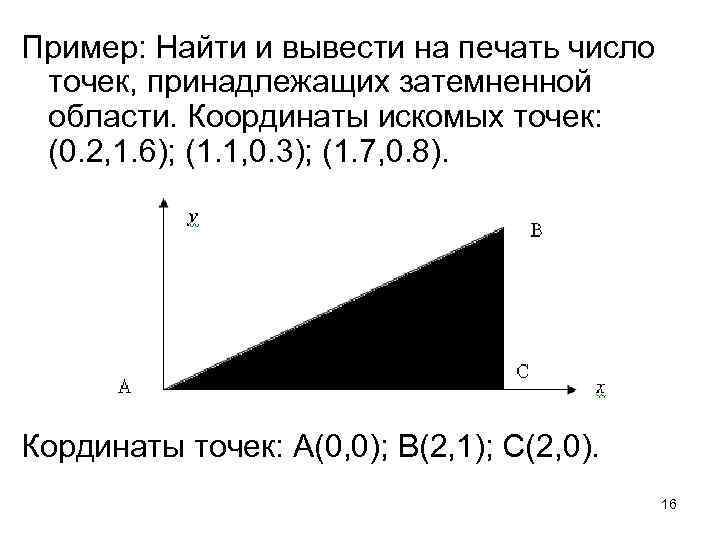Пример: Найти и вывести на печать число точек, принадлежащих затемненной области. Координаты искомых точек: (0. 2, 1. 6); (1. 1, 0. 3); (1. 7, 0. 8). Кординаты точек: A(0, 0); B(2, 1); C(2, 0). 16

Расчеты: Уравнение прямой AC: y=0. Уравнение прямой BC: x=2. Найдем уравнение прямой AB: В общем виде y = kx + m В точке A имеем 0=k*0+m. Отсюда m=0. В точке B имеем 1=k*2+m. Отсюда k=1/2=0. 5 Значит уравнение прямой AB: y = 0. 5 * x. 17

Program Region; Var x, y : real ; k, k 1, k 2, k 3 : integer ; Function Tochka(x, y : real) : integer ; begin if ((x <= 2) and (y >= 0) and (y <= 0. 5 * x)) Then Tochka : = 1 Else Tochka : = 0 ; end; BEGIN K 1 : =Tochka(0. 2, 1. 6); K 2 : =Tochka(1. 1, 0. 3); K 3 : =Tochka(1. 7, 0. 8); K : =k 1 + k 2 + k 3; Write. Ln('число точек, принадлежащих затемненной области k=', k: 1); END. 18

Параметры-процедуры и параметры-функции Формат процедурного типа: Type < имя-типа >=Procedure( p 1, p 2, . . . , pn); или Type < имя-типа >=Function( p 1, p 2, . . . , pn ): < тип результата >; 19

Директива компилятора Far - адресация Near -адресация {$F+} {$F-} 20

Пример. Программа, печатающая таблицы сложения и умножения двух целых чисел в заданном диапазоне. Program Example ; TYPE Func = function(X, Y : Integer) : Integer ; {$F+} function Add(X, Y : Integer) : Integer ; begin Add : = X + Y end ; function Multiply(X, Y : Integer) : Integer ; begin Multiply : = X * Y end ; {$F-} 21

Программа (продолжение): { процедура печати таблицы } Procedure Print. Table(A, B : Integer; Operation : Func) ; var i, j : integer ; begin for i: =1 to A do begin for J: =1 to B do write(Operation(i, j): 5) ; writeln end ; writeln end ; BEGIN { основная программа } Print. Table(10, Add) ; Print. Table(10, Multiply) ; 22 END.

Задача 1. Вычислить интегралы и по формуле трапеций с заданной точностью. a и b – нижний и верхний пределы интегрирования n – начальное значение разбиения промежутка интегрирования. Вычисление интеграла оформить в виде функции 23

Программа: {$F+} {Опция компилятора для обеспечения дальнего вызова} Program Integ; Type f. User=function(x: real): real ; Var Int 1, Int 2 : real; {***Первая подинтегральная функция****} function f 1(t: real): real; begin f 1: =(t*t*t+7*t*t+1)/(2*t+3) end; {***Вторая подинтегральная функция****} function f 2(t: real): real; begin f 2: =t*t*exp(t) end; 24

Программа (продолжение): {Вычисление интеграла с заданной точностью} function Integral(a, b: real; n: integer; eps: real; f: f. User): real; Var s, sold, h, delta, x : r eal; I : integer; Begin sold: =0; Repeat s: =(f(a)+f(b))/2; h: =(b-a)/n; x: =a; for i: =1 to n-1 do begin x: =x+h; s: =S+f(x); end; 25

Программа (окончание): s: =s*h; delta: =abs(sold-s); sold: =s; n: =2*n; until delta < eps ; Integral: =s; End; BEGIN Int 1: =Integral(0. 1, 2. 6, 4, 0. 001, f 1); Write. Ln('Значение первого интеграла Int 1=', int 1: 8: 5); Int 2: =Integral(-0. 5, 3. 0, 4, 0. 001, f 2); Write. Ln('Значение второго интеграла Int 2=', int 2: 8: 5); END. 26

Результат работы программы: Значение первого интеграла Int 1= 8. 19089 Значение второго интеграла Int 2=98. 45675 27