Проблемы дружественных чисел


Проблемы дружественных чисел

План: 1) Понятие «дружественные числа» 2) Из истории дружественных чисел 3) Таблица дружественных пар 4) Проблемы дружественных чисел

О понятии «дружественные числа» • Понятие «дружественные числа» являются обобщением понятия «совершенные числа» . • Совершенными называются числа, равные сумме всех своих правильных делителей (т. е. всех делителей, кроме делителя, равного самому числу). Рассмотрим, как получены «дружественные числа» .

О понятии «дружественные числа» Возьмем любое число и просуммируем его делители для получения второго числа. Затем просуммируем делители второго числа … и так далее в надежде, что, в конце концов, можно прийти к исходному числу. Если исходное число получается на первом шаге, значит цепочка имеет лишь одно звено, а само число – совершенное.

О понятии «дружественные числа» Если исходное число получается на втором шаге (при двухзвенной цепочке) два числа образуют дружественную пару: сумма делителей одного из чисел равна другому числу. Наименьшие дружественные числа, образующие пару, равны 220 и 284. 1+2+4+5+10+11+20+22+44+55+110=284 1+2+4+71+142=220
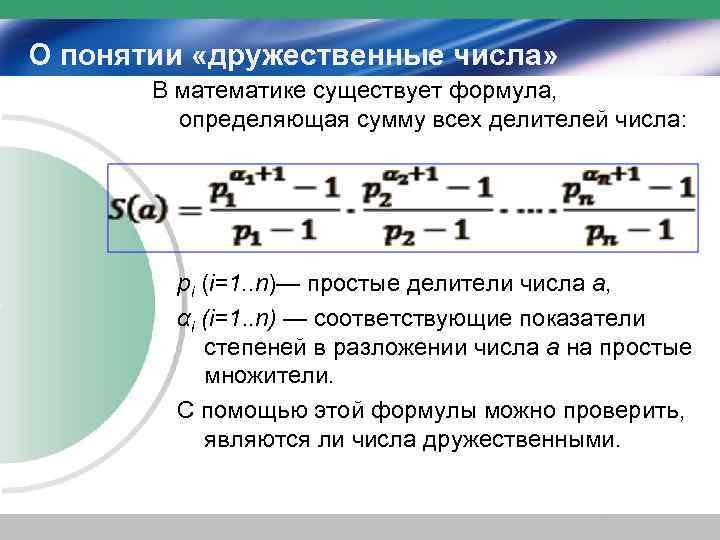
О понятии «дружественные числа» В математике существует формула, определяющая сумму всех делителей числа: pi (i=1. . n)— простые делители числа a, αi (i=1. . n) — соответствующие показатели степеней в разложении числа a на простые множители. С помощью этой формулы можно проверить, являются ли числа дружественными.

О понятии «дружественные числа» Для этого используем как необходимое и достаточное условие того, что два числа a и b дружественные, систему: Для пары 220 и 284:

Из истории дружественных чисел • Наименьшие дружественные числа, образующие пару (220 и 284) были известны еще Пифагору. Пифагор (ок 570 - ок 500 до н. э. ) • В 1636 году Пьер Ферма нашел другую дружественную пару чисел: 17 296 и 18 416. П. Ферма (1601 – 1665)

Из истории дружественных чисел • Пьер Ферма и Рене Декарт независимо друг от друга дали правило образования дружественных пар. Р. Декарт (1596 - 1650) • Позже оказалось, что это правило было сформулировано еще в IX веке арабским астрономом месопотамского города Харрана – Абу-л-Хасаном Сабитом ибн Кора ибн Марван ас Саби ал- Харрани (ок. 830 – 901 гг. )

Из истории дружественных чисел • Теорема Сабита: • Если числа p, q, r вида простые, то числа A и B, где составляют дружественную пару.

Из истории дружественных чисел Эта формула даёт пары для n=2 — пара чисел Пифагора 220 и 284, n=4 — пара чисел Ибн аль-Банны и Ферма 17296 и 18416, n=7 — пара чисел Декарта 9 363 584 и 9 437 056 (1638 г. ) Но больше никакие пары дружественных чисел для n < 20000 (как и многие другие) не могут быть по ней получены.

Из истории дружественных чисел • Известен также способ нахождения дружественных пар, предложенный Вальтером Боро и позволяющий находить довольно большие дружественные числа: • Если для пары дружественных чисел вида A=au и B=as где s и p=u+s+1 – простые, причем a не делится на p, то при всех натуральных n, при которых q 1=(u+1)pn+1 -1 и q 2=(u+1)(s+1)pn-1 – простые, числа B 1=Apnq 1 и B 2=apnq 2 образуют дружественную пару.

Из истории дружественных чисел • Открытие третьей пары дружественных чисел 9 363 584 и 9 437 056 в 1638 году принадлежит Декарту. • В XVIII веке Эйлер опубликовал список 64 дружественных пар, однако, как показала дальнейшая проверка, в двух случаях он ошибся. Л. Эйлер (1707 – 1783)

Из истории дружественных чисел • В 1830 году Адриен Мари Лежандр нашел еще одну дружественную пару. • В 1867 году 16 -летний итальянский юноша Б. И. Паганини удивил математический мир, объявив, что числа 1184 и 1210 – дружественные. А. М. Лежандр (1752 – 1833) Это была вторая по величине пара, которую все проглядели. И хотя, возможно, Паганини нашел эту пару методом проб и ошибок, имя его навсегда вошло в историю теории чисел.

Из истории дружественных чисел • Пару чисел 220 и 284 стали считать символом любви и дружбы: - в средние века имели хождение талисманы с выгравированными на них числами 220 и 284, якобы способствующими укреплению любви; - некий арабский нумеролог сообщает об обычае вырезать числа 220 и 284 на плодах, которые должны были съесть влюбленные; - первые теологи отмечали, что в Книге Бытия Иаков отдает в подарок своему брату Исаву 220 животных, что по их мнению свидетельствует о любви Иакова к Исаву.

Из истории дружественных чисел • На ноябрь 2006 года стало известно 11 446 960 пар дружественных чисел. • Все они состоят из двух четных или двух нечетных чисел.
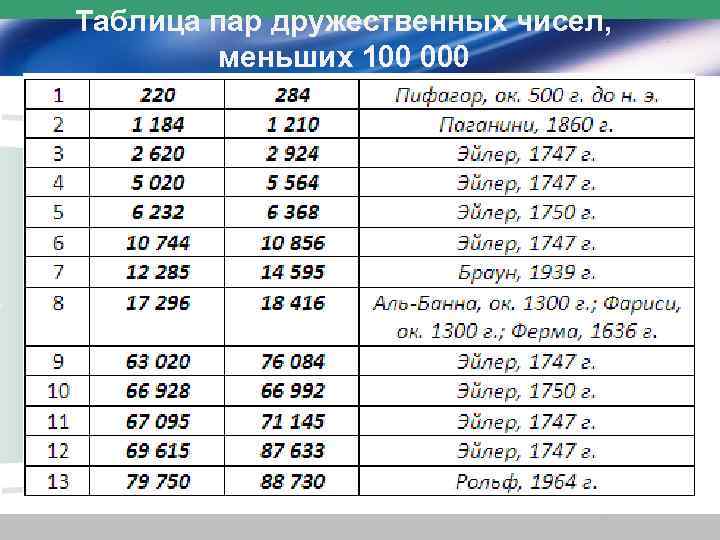
Таблица пар дружественных чисел, меньших 100 000

Проблемы дружественных чисел • Все известные дружественные пары состоят либо из двух четных чисел, либо (что гораздо реже) из двух нечетных. • Но никто не доказал, что не существует дружественной смешанной пары. • Брэтли и Мак-Кэй выдвинул гипотезу, что все нечетные дружественные числа кратны 3, а сумма чисел, образующую дружественную пару, кратна 9.

Проблемы дружественных чисел • Также никто еще не предложил общей формулы для всех дружественных пар, и неизвестно, конечно или бесконечно число таких пар. • Неизвестно, существуют ли взаимно простые дружественные числа. Но, если такая пара дружественных чисел существует, их произведение должно быть больше 1067.

Проблемы дружественных чисел • В XX веке математики обобщили понятие дружественных чисел и занялись поиском дружественных рядов — замкнутых циклов из трех и более звеньев цепочки. • Например, в тройке чисел 1 945 330 728 960, 2 324 196 638 720, 2 615 631 953 920 делители первого числа в сумме дают второе число, делители второго — третье число, а делители третьего — первое.

Проблемы дружественных чисел • В 1918 году французский математик П. Пуле нашел цепочку из пяти звеньев (12 496, 14 288, 15 472, 14 536, 14 264) и поразительную цепочку из 28 звеньев (28 — совершенное число), которая начинается с числа 14 316. Это самый длинный из известных циклов.

Проблемы дружественных чисел • Вывод: Таким образом, открытыми остаются следующие проблемы дружественных чисел: 1) Существует ли смешанная дружественная пара? 2) Конечно или бесконечно число дружественных пар? 3) Существует ли формула для нахождения всех дружественных пар? 4) Верна ли гипотеза Брэтли и Мак-Кэй, что все нечетные дружественные числа кратны 3, а сумма чисел, образующую дружественную пару, кратна 9.

Список литературы • Варпаховский А. С. Тайны совершенных чисел и дружественные пары // «Квант» . – 1973 г. - № 10. – с. 71 -74. • Жуков А. Узы дружбы в мире чисел // «Кванта» . – с. 32 -33. • Мартынов Л. М. Элементы алгебры и теории чисел, 2 -е изд. – Омск: Сиб. АДИ, 2006. – 195 с. • http: //ru. wikipedia. org/wiki/Дружественные_числа • http: //dic. academic. ru/dic. nsf/ruwiki/17943

Спасибо за внимание

