2599bbc0dfc09a449d27f27d6d3663da.ppt
- Количество слайдов: 24

PROBLEMS The gear has the angular motion shown. Determine the angular velocity and angular acceleration of the slotted link BC at this instant. The pin at A is fixed to the gear. C A w=2 rad/s 2 m 0. 5 m 0. 7 m B O a=4 rad/s 2
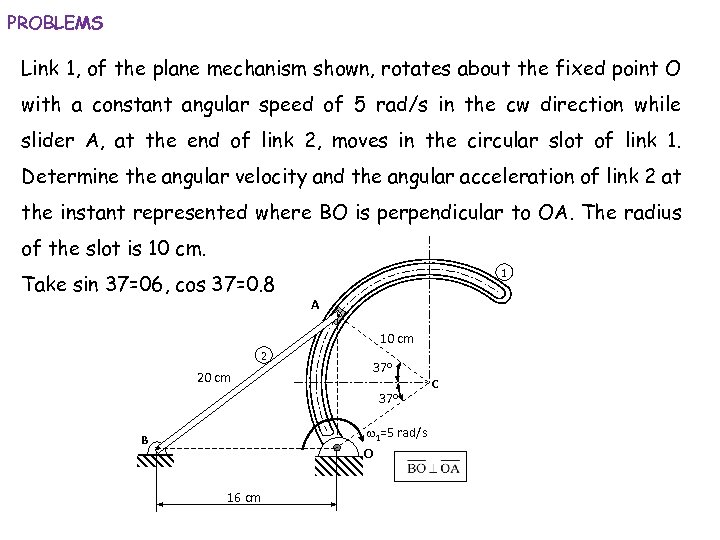
PROBLEMS Link 1, of the plane mechanism shown, rotates about the fixed point O with a constant angular speed of 5 rad/s in the cw direction while slider A, at the end of link 2, moves in the circular slot of link 1. Determine the angular velocity and the angular acceleration of link 2 at the instant represented where BO is perpendicular to OA. The radius of the slot is 10 cm. Take sin 37=06, cos 37=0. 8 1 A 10 cm 2 20 cm 37 o w 1=5 rad/s B O 16 cm C
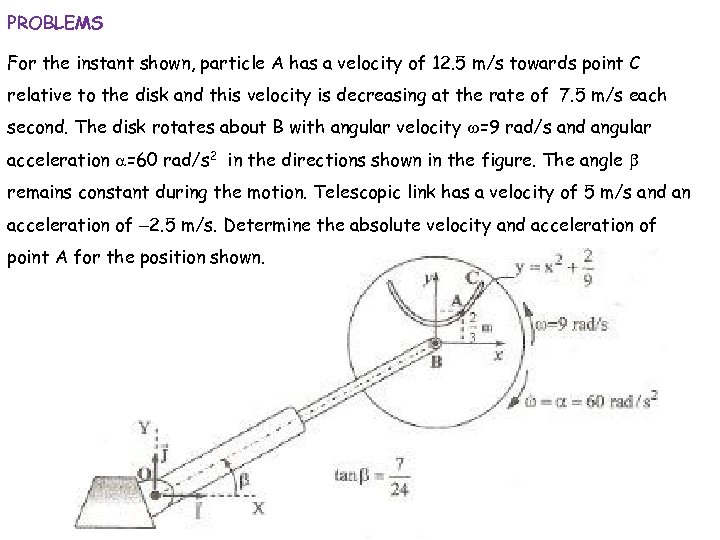
PROBLEMS For the instant shown, particle A has a velocity of 12. 5 m/s towards point C relative to the disk and this velocity is decreasing at the rate of 7. 5 m/s each second. The disk rotates about B with angular velocity w=9 rad/s and angular acceleration a=60 rad/s 2 in the directions shown in the figure. The angle b remains constant during the motion. Telescopic link has a velocity of 5 m/s and an acceleration of -2. 5 m/s. Determine the absolute velocity and acceleration of point A for the position shown.

Problem 7 Velocity Analysis v. B b 25 24 7
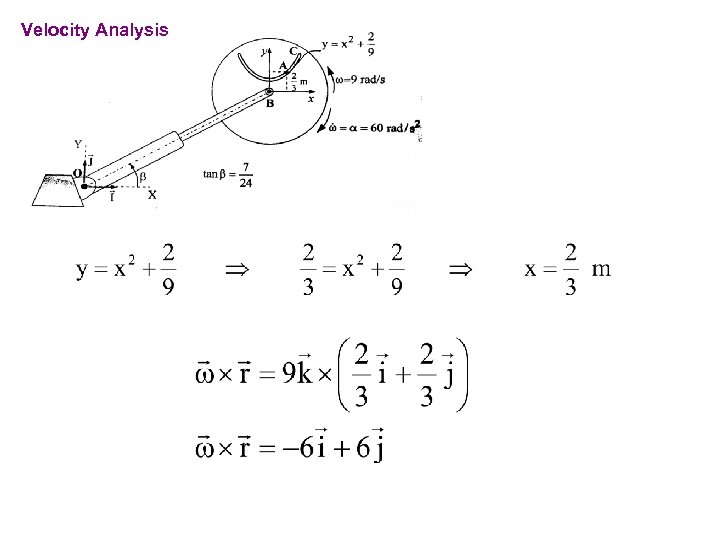
Velocity Analysis
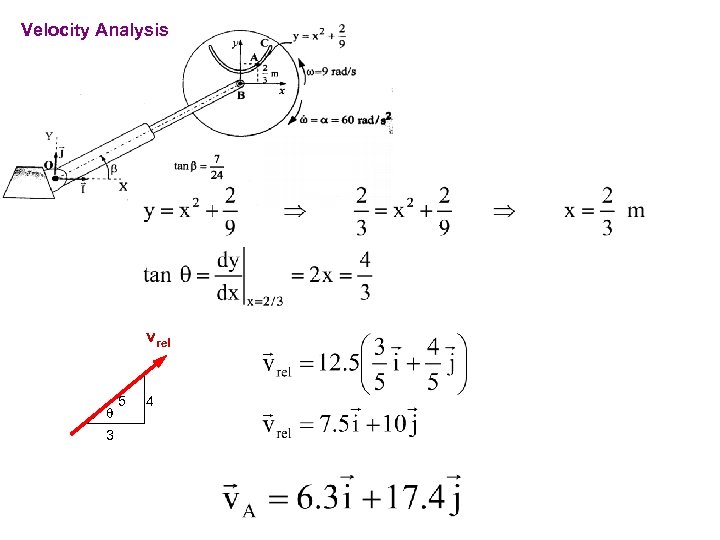
Velocity Analysis vrel q 3 5 4

Acceleration Analysis a. B b 25 24 7
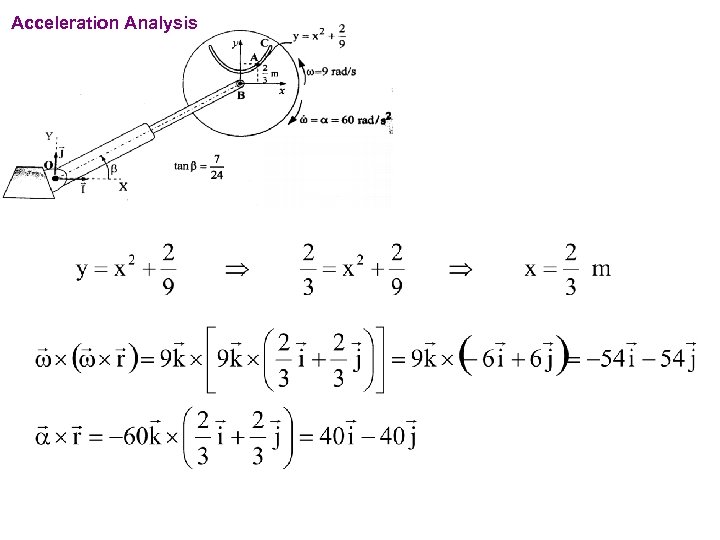
Acceleration Analysis
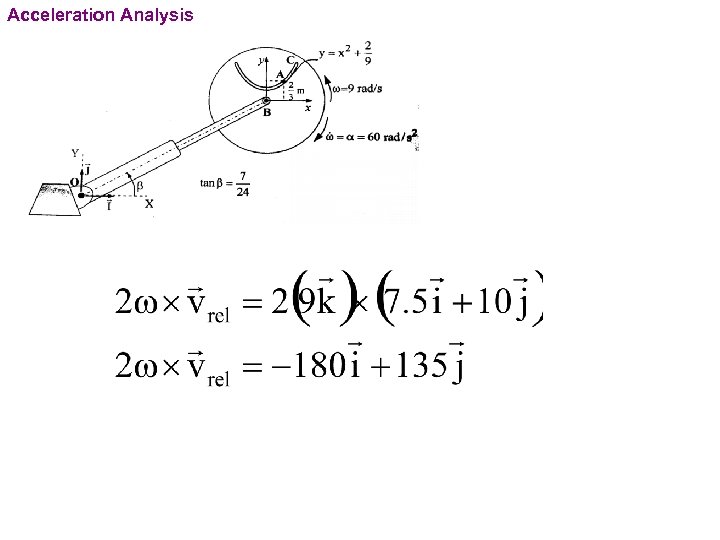
Acceleration Analysis
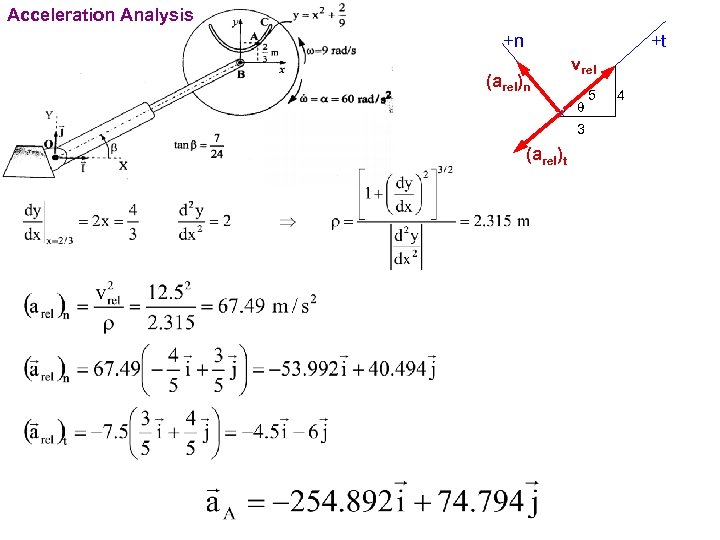
Acceleration Analysis +n +t (arel)n vrel q 3 (arel)t 5 4

PROBLEMS The pin A in the bell crank AOD is guided by the flanges of the collar B, which slides with a constant velocity v. B of 0. 9 m/s along the fixed shaft for an interval of motion. For the position q=30 o determine the acceleration of the plunger CE, whose upper end is positioned by the radial slot in the bell crank. .
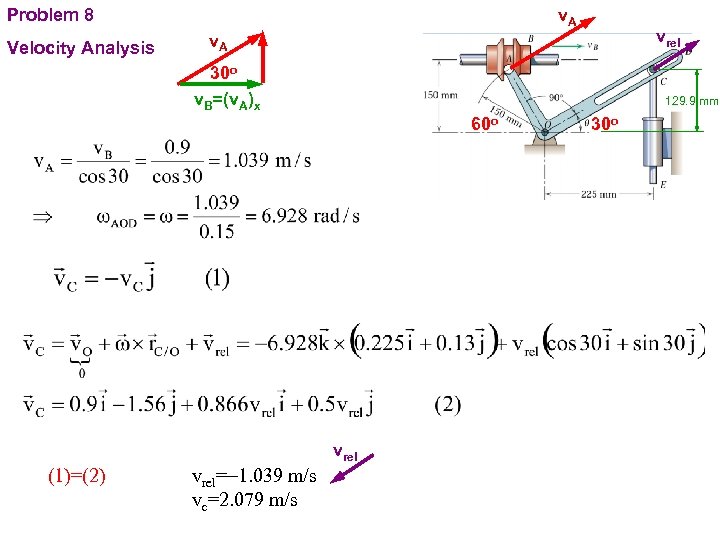
v. A Problem 8 Velocity Analysis vrel v. A 30 o v. B=(v. A)x 129. 9 mm 60 o vrel (1)=(2) vrel=-1. 039 m/s vc=2. 079 m/s 30 o

Acceleration Analysis a. A 30 (a. A)n o VB=constant So a. A must be vertical. (a. A)t vrel a. A 60 o 30 o 129. 9 mm
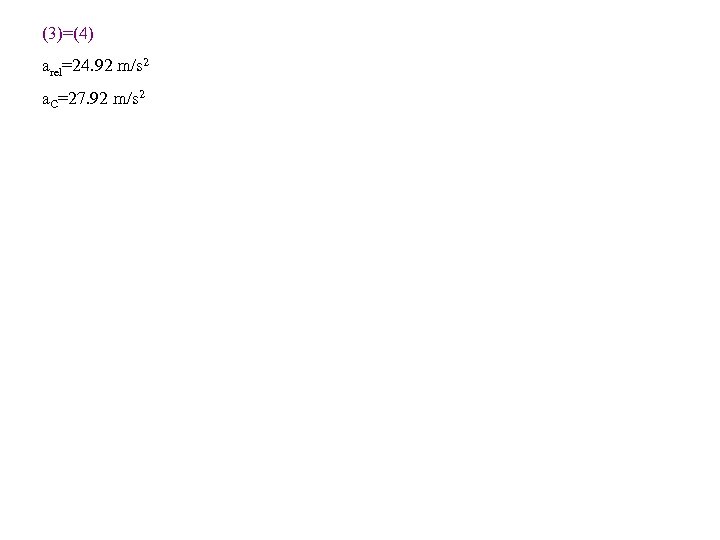
(3)=(4) arel=24. 92 m/s 2 a. C=27. 92 m/s 2
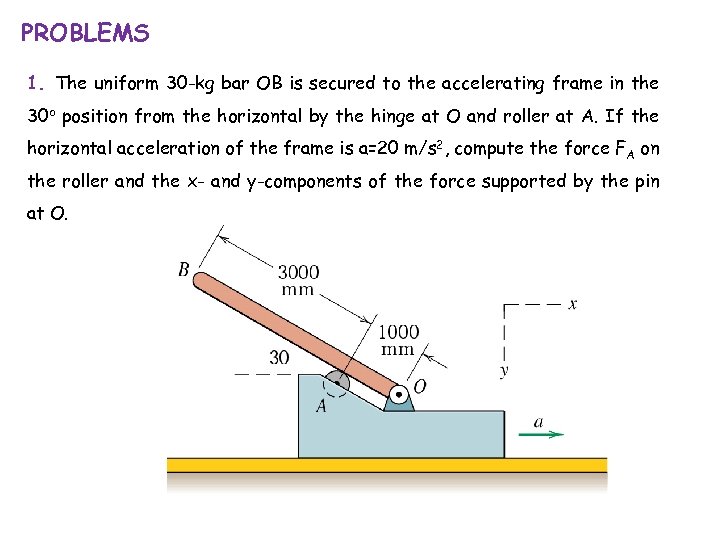
PROBLEMS 1. The uniform 30 -kg bar OB is secured to the accelerating frame in the 30 o position from the horizontal by the hinge at O and roller at A. If the horizontal acceleration of the frame is a=20 m/s 2, compute the force FA on the roller and the x- and y-components of the force supported by the pin at O.
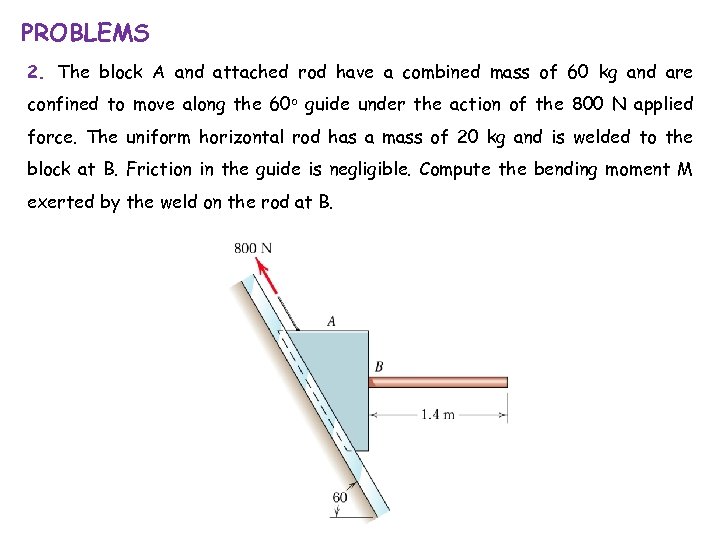
PROBLEMS 2. The block A and attached rod have a combined mass of 60 kg and are confined to move along the 60 o guide under the action of the 800 N applied force. The uniform horizontal rod has a mass of 20 kg and is welded to the block at B. Friction in the guide is negligible. Compute the bending moment M exerted by the weld on the rod at B.
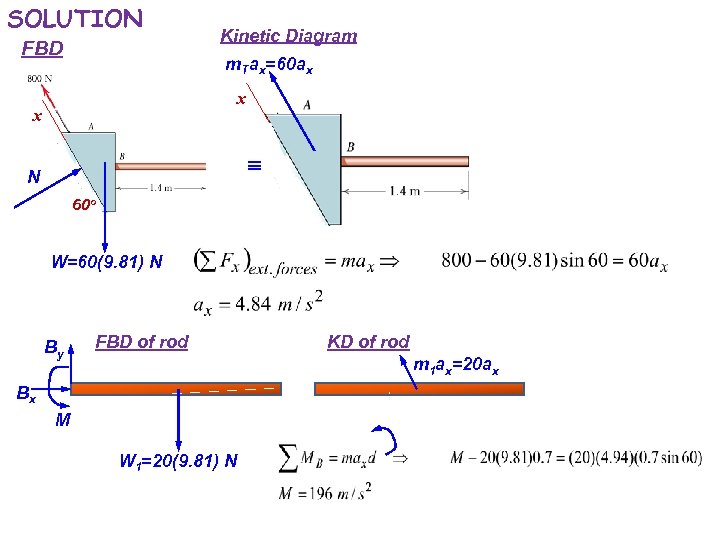
SOLUTION FBD Kinetic Diagram m. Tax=60 ax x x N 60 o W=60(9. 81) N By FBD of rod KD of rod m 1 ax=20 ax Bx M W 1=20(9. 81) N
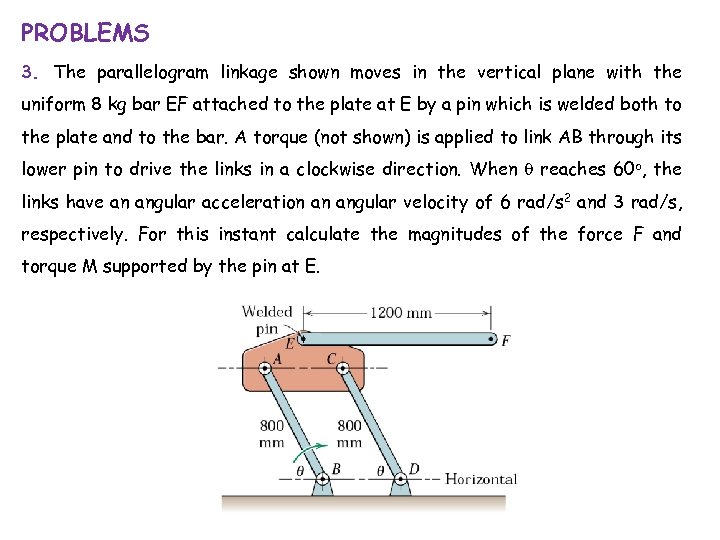
PROBLEMS 3. The parallelogram linkage shown moves in the vertical plane with the uniform 8 kg bar EF attached to the plate at E by a pin which is welded both to the plate and to the bar. A torque (not shown) is applied to link AB through its lower pin to drive the links in a clockwise direction. When q reaches 60 o, the links have an angular acceleration an angular velocity of 6 rad/s 2 and 3 rad/s, respectively. For this instant calculate the magnitudes of the force F and torque M supported by the pin at E.
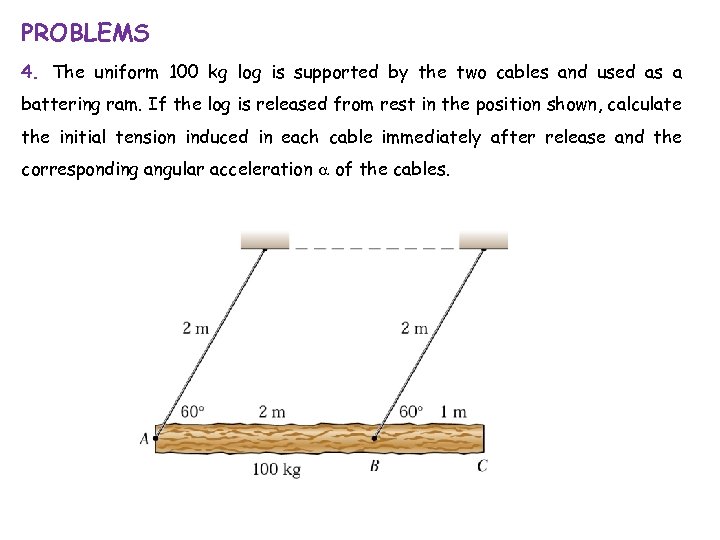
PROBLEMS 4. The uniform 100 kg log is supported by the two cables and used as a battering ram. If the log is released from rest in the position shown, calculate the initial tension induced in each cable immediately after release and the corresponding angular acceleration a of the cables.
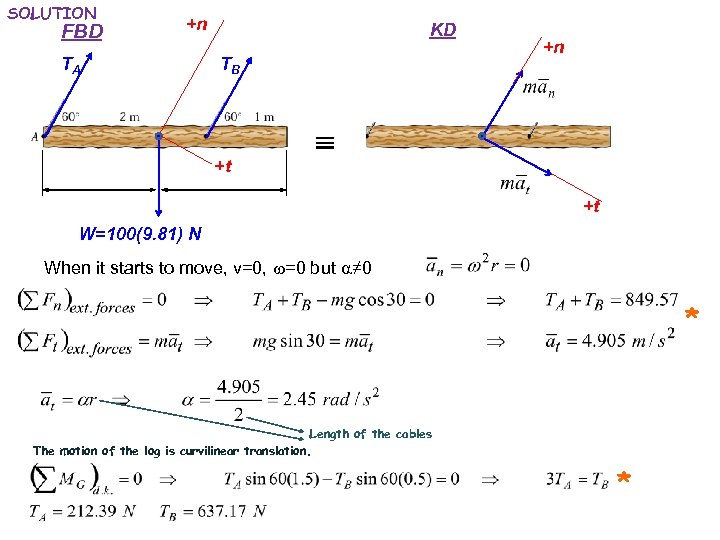
SOLUTION FBD +n TA KD TB +t +n +t W=100(9. 81) N When it starts to move, v=0, w=0 but a≠ 0 * Length of the cables The motion of the log is curvilinear translation. *
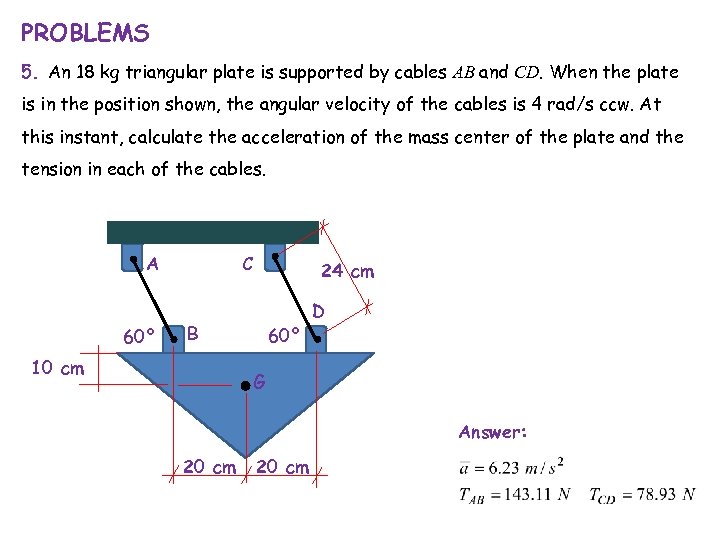
PROBLEMS 5. An 18 kg triangular plate is supported by cables AB and CD. When the plate is in the position shown, the angular velocity of the cables is 4 rad/s ccw. At this instant, calculate the acceleration of the mass center of the plate and the tension in each of the cables. C A 60° 24 cm B 10 cm 60° D G Answer: 20 cm
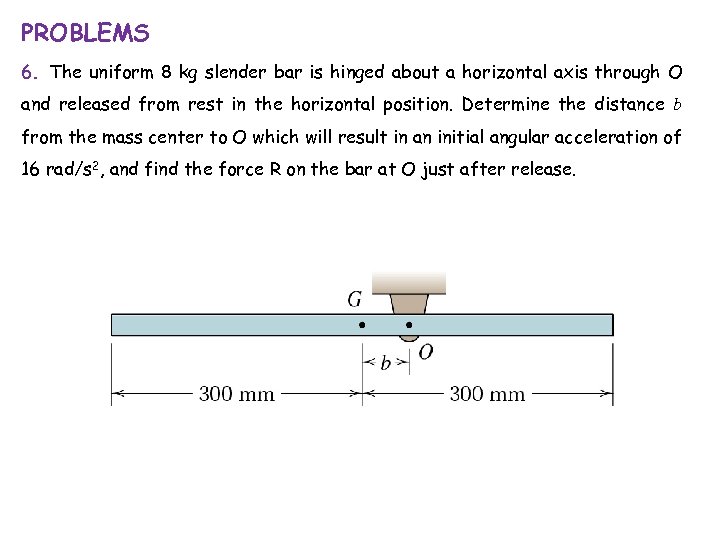
PROBLEMS 6. The uniform 8 kg slender bar is hinged about a horizontal axis through O and released from rest in the horizontal position. Determine the distance b from the mass center to O which will result in an initial angular acceleration of 16 rad/s 2, and find the force R on the bar at O just after release.
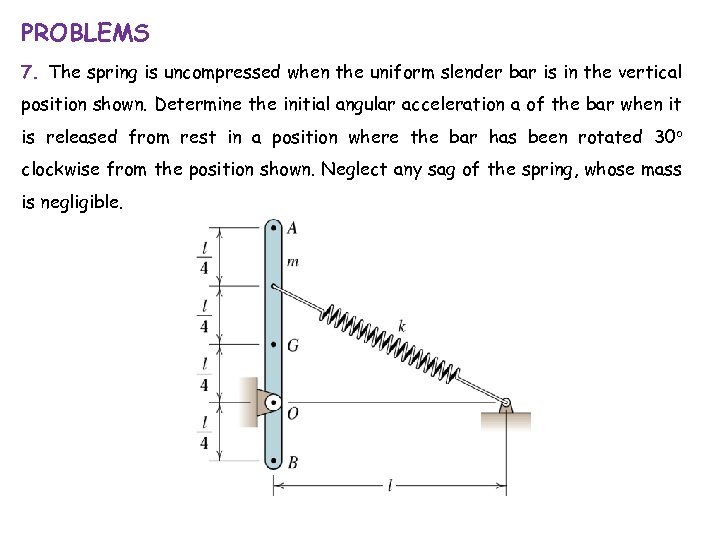
PROBLEMS 7. The spring is uncompressed when the uniform slender bar is in the vertical position shown. Determine the initial angular acceleration a of the bar when it is released from rest in a position where the bar has been rotated 30 o clockwise from the position shown. Neglect any sag of the spring, whose mass is negligible.

SOLUTION Unstrecthed length of the spring: When q=30 o , length of the spring: When q=30 o , spring force: (in compression) 30 o W +t Fspring . 60 o Ot +n O lspring G 60 o 30 o l On +t +n G
2599bbc0dfc09a449d27f27d6d3663da.ppt