Проблема оптимизации активных геофизических мониторинговых систем С Хайретдинов

Проблема оптимизации активных геофизических мониторинговых систем. С. Хайретдинов М. С. , Воскобойникова Г. М. ИВМи. МГ СО РАН 13 -ая Международная Азиатская школа-семинар, 18 -22 сентября 2017 г. Новосибирск

Аннотация. На сегодня вибросейсмический метод просвечивания Земли (ВПЗ) находит распространение в решении большого спектра геофизических задач, таких как мониторинг сейсмоопасных зон, сейсмическая томография, калибровка сейсмотрасс и сейсмостанций для повышения точности определения координат землетрясений и ядерных взрывов и ряд других. Решение таких задач - связано с большими энергетическими затратами, превосходящими 20 мвт-час. при просвечивании на расстояниях свыше 1000 км.

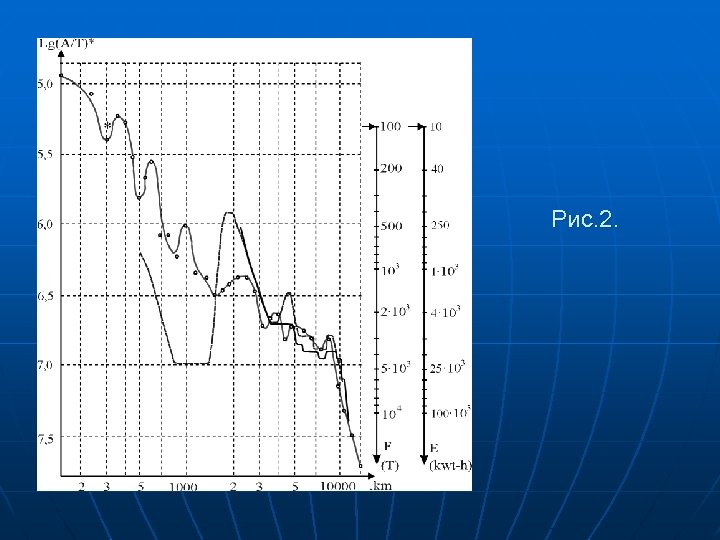
Рис. 2.

Минимизация энергетических затрат при заданном качестве функционирования системы ВПЗ постоянно является актуальной задачей. В предлагаемой работе анализируются пути решения поставленной задачи методами оптимизации структуры и параметров системы ВПЗ, изучения и учета особенностей процессов излучения и распространения сейсмических волновых полей

Постановка задачи. В обобщенном виде процесс вибрационного зондирования Земли может быть описан уравнением где - импульсная функция среды для координат излучателя и приемника ; - зондирующий сигнал, - шум в точке регистрации, - отклик среды в виде сейсмограммы в ответ на зондирование.

Качество измерения параметров сейсмограммы на фоне многократно превосходящих шумов может быть охарактеризовано отношением сигнал/шум в виде: Здесь в числителе энергия волн P, S в полосе частот зондирования соответственно, в знаменателе – энергия шума в той же полосе.

Параметр является в общем случае функционалом от ряда параметров системы ВПЗ: Здесь - энергии сейсмических волн P и S в точке излучения; - расстояние излучательприемник , -параметры зондирующего сигнала и шума, представленные в виде соответствующих корреляционных функций, - оператор обработки регистрируемых сигналов.

В математическом плане задача оптимизации формулируется как достижение некоторого *2 = мах( 2 ) при E = const, т. е. получение максимума помехоустойчивости системы ВПЗ при постоянстве энергии потребления вибратором Е.

Задача оптимизации n n Задача оптимизации рассматривается как задача исследования операций в интересах построения вибросейсмический системы в соответствии с заданными критериями. Под операцией подразумевается комплекс мероприятий, направленных на достижение поставленной цели. Отыскание наилучшего способа реализации операции связано с построением математической модели, выборе критерия эффективности, выборе стратегий- способов достижения цели. Рассмотрение их является целью настоящего доклада.

Приближенное уравнение критерия эффективности где - для продольных волн, - для поперечных волн, - плотность среды под вибратором, Т - время зондирования, n = -1 – для объемной волны, =2. 5 10 -4 f 0 км -1, VP, VS – скорости продольных и поперечных волн в среде под вибратором.

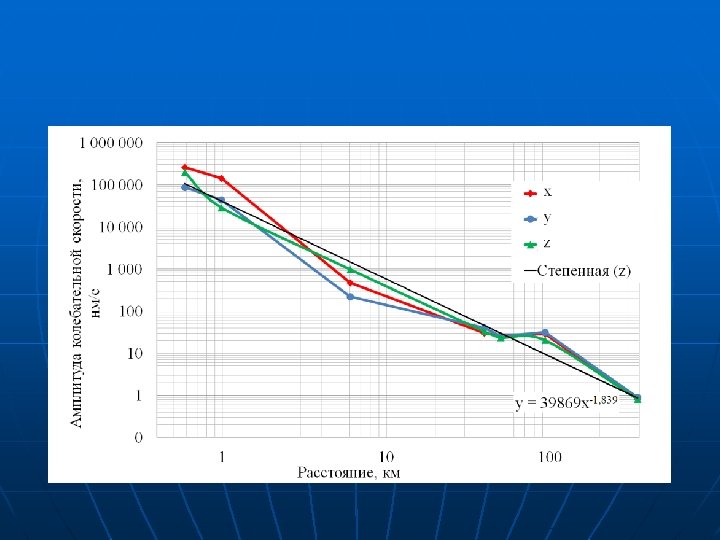
Стратегии достижения цели: • резонансноесогласование вибратора с грунтом, описываемого моделью многослойной среды. Это позволяет поднять на порядок и более эффективность преобразования энергии потребления в энергию сейсмических волн- доказано теоретически и экспериментально; • учет соотношения частотно-зависимых свойств среды распространения волн и спектров микросейсм; • оптимизация алгоритма обработки L[u(t)]; • оптимизации выбора типов зондирующих сигналов -1 (с линейной и фазовой модуляцией, монохроматических сигналов) • учет нелинейных эффектов распространения сейсмических волн.

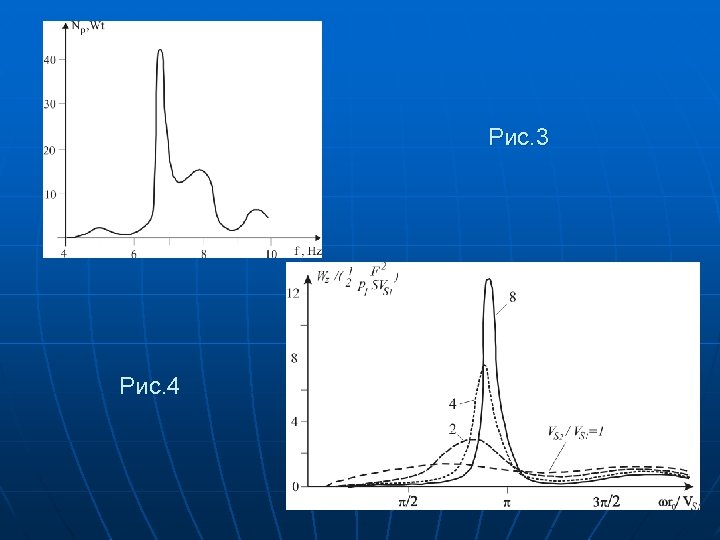
Рис. 3 Рис. 4

Учет частотно зависимых свойств среды распространения волн и характеристик микросейсм. Для модели квазиоднородного олупространства, достаточной для получения приближенных оценок уровней колебаний на больших расстояниях (до 1000 км), частотная характеристика среды описывается выражением G( )= A 0 /r exp (- r /2 ) Сейсмический шум при этом N( )=D exp ( - /2 ) /(1+ /2 ) Здесь D – дисперсия шума, - коэффициент, определяющий крутизну спада огибающей спектра шума в зависимости от частоты. В расчетах принималось экспериментально определенное значение =0. 025.

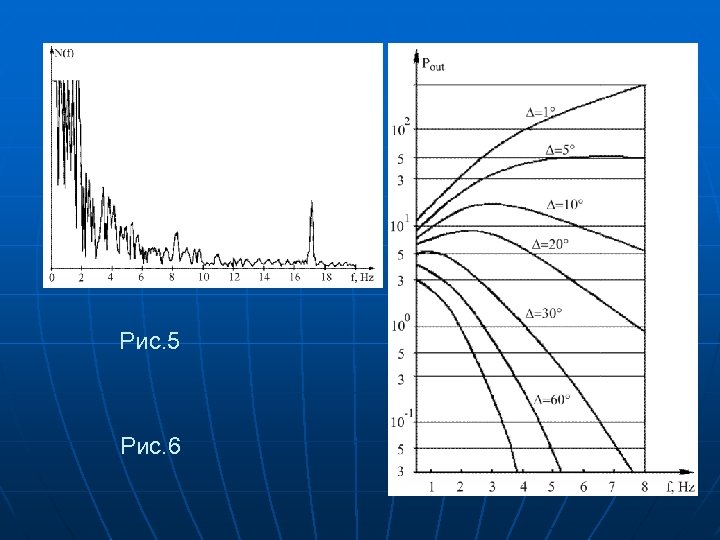
Рис. 5 Рис. 6

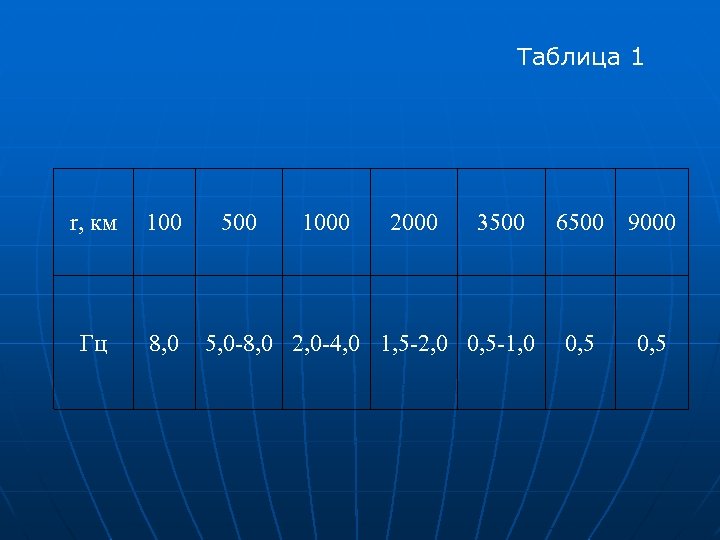
Таблица 1 r, км 100 Гц 8, 0 500 1000 2000 3500 5, 0 -8, 0 2, 0 -4, 0 1, 5 -2, 0 0, 5 -1, 0 6500 9000 0, 5

Оптимизация алгоритма обработки вибросейсмических сигналов( выбор оператора обработки L[u(t)] ). , где m=1, . . . , L. Здесь , где Gp, s ( fi ) –спектрограммы волн P и S ; Di – дисперсия шума на частоте fi ; L - число отсчетов вибрационной сейсмограммы; N - число отсчетов входного сигнала u(t).

Оптимизация выбора типов зондирующих сигналов. Для классов зондирующих сигналов S(t) с корреляционной функцией критерий эффективности : - нормированная корреляционная функция среды, - энергия зондирующего сигнала, - спектральная плотность помехи. Из (5) следует, что при фиксированной энергии наиболее высокой помехоустойчивостью (т. е. максимумом ) в отношении такой сложно построенной среды распространения волн как Земля обладают сигналы с протяженной функцией. Этому требованию отвечают узкополосные сигналы, в частности, монохроматические.

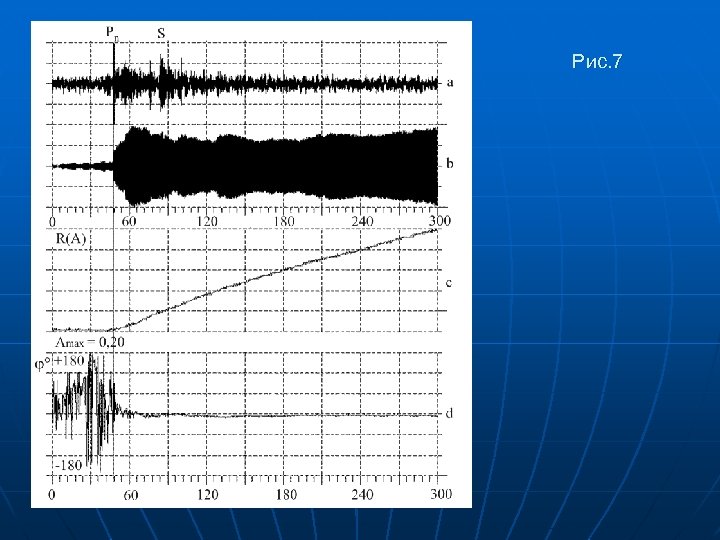
Рис. 7

Учет нелинейных эффектов распространения сейсмических волн Для случая распространения в моделируемой среде плоских монохроматических упругих волн вдоль оси ОХ при наличии только продольных движений в среде ( ) уравнение распространения имеет вид: (10)

При граничном условии решение уравнения во втором приближении примет вид: (11) где , ,

Из выражения (11) следует, что в трещиноватой среде появляются гармоники удвоенной частоты, уровень которых определяется коэффициентом B, зависящим от характера трещиноватости среды, числом Маха и длиной пути пробега волны x. В последнем случае уровень второй гармоники растет пропорционально x. Это явление было отмечено еще ранее как накапливающаяся нелинейность в нелинейноупругой среде. С учетом (11) коэффициент нелинейности формы монохроматической волны, определяемой отношением амплитуды первой гармоники ко второй, составит (12)

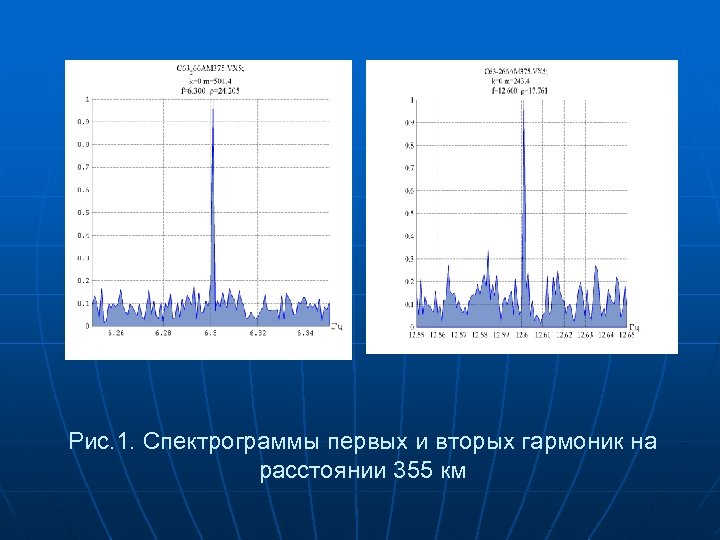
Рис. 1. Спектрограммы первых и вторых гармоник на расстоянии 355 км

Заключение 1. Проанализированы возможные пути и разработаны рекомендации по оптимизации системы глубинного вибрационного зондирования Земли. Наиболее эффективные из них связаны с резонансным согласованием вибратора с подстилающей средой и выбором монохроматических зондирующих сигналов и учетом нелинейных эффектов излучения и распространения сейсмических волн. При этом возможно увеличение эффективности вибрационного зондирования до двух порядков. при неизменной энергии потребления вибратором. Это обстоятельство особенно важно, когда зондирование осуществляется на расстояниях, близких к телесейсмическим. 2. При монохроматическом методе зондирования возможно достижение повышенной точности измерения динамических характеристик волновых полей, прежде всего параметров амплитуд и фаз колебаний во множестве точек пространства, где располагаются элементы площадной приемной антенны. Это позволяет проводить исследования по решению задач сейсмической томографии , изучению геодинамических процессов в коре и верхней мантии и др.

Спасибо за внимание!