Проблема индукции универсальность нейронных сетей базис

Проблема индукции + универсальность нейронных сетей + базис нелинейной динамики А. С. Потапов, М. В. Петерсон, А. И. Свитенков

Проблема индукции Простейшая постановка • Построение модели для предсказания численной последовательности • Пространство моделей? • Критерий выбора? 2

Пример: полиномиальная аппроксимация • Любая гладкая функция на некотором промежутке может быть сколь угодно точно приближена полиномами => Минимизация ошибки • Линейным МНК 3

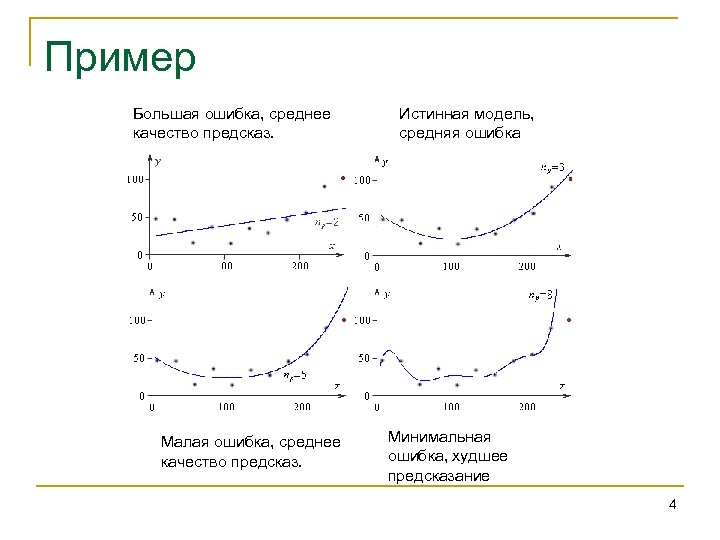
Пример Большая ошибка, среднее качество предсказ. Малая ошибка, среднее качество предсказ. Истинная модель, средняя ошибка Минимальная ошибка, худшее предсказание 4

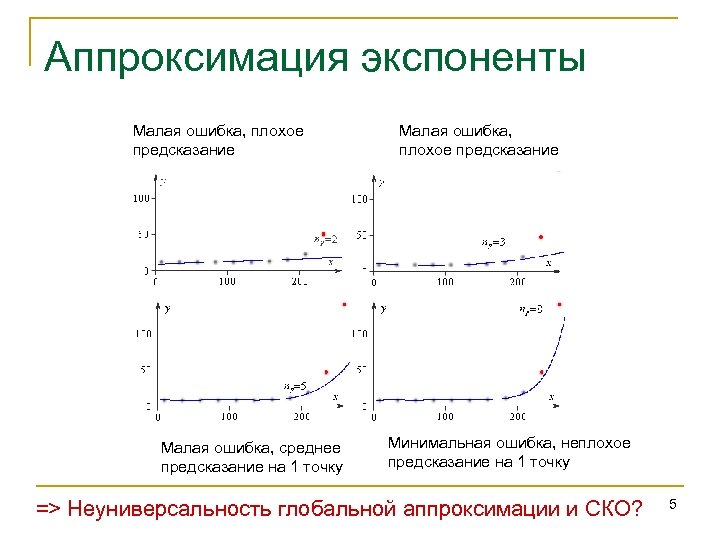
Аппроксимация экспоненты Малая ошибка, плохое предсказание Малая ошибка, среднее предсказание на 1 точку Малая ошибка, плохое предсказание Минимальная ошибка, неплохое предсказание на 1 точку => Неуниверсальность глобальной аппроксимации и СКО? 5

Байесовский подход • Критерий в форме апостериорной вероятности D – данные; H – модель (описание) • Представление данных – в форме плотности P(D|H) и априорного распределения P(H) • Например где f – полином с параметрами w - нормальное распределение ошибок аппрокс. - априорная вероятность появления полинома 6

Проблемы байесовского подхода • Максимизация P(D|H) соответствует минимизации невязок (при нормальном распределении) – метод максимального правдоподобия близок к МНК • Возможность выбрать «неоптимальную» по СКО модель имеется только за счет априорных вероятностей P(H), которые неизвестно, как задавать • Остаются проблемы с аппроксимацией непредусмотренных зависимостей 7

Алгоритмически полное пространство – универсальное пространство моделей • Программа печатает знаки числа е, оперируя целыми числами main(){int N=9009, n=N, a[9009], x; while(--n)a[n]=1+1/n; for(; N>9; printf("%d", x)) for(n=N--; --n; a[n]=x%n, x=10*a[n-1]+x/n); } • Любые мыслимые функции (и закономерности) представляются (сравнительно компактными) алгоритмами • Аппроксимация фиксированной системой функций – работа в неалгоритмически полном пространстве моделей 8

Универсальный критерий • Длина алгоритма, порождающего данные, - критерий его качества как модели этих данных • Теоретическое рассмотрение U – универсальная машина Тьюринга; K – алгоритмическая сложность l – длина строки H 0 – лучшее описание данных; Лучшее неточное описание: => УМТ задает универсальное априорное распределение и пространство моделей 9

«Универсальные» проблемы • Крайне затруднителен поиск в алгоритмически полном пространстве • Выбор универсальной машины произволен • Невозможно задать априорную информацию (индукция осуществляется по всем имеющимся данным) • Практическое использование Длины описаний вычисляются в рамках эвристически заданных схем кодирования данных Принцип минимальной длины описания (МДО) используется как рекомендация к выводу частных критериев Нет формального определения понятия представления и критериев его оптимизации 10

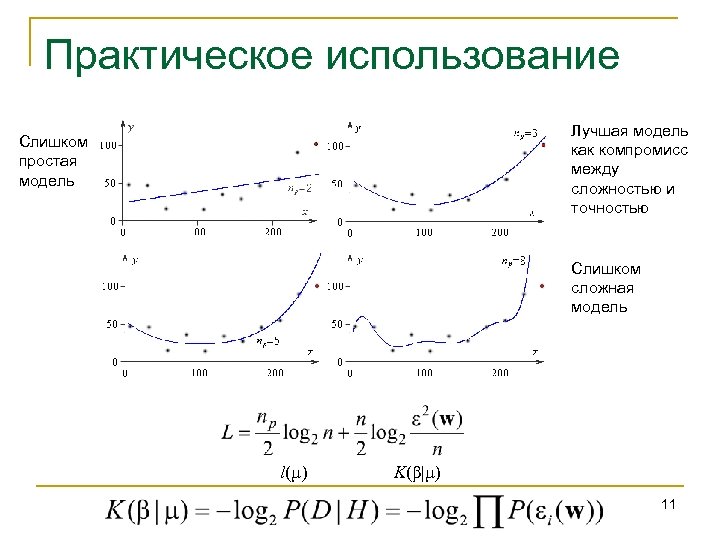
Практическое использование Лучшая модель как компромисс между сложностью и точностью Слишком простая модель Слишком сложная модель l(µ) K(β|µ) 11

Принцип репрезентационной МДО Задачи индукции обычно ставятся как массовые проблемы: один и тот же алгоритм независимо применяется к разных наборам данных • Определение Однако: Представлением для множества наборов данных D назовем такую программу S для УМТ U, что для любого набора данных d существует его описание h Можно показать, что • Принцип репрезентационной МДО • Лучшее описание данных имеет минимальную длину в рамках заданного представления • Лучшее представление данных минимизирует суммарную длину описания наборов данных обучающей выборки Преимущество: применимость к любому типу представлений 12

Основные проблемы • Нет универсальных практически приемлемых методов поиска, в частности: • В рамках задачи экстраполяции каждый тип функций приходится задавать по отдельности • Какие альтернативные универсальные аппроксиматоры имеются? 13

Свойства? ИНС • Обработка образной, а не символьной информации • Неалгоритмичность • Самообучаемость, самоорганизация • Воспроизведение свойств биологических нейронов 14

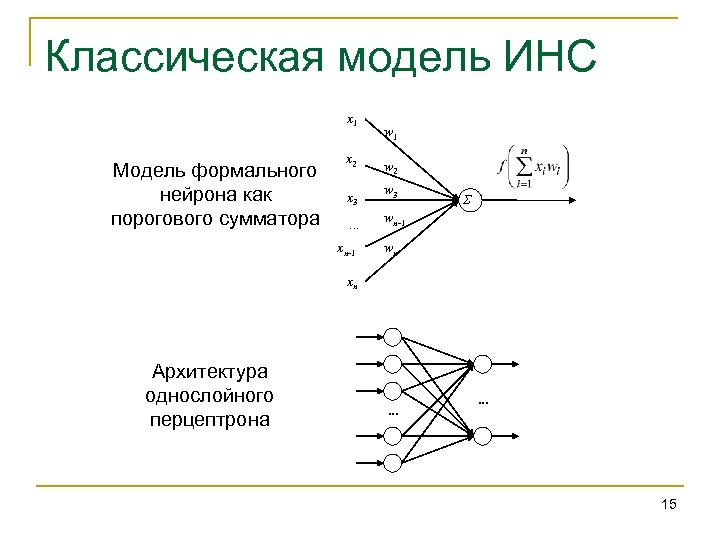
Классическая модель ИНС x 1 Модель формального нейрона как порогового сумматора x 2 x 3. . . xn-1 w 2 w 3 Σ wn-1 wn xn Архитектура однослойного перцептрона . . . 15

ИНС – универсальные аппроксиматоры? • Представление функций многих переменных композицией функций одной переменной (1957) • «Строгие результаты основаны на (а) теореме Колмогорова об аппроксимации функций сигмоидами, (б) ряде теорем, показывающих, что многослойные перцептроны являются универсальными аппроксиматорами…» * • Однако универсальность означает алгоритмическую полноту; перцептроны же задают ограниченный функциональный базис * А. Б. Потапов, М. К. Али «Нелинейная динамика обработки информации в нейронных сетях» 16

ИНС неалгоритмичны? • Эквивалентность ИНС Мак. Каллока-Питтса: • логике высказываний (1943) • конечным автоматам (1956) • Эквивалентность ИНС и УМТ (1990 -е)? • Превосходство ИНС над УМТ (1990 -2000 -е)? • Однако последние доказательства базируются на бесконечности количестве знаков у рациональных и вещественных чисел 17

ИНС неалгоритмичны? • Эквивалентность ИНС Мак. Каллока-Питтса: • логике высказываний (1943) • конечным автоматам (1956) • Эквивалентность ИНС и УМТ (1990 -е)? • Превосходство ИНС над УМТ (1990 -2000 -е)? • Однако последние доказательства базируются на бесконечности количестве знаков у рациональных и вещественных чисел ИНС – частный способ представления алгоритмов 18

Самообучаемость ИНС? • Общие правила обучения • правило Хебба • Специфичные алгоритмы обучения • Априорный выбор архитектуры ИНС èобучение ИНС – это поиск в пространстве алгоритмов, осуществляемый другим алгоритмом è Преимущество ИНС – «тотально параметризованное» представление алгоритмов с «гладкой метрикой» 19

Расширения ИНС • … • Спайковые сети • Адресация нейронов по идентификаторам • Нелинейные по входу сети • Сети с модулирующими нейронами • Нейроглиальные сети 20

Анализ нейросетевых представлений • Представимость любых алгоритмов с помощью ИНС • Универсальное обучение как поиск в алгоритмически полном пространстве • Сохранение «гладкости метрики» • Критерий эффективности нейросетевых представлений – принцип репрезентационной минимальной длины описания • Соответствие свойствам биологических нейронов?

Динамические типы ИНС* • Сети-функции • Динамические сети типа 1: X=начальные данные – Y=конечное состояние (аттрактор); • Динамические сети типа 2: X=параметры дин. сис. – Y=конечное состояние (аттрактор); • Гамильтоновы нейронные сети Можно добавить: Y=динамических выход, хотя «Как правило, существование функции Ляпунова для уравнений динамики сети и отсутствие сложной временной динамики считается большим достоинством» * * А. Б. Потапов, М. К. Али «Нелинейная динамика обработки информации в нейронных сетях»

Динамические ИНС как генеративные модели • Колмогоровская сложность: • Пусть H – нейронная сеть; U(H) – результат исполнения сети Мнение: «Судя по всему, метафора, сравнивающая работу мозга с деятельностью машины Тьюринга, отходит в прошлое» * Однако динамические ИНС типа 1 в точности ложатся под базовое определение алгоритмической сложности; УМТ – нелинейная динамическая система *Г. Г. Малинецкий и др. Нелинейная динамика: подходы, результаты, надежды

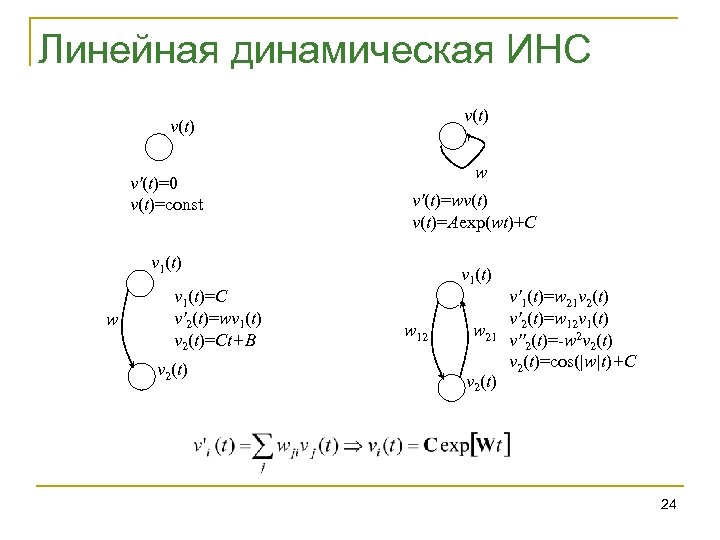
Линейная динамическая ИНС v(t) v'(t)=0 v(t)=const w v'(t)=wv(t)=Aexp(wt)+C v 1(t) w v 1(t)=C v'2(t)=wv 1(t) v 2(t)=Ct+B v 2(t) v 1(t) w 12 w 21 v 2(t) v'1(t)=w 21 v 2(t) v'2(t)=w 12 v 1(t) v''2(t)=-w 2 v 2(t)=cos(|w|t)+C 24

25

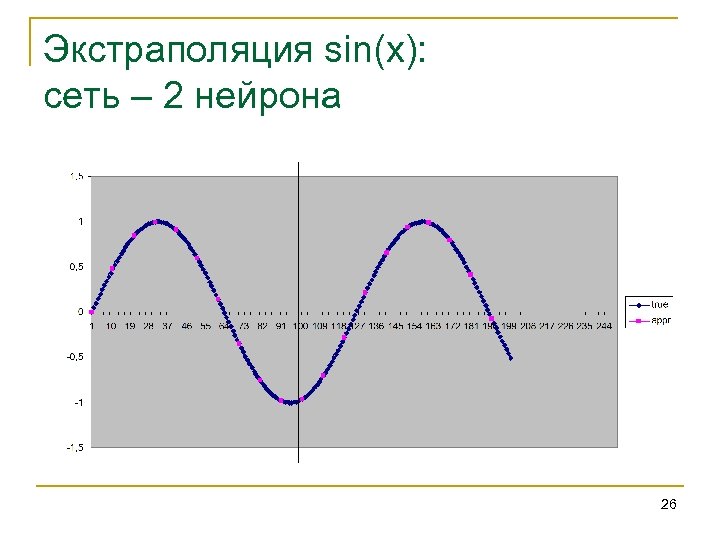
Экстраполяция sin(x): сеть – 2 нейрона 26

Альтернативное решение 27

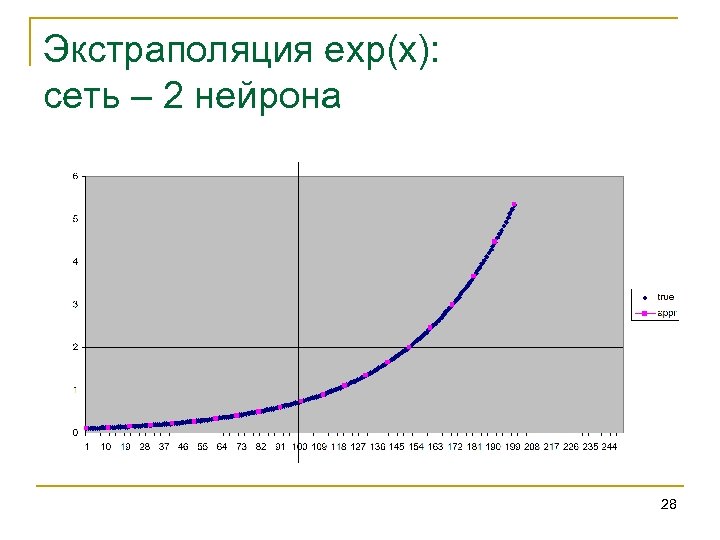
Экстраполяция exp(x): сеть – 2 нейрона 28

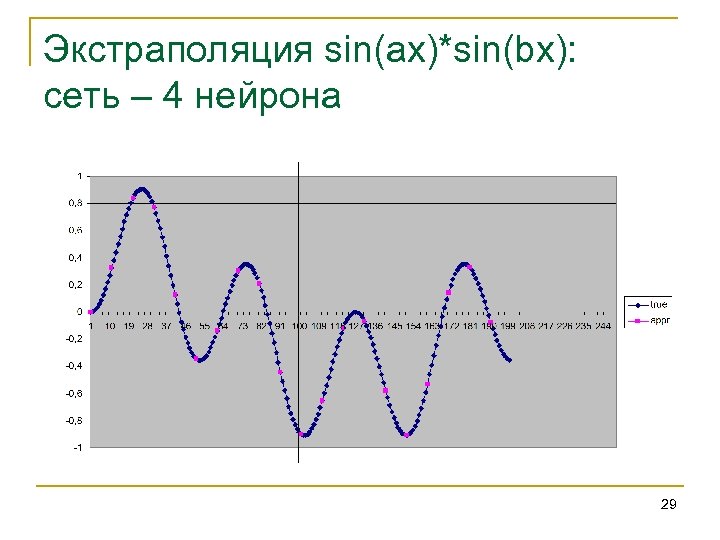
Экстраполяция sin(ax)*sin(bx): сеть – 4 нейрона 29

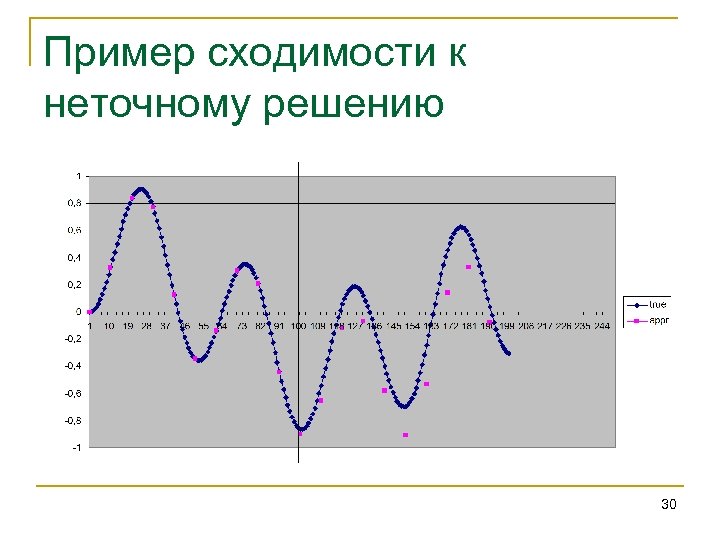
Пример сходимости к неточному решению 30

Обсуждение • В чем разница между системами дифференциальных уравнений и ИНС? • Как оптимально обучать (связи + начальная активность)? • Как выбирать архитектуру? 31

Проблемы выбора архитектуры • Выбор сложности • «…проблемы возникают при попытке аппроксимации слишком сложных функциональных зависимостей: чересчур простая сеть не способна дать правильную аппроксимацию, а очень уж сложная начинает усиливать шум (с этой проблемой в ее простейшем виде хорошо знаком каждый, кто сталкивался с задачей выбора степени полинома при полиномиальной аппроксимации одномерной зашумленной функции). Этот эффект был назван “overfitting”, и решение обычно ищется при помощи введения иерархических структур сети…» * • Выбор типа функции • Получить «чистые» полиномы в полносвязных сетях нереально… • Решается с помощью МДО * А. Б. Потапов, М. К. Али «Нелинейная динамика обработки информации в нейронных сетях» 32

Введение нелинейности как расширение представления • Способы • Нелинейная активационная функция • Внутренняя нелинейная динамика нейронов • Связи на связи • Требования • Нелинейность не должна «портить» представимость базовых функций • Семейство представимых функций должно максимально и единообразно расширяться Возможна явная оптимизация по РМДО 33

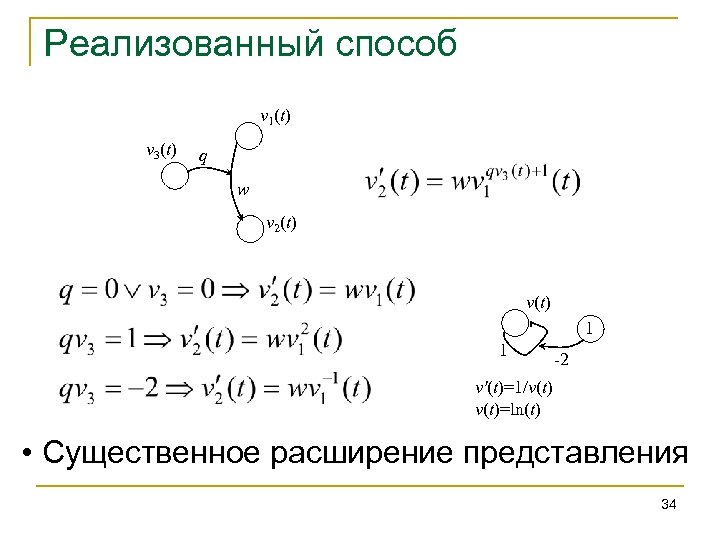
Реализованный способ v 1(t) v 3(t) q w v 2(t) v(t) 1 1 -2 v'(t)=1/v(t)=ln(t) • Существенное расширение представления 34

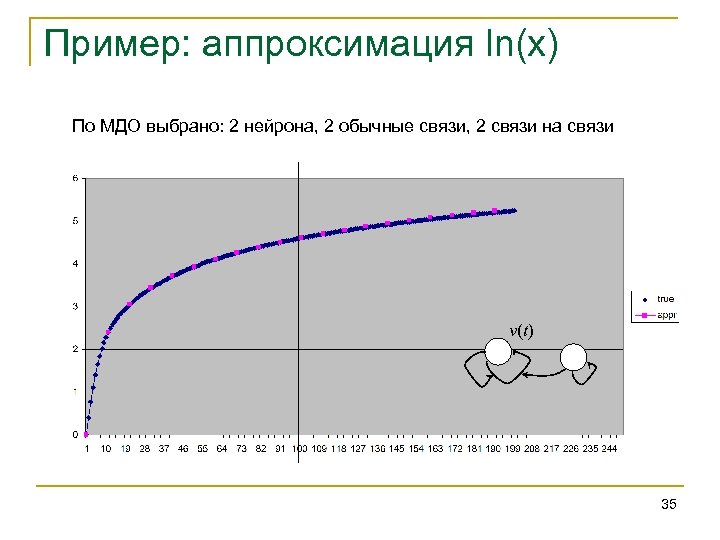
Пример: аппроксимация ln(x) По МДО выбрано: 2 нейрона, 2 обычные связи, 2 связи на связи v(t) 35

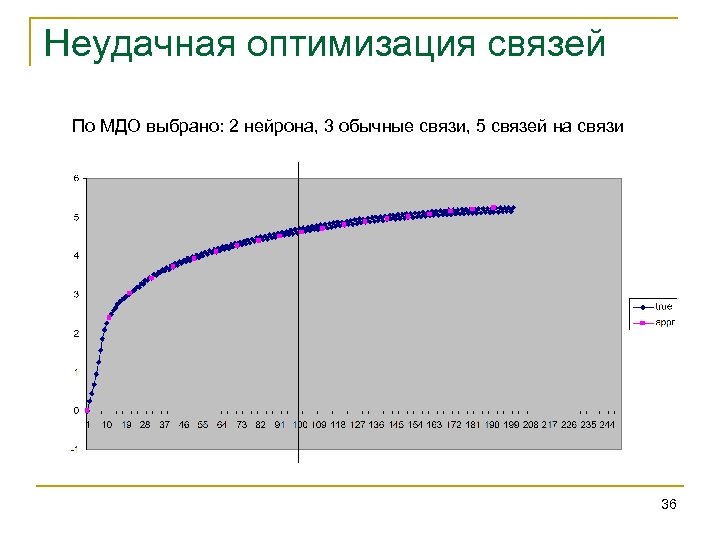
Неудачная оптимизация связей По МДО выбрано: 2 нейрона, 3 обычные связи, 5 связей на связи 36

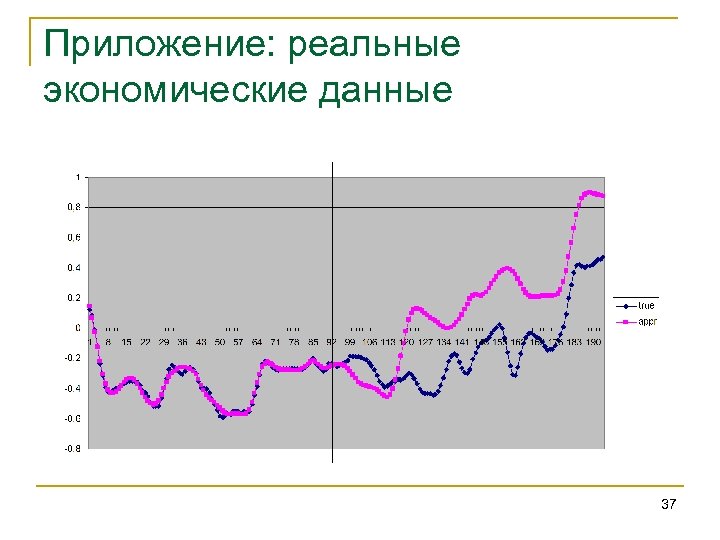
Приложение: реальные экономические данные 37

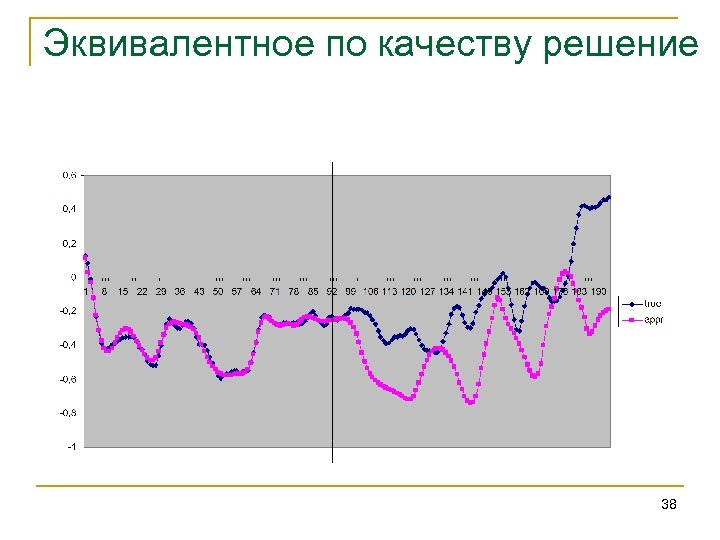
Эквивалентное по качеству решение 38

Добавление входного сигнала • Мнение: «Входной сигнал X можно подавать двумя основными способами: как начальные данные, либо как параметры динамической системы. Комбинирование этих путей, в принципе, возможно, но ни одна подобная сеть нам не известна» * • Однако в случае систем управления абсолютно естественно комбинировать эти способы * А. Б. Потапов, М. К. Али «Нелинейная динамика обработки информации в нейронных сетях» 39

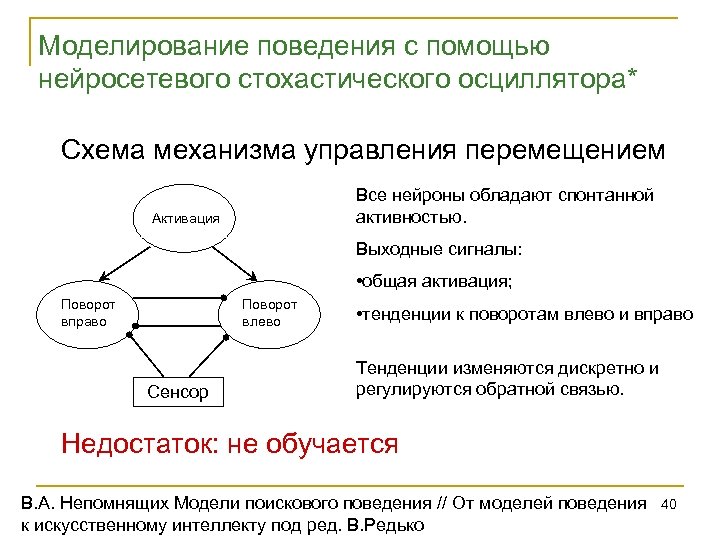
Моделирование поведения с помощью нейросетевого стохастического осциллятора* Схема механизма управления перемещением Все нейроны обладают спонтанной активностью. Активация Выходные сигналы: • общая активация; Поворот вправо Поворот влево Сенсор • тенденции к поворотам влево и вправо Тенденции изменяются дискретно и регулируются обратной связью. Недостаток: не обучается В. А. Непомнящих Модели поискового поведения // От моделей поведения к искусственному интеллекту под ред. В. Редько 40

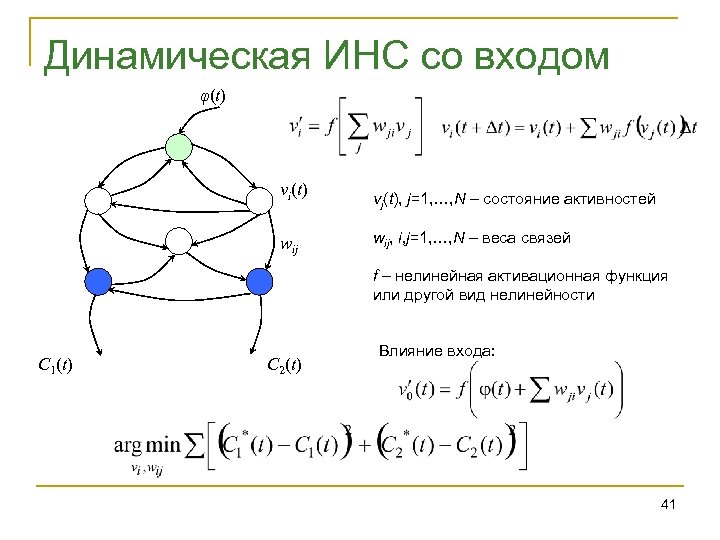
Динамическая ИНС со входом φ(t) vi(t) wij vj(t), j=1, …, N – состояние активностей wij, i, j=1, …, N – веса связей f – нелинейная активационная функция или другой вид нелинейности C 1(t) C 2(t) Влияние входа: 41

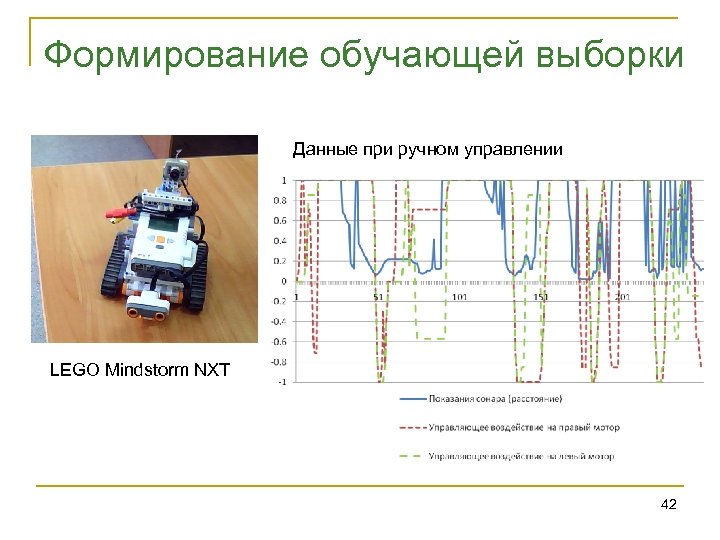
Формирование обучающей выборки Данные при ручном управлении LEGO Mindstorm NXT 42

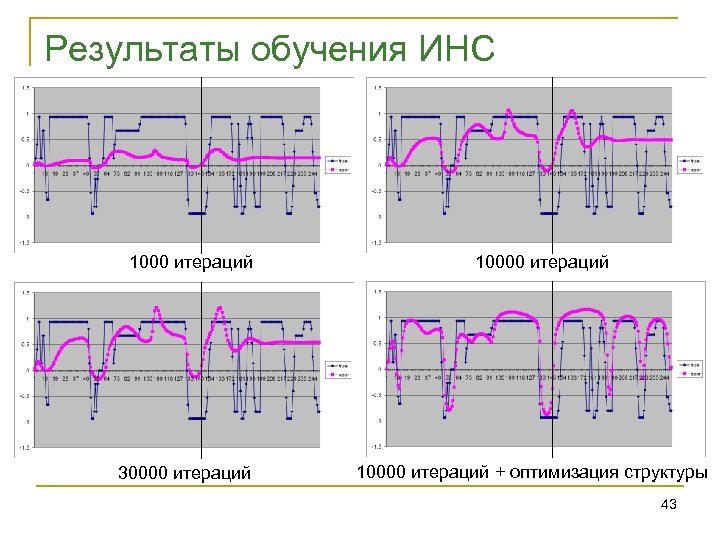
Результаты обучения ИНС 1000 итераций 30000 итераций 10000 итераций + оптимизация структуры 43

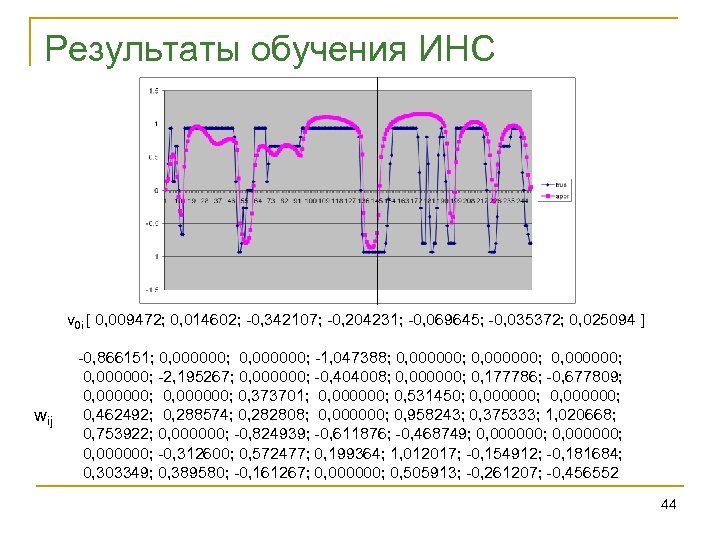
Результаты обучения ИНС v 0 i [ 0, 009472; 0, 014602; -0, 342107; -0, 204231; -0, 069645; -0, 035372; 0, 025094 ] wij -0, 866151; 0, 000000; -1, 047388; 0, 000000; -2, 195267; 0, 000000; -0, 404008; 0, 000000; 0, 177786; -0, 677809; 0, 000000; 0, 373701; 0, 000000; 0, 531450; 0, 000000; 0, 462492; 0, 288574; 0, 282808; 0, 000000; 0, 958243; 0, 375333; 1, 020668; 0, 753922; 0, 000000; -0, 824939; -0, 611876; -0, 468749; 0, 000000; -0, 312600; 0, 572477; 0, 199364; 1, 012017; -0, 154912; -0, 181684; 0, 303349; 0, 389580; -0, 161267; 0, 000000; 0, 505913; -0, 261207; -0, 456552 44

Работа ИНС при получении входа (t) 45

Общие проблемы • Трудная оптимизируемость (подгонка под данные) • Обучение часто сходится к сети с фазовым портретом, обладающим фокусом или предельным циклом (предсказание или поведение вырождается после переходного процесса) • Практическая невозможность аппроксимации динамического хаоса => Требуется не прямая аппроксимация данных, а восстановление фазового портрета 46

Обсуждение • Какие решения существуют? • ИНС как декларативное представление • На важность представлять свойства решений дифференциальных уравнений, не решая их, указывал Р. Фейман* • Восстановление фазового портрета • Противоречит ли аппроксимации? • И. Пригожин и И. Стенгерс полагают, что для хаотических систем траектория есть величина невоспроизводимая, а потому несущественная* • Противоречит ли МДО? • Доказана выделимость инвариантов по МДО, однако методы оптимизации не проработаны *Г. Г. Малинецкий, А. Б. Потапов. Современные проблемы нелинейной динамики 47