dd5c3b620fc5af0814333288cc82e8a0.ppt
- Количество слайдов: 25

Problem Solving – Six Steps 1. 2. 3. 4. Draw a sketch and label. List all numerical givens. Define what you Seek. Write an equation relating the variables. (formula) 5. Find a derivative. (Implicit and Chain Rules) 6. Evaluate and check unit labels. Classic Related Rates 1

Total area increases as the outer radius increases. A pebble is dropped into a calm pond, causing ripples in the form of concentric circles. The radius r of the outer ripple is increasing at a constant rate of 1 foot per second. When the radius is 4 feet, at what rate is the total area A of the disturbed water changing? Classic Related Rates 2
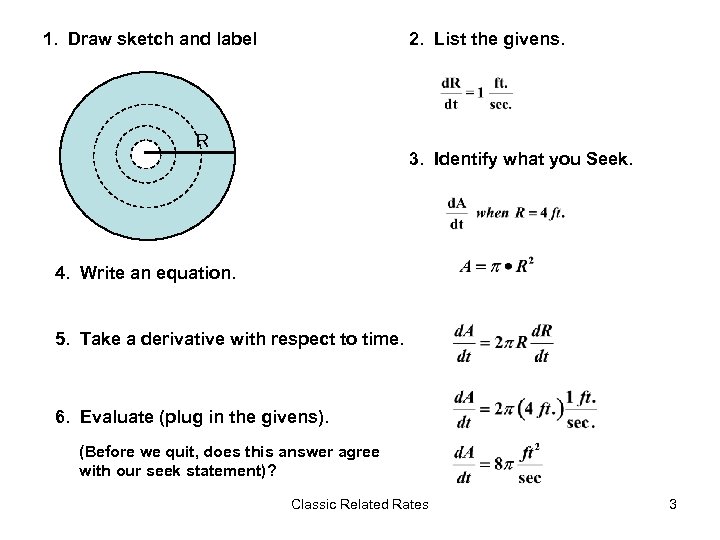
1. Draw sketch and label 2. List the givens. R 3. Identify what you Seek. 4. Write an equation. 5. Take a derivative with respect to time. 6. Evaluate (plug in the givens). (Before we quit, does this answer agree with our seek statement)? Classic Related Rates 3

Part #1: Air is being pumped into a spherical balloon at a rate of 5000 cc’s / min. How fast is the radius of the balloon changing at the instant the radius is: (a) 30 centimeters? Classic Related Rates 4

1. Draw sketch and label 2. List the givens. R 3. Identify what you Seek. 4. Write an equation. 5. Take a derivative with respect to time. 6. Evaluate (plug in the givens). (Before we quit, does this answer agree with our seek statement)? Classic Related Rates 5

Part #2 At the time when the volume and the radius of the sphere are increasing at the same numerical rate, what is the radius? Classic Related Rates 6

1. Draw sketch and label 2. List the givens. R 3. Identify what you Seek. 4. Write an equation. 5. Take a derivative with respect to time. 6. Evaluate (plug in the givens). (Before we quit, does this answer agree with our seek statement)? Classic Related Rates 7

A ladder 25 feet long is leaning against the wall of a house. The base of the ladder is pulled away from the wall at a rate of 14 feet per second. Classic Related Rates 8
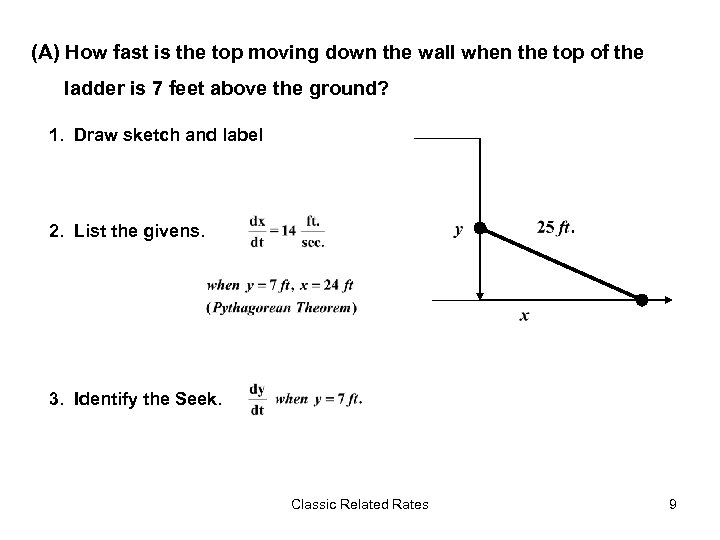
(A) How fast is the top moving down the wall when the top of the ladder is 7 feet above the ground? 1. Draw sketch and label 2. List the givens. 3. Identify the Seek. Classic Related Rates 9

(Part A continued) 4. Write an equation. 5. Differentiate implicitly. 6. Evaluate (plug in the givens). (Before we quit, does this answer agree with our seek statement)? Classic Related Rates 10

(B) Consider the triangle formed by the side of the house, the ladder, and the ground. Find the rate at which the area of the triangle is changing when the top of the ladder is 7 feet above the ground. 1. Draw sketch and label 2. List the givens. 3. Identify the find. Classic Related Rates 11

(Part B continued) 4. Write an equation. (area of a triangle) 5. Differentiate implicitly. 6. Evaluate (plug in the givens). (Before we quit, does this answer agree with our seek statement)? Classic Related Rates 12
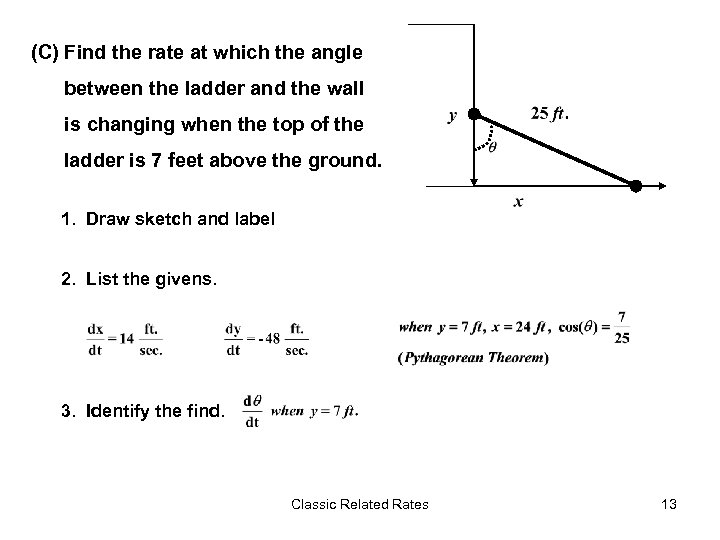
(C) Find the rate at which the angle between the ladder and the wall is changing when the top of the ladder is 7 feet above the ground. 1. Draw sketch and label 2. List the givens. 3. Identify the find. Classic Related Rates 13

(Part C continued) 4. Write an equation. 5. Differentiate implicitly. 6. Evaluate (plug in the givens). (Before we quit, does this answer agree with our seek statement)? Classic Related Rates 14

At a given moment a car is 30 miles north of an intersection, traveling toward the intersection at 45 mph. At the same time a truck is 40 miles east of the intersection, traveling away from the intersection at 35 mph. Is the distance between the vehicles increasing or decreasing at that moment? At what rate? Classic Related Rates 15
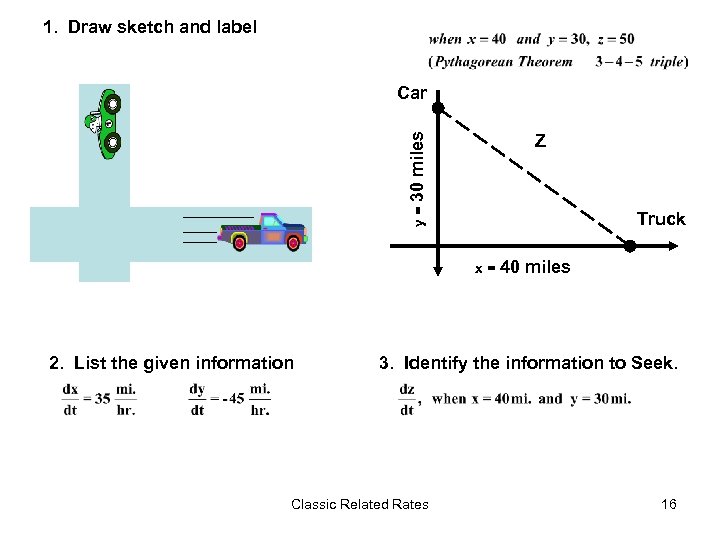
1. Draw sketch and label Car y= 30 miles Z Truck x= 2. List the given information 40 miles 3. Identify the information to Seek. Classic Related Rates 16

4. Write an equation. 5. Differentiate implicitly. 6. Evaluate (plug in the givens). Classic Related Rates 17

Water is flowing into a cone-shaped tank at the rate of 5 cubic inches per second. If the cone has an altitude of 4 inches and a base radius of 3 inches, how fast is the water level rising when the water is 2 inches deep? Classic Related Rates 18
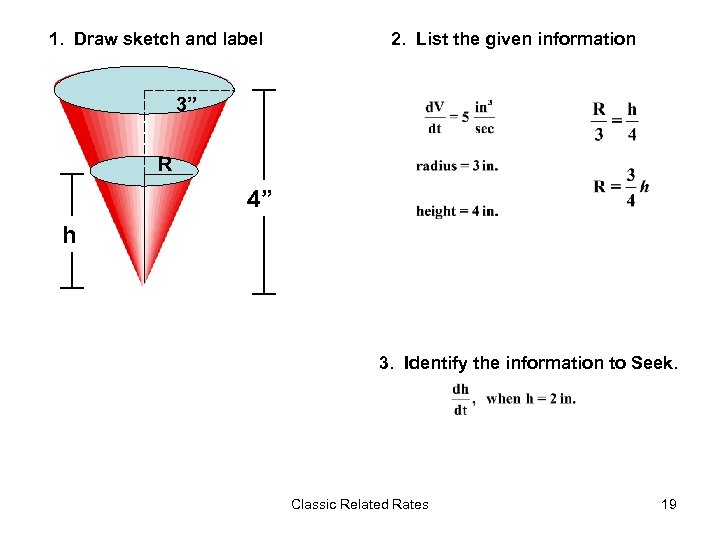
1. Draw sketch and label 2. List the given information 3” R 4” h 3. Identify the information to Seek. Classic Related Rates 19

4. Write an equation. Equation in 3 variables Equation in 2 variables 5. Differentiate implicitly. 6. Evaluate (plug in the givens). Classic Related Rates 20

Classic Related Rates 21
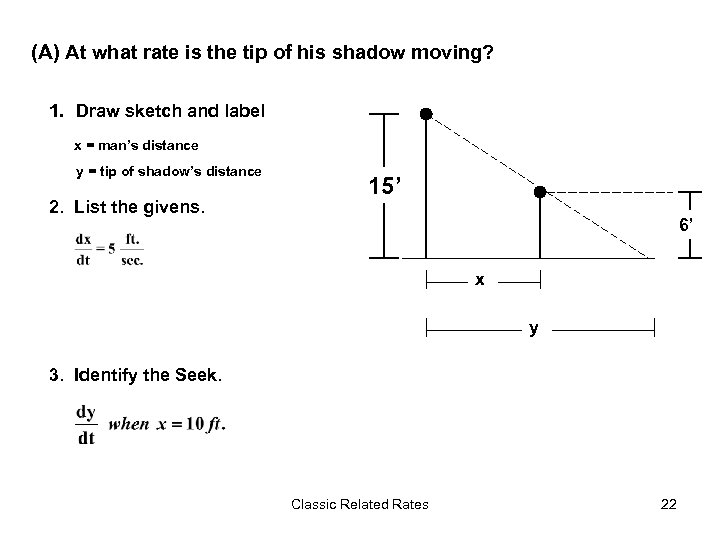
(A) At what rate is the tip of his shadow moving? 1. Draw sketch and label x = man’s distance y = tip of shadow’s distance 2. List the givens. 15’ 6’ x y 3. Identify the Seek. Classic Related Rates 22

(Part A continued) 4. Write an equation. Similar Triangles 5. Differentiate implicitly. 6. Evaluate (plug in the givens). Classic Related Rates 23
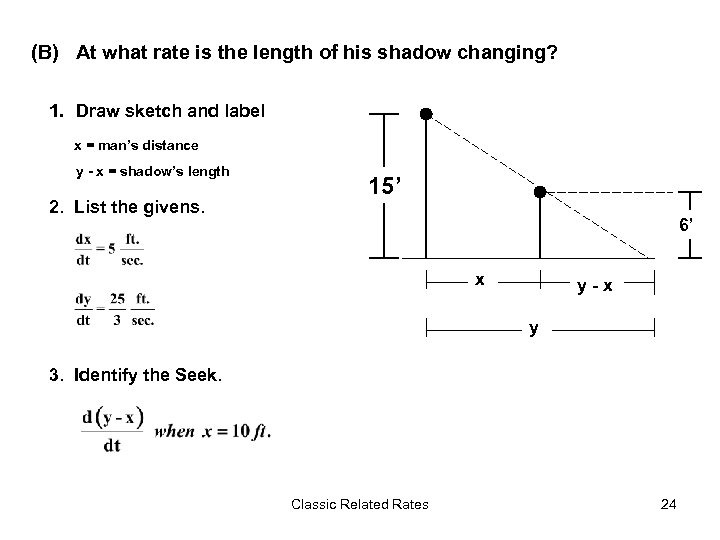
(B) At what rate is the length of his shadow changing? 1. Draw sketch and label x = man’s distance y - x = shadow’s length 2. List the givens. 15’ 6’ x y-x y 3. Identify the Seek. Classic Related Rates 24

(Part B continued) 4. Write an equation. Similar Triangles 5. Differentiate implicitly. 6. Evaluate (plug in the givens). Classic Related Rates 25
dd5c3b620fc5af0814333288cc82e8a0.ppt