Problem-Solving for Deaf Students Developing Skills in the

Problem-Solving for Deaf Students: Developing Skills in the Mathematics and Science Classroom Harry G. Lang Rachel C. Lewis National Technical Institute for the Deaf Rochester Institute of Technology

Objectives At the end of this lesson, teachers will be able to: • Explain the difference between true problem-solving and drill-andpractice exercises • Describe the five basic steps in the problem-solving process

Deaf Students & Problem-Solving • Previous research has identified some contributing factors to deaf students' difficulty in solving mathematics problems. Some of these factors include metacognitive skills, impulsivity, literacy and linguistic difficulty (Mousley & Kelly, 1998). Mousley, K. , & Kelly, R. (1998). Problem-solving strategies for teaching mathematics to deaf students. American Annals of the Deaf, 143, 325 -336.

Deaf Students & Problem-Solving For a detailed summary of research with deaf students in mathematics — especially problem-solving — see the “Best Practices in Mathematics Enhanced Literature Review” by Lang and Kelly at www. deafed. net

Deaf Students & Problem-Solving Survey of Problem-Solving Practices Grades 6 -12 (Kelly, Lang, Pagliaro 2003): • Teachers in center schools or selfcontained classes tend to perceive their students as having lower problemsolving ability as compared to integrated class teachers’ perspectives. This may be a function of student placement. • Teachers in integrated classes are less likely to view English ability as the primary barrier to problem-solving for their deaf students.

Deaf Students & Problem-Solving Survey of Problem-Solving Practices Grades 6 -12 (Kelly, Lang, Pagliaro 2003): • Teachers tend to focus on concrete visualizing strategies more than analytical strategies • Teachers tend to give students more practice with ‘practice problems’ rather than ‘true problems’. Kelly, R. , Lang, H. , & Pagliaro, C. (2003). Mathematics word problem solving for deaf students: A survey of practices in grades 6 -12. Journal of Deaf Sstudies and Deaf Education, 8, 104 -119.

Deaf Students & Problem-Solving • Teachers tend to give students more practice with ‘practice problems’ rather than ‘true problems’. • In this Power. Point lesson, we will focus on the difference between drill-andpractice exercises and “true problems, ” and we will provide some basic steps for solving true problems in mathematics and science.

What is mathematics? Cook (2001) identified 5 misconceptions regarding the teaching of mathematics: • mathematics is essentially computation • the important outcome in mathematics is the right answer • mathematics problems have only one right answer • there is only one right way to solve a problem • the teacher and the book should not be questioned Do you find yourself falling prey to any of these claims?

What is mathematics? The National Council of Teachers of Mathematics (NCTM) now stresses tasks that engage students in problem-solving and mathematical reasoning (Cook, 2001). Good problem-solving skills begin with good problems – problems which have no clear, pre-defined route to the solution. Presenting your students with such problems is a “best practice”. Cook, M. (2001). Mathematics: The thinking arena for problem-solving. In A. Costa (Ed. ), Developing Minds (3 rd ed. ). Alexandria, VA: Association for Supervision and Curriculum Development.

“True Problems” vs. “Drill” The difference can lie in both the problem itself and how the teacher presents it. If a teacher leads or hints too much, a good true problem can become a rote drill-and-practice problem. Working as an effective coach or guide is another “best practice”.

Teacher Questioning In clip PS 1, a teacher is discussing the difference between a foot and a square foot. She then asks formulas they’ve learned that involve square feet. Note that the teacher’s choice of questions forces students to dig a bit deeper than the less openended, “What units do we use to measure area? ” Film clip PS 1

“True Problems” vs. “Drill” Drill-and-Practice Example: Mary went to the store and spent $1. 55 for milk and $1. 70 for cookies. How much money did she spend? True Problem-Solving Example: Mary went to the store and spent $1. 55 for milk and $1. 70 for cookies. She handed the cashier $4. 00. How many coins could she receive if she received change in only nickels, dimes and quarters? Explain.

What is Problem-Solving? A drill-and-practice exercise does not require much thought. The operation is often very obvious. “True problem-solving” involves questions which seek an answer where neither the procedure nor the answer is obvious.

What is Problem-Solving? With true problem-solving… • There is more than one way to solve it. • There may be more than one answer. • There may be extraneous data, requiring students to identify the relevant data.

What is Problem-Solving? • In terms of challenging the student, true problems may sometimes not have sufficient data. Example: Soojin wants to buy three dolls that cost $6. 19 each, before sales tax is added. She has $20. Can she buy all three dolls? Explain. • In a problem such as this, you may either want students to recognize that there is not enough information (“We don’t know the sales tax rate”) or use the information they have to get a conditional answer (“If sales tax is 7. 7% or less, then she can buy all three”).

What is Problem-Solving? • True problems may lead the students to ask other questions. Example: What is the relationship between the circumference and the area of a circle? If the area of the circle increases, what will happen to the circumference? Explain your thinking. Inquisitive students may begin to look for patterns in the data.

Multiple Strategies (Flexibility) • Good problem-solvers do not rely on a single method, but are comfortable using a variety of strategies. They exhibit flexibility in their ability to choose the best approach for a given problem.

Possible Strategies • • • Guess-and-check Draw a picture Solve a simpler problem Make a table/graph Write an equation Act it out Look for a pattern Work backwards Conduct an experiment And others!

Characteristics of Good Problem-Solvers Good problem-solvers also have two other characteristics: a positive and determined attitude about problemsolving, and an awareness in the sense of understanding HOW they solved the problems (Lochhead & Zietsman, 2001). Lochhead, J. , & Zietsman, A. (2001). What is problem-solving? In A. Costa (Ed. ), Developing Minds (3 rd ed. ). Alexandria, VA: Association for Supervision and Curriculum Development.

Not Just Mathematics! • Problem-solving skills are necessary in a variety of areas. Strategies for improving such skills are especially applicable to science courses, such as biology, physics or chemistry.

‘True Problems’ in Science Biology Example: Kerstin has blue eyes. Her brother Mike has brown eyes. What can you conclude about their parents’ and grandparents’ eyes? This problem doesn’t have a single ‘right’ answer. All conclusions will be qualified, for example: • Both parents have at least one gene for blue eyes. • Only one parent might have blue eyes. • At least one out of each pair of grandparents has at least one gene for blue eyes.

‘True Problems’ in Science Physics Example: Victor hard-boiled a dozen eggs to make eggsalad for the picnic, but he’s forgotten which carton of eggs in the refrigerator holds the boiled eggs. Without breaking any eggshells, how can he figure out which carton of eggs to use? Explain your reasoning. This problem requires students to apply physical properties of matter without outlining which properties they should consider.

‘True Problems’ in Science Physics Example: Without breaking any eggshells, how can he figure out which carton of eggs to use? Explain your reasoning. Possible Answers: - Spin an egg from each carton on the table. The cooked egg will stop completely when lightly, quickly touched, because it’s solid and all stops together. - Shake an egg from each carton to settle the yolk in the raw egg. The raw egg can be balanced, with patience and a steady hand. (Relates to center of gravity. )

‘True Problems’ in Science Another Physics Example: How can you determine the height of a building using a barometer? This problem is more open-ended than it may appear. A college professor presented it to his deaf students and received the answers listed on the following slide. Would you accept any of the “alternative” answers?

‘True Problems’ in Science “Expected” Answer Measure the pressure at the top and bottom of the building and use the difference to calculate the height. Other “Correct” Answers - Drop the barometer off the top of the building, time how long it takes to hit the ground, and calculate the distance it traveled in that time. h= 1/2 gt 2

‘True Problems’ in Science “Expected” Answer Measure the pressure at the top and bottom of the building and use the difference to calculate the height. Other “Correct” Answers - Find the owner of the building and offer the barometer as a gift if you can see the blueprint of the building with the height given.

‘True Problems’ in Science “Expected” Answer Measure the pressure at the top and bottom of the building and use the difference to calculate the height. Other “Correct” Answers - Tie a string to the barometer and lower it until it reaches the ground. Then, measure the length of the string.

‘True Problems’ in Science “Expected” Answer Measure the pressure at the top and bottom of the building and use the difference to calculate the height. Other “Correct” Answers - Measure the barometer height (h), its shadow length (s) and the length of the building shadow (S). Then use proportions (similar triangles) to determine the building height (H) by H / S = h / s.

‘True Problems’ in Science Chemistry Example: The color of two different solutions appears to be identical. Think of a couple ways you could determine what the solutions are. Which method is best? Why? This problem is clearly open-ended. Students may think of many strategies — some outlandish — but will be asked to analyze their strategies in the end. Further restrictions can be added as you go, such as, “How could you safely determine which is which? ”

Best Practices In summary … • frequently assign TRUE problems that challenge thinking and help develop language skills • develop a positive attitude in your students about problem-solving

Beyond Problem Selection • Now that we have some ideas about the kinds of problems we can present to our students, we will look at a possible approach to solving those problems.

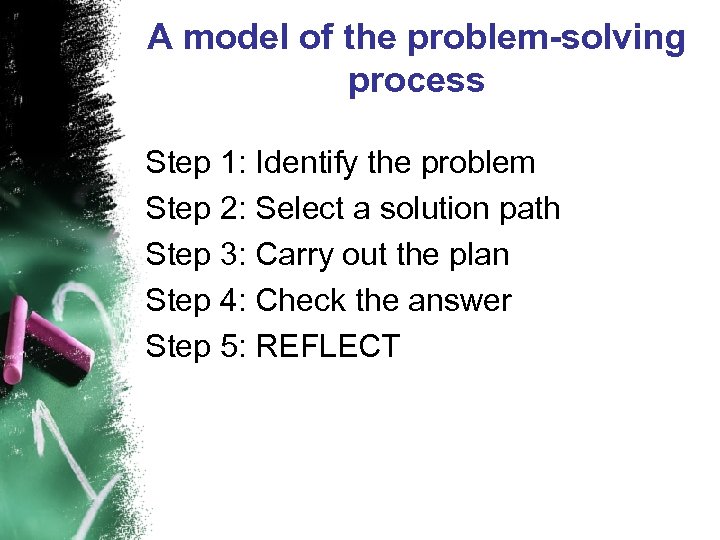
A model of the problem-solving process Step 1: Identify the problem Step 2: Select a solution path Step 3: Carry out the plan Step 4: Check the answer Step 5: REFLECT

Step 1: Problem Identification Stessi is trying to choose a pager company. Terrific Texting charges $12. 90 per month for their service and 5 cents per minute of use. Pretty-Good Pagers charges 15 cents per minute with no monthly fee. How can she decide which pager company will be less expensive? With a partner, come up with at least two explanations of what the real problem is. As a group, come to a consensus about the problem.

The Problem • It seems that which company Stessi chooses depends on how many minutes she expects to use the pager each month. • The real problem is to find the point where Pretty-Good Pagers becomes more expensive than Terrific Texting.

Step 2: Select a Solution Path Stessi is trying to choose a pager company. Terrific Texting charges $12. 90 per month for their service and 5 cents per minute of use. Pretty-Good Pagers charges 15 cents per minute with no monthly fee. How can she decide which pager company will be less expensive? As a group, brainstorm several ways one might go about solving this problem. Choose at least 3 solution paths to focus on.

Possible Strategies: • Make a table showing the cost of each company • Graph the cost of each company for x minutes of pager use • Write an equation for the cost of each company and solve symbolically • Others?

Step 3: Carry Out the Plan Stessi is trying to choose a pager company. Terrific Texting charges $12. 90 per month for their service and 5 cents per minute of use. Pretty-Good Pagers charges 15 cents per minute with no monthly fee. How can she decide which pager company will be less expensive? Divide into small teams, and each team should carry out one of the chosen solution paths. Be sure to record the processes used! You may want to designate one member of the group to serve as recorder.

PAUSE: Share Solutions Stessi is trying to choose a pager company. Terrific Texting charges $12. 90 per month for their service and 5 cents per minute of use. Pretty-Good Pagers charges 15 cents per minute with no monthly fee. How can she decide which pager company will be less expensive? One person from each group should share what they did, what worked and what didn’t, and the solution they reached. Comments from members of other groups should be shared and discussed.

Step 4: Check the Answer Stessi is trying to choose a pager company. Terrific Texting charges $12. 90 per month for their service and 5 cents per minute of use. Pretty-Good Pagers charges 15 cents per minute with no monthly fee. How can she decide which pager company will be less expensive? As a group, determine a process for checking the answer’s accuracy, listing the steps to be used.

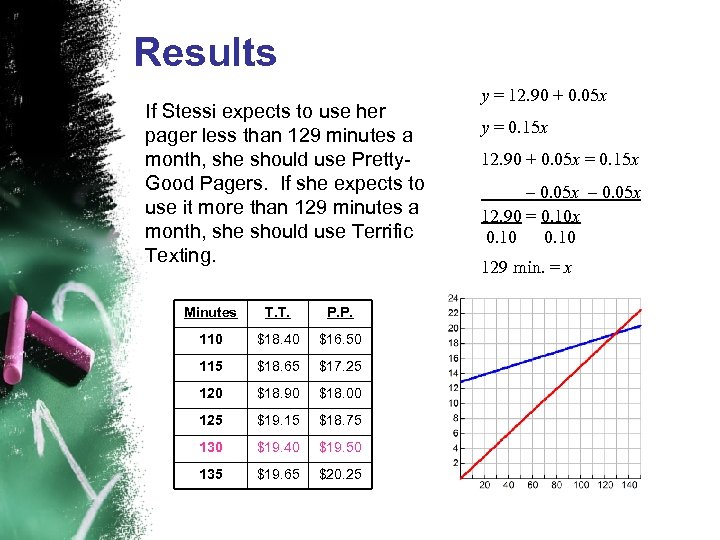
Results If Stessi expects to use her pager less than 129 minutes a month, she should use Pretty. Good Pagers. If she expects to use it more than 129 minutes a month, she should use Terrific Texting. Minutes T. T. P. P. 110 $18. 40 $16. 50 115 $18. 65 $17. 25 120 $18. 90 $18. 00 125 $19. 15 $18. 75 130 $19. 40 $19. 50 135 $19. 65 $20. 25 y = 12. 90 + 0. 05 x y = 0. 15 x 12. 90 + 0. 05 x = 0. 15 x – 0. 05 x 12. 90 = 0. 10 x 0. 10 129 min. = x

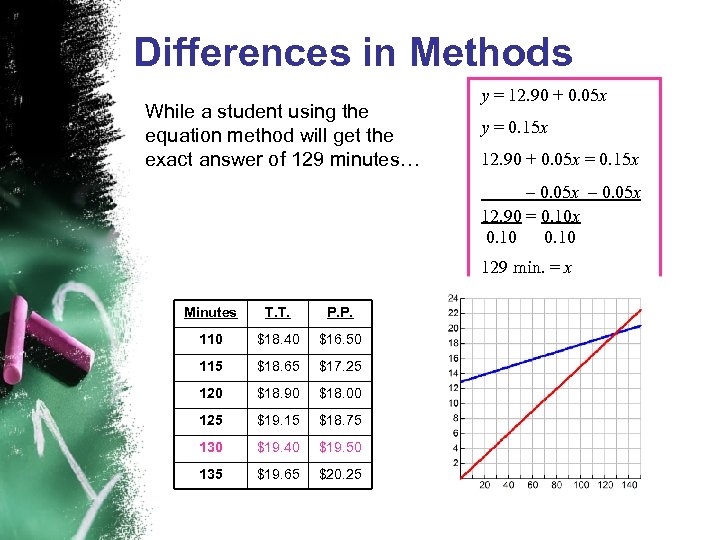
Differences in Methods While a student using the equation method will get the exact answer of 129 minutes… y = 12. 90 + 0. 05 x y = 0. 15 x 12. 90 + 0. 05 x = 0. 15 x – 0. 05 x 12. 90 = 0. 10 x 0. 10 129 min. = x Minutes T. T. P. P. 110 $18. 40 $16. 50 115 $18. 65 $17. 25 120 $18. 90 $18. 00 125 $19. 15 $18. 75 130 $19. 40 $19. 50 135 $19. 65 $20. 25

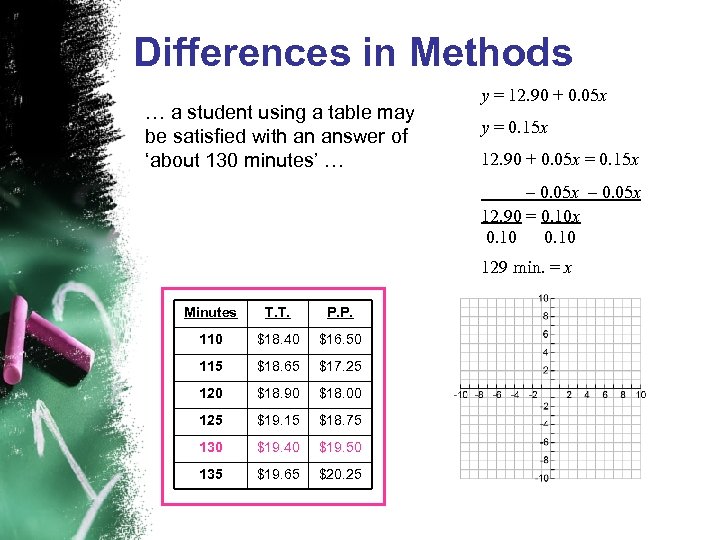
Differences in Methods … a student using a table may be satisfied with an answer of ‘about 130 minutes’ … y = 12. 90 + 0. 05 x y = 0. 15 x 12. 90 + 0. 05 x = 0. 15 x – 0. 05 x 12. 90 = 0. 10 x 0. 10 129 min. = x Minutes T. T. P. P. 110 $18. 40 $16. 50 115 $18. 65 $17. 25 120 $18. 90 $18. 00 125 $19. 15 $18. 75 130 $19. 40 $19. 50 135 $19. 65 $20. 25

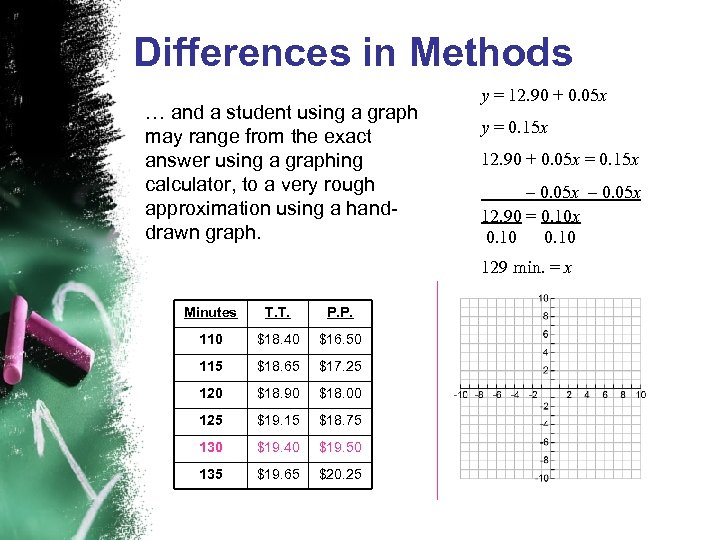
Differences in Methods … and a student using a graph may range from the exact answer using a graphing calculator, to a very rough approximation using a handdrawn graph. y = 12. 90 + 0. 05 x y = 0. 15 x 12. 90 + 0. 05 x = 0. 15 x – 0. 05 x 12. 90 = 0. 10 x 0. 10 129 min. = x Minutes T. T. P. P. 110 $18. 40 $16. 50 115 $18. 65 $17. 25 120 $18. 90 $18. 00 125 $19. 15 $18. 75 130 $19. 40 $19. 50 135 $19. 65 $20. 25

Differences in Methods Take advantage of opportunities such as this to discuss real-life situations where it’s important to be exact, and others where ‘close’ might be good enough. y = 12. 90 + 0. 05 x y = 0. 15 x 12. 90 + 0. 05 x = 0. 15 x – 0. 05 x 12. 90 = 0. 10 x 0. 10 129 min. = x Minutes T. T. P. P. 110 $18. 40 $16. 50 115 $18. 65 $17. 25 120 $18. 90 $18. 00 125 $19. 15 $18. 75 130 $19. 40 $19. 50 135 $19. 65 $20. 25

Step 5: REFLECT Each person should reflect on the processes used, addressing questions such as: • What methods did you use in the solution? • Why did you use those methods? • If you were to approach a similar problem tomorrow, what would you do differently? The same? Why? • How will you approach the next problem you have in class, based on this experience?

Step 5: REFLECT If students did not get the correct answer, they should be encouraged to reflect in writing what they did wrong. This will lead to enhanced metacognition. (See Power. Point lesson on “Developing Thinking Skills”)

TRANSFER Finally, as a group, discuss the question: “Where else in life are these general strategies useful? ”

Applying Best Practices • Think of a concept you will be teaching in your class in the near future. • Develop a lesson plan incorporating the steps discussed here: - Identify the Problem - Select a Solution Path - Carry Out the Plan - Check the Answer - REFLECT

What About TIME? Many resources are available to assist in developing TRUE problemsolving skills, providing deep, engaging problems as well as guiding students through their own thinking process.

What About TIME? Browse through what’s available through NCTM. (www. nctm. org) When looking for math textbooks, watch for products that encourage TRUE problem-solving rather than drill-and-practice.

What About TIME? For curriculum ideas and other support for both mathematics and science teaching, check out www. project 2061. org Don’t feel bound to a textbook, but use it to your advantage. Many times you can take existing problems and rework them to encourage TRUE problem-solving.