Probability Theory Instructor Assoc Prof Dr Deshi Ye

Probability Theory Instructor: Assoc. Prof. Dr. Deshi Ye ( 叶德仕 ) College of Computer Science Zhejiang University Email: yedeshi@zju. edu. cn Course homepage: Http: //www. cs. zju. edu. cn/people/yedeshi/prob 12/

Outline o Brief introduction to the course n Syllabus, course policies and contents o Introduction to probability and statistics n History and importance o Treatment of data n Graphs: Pareto Diagram, Dot Diagram, Box-plot n Frequency distribution, Stem-and-leaf Displays

Course information o What is for? n This course provides an elementary introduction to probability with applications. n Topics include: o axioms of probability; o basic probability concepts and models (counting methods , conditional probability, Bayes theorem, et. ); o random variables; independence; o discrete and continuous probability distributions; o calculate mathematical expectation and variance; o limit theory

Course Goals o Students at the end of course should be able to do the following: n 1) Understand the concepts and methods of probability theory n 2) Contrast, evaluate, and implement simulations or experiments n 3) Utilize Minitab program for analyzing data and summarizing

Syllabus o Prerequisite: one year course in calculus o Textbooks (required): Miller & Freund's Probability and Statistics for Engineers (Seventh Edition), Richard A. Johnson. Publishing House of Electronics Industry or Pearson Education Press. o Chapter 1 -6 for “Probability Theory”, Chapter 7 -13 for the second semester (“Mathematical Statistics”). o References: 1) A First course in Probability (6 th Ed), Sheldon Ross. China Statistics Press. 2) Probability & Statistics for Engineers & Scientists (7 th Ed), R. E. Walpole, R. H. Myers, S. L. Myers, K. Ye. Tshinghua or Pearson Education Press.

Grading o Grades for the course will be based on the following weighting 1) Class attendance and Homework assignment: 36% 2) Unit quiz: 24% (12%, 12%) 3) Final exam: 40%

Homework o 1) You may collaborate on homework, but you must write your submitted work in your own words. All steps are required, this includes showing calculations, derivations, and proofs. Solutions will be posted on the class web site. o 2)Assignments are due in class as noted in the syllabus and web page.

Checking web page o I am highly recommend that each student check this web page at least once a week for new announcements and homework assignments. http: //www. cs. zju. edu. cn/people/yedeshi/software/Mini. TAB 14. iso

Probability in CS o Randomized algorithms o Querying Theory o Software testing o Computer simulation and modeling

Introduction o Probability theory is devoted to the study of uncertainty and variability n Probability quantifies how uncertain we are about future events o Statistics can be described as the study of how to make inference and decisions in the face of uncertainty and variability

Uncertainty Events o o o Say red Coin toss Matching games (Cards, Name) Traffic light The life of a light Lotteries?

Poker Lotteries o http: //www. zjlottery. com/news/showmes. a sp? newsid=9950 o Heart, Spade, Club, Diamonds o 1（A）、2、3、4、5、6、7、8、9、10、11（ J）、12（Q）、13（K） o Arbitrarily choose one piece o cost 2￥，if win you are awarded 13￥ (win in 1/13)

Why measure uncertainty? o To make tradeoffs among uncertain events o Measure combined effect of several uncertain events o To communicate about uncertainty

Brief History o Blaise Pascal and Pierre de Fermat: the origins of probability are found. n concerning a popular dice game n fundamental principles of probability theory o Pierre de Laplace: n Before him, concern on the analysis of games of chance n Laplace applied probabilistic ideas to many scientific and practical problems

History cont. o Mathematical statistics is one important branch of applied probability; other applications occur in such widely different fields as genetics, psychology, economics, engineering, computer science. o Important workers: Chebyshev, Markov, von Mises, and Kolmogorov o One of the difficulties is the definition of probability. 20 th century, it was solved by treating probability theory on an axiomatic basis (Kolmogorov).

Words for probability o Chance: the falling out or happening of events o Stochastic: randomly determined o Random: not sent or guided in a special direction, having no definite aim or purpose o Aleatory: dependent on the throw of a die o Hazard: a chance or venture.

Importance of Prob. Theory o Two major applications of Prob. n Risk assessment (new medical treatments) n Reliability (weather prediction, earthquake, reduce failure of consumer product) o Why statistics and probability in engineering? n Quantify the uncertainty associated with engineer model n Evaluate the result of experiment n Assess importance of measurement uncertainty n Safeguard for persons, qualities of environment, assets

A case study o Visually inspecting data to improve product quality o Monitoring manufacturing data o Ceramic part in coffee makers, which is made by filling the mixture of clay-water-oil. The depth of the slot is uncontrolled. o Slot depth was measured on three ceramic parts selected from production every half hour during the first 6 AM to 3 PM.

Time series plot Stable: 217. 5 Good quality: [215, 220]

Ch 2: Treatment of data o Outline n n n Pareto diagrams, dot diagrams Histograms (Frequency distributions) Stem-and-leaf display Box-plot (Quartiles and Percentiles) The calculation of mean and standard deviation s

What it is – Descriptive statistics o Descriptive statistics include the numbers, tables, charts, and graphs used to describe, organize, summarize, and present raw data. n n central tendency (location) of data, i. e. where data tend to fall, as measured by the mean, median, and mode. dispersion (variability) of data, i. e. how spread out data are, as measured by the variance and its square root, the standard deviation. skew (symmetry) of data, i. e. how concentrated data are at the low or high end of the scale, as measured by the skew index. kurtosis (peakedness) of data, i. e. how concentrated data are around a single value, as measured by the kurtosis index.

Pareto Diagram o Pareto Diagram display orders each type of failure or defect according to its frequency. o For a computer-controlled lathe whose performance was below par, workers recorded the following causes and their frequencies: power fluctuations 6 controller not stable 22 operator error 13 worn tool not replaced 2 other 5

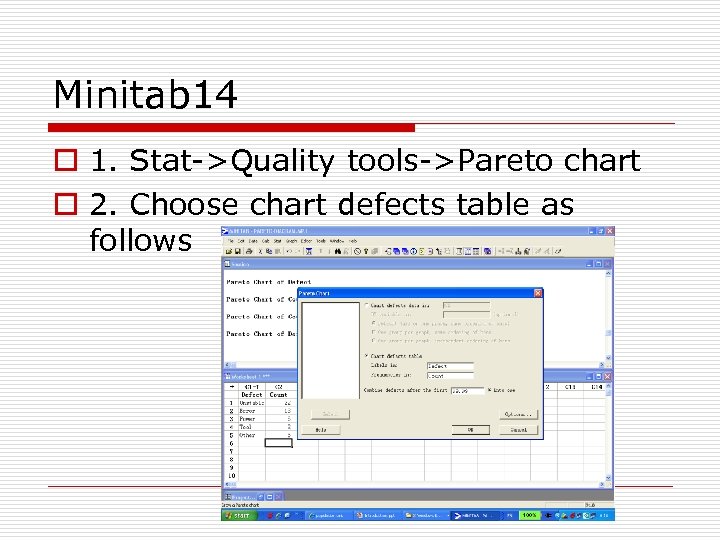
Minitab 14 o 1. Stat->Quality tools->Pareto chart o 2. Choose chart defects table as follows

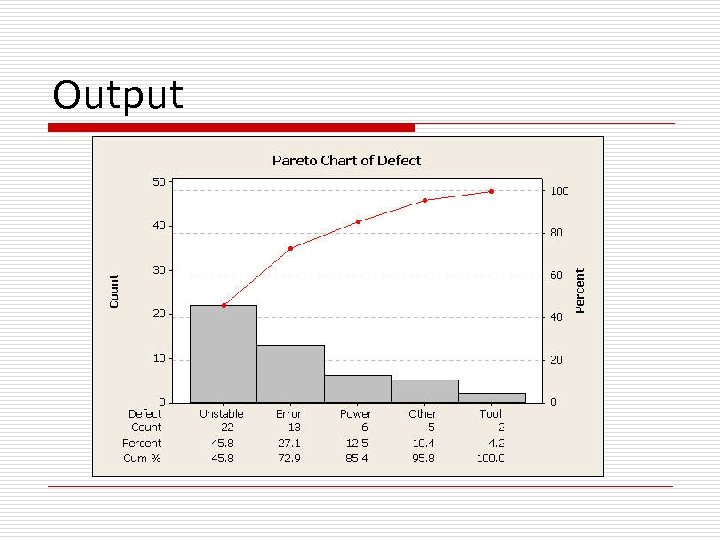
Output

Pareto diagram o Pareto diagram: depicts Pareto’s empirical law that any assortment of events consists of a few major and many minor elements. o Typically, two or three elements will account for more than half of the total frequency, i. e. , it points out the main causes.

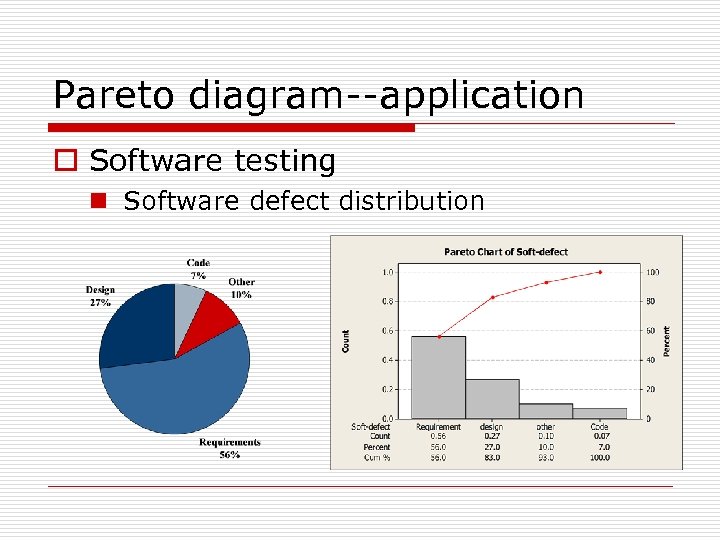
Pareto diagram--application o Software testing n Software defect distribution

Dot diagram o Second step to improve the quality of lathe, o Data were collected from observation on the deviations of cutting speed from the target value set by the controller. o EX. Cutting speed – target speed o 3 6 – 2 4 7 4 o Dot diagram: A number line in which one dot is placed above a value on the number line for each occurrence of that value. That is, one dot means the value occurred once, three dots mean the value occurred three times, etc. o In minitab: stat->dotplots->simple

Dot diagram o This diagram visually summarize the information that the lathe is generally running fast.

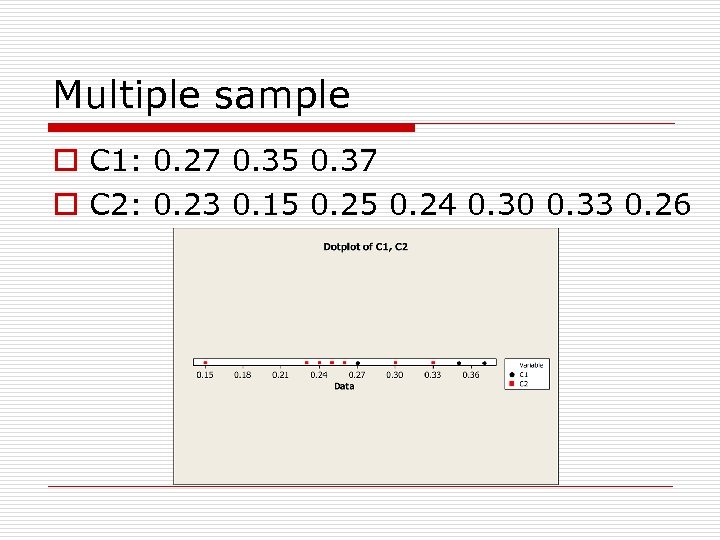
Multiple sample o C 1: 0. 27 0. 35 0. 37 o C 2: 0. 23 0. 15 0. 24 0. 30 0. 33 0. 26

Frequency distributions o A frequency distribution is a tabular arrangement of data whereby the data is grouped into different intervals, and then the number of observations that belong to each interval is determined. o Data that is presented in this manner are known as grouped data.

Data 001. 80 data of emission (in ton)of sulfur oxides from an industry plant o 15. 8 26. 4 17. 3 11. 2 23. 9 24. 8 18. 7 13. 9 9. 0 13. 2 22. 7 9. 8 6. 2 14. 7 17. 5 26. 1 12. 8 28. 6 17. 6 23. 7 26. 8 o 22. 7 18. 0 20. 5 11. 0 20. 9 15. 5 19. 4 16. 7 10. 7 19. 1 15. 2 22. 9 26. 6 20. 4 21. 4 19. 2 21. 6 16. 9 19. 0 18. 5 23. 0 o 24. 6 20. 1 16. 2 18. 0 7. 7 13. 5 23. 5 14. 4 29. 6 19. 4 17. 0 20. 8 24. 3 22. 5 24. 6 18. 4 18. 1 8. 3 21. 9 12. 3 o 22. 3 13. 3 11. 8 19. 3 20. 0 25. 7 31. 8 25. 9 10. 5 15. 9 27. 5 18. 1 17. 9 9. 4 24. 1 20. 1 28. 5

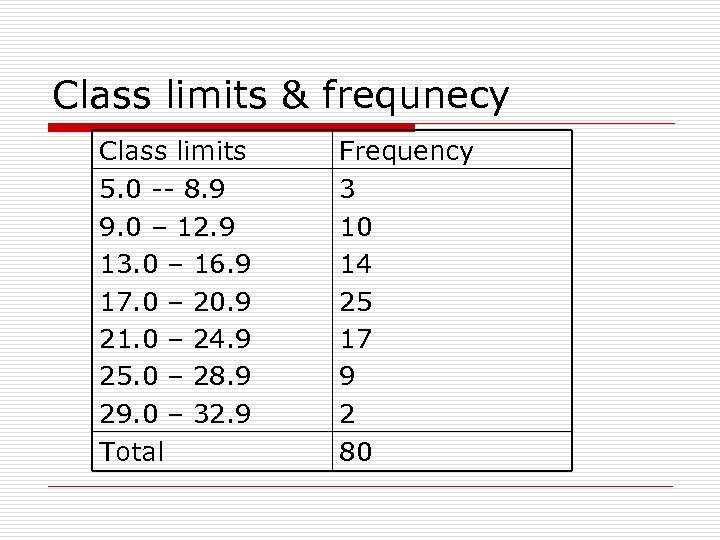
Class limits & frequnecy Class limits 5. 0 -- 8. 9 9. 0 – 12. 9 13. 0 – 16. 9 17. 0 – 20. 9 21. 0 – 24. 9 25. 0 – 28. 9 29. 0 – 32. 9 Total Frequency 3 10 14 25 17 9 2 80

Class limit and width o lower class limit: The smallest value that can belong to a given interval o upper class limit: The largest value that can belong to the interval. o Class width: The difference between the upper class limit and the lower class limit is defined to be the class width.

Guidelines for classes o o o 1. There should be between 5 and 20 classes. 2. The class width should be an odd number. This will guarantee that the class midpoints are integers instead of decimals. 3. The classes must be mutually exclusive. This means that no data value can fall into two different classes 4. The classes must be all inclusive or exhaustive. This means that all data values must be included. 5. The classes must be continuous. There are no gaps in a frequency distribution. Classes that have no values in them must be included (unless it's the first or last class which are dropped). 6. The classes must be equal in width. The exception here is the first or last class. It is possible to have an "below. . . " or ". . . and above" class. This is often used with ages

Steps o 1. Find the largest and smallest values o 2. Compute the Range = Maximum - Minimum o 3. Select the number of classes desired. This is usually between 5 and 20. o 4. Find the class width by dividing the range by the number of classes and rounding up. You must round up, not off. Normally 3. 2 would round to be 3, but in rounding up, it becomes 4.

Class limits & frequnecy Class limits [5. 0, 9. 0) [9. 0, 13. 0) [13. 0, 17. 0) [17. 0, 21. 0) [21. 0, 25. 0) [25. 0, 29. 0) [29. 0, 33. 0) Total Frequency 3 10 14 25 17 9 2 80

Variants of frequency distribution o The cumulative frequency distribution is obtained by computing the cumulative frequency, defined as the total frequency of all values less than the upper class limit of a particular interval, for all intervals. o Relative frequency: the ratio of the number of observations in the interval to the total number of observations o The percentage frequency distribution is arrived at by multiplying the relative frequencies of each interval by 100%.

Cumulative frequency Class limits Less than 5 Less than 9 Less than 13 Less than 17 Less than 21 Less than 25 Less than 29 Less than 33 Frequency 0 3 13 27 52 69 78 80

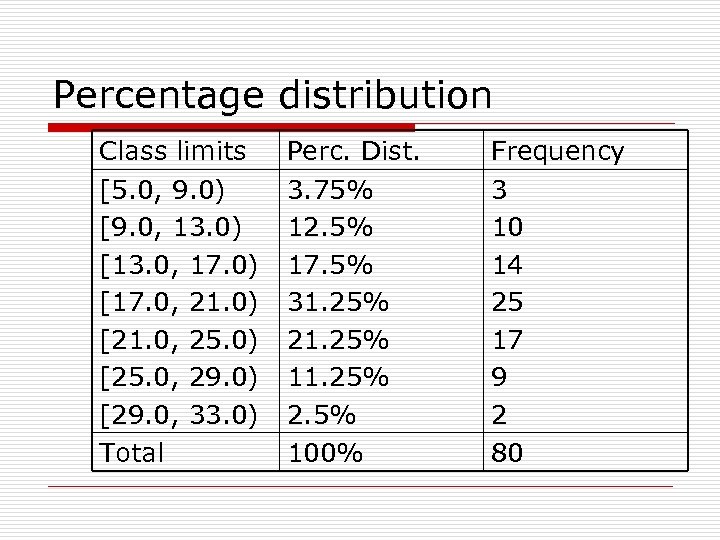
Percentage distribution Class limits Perc. Dist. Frequency [5. 0, 9. 0) [9. 0, 13. 0) [13. 0, 17. 0) [17. 0, 21. 0) [21. 0, 25. 0) [25. 0, 29. 0) [29. 0, 33. 0) Total 3. 75% 12. 5% 17. 5% 31. 25% 21. 25% 11. 25% 2. 5% 100% 3 10 14 25 17 9 2 80

Histogram o The most common form of graphical presentation of a frequency distribution is the histogram. o Histogram: is constructed of adjacent rectangles; the height of the rectangles is the class frequencies and the bases of the rectangles extend between successive class boundaries.

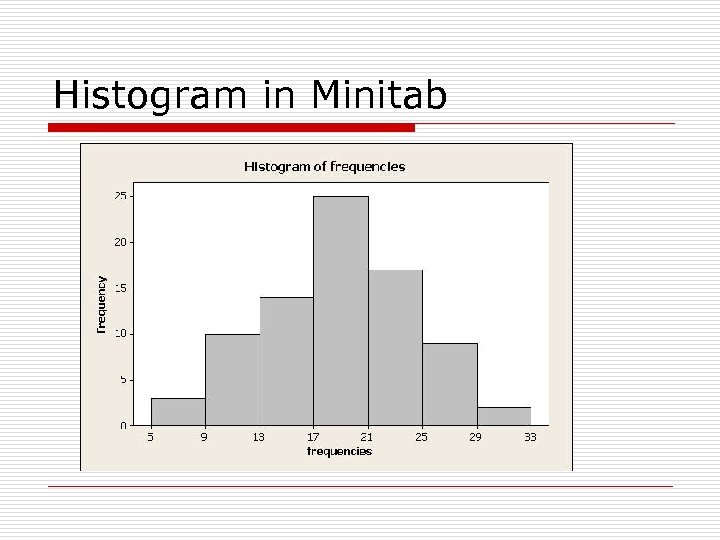
Histogram in Minitab

Histogram in Minitab 1. Graph->histogram->simple 2. Graph variables: c 4 (all data in a column) 3. Edit bars: Click the bars in the output figures, in Binning, Interval type select midpoint and interval definition select midpoint/cutpoint, and then input 7 11 15 19 23 27 31 as illustrated in the following

Density histogram o When a histogram is constructed from a frequency table having classes of unequal lengths, the height of each rectangle must be changed to o Height = relative frequency / width. o The area of the rectangle then represents the relative frequency for the class and the total area of the histogram is 1.

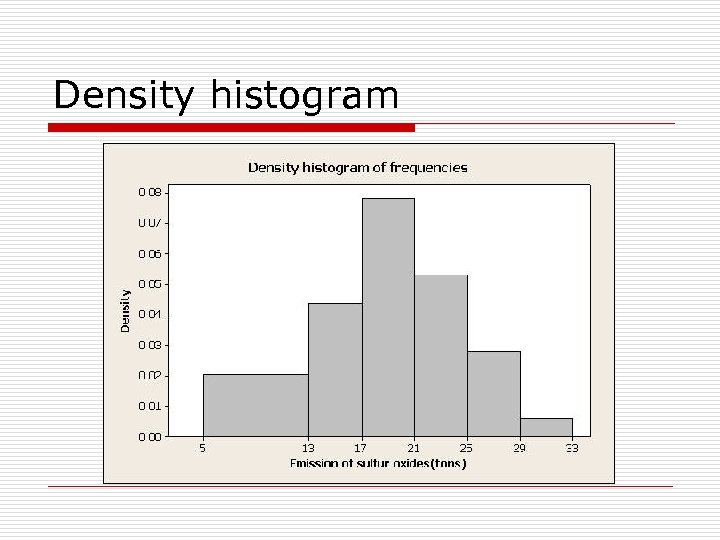
Density histogram

Density Histogram o o Graph->histogram->simple Scale->Y-Scale Type->Density Edit Bars->Binning->Cut point-> 5 13 17 21 25 29 33

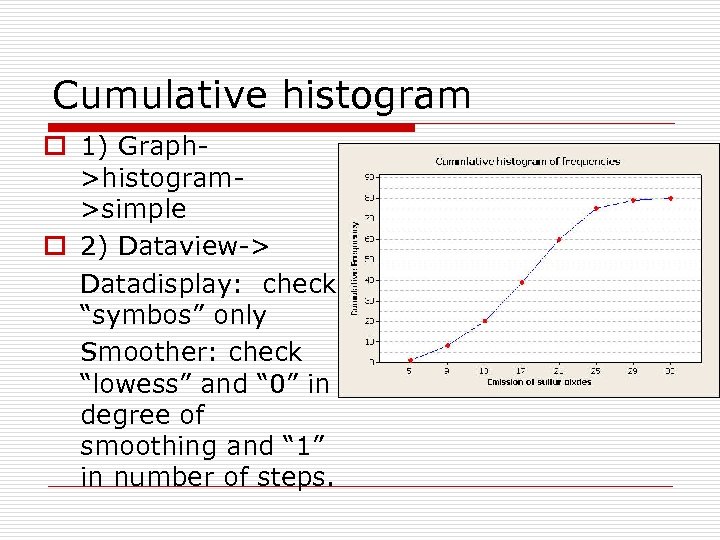
Cumulative histogram o 1) Graph>histogram>simple o 2) Dataview-> Datadisplay: check “symbos” only Smoother: check “lowess” and “ 0” in degree of smoothing and “ 1” in number of steps.

Stem-and-leaf Display o Class limits and frequency, contain data in each class, but the original data points have been lost. o Stem-and-leaf: A data plot which uses part of the data value as the stem and the rest of the data value (the leaf) to form groups or classes. This is very useful for sorting data quickly. o Stem-and-leaf: function the same as histogram but save the original data points. o Example: 11 numbers: o 12, 13, 21, 27, 33, 34, 35, 37, 40, 41

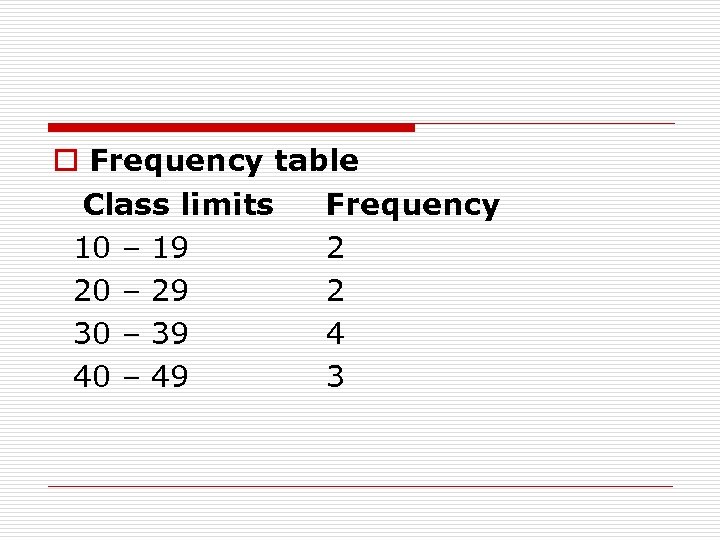
o Frequency table Class limits Frequency 10 – 19 2 20 – 29 2 30 – 39 4 40 – 49 3

Stem-and-leaf: each row has a stem and each digit on a stem to the right of the vertical line is a life. The "stem" is the left-hand column which contains the tens digits. The "leaves" are the lists in the right-hand column, showing all the ones digits for each of the tens, twenties, thirties, and forties. Key: “ 4|0” means 40

Stem-and-leaf Display o Example in P 23: 20 numbers: o 29, 44, 12, 53, 21, 34, 39, 25, 48, 23 o 17, 24, 27, 32, 34, 15, 42, 21, 28, 27 Frequency table Class limits Frequency 10 – 19 3 20 – 29 9 30 – 39 4 Stem-and-leaf 40 – 49 3 1|257 50 – 59 1 2|113457789 3|244 9 4|248 5|3

Stem-and-leaf in Minitab o The display has three columns: n The leaves (right) - Each value in the leaf column represents a digit from one observation. n The stem (middle) - The stem value represents the digit immediately to the left of the leaf digit. n Counts (left) - If the median value for the sample is included in a row, the count for that row is enclosed in parentheses. The values for rows above and below the median are cumulative.

Stem-and-leaf for DATA 001 o o Stem-and-leaf of frequencies N = 80 Leaf Unit = 1. 0 o o o o 2 0 67 6 0 8999 11 1 00111 17 1 223333 24 1 4445555 32 1 66677777 (13) 1 8888888999999 35 2 0000000111 25 2 222223333 16 2 4444455 9 2 66667 4 2 889 1 3 1

Ch 2. 5: Descriptive measures o Mean: the sum of the observation divided by the sample size. o Median: the center, or location, of a set of data. If the observations are arranged in an ascending or descending order: n If the number of observations is odd, the median is the middle value. n If the number of observations is even, the median is the average of the two middle values.

Example o 15 14 2 27 13 o Mean: o Ordering the data from smallest to largest n 2 13 14 15 27 o The median is the third largest value 14

Other central tendency o Midrange n The midrange is simply the midpoint between the highest and lowest values. o Mode n The mode is the most frequent data value. There may be no mode if no one value appears more than any other. There may also be two modes (bimodal), three modes (trimodal), or more than three modes (multi-modal).

Summary o The Mean is used in computing other statistics (such as the variance) and does not exist for open ended grouped frequency distributions. It is often not appropriate for skewed distributions such as salary information. o The Median is the center number and is good for skewed distributions because it is resistant to change. o The Mode is used to describe the most typical case. The mode can be used with nominal data whereas the others can't. The mode may or may not exist and there may be more than one value for the mode o The Midrange is not used very often. It is a very rough estimate of the average and is greatly affected by extreme values (even more so than the mean).

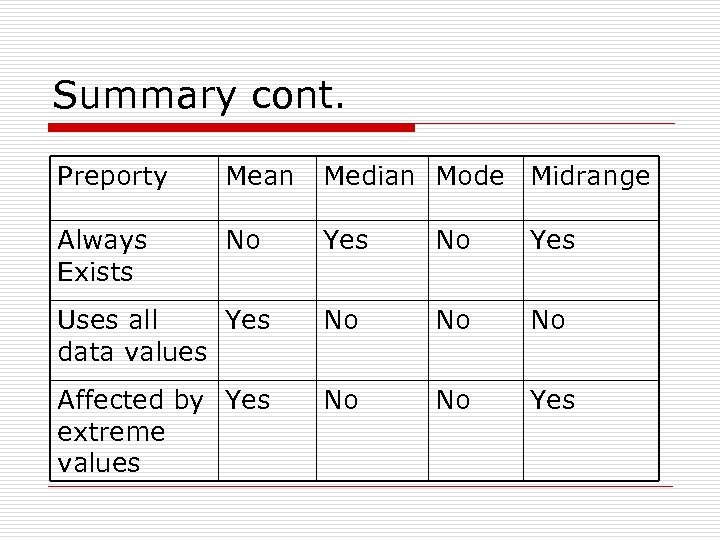
Summary cont. Preporty Mean Median Mode Midrange Always Exists No Yes Uses all Yes data values No No No Affected by Yes extreme values No No Yes

Sample variance o Deviations from the mean: o Standard deviation s:

Quartiles and Percentiles o Quartiles: are values in a given set of observations that divide the data in 4 equal parts. o The first quartile, , is a value that has one fourth, or 25%, of the observation below its value. o The sample 100 p-th percentile is a value such that at least 100 p% of the observation are at or below this value, and at least 100(1 -p)% are at or above this value.

Example o Example in P 34: N/4 is an integer, take the average; Or round up, otherwise

Boxplots o A boxplot is a way of summarizing information contained in the quartiles (or on a interval) o Box length= interquartile range=

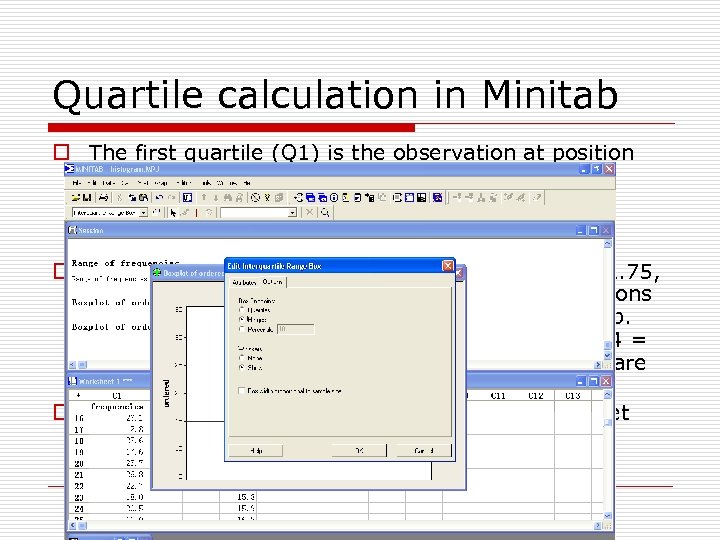
Quartile calculation in Minitab o The first quartile (Q 1) is the observation at position (n+1) / 4, and the third quartile (Q 3) is the observation at position 3(n+1) / 4, where n is the number of observations. If the position is not an integer, interpolation is used. o For example, suppose n=10. Then (10 + 1)/4 = 2. 75, and Q 1 is between the second and third observations (call them x 2 and x 3), three-fourths of the way up. Thus, Q 1 = x 2 + 0. 75(x 3 - x 2). Since 3(10 + 1)/4 = 8. 25, Q 3 = x 8 + 0. 25(x 9 - x 8), where x 8 and x 9 are the eight and ninth observations. o Indeed, Choose “Hinges” in Box. Endpoints, will get Quartile as in Textbook.

Modified boxplot Upper limit = Q 3 + 1. 5 (Q 3 - Q 1) o Outlier: too far from third quartile. o Largest observation within 1. 5(interquartile range) of third quartile. o Modified boxplot: identify outliers and reduce the effect on the shape of the boxplot. Lower limit = Q 1 - 1. 5 (Q 3 - Q 1)

Homework 1 o Problems in Textbook (2. 62, 2. 67, 2. 71, 2. 72, 2. 75) 4 points o Due date: next lecture.

Conclusion o Graph the data as a dot diagram or histogram or box plot to assess the overall pattern of data o Group the data by frequency distribution, Stem-and-leaf o Calculate the summary statisticssample mean, standard deviation, and quartiles – to describe the data set.

The END Thanks !