Probability & Sample Space
Probability The probability of a number is a ratio that compares the number of successes to the total possible outcomes.
Probability Probabilities can be expressed as a fraction, a decimal, or a percent. 0% 50% 100% 0 Impossible 1/2 1 Certain
Probability Something that will never happen has a 0% probability. Exmaple: There is a 0% probability that humans will be able to breath underwater (without an oxygen mask). 0% 50% 0 Impossible 100% 1/2 1 Certain
Probability Something that will always happen has a 100% probability. Example: There is a 100% probability that water will freeze At 32 degrees Fahrenheit. 0% 50% 100% 0 Impossible 1/2 1 Certain
Sample Space In order to determine the probability of an event occurring, you must first determine the sample space. The sample space of an event is all possible outcomes.
Example 1 Suppose your favorite color is teal. If you were going to close your eyes and choose a balloon at random, what is the probability that you would choose your favorite color?
Example 1 First we must determine the sample space: There are four possible outcomes: you could grab the peach one, the purple one, the pink one, or the teal one.
Example 1 The sample space is all possible outcomes: Peach Purple Pink Teal
Example 1 The probability of grabbing the teal balloon is the number of teal balloons, 1, divided by the number of possible outcomes, 4. P(teal) =
Example 1 We can also find the probabilities for the other colors. P(peach) = P(purple) = P(pink) =
Example 2 You are playing a game that involves one die. What is the probability of rolling a 6? First we must determine the sample space.
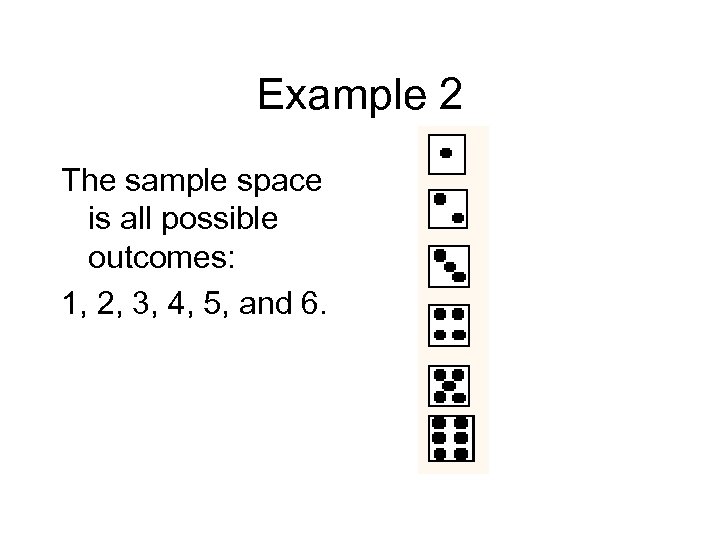
Example 2 The sample space is all possible outcomes: 1, 2, 3, 4, 5, and 6.
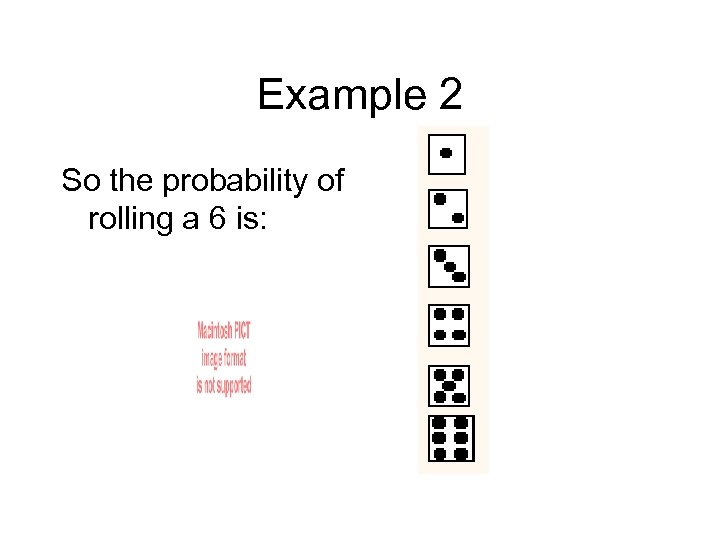
Example 2 So the probability of rolling a 6 is:
Example 3 Suppose you were going to roll a tetrahedral die. What is the probability of rolling a 1? Sample Space: 1, 2, 3, 4
Example 3 Since there are only four outcomes, the The probability of rolling a 1 is:
Example 4 Suppose you were going to toss two coins. What is the sample space? HH HT TH TT
Example 4 What is the probability of tossing two heads? HH HT TH TT
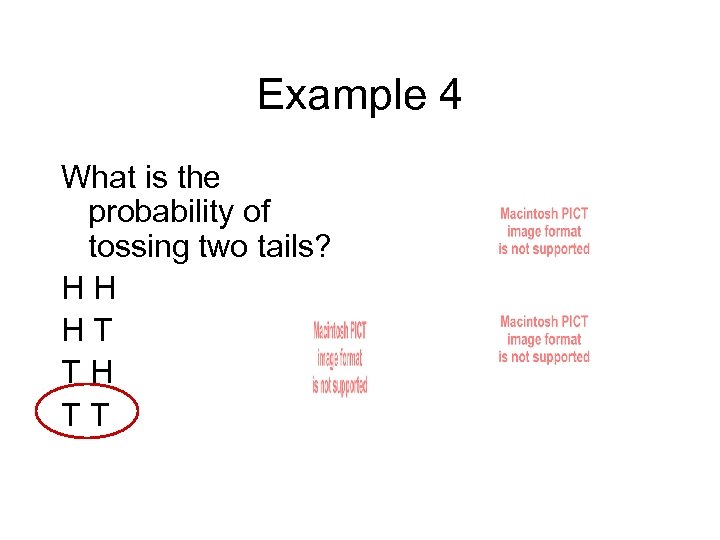
Example 4 What is the probability of tossing two tails? HH HT TH TT
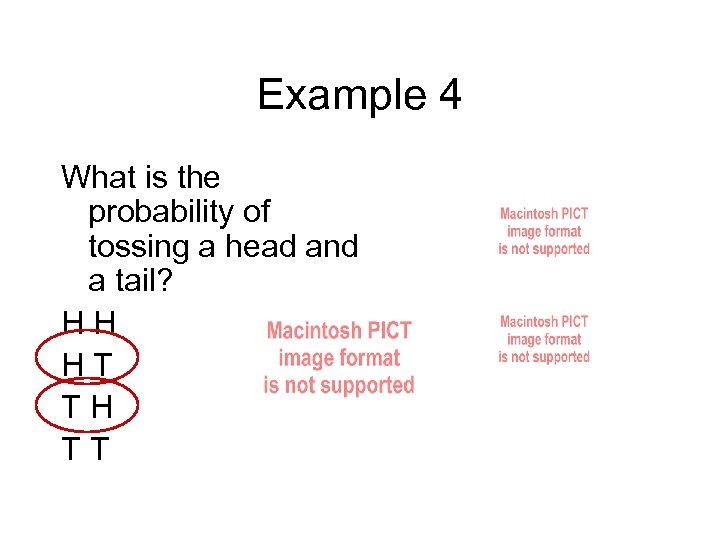
Example 4 What is the probability of tossing a head and a tail? HH HT TH TT
Example 5 You are playing a game that involves 2 dice. What is the sample space?
Example 5 On the first die, we can get a 1, 2, 3, 4, 5, or 6. On the second die, we can get a 1, 2, 3, 4, 5, or 6.
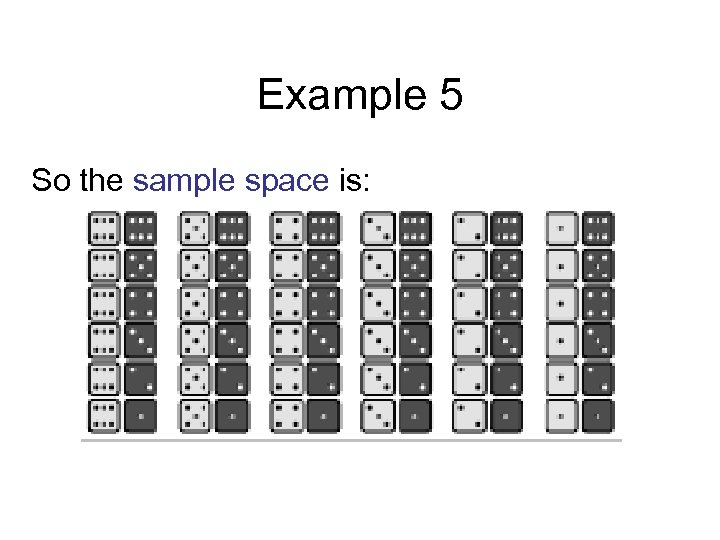
Example 5 So the sample space is:
Example 5 Since there were six possible numbers we could roll for the first die, and six possible numbers we could roll for the second die, there a total of 6 x 6 = 36 possible combinations!
Example 6 You are going to buy a pizza. The pizzas come in three different sizes with three choices of seasoning. Size Seasoning Small Pepper Medium Basil Large Onions
Example 6 What is the sample space? Let’s use a counting tree to help us determine all the possible pizzas we can create!
Example 6 So the sample space is: Small + Pepper Small + Basil Small + Onion Medium + Pepper Medium + Basil Medium + Onion Large + Pepper Large + Basil Large + Onion There were 3 choices for the size, and 3 choices for the seasoning. So there a total of 3 x 3 = 9 possible combinations!
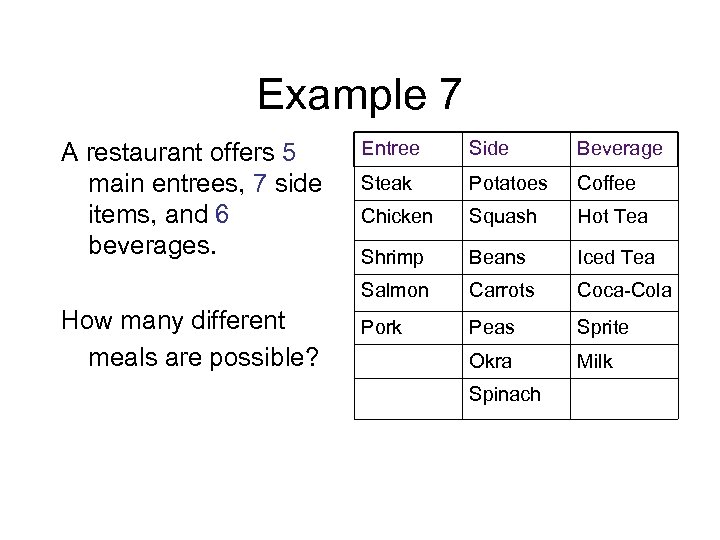
Example 7 How many different meals are possible? Entree Side Beverage Steak Potatoes Coffee Chicken Squash Hot Tea Shrimp Beans Iced Tea Salmon A restaurant offers 5 main entrees, 7 side items, and 6 beverages. Carrots Coca-Cola Pork Peas Sprite Okra Milk Spinach
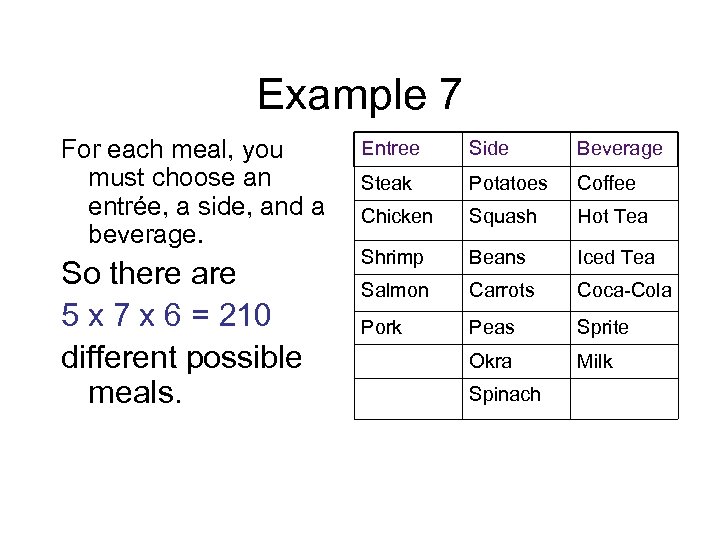
Example 7 For each meal, you must choose an entrée, a side, and a beverage. So there are 5 x 7 x 6 = 210 different possible meals. Entree Side Beverage Steak Potatoes Coffee Chicken Squash Hot Tea Shrimp Beans Iced Tea Salmon Carrots Coca-Cola Pork Peas Sprite Okra Milk Spinach
Скачать презентацию Probability Sample Space Probability The probability
1df95009fd11a2d18bc1cc4381dd7815.ppt