efd9ff5203f3f032d089a68f4475cc2d.ppt
- Количество слайдов: 21

Probabilistic Time Estimates • Reflect uncertainty of activity times • Beta distribution is used in PERT Mean (expected time): t = a + 4 m + b 6 2 b-a Variance: 2 =( ) 6 Where, a = optimistic estimate m = most likely time estimate b = pessimistic time estimate © 2000 by Prentice-Hall Inc Russell/Taylor Oper Mgt 3/e Ch 17 - 23
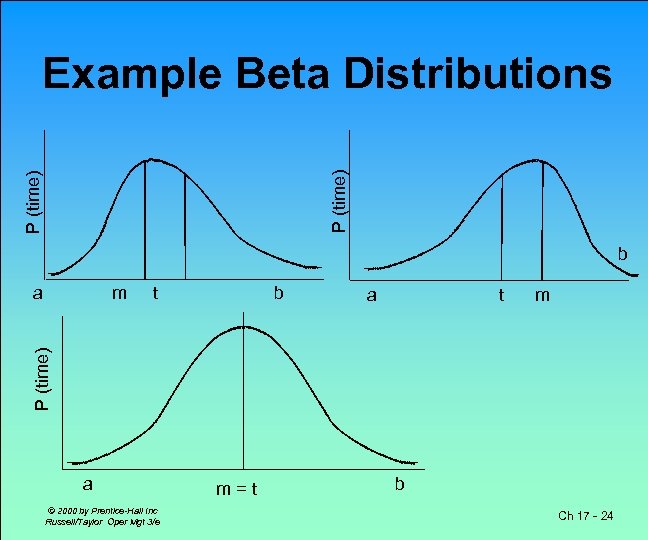
P (time) Example Beta Distributions b a b t a t m P (time) m a © 2000 by Prentice-Hall Inc Russell/Taylor Oper Mgt 3/e m=t b Ch 17 - 24
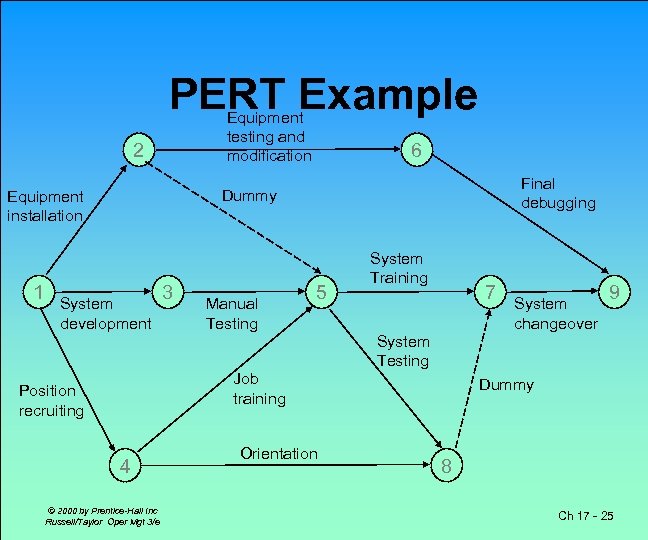
PERT Example Equipment testing and modification 2 Final debugging Dummy Equipment installation 1 6 System development 3 Manual Testing 5 System Training 7 System changeover 9 System Testing Job training Position recruiting 4 © 2000 by Prentice-Hall Inc Russell/Taylor Oper Mgt 3/e Orientation Dummy 8 Ch 17 - 25
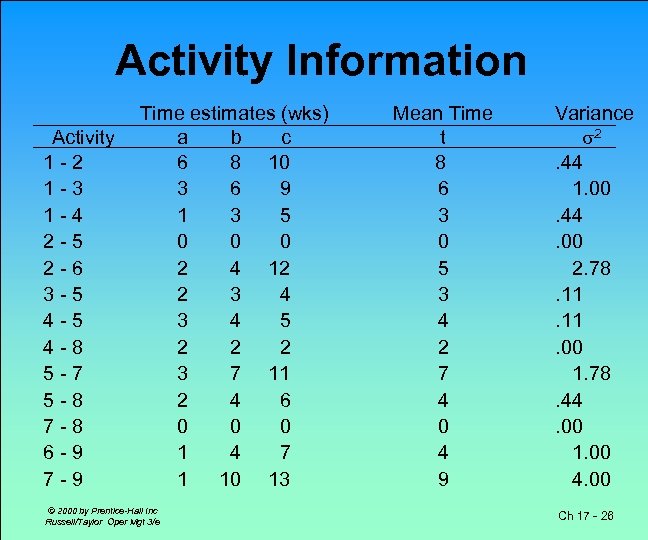
Activity Information Activity 1 -2 1 -3 1 -4 2 -5 2 -6 3 -5 4 -8 5 -7 5 -8 7 -8 6 -9 7 -9 Time estimates (wks) a b c 6 8 10 3 6 9 1 3 5 0 0 0 2 4 12 2 3 4 5 2 2 2 3 7 11 2 4 6 0 0 0 1 4 7 1 10 13 © 2000 by Prentice-Hall Inc Russell/Taylor Oper Mgt 3/e Mean Time t 8 6 3 0 5 3 4 2 7 4 0 4 9 Variance 2. 44 1. 00. 44. 00 2. 78. 11. 00 1. 78. 44. 00 1. 00 4. 00 Ch 17 - 26
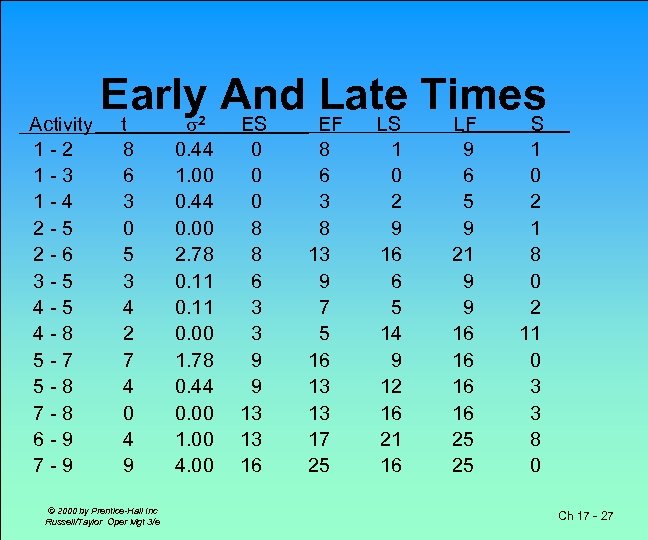
Activity 1 -2 1 -3 1 -4 2 -5 2 -6 3 -5 4 -8 5 -7 5 -8 7 -8 6 -9 7 -9 Early And Late Times t 8 6 3 0 5 3 4 2 7 4 0 4 9 © 2000 by Prentice-Hall Inc Russell/Taylor Oper Mgt 3/e 2 0. 44 1. 00 0. 44 0. 00 2. 78 0. 11 0. 00 1. 78 0. 44 0. 00 1. 00 4. 00 ES 0 0 0 8 8 6 3 3 9 9 13 13 16 EF 8 6 3 8 13 9 7 5 16 13 13 17 25 LS 1 0 2 9 16 6 5 14 9 12 16 21 16 LF 9 6 5 9 21 9 9 16 16 25 25 S 1 0 2 1 8 0 2 11 0 3 3 8 0 Ch 17 - 27
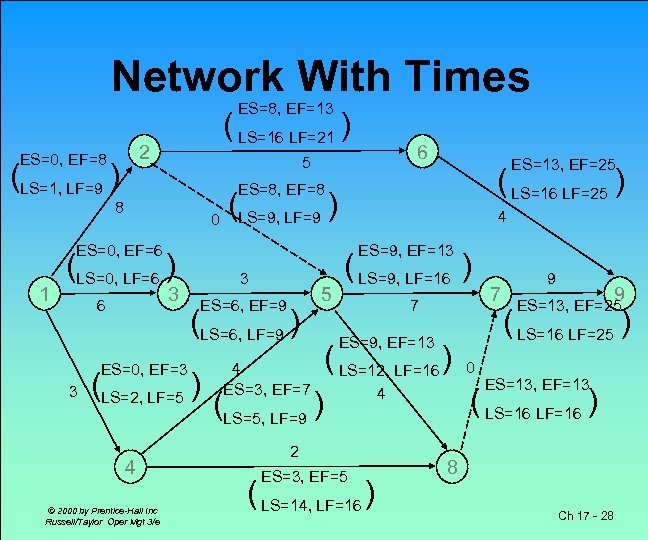
Network With Times ES=8, EF=13 ( LS=16 LF=21 ) 2 ES=0, EF=8 (LS=1, LF=9 ) 0 ( LS=16 LF=25 ) (LS=9, LF=9 ) ES=0, EF=6 3 6 ES=0, EF=3 3 ES=6, EF=9 (LS=6, LF=9 ) (LS=2, LF=5 ) 4 © 2000 by Prentice-Hall Inc Russell/Taylor Oper Mgt 3/e 4 ES=9, EF=13 (LS=0, LF=6 ) 3 ES=13, EF=25 ES=8, EF=8 8 1 6 5 4 ES=3, EF=7 5 ( LS=9, LF=16 ) 7 ES=9, EF=13 ( LS=12, LF=16 ) (LS=5, LF=9 ) 2 ES=3, EF=5 ( LS=14, LF=16 ) 0 7 9 9 ES=13, EF=25 ( LS=16 LF=25 ) ES=13, EF=13 ( LS=16 LF=16 ) 4 8 Ch 17 - 28

Project Variance • Project variance is the sum of variances on the critical path © 2000 by Prentice-Hall Inc Russell/Taylor Oper Mgt 3/e Ch 17 - 29

Probabilistic Network Analysis Determine probability that project is completed within specified time Z= x- where = tp = project mean time = project standard deviation x = proposed project time Z = number of standard deviations x is from mean © 2000 by Prentice-Hall Inc Russell/Taylor Oper Mgt 3/e Ch 17 - 30
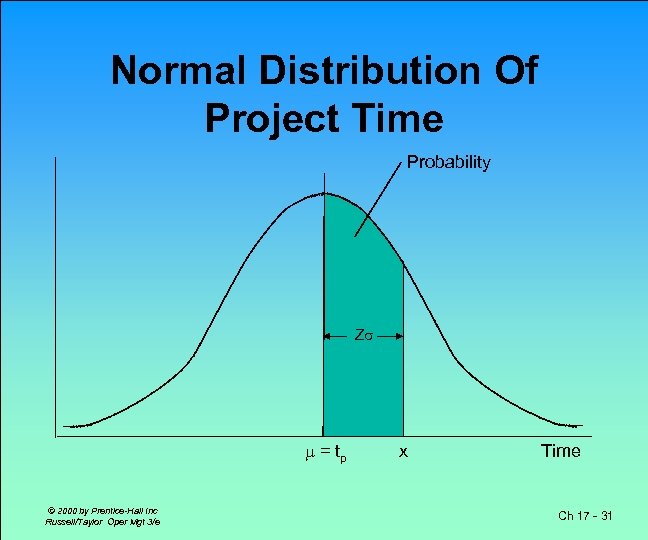
Normal Distribution Of Project Time Probability Z = tp © 2000 by Prentice-Hall Inc Russell/Taylor Oper Mgt 3/e x Time Ch 17 - 31

Probabilistic Analysis Example What is the probability that the project is completed within 30 weeks? © 2000 by Prentice-Hall Inc Russell/Taylor Oper Mgt 3/e Ch 17 - 32
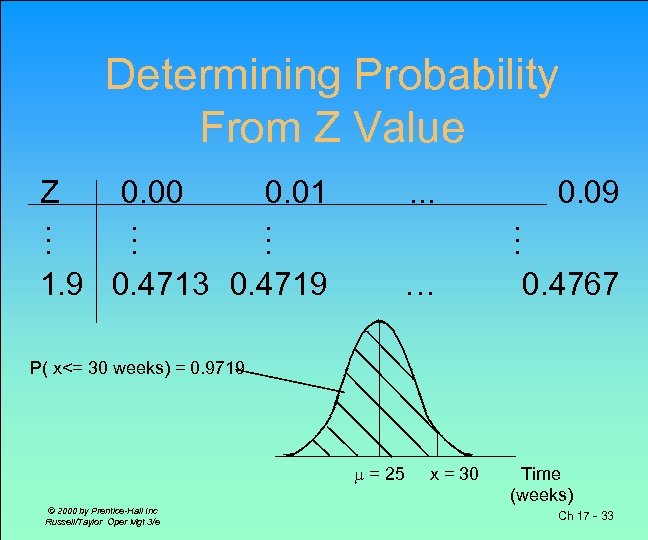
Determining Probability From Z Value Z. . . 0. 00. . . 0. 01. . . 1. 9 0. 4713 0. 4719 … . . . 0. 09 0. 4767 P( x<= 30 weeks) = 0. 9719 = 25 © 2000 by Prentice-Hall Inc Russell/Taylor Oper Mgt 3/e x = 30 Time (weeks) Ch 17 - 33
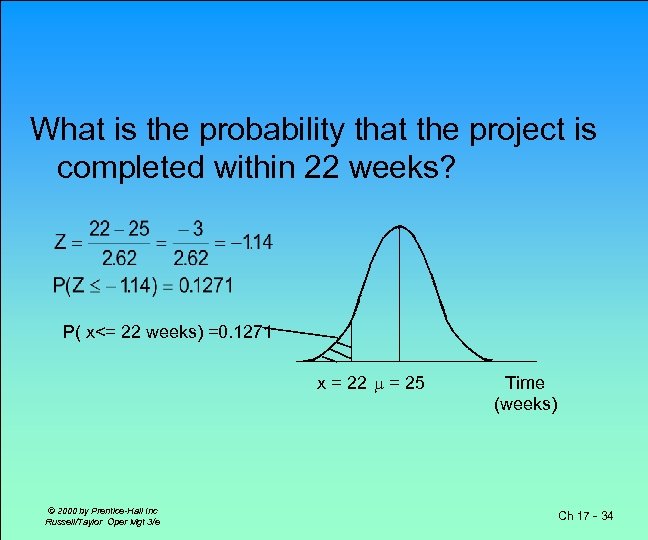
What is the probability that the project is completed within 22 weeks? P( x<= 22 weeks) =0. 1271 x = 22 = 25 © 2000 by Prentice-Hall Inc Russell/Taylor Oper Mgt 3/e Time (weeks) Ch 17 - 34

Project Crashing • Crashing is reducing project time by expending additional resources • Crash time is an amount of time an activity is reduced • Crash cost is the cost of reducing the activity time • Goal is to reduce project duration at minimum cost © 2000 by Prentice-Hall Inc Russell/Taylor Oper Mgt 3/e Ch 17 - 35
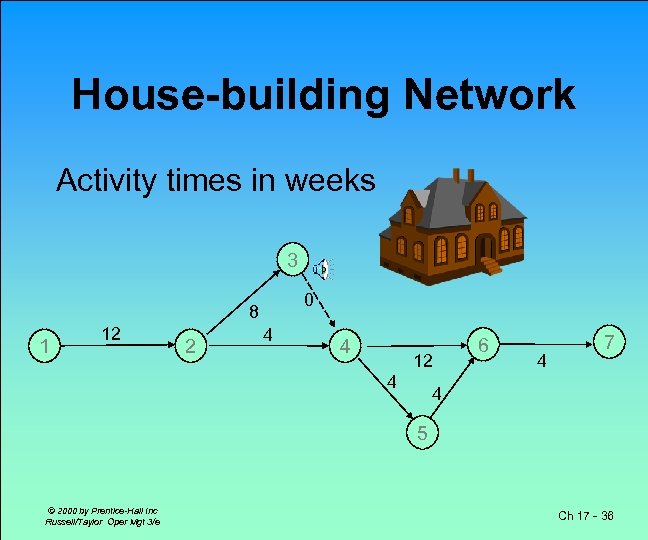
House-building Network Activity times in weeks 3 0 8 1 12 2 4 4 12 4 6 4 7 4 5 © 2000 by Prentice-Hall Inc Russell/Taylor Oper Mgt 3/e Ch 17 - 36
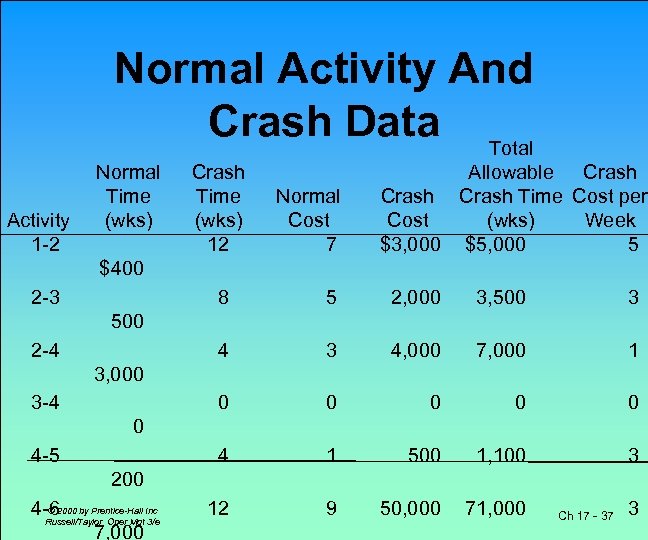
Normal Activity And Crash Data Total Activity 1 -2 Normal Time (wks) Crash Time (wks) 12 Normal Cost 7 Allowable Crash Time Cost per Cost (wks) Week $3, 000 $5, 000 5 $400 2 -3 8 5 2, 000 3, 500 3 4, 000 7, 000 1 0 0 0 4 1 500 1, 100 3 12 9 50, 000 71, 000 500 2 -4 3, 000 3 -4 0 4 -5 200 © 4 -62000 by Prentice-Hall Inc Russell/Taylor Oper Mgt 3/e 7, 000 Ch 17 - 37 3
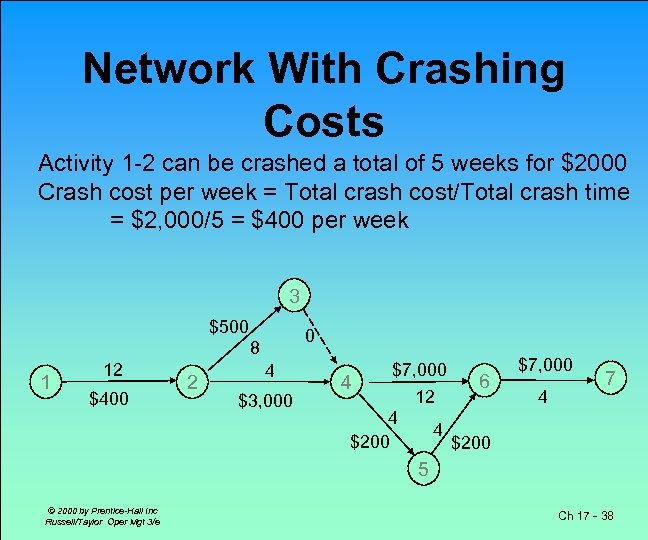
Network With Crashing Costs Activity 1 -2 can be crashed a total of 5 weeks for $2000 Crash cost per week = Total crash cost/Total crash time = $2, 000/5 = $400 per week 3 $500 0 8 1 12 $400 2 4 $3, 000 $7, 000 6 4 12 4 4 $200 $7, 000 4 7 5 © 2000 by Prentice-Hall Inc Russell/Taylor Oper Mgt 3/e Ch 17 - 38
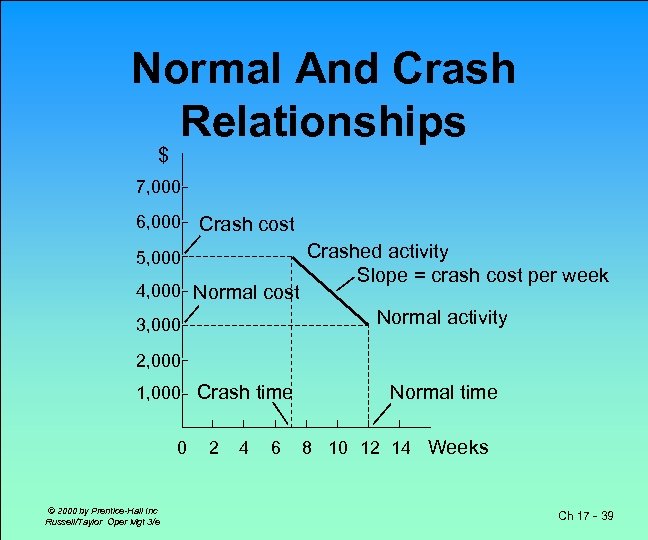
Normal And Crash Relationships $ 7, 000 6, 000 Crash cost 5, 000 4, 000 Normal cost Crashed activity Slope = crash cost per week Normal activity 3, 000 2, 000 1, 000 Crash time 0 © 2000 by Prentice-Hall Inc Russell/Taylor Oper Mgt 3/e 2 4 6 Normal time 8 10 12 14 Weeks Ch 17 - 39

Crashing Solution Activity Normal Time (wks) 1 -2 Crash Time (wks) Crash Time Used Crash Cost per Week Crashing Cost Incurred 12 7 5 $400 8 4 0 4 12 5 3 0 1 9 3 0 0 0 3 500 3, 000 0 200 7, 000 4 4 1 3 12 0 1 $2, 000 2 -3 2 -4 3 -4 4 -5 4 -6 1, 50 21, 000 5 -6 6 -7 © 2000 by Prentice-Hall Inc Russell/Taylor Oper Mgt 3/e 200 7, 00 $31, 500 - 40 Ch 17
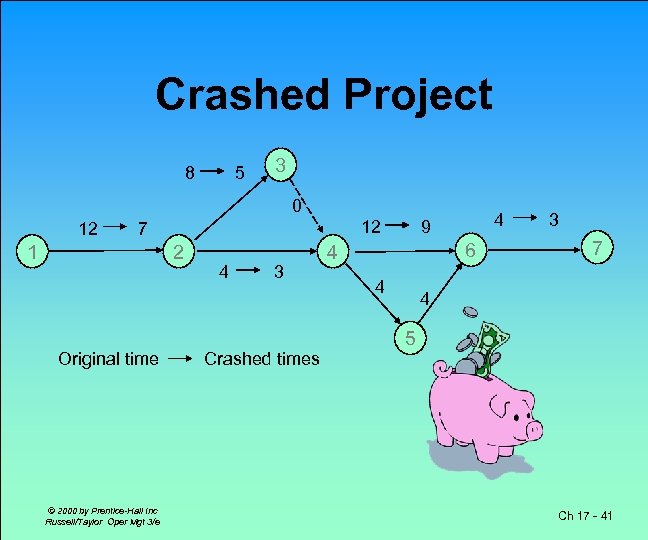
Crashed Project 8 5 3 0 12 12 7 1 2 Original time © 2000 by Prentice-Hall Inc Russell/Taylor Oper Mgt 3/e 4 3 Crashed times 4 9 6 4 4 3 7 4 5 Ch 17 - 41

Time-Cost Relationship • Crashing costs increase as project duration decreases • Indirect costs increase as project duration increases • Reduce project length as long as crashing costs are less than indirect costs © 2000 by Prentice-Hall Inc Russell/Taylor Oper Mgt 3/e Ch 17 - 42
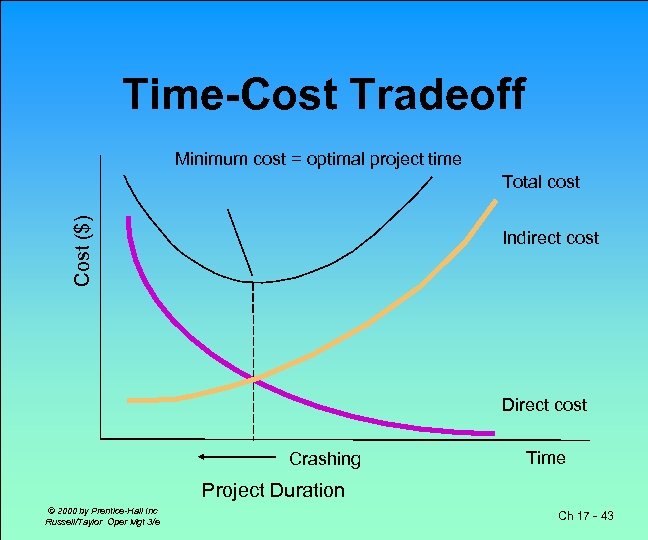
Time-Cost Tradeoff Minimum cost = optimal project time Cost ($) Total cost Indirect cost Direct cost Crashing Time Project Duration © 2000 by Prentice-Hall Inc Russell/Taylor Oper Mgt 3/e Ch 17 - 43
efd9ff5203f3f032d089a68f4475cc2d.ppt