8a1615ee1a32b83e9b68cf17e0dd7845.ppt
- Количество слайдов: 23

Probabilistic Reasoning • Bayesian Belief Networks • Constructing Bayesian Networks • Representing Conditional Distributions • Summary

Bayesian Belief Networks (BBN) A Bayesian Belief Network is a method to describe the joint probability distribution of a set of variables. Let x 1, x 2, …, xn be a set of random variables. A Bayesian Belief Network or BBN will tell us the probability of any combination of x 1, x 2 , . . , xn.

Representation A BBN represents the joint probability distribution of a set of variables by explicitly indicating the assumptions of conditional independence through the following: a) b) c) d) Nodes representing random variables Directed links representing relations. Conditional probability distributions. The graph is a directed acyclic graph.
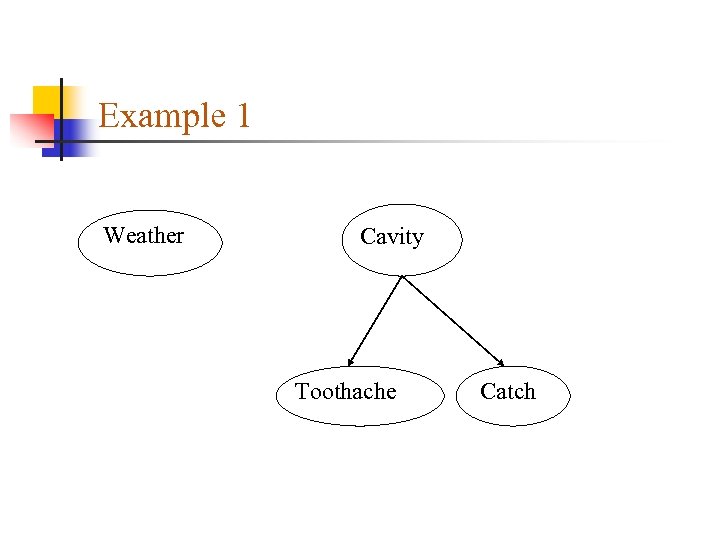
Example 1 Weather Cavity Toothache Catch
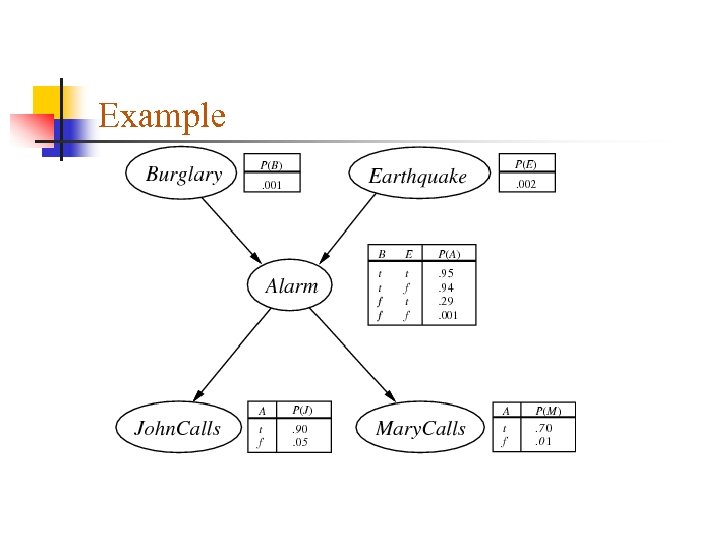
Example

Representation Each variable is independent of its non-descendants given its predecessors. We say x 1 is a descendant of x 2 if there is a direct path from x 2 to x 1. Example: Predecessors of Alarm: Burglary, Earthquake.

Joint Probability Distribution To compute the joint probability distribution of a set of variables given a Bayesian Belief Network we simply use the following formula: P(x 1, x 2, …, xn) = Π P(xi | Parents(xi)) Where parents are the immediate predecessors of xi.

Joint Probability Distribution Example: P(John, Mary, Alarm, ~Burglary, ~Earthquake) : P(John|Alarm) P(Mary|Alarm) P(Alarm|~Burglary ^ ~Earthquake) P(~Burglary) P(~Earthquake) = 0. 00062
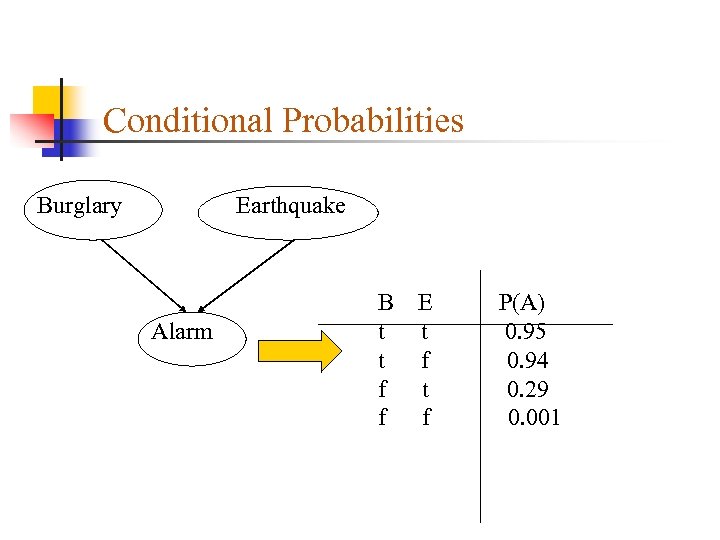
Conditional Probabilities Burglary Earthquake Alarm B t t f f E t f P(A) 0. 95 0. 94 0. 29 0. 001

Probabilistic Reasoning • Bayesian Belief Networks • Constructing Bayesian Networks • Representing Conditional Distributions • Summary

Constructing Bayesian Networks Choose the right order from causes to effects. P(x 1, x 2, …, xn) = P(xn|xn-1, . . , x 1)P(xn-1, …, x 1) = Π P(xi|xi-1, …, x 1) -- chain rule Example: P(x 1, x 2, x 3) = P(x 1|x 2, x 3)P(x 2|x 3)P(x 3)
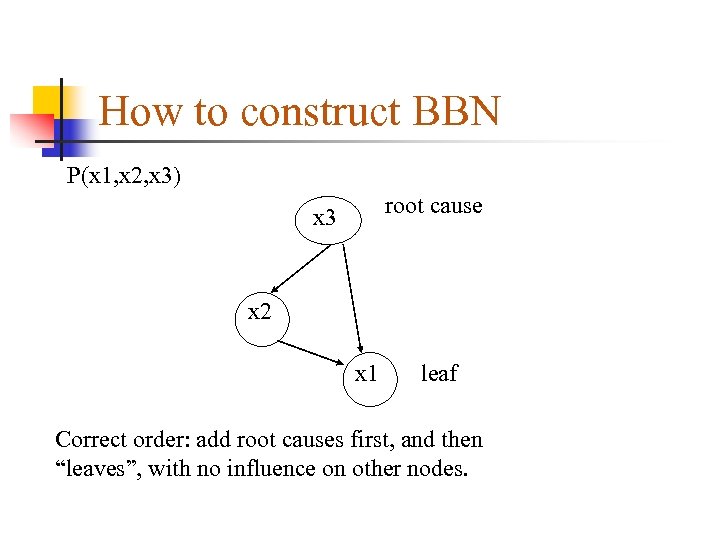
How to construct BBN P(x 1, x 2, x 3) root cause x 3 x 2 x 1 leaf Correct order: add root causes first, and then “leaves”, with no influence on other nodes.

Compactness BBN are locally structured systems. They represent joint distributions compactly. Assume n random variables, each influenced by k nodes. Size BBN: n 2 k Full size: 2 n

Probabilistic Reasoning • Bayesian Belief Networks • Constructing Bayesian Networks • Representing Conditional Distributions • Summary
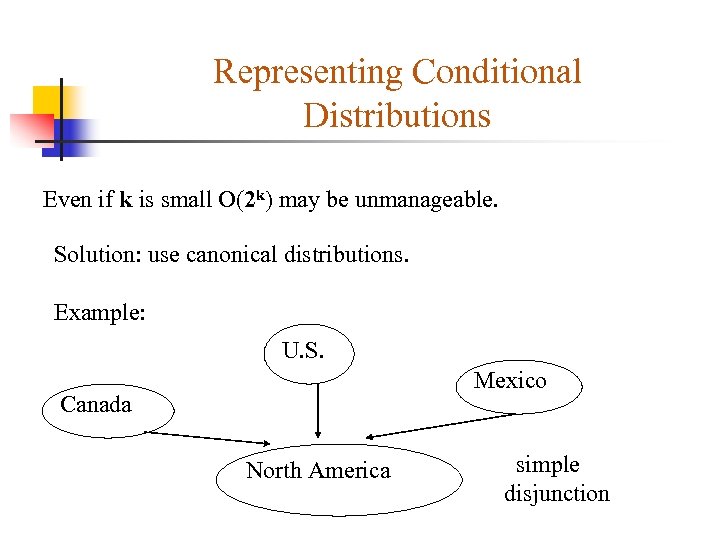
Representing Conditional Distributions Even if k is small O(2 k) may be unmanageable. Solution: use canonical distributions. Example: U. S. Mexico Canada North America simple disjunction
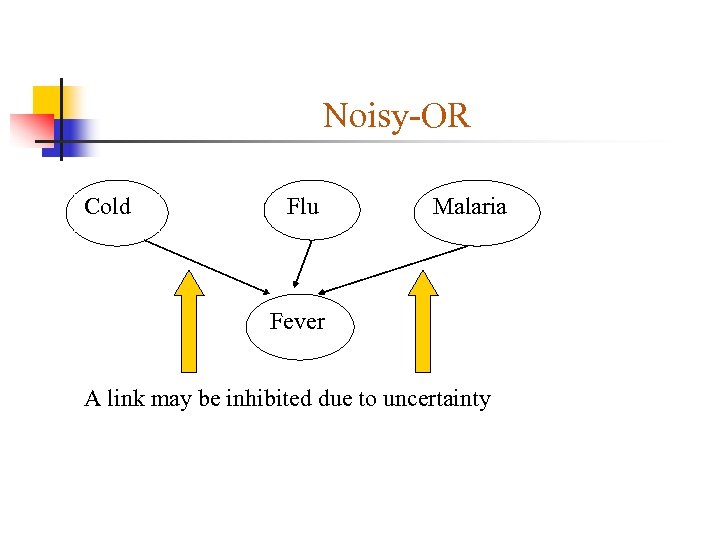
Noisy-OR Cold Flu Malaria Fever A link may be inhibited due to uncertainty

Noisy-OR Inhibitions probabilities: P(~fever | cold, ~flu, ~malaria) = 0. 6 P(~fever | ~cold, flu, ~malaria) = 0. 2 P(~fever | ~cold, ~flu, malaria) = 0. 1

Noisy-OR Now the whole probability can be built: P(~fever | cold, ~flu, malaria) = 0. 6 x 0. 1 P(~fever | cold, flu, ~malaria) = 0. 6 x 0. 2 P(~fever | ~cold, flu, malaria) = 0. 2 x 0. 1 P(~fever | cold, flu, malaria) = 0. 6 x 0. 2 x 0. 1 P(~fever | ~cold, ~flu, ~malaria) = 1. 0

Continuous Variables Continuous variables can be discretized. Or define probability density functions Example: Gaussian distribution. A network with both variables is called a Hybrid Bayesian Network.
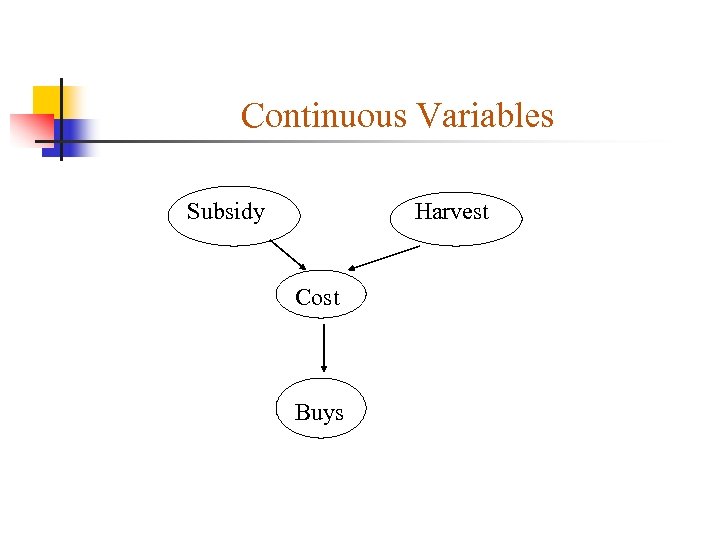
Continuous Variables Subsidy Harvest Cost Buys
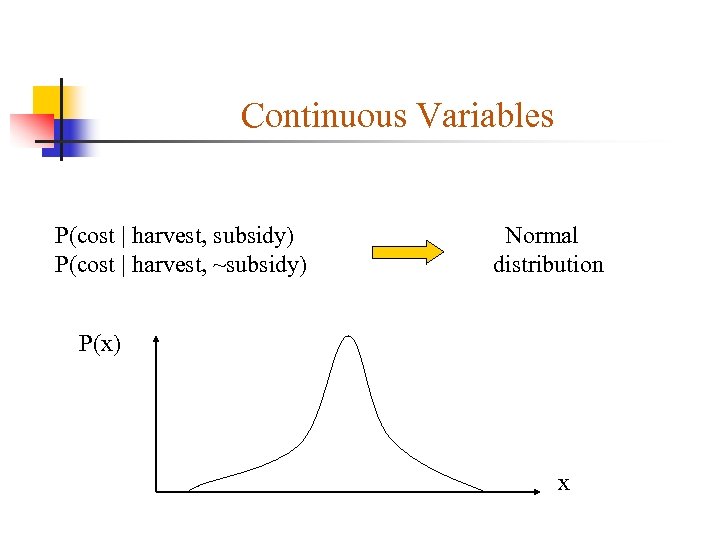
Continuous Variables P(cost | harvest, subsidy) P(cost | harvest, ~subsidy) Normal distribution P(x) x

Probabilistic Reasoning • Bayesian Belief Networks • Constructing Bayesian Networks • Representing Conditional Distributions • Summary

Summary • Bayesian networks are directed acyclic graphs that concisely represent conditional independence relations among random variables. • BBN specify the full joint probability distribution of a set of variables. • BBN can by hybrid, combining categorical variables with numeric variables.
8a1615ee1a32b83e9b68cf17e0dd7845.ppt