3e172c23a5459261cd8c5c1dd91c87dd.ppt
- Количество слайдов: 25

Proactive-reactive project scheduling with flexibility and quality requirements Mario Brčić Prof. dr. sc. Damir Kalpić University of Zagreb, Faculty of Electrical Engineering and Computing August 2014

Overview • Introduction • Project scheduling under uncertainty • Previous research results • New model • Preliminary results • Conclusion 2
Introduction Increased services and products complexity More complex projects • High activity count • Subcontractors • Suppliers • Due dates Coordination 3
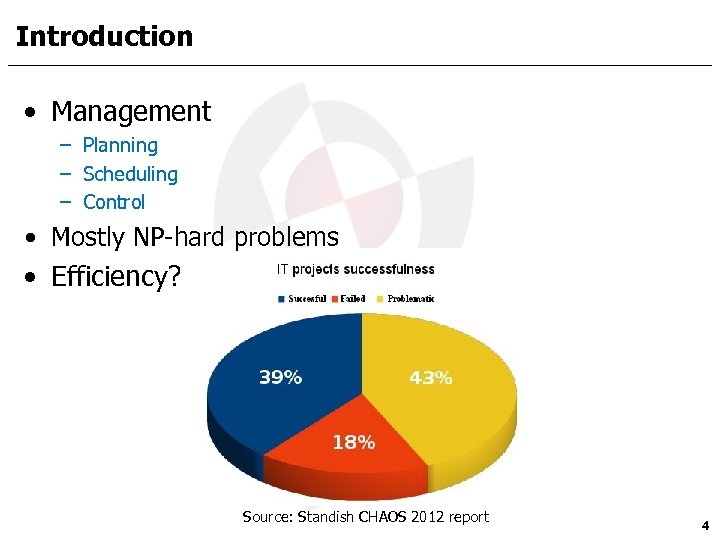
Introduction • Management – Planning – Scheduling – Control • Mostly NP-hard problems • Efficiency? Source: Standish CHAOS 2012 report 4

Introduction • Efficiency? – Boeing 787 Dreamliner • Large degree of outsourcing • Exceeding budget by ~150 % (>10 bn $) • Exceeding planned due dates by >60% (>3 years) • Billions of dollars of additional losses due to cancelled orders, delivery delay penalties and damage to the reputation – Lockheed Martin F-35 • Exceeing budget by >60% (>150 bn $) • Exceeding planned due dates by >60% (~7 years) • Still in execution 5

Introduction Historical sequence • Critical Path Method • Program evaluation and review technique (PERT) • Resource Constrained Project Scheduling Problems (RCPSP) • Critical Chain Project Management • RCPSP generalizations taking into account the uncertainty 6

Project Scheduling under Uncertainty • Stochastic Resource Constrained Project Scheduling Problems (SRCPSP) – probability distribution for uncertainty is known (described by events) – random variables model uncertain elements • Fuzzy Resource Constrained Project Scheduling Problems – degrees of fuzzy set memberships is known for uncertainty – fuzzy numbers model uncertain elements • Robust Resource Constrained Project Scheduling Problems – only possible outcomes of uncertain events are known – minimax, minimin, minimax regret, . . 7

Project Scheduling under Uncertainty • Baseline schedule – Coordination • Commiting between project collaborators – Prior to the project execution start 8

Project Scheduling under Uncertainty • Solutions: policies (strategies) – Functions that map from the states to the controls – Candidate solution evaluation often “too expensive” - simulation • Solution approaches – Predictive • Point estimates, no anticipation of variability – Proactive • Increasing the degree of robustness – Reactive • Dynamic changes • Baseline repairing • Completely online (dynamic) methods Static 9

RCPSP • Combinatorial problem defined by n-tuple (V, E, d, R, B, D, f) • Activities - V={0, . . , n+1} V’=V/{0, n+1} • Precedence relations – Directed acyclic graph G(A, E) • Activity durations • Renewable resources - R={R 1, . . . , Rr} • Resource availabilities • Activity demands • Objective/cost function - c: X→R Single execution mode 10

RCPSP with uncertain activity durations • Combinatorial problem defined by n-tuple (V, E, Ω, F, P, d, R, B, D, f) • Activities - V={0, . . , n+1} V’=V/{0, n+1} • Precedence relations – Directed acyclic graph G(A, E) Random variable • Activity durations • Renewable resources - R={R 1, . . . , Rr} • Resource availabilities • Activity demands • Objective/cost function - c: S×Π→R • Probability space - (Ω, F, P) More complex domain Information about uncertainty 11

Previous research results • Reactive procedures • Möhring et al. 1984 – Theoretical basis – Policy families • Parameterized policies • Choi 2007, Csaji 2008 – Markov decision process – Reinforcement learning • Offline computational burden 12

Previous research results • Proactive procedures – Protected baseline • Robustness measures – Quality robustness • Timely project completion probability • Expected due date exceeding cost – Schedule stability measure - Leus Herroelen, 2004 – Combined robustness measures • Bi-criteria measure of stability and quality 13

Previous research results • Proactive-reactive procedures – Combined measures : stability+quality • Van de Vonder et al. , 2006 – Defined new reactive policy family – Offline policy calculation • Van de Vonder et al. , 2007 – – Baseline schedule repair policies Sampling with point estimates Don’t change baseline schedule Online policy calculation 14

Previous research results • Deblaere et al. , 2011 – Combined robustness measure • Expected due date penalty/bonus • Expected asymmetric schedule stability cost – Resource-based policies with release times • Priority vector • Release times vector – Simulation-based descend (SBD) – Offline computational burden – Integrated procedure for finding proactive schedule and reactive policy – The best performance so far 15

Previous research results • Baseline schedule fixed – Excessive commiting problem • Lambrechts, 2007 – Proactive rescheduling • Bi-criteria objective function – New schedule with increased proactivity – New schedule “close” to the preceding • Taboo search for uncertain resource availabilities • Moderate results! – Immediate instability costs outweigh the potential gains 16

Goal • Proactive rescheduling – Schedule stability measure “useless” • Unit cost identical for all changes over each activity – Changes over baseline not desirable – Implies long-term commiting – New robustness measures • Demeulemeester and Herroelen, 2011 17

New robustness measure • Robustness measure (CBF) which depends on: – Size of the schedule change – Temporal distance of the change from the present |x-y| t time min(x, y)-t – More distant changes are more likely to cost less 18
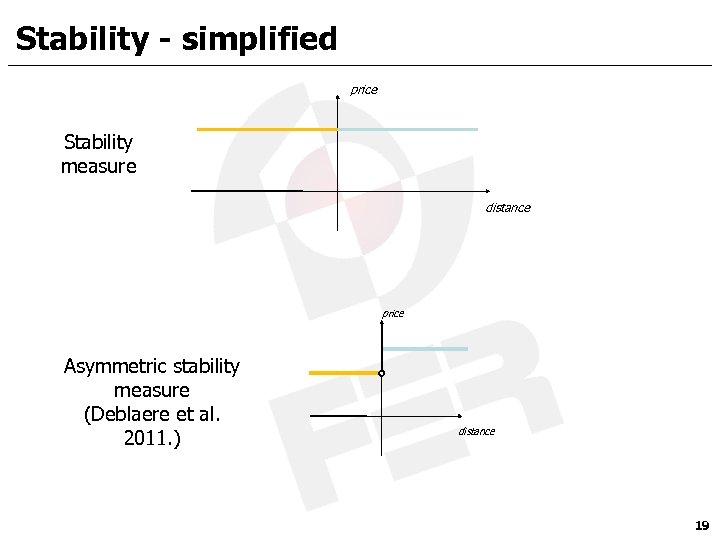
Stability - simplified price Stability measure distance price Asymmetric stability measure (Deblaere et al. 2011. ) distance 19

Computational study • Setting similar to Deblare et al. , 2011 (smaller scale) 50*6 PSPLIB 30 -activity projects + 50*6 PSPLIB 60 -activity projects • 1000 scenarios per project • Benchmark – Deblaere et al. , 2011. – Mean cost and variance 20

Preliminary performance • 30 -activity projects – Improvement in both performance and variance –. . . but greater computation time • 60 -activity projects – Even greater improvement in both performance and variance –. . . again paying with even greater computation time 21

Conclusion • Complex projects – Multiple collaborators - coordination – Due dates • Stability measure – Excessive commitment – Fixed baseline • Proactive rescheduling – Cost-based flexibility – Simulation-based algorithm – Improvement over the best available alternative 22

Questions 23
![Literature [1] The Standish Group International, “CHAOS Summary 2009, ” 2009. [2] D. Gates, Literature [1] The Standish Group International, “CHAOS Summary 2009, ” 2009. [2] D. Gates,](https://present5.com/presentation/3e172c23a5459261cd8c5c1dd91c87dd/image-24.jpg)
Literature [1] The Standish Group International, “CHAOS Summary 2009, ” 2009. [2] D. Gates, “Boeing celebrates 787 delivery as program’s costs top $32 billion, ” The Seattle Times. [Online]. Available: http: //seattletimes. com/html/businesstechnology/2016310102_boeing 25. html. [Accessed: 10 Mar-2014]. [3] P. Giblin, “F-35 behind schedule, over budget, ” azcentral. com. [Online]. Available: http: //www. azcentral. com/news/arizona/articles/20140208 fighter-plane-behind-schedule-over-budget. html. [Accessed: 10 -Mar-2014]. [4] E. Demeulemeester and W. Herroelen, Robust Project Scheduling. Now Publishers Inc, 2011. [5] R. H. Möhring, F. J. Radermacher, and G. Weiss, “Stochastic scheduling problems I — General strategies, ” Z. Für Oper. Res. , vol. 28, no. 7, pp. 193– 260, Nov. 1984. [6] R. H. Möhring and F. J. Radermacher, “Introduction to Stochastic Scheduling Problems, ” in Contributions to Operations Research, P. D. K. Neumann and P. D. D. Pallaschke, Eds. Springer Berlin Heidelberg, 1985, pp. 72– 130. [7] F. Stork, “Stochastic resource-constrained project scheduling, ” Ph. D Thesis, Technical University at Berlin, Germany, 2001. [8] F. Ballestín and R. Leus, “Resource‐Constrained Project Scheduling for Timely Project Completion with Stochastic Activity Durations, ” Prod. Oper. Manag. , vol. 18, no. 4, pp. 459– 474, Jul. 2009. [9] B. Ashtiani, R. Leus, and M. -B. Aryanezhad, “New competitive results for the stochastic resourceconstrained project scheduling problem: exploring the benefits of pre-processing, ” J Sched. , vol. 14, no. 2, pp. 157– 171, Apr. 2011. [10] B. C. Csáji and L. Monostori, “Adaptive stochastic resource control: a machine learning approach, ” J. Artif. Intell. Res. , vol. 32, no. 1, pp. 453– 486, 2008. 24
![Literature [11] J. Choi, M. J. Realff, and J. H. Lee, “A Q-Learning-based method Literature [11] J. Choi, M. J. Realff, and J. H. Lee, “A Q-Learning-based method](https://present5.com/presentation/3e172c23a5459261cd8c5c1dd91c87dd/image-25.jpg)
Literature [11] J. Choi, M. J. Realff, and J. H. Lee, “A Q-Learning-based method applied to stochastic resource constrained project scheduling with new project arrivals, ” Int. J. Robust Nonlinear Control, vol. 17, no. 13, pp. 1214– 1231, Sep. 2007. [12] C. Artigues, R. Leus, and F. Talla Nobibon, “Robust optimization for resource-constrained project scheduling with uncertain activity durations, ” Flex. Serv. Manuf. J. , vol. to appear, pp. 1– 31, 2012. [13] R. Leus and W. Herroelen, “Stability and resource allocation in project planning, ” IIE Trans. , vol. 36, no. 7, pp. 667– 682, 2004. [14] F. Deblaere, E. Demeulemeester, W. Herroelen, and S. Van de Vonder, “Robust Resource Allocation Decisions in Resource‐Constrained Projects, ” Decis. Sci. , vol. 38, no. 1, pp. 5– 37, Feb. 2007. [15] S. Van de Vonder, E. Demeulemeester, R. Leus, and W. Herroelen, “Proactive-Reactive Project Scheduling Trade-Offs and Procedures, ” in Perspectives in Modern Project Scheduling, vol. 92, J. Józefowska and J. Weglarz, Eds. Springer US, 2006, pp. 25– 51. [16] S. Van de Vonder, F. Ballestin, E. Demeulemeester, and W. Herroelen, “Heuristic procedures for reactive project scheduling, ” Comput. Ind. Eng. , vol. 52, no. 1, pp. 11– 28, 2007. [17] F. Deblaere, E. Demeulemeester, and W. Herroelen, “Proactive policies for the stochastic resourceconstrained project scheduling problem, ” Eur. J. Oper. Res. , vol. 214, no. 2, pp. 308– 316, Oct. 2011. [18] O. Lambrechts, “Robust project scheduling subject to resource breakdowns, ” Ph. D Thesis, Faculty of Business and Economics, Katholieke Universiteit Leuven, Belgium, 2007. [19] M. Brcic, D. Kalpic and M. Katic, “Proactive Reactive Scheduling in Resource Constrained Projects with Flexibility and Quality Robustness Requirements” in Lecture Notes in Computer Science vol. 8596, 2014. , pp. 112 -124 25
3e172c23a5459261cd8c5c1dd91c87dd.ppt