Призма Определение призмы Виды призм Определение Призмой

Призма

Определение призмы. Виды призм. Определение. Призмой называется многоугольник, две грани которого, называемые основаниями призмы, равные многоугольники с соответственно параллельными сторонами, а остальные грани – параллелограммы, у каждого из которых две стороны являются соответственными сторонами оснований.

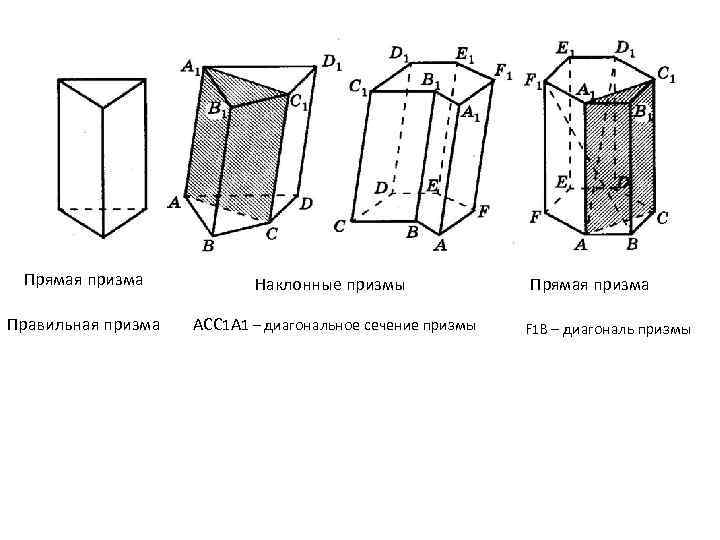Прямая призма Наклонные призмы Правильная призма ACC 1 A 1 – диагональное сечение призмы Прямая призма F 1 B – диагональ призмы

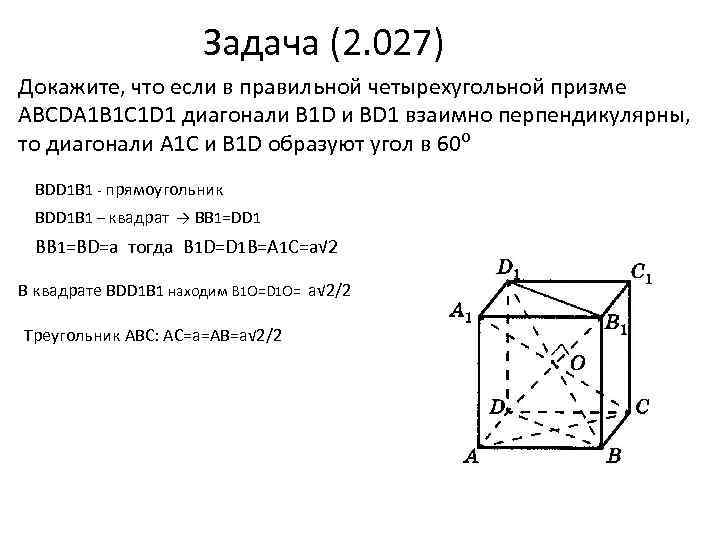Задача (2. 027) Докажите, что если в правильной четырехугольной призме АВCDA 1 B 1 C 1 D 1 диагонали B 1 D и BD 1 взаимно перпендикулярны, то диагонали A 1 C и B 1 D образуют угол в 60⁰ BDD 1 B 1 - прямоугольник BDD 1 B 1 – квадрат → BB 1=DD 1 BB 1=BD=a тогда B 1 D=D 1 B=A 1 C=a√ 2 В квадрате BDD 1 B 1 находим B 1 O=D 1 O= a√ 2/2 Треугольник ABC: AC=a=AB=a√ 2/2

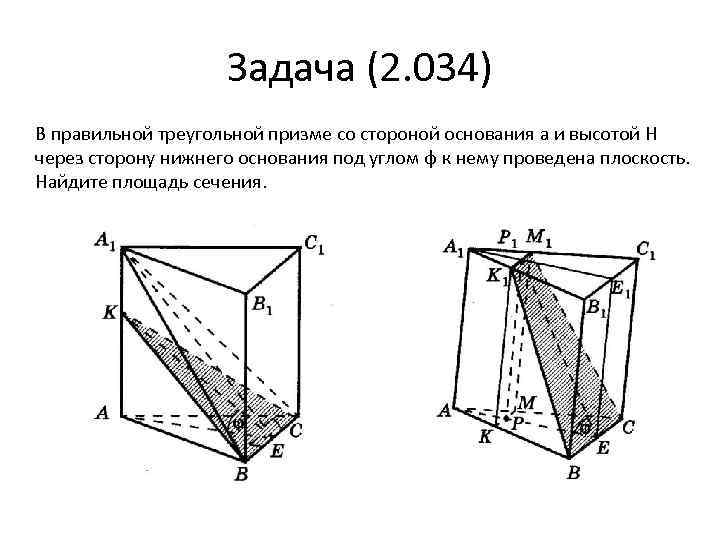Задача (2. 034) В правильной треугольной призме со стороной основания a и высотой H через сторону нижнего основания под углом φ к нему проведена плоскость. Найдите площадь сечения.

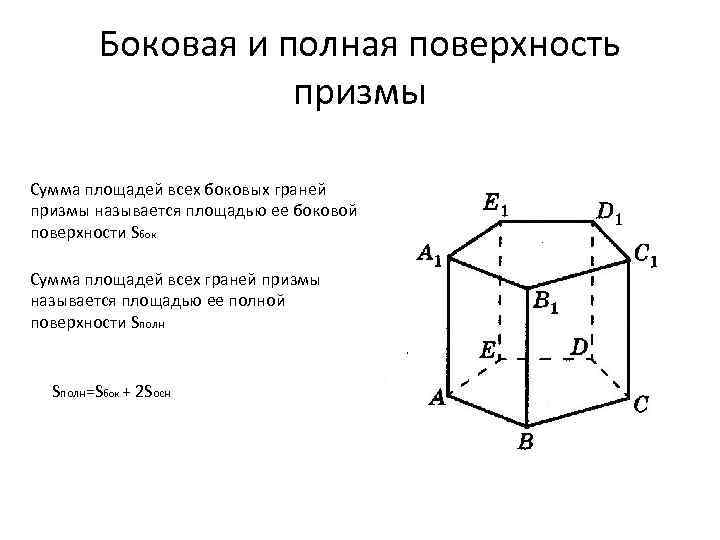Боковая и полная поверхность призмы Сумма площадей всех боковых граней призмы называется площадью ее боковой поверхности Sбок Сумма площадей всех граней призмы называется площадью ее полной поверхности Sполн=Sбок + 2 Sосн

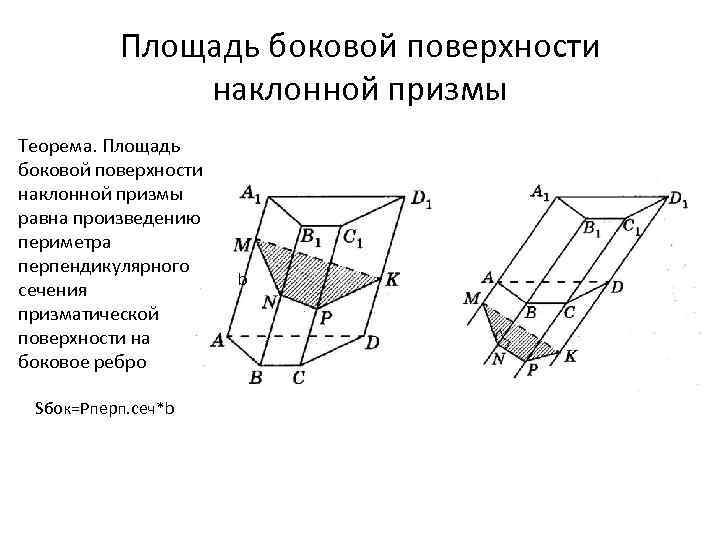Площадь боковой поверхности наклонной призмы Теорема. Площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения призматической поверхности на боковое ребро Sбок=Pперп. сеч*b b

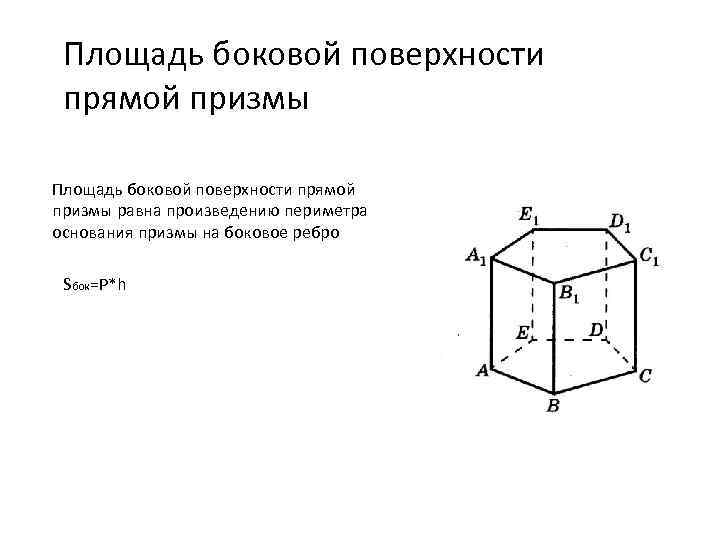Площадь боковой поверхности прямой призмы равна произведению периметра основания призмы на боковое ребро Sбок=P*h

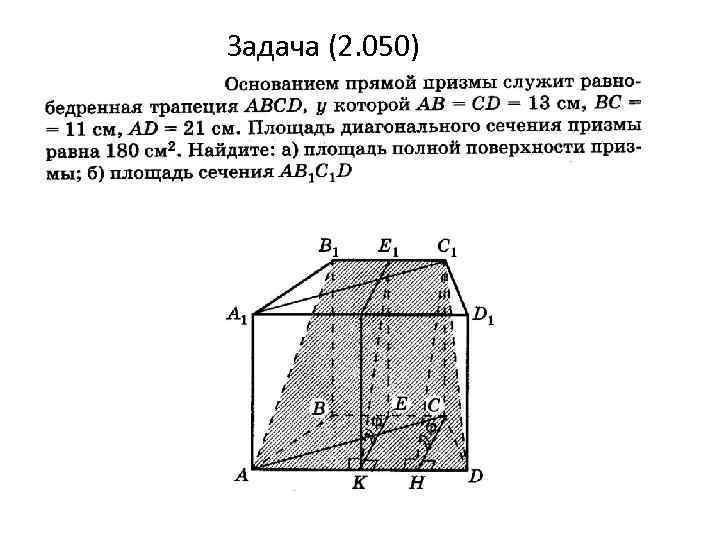Задача (2. 050)

Объем • Объем призмы равен произведению основания на высоту • V=Sосн*h