Призма Геометрия является самым могущественным средством для изощрения

Призма Геометрия является самым могущественным средством для изощрения наших умственных способностей и дает нам возможность правильно мыслить и рассуждать. Г. Галилей

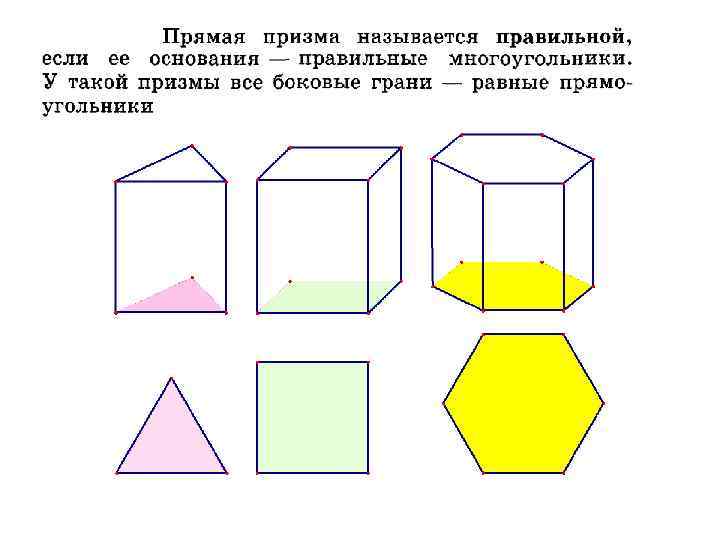
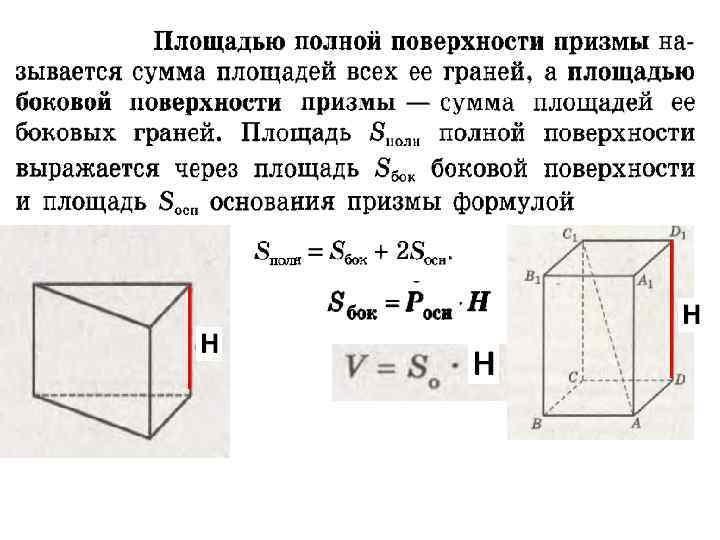
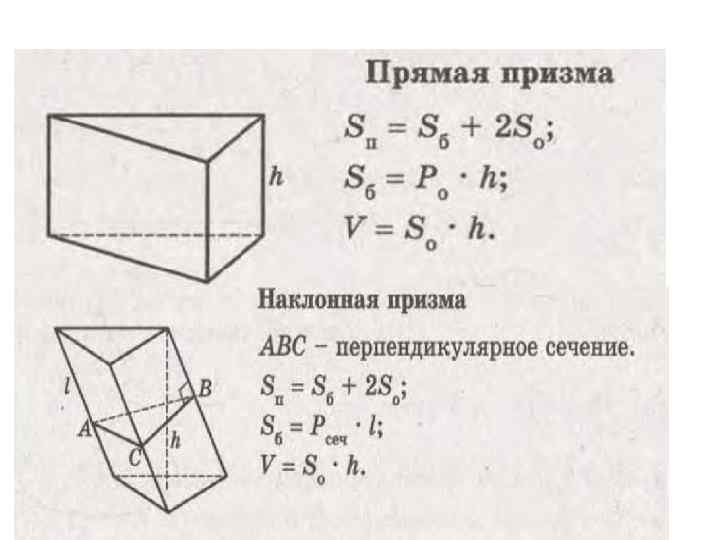
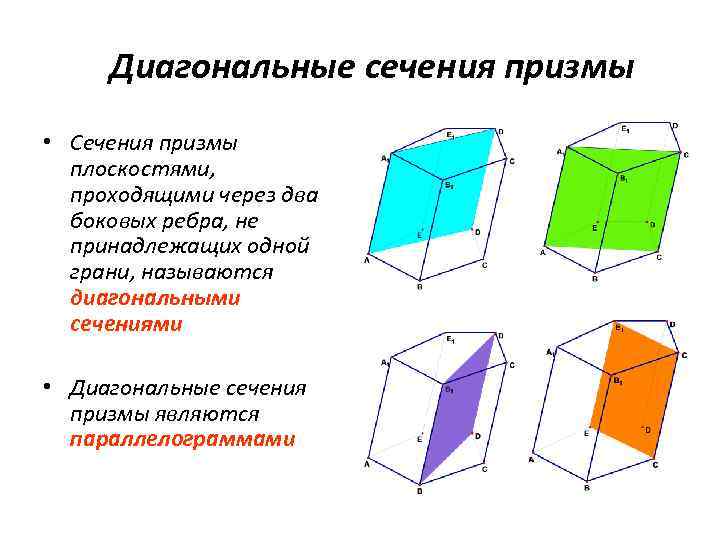Диагональные сечения призмы • Сечения призмы плоскостями, проходящими через два боковых ребра, не принадлежащих одной грани, называются диагональными сечениями • Диагональные сечения призмы являются параллелограммами

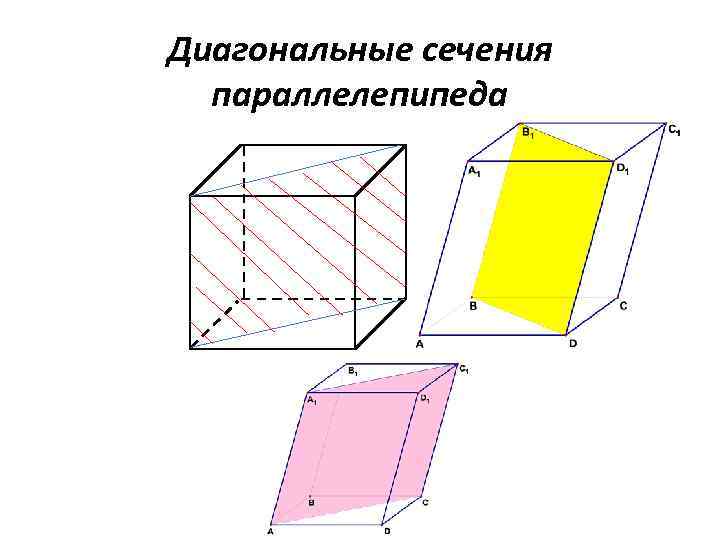Диагональные сечения параллелепипеда

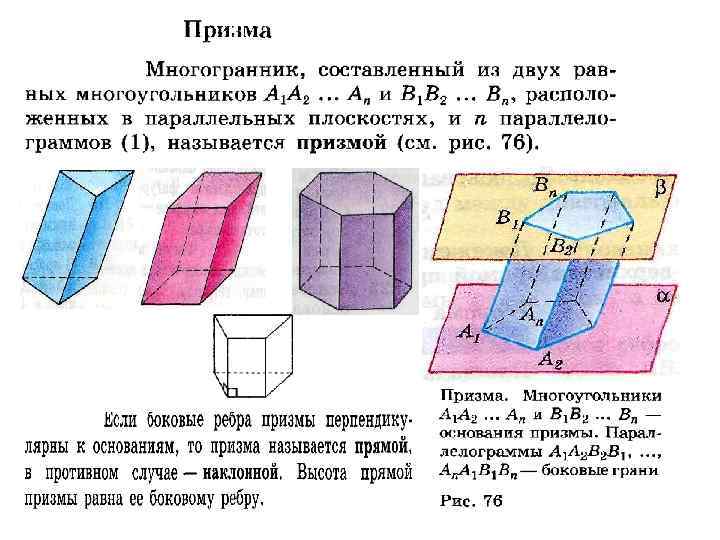
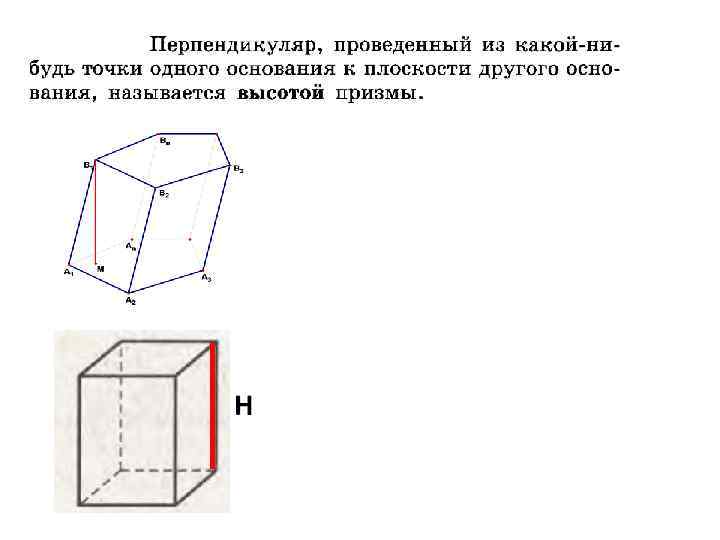
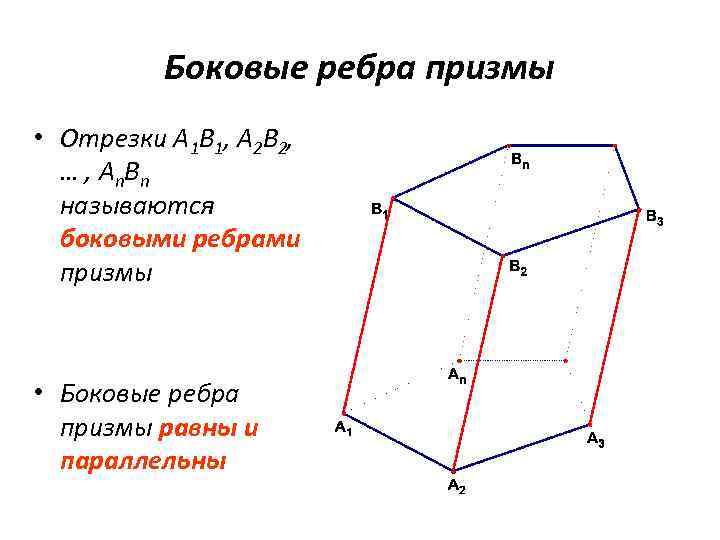Боковые ребра призмы • Отрезки A 1 B 1, A 2 B 2, … , A n. B n называются боковыми ребрами призмы • Боковые ребра призмы равны и параллельны

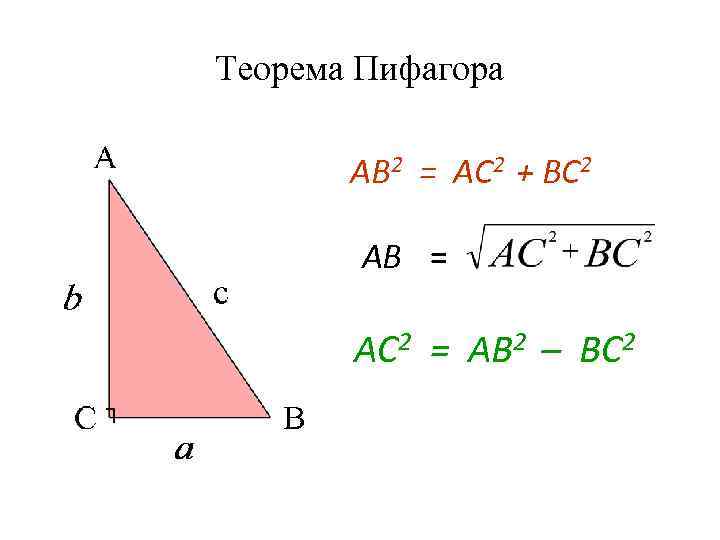Теорема Пифагора АВ 2 = АС 2 + ВС 2 АВ = АС 2 = АВ 2 – ВС 2 ┐

Р=4 а Р=2(а+в) Р=4 а Р=3 а

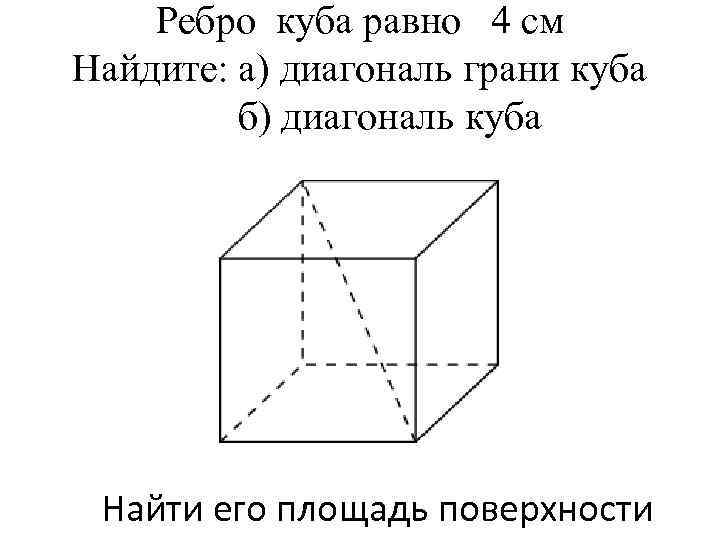Ребро куба равно 4 см Найдите: а) диагональ грани куба б) диагональ куба Найти его площадь поверхности

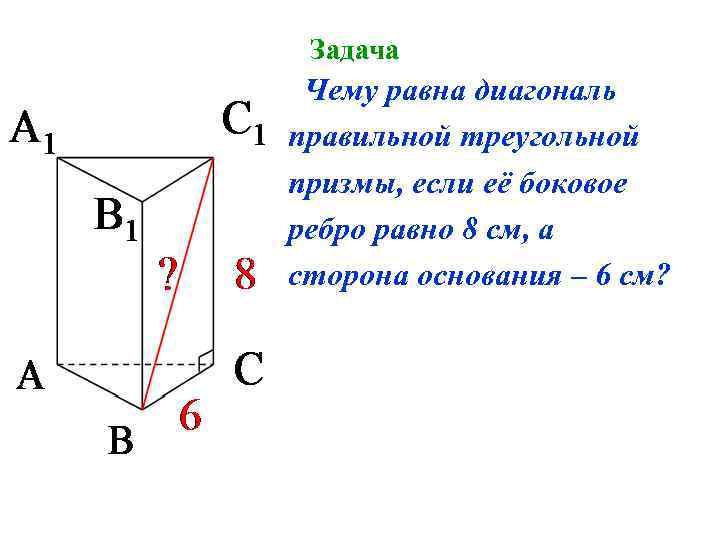Задача Чему равна диагональ правильной треугольной призмы, если её боковое ребро равно 8 см, а сторона основания – 6 см?

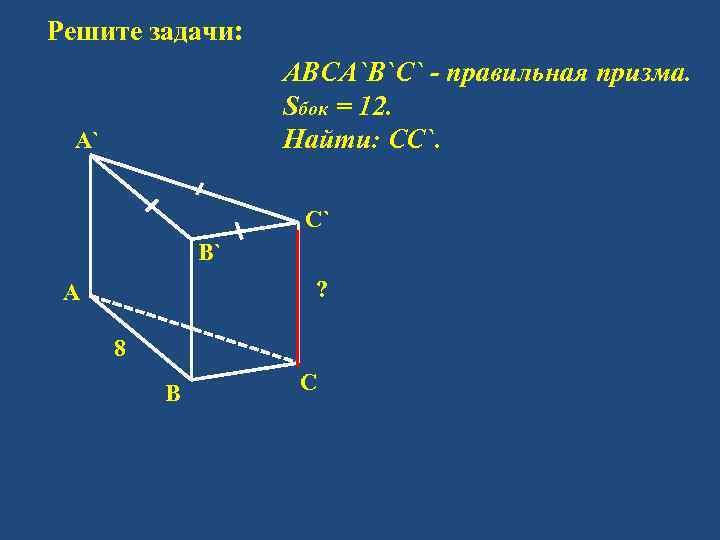Решите задачи: АВСА`B`С` - правильная призма. Sбок = 12. Найти: CC`. А` C` B` ? А 8 B C

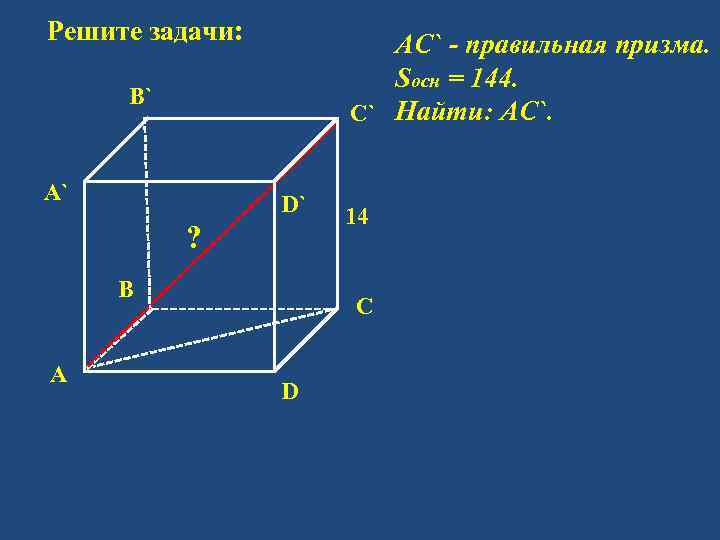Решите задачи: АС` - правильная призма. Sосн = 144. C` Найти: AC`. B` А` D` ? B А 14 C D

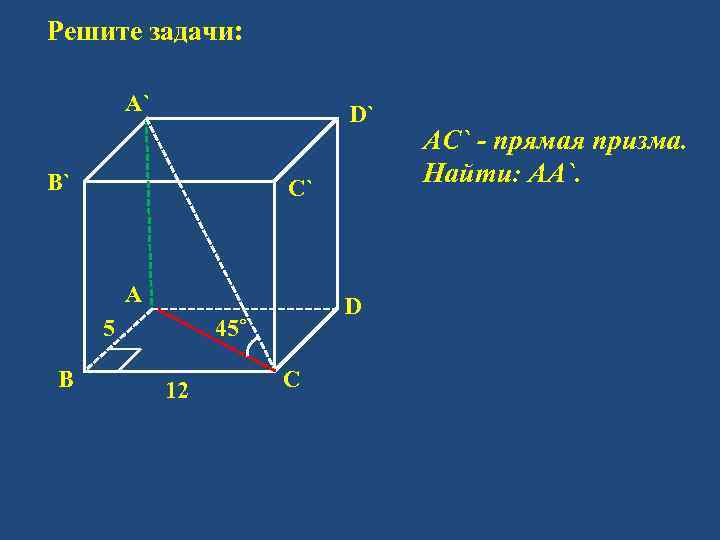Решите задачи: А` D` B` C` А 5 B D 45˚ 12 C АС` - прямая призма. Найти: АА`.

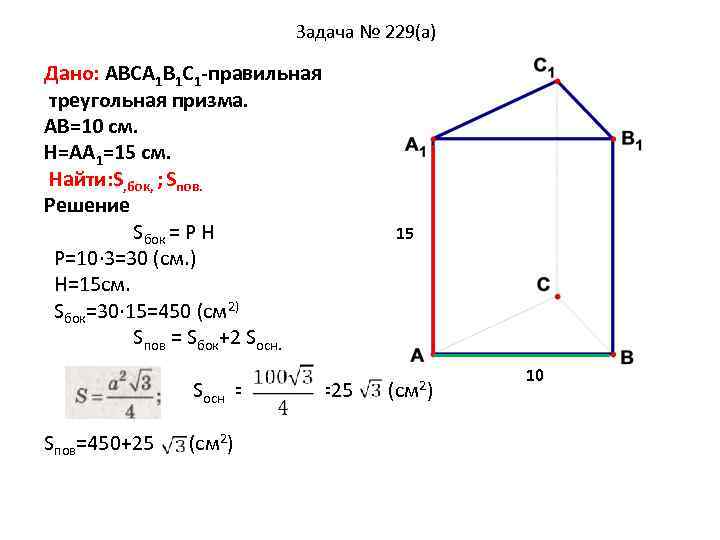Задача № 229(а) Дано: АВСА 1 В 1 С 1 -правильная треугольная призма. АВ=10 см. H=АА 1=15 см. Найти: S, бок, ; Sпов. Решение Sбок = Р H Р=10∙ 3=30 (см. ) H=15 см. Sбок=30∙ 15=450 (см 2) Sпов = Sбок+2 Sосн. . Sпов=450+25 Sосн = (см 2) =25 15 (см 2) 10

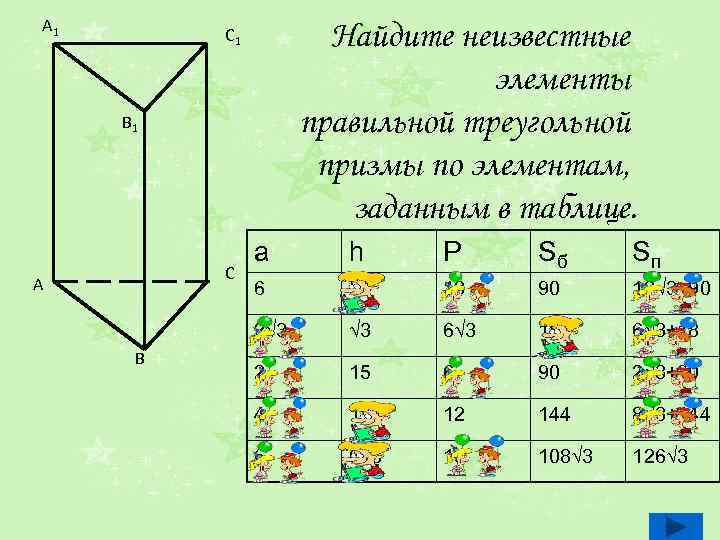A 1 Найдите неизвестные элементы правильной треугольной призмы по элементам, заданным в таблице. C 1 B h P Sб Sп 6 5 18 90 18√ 3+90 2√ 3 C A a √ 3 6√ 3 18 6√ 3+18 2 15 6 90 2√ 3+90 4 12 12 144 8√ 3+144 6 6√ 3 18 108√ 3 126√ 3

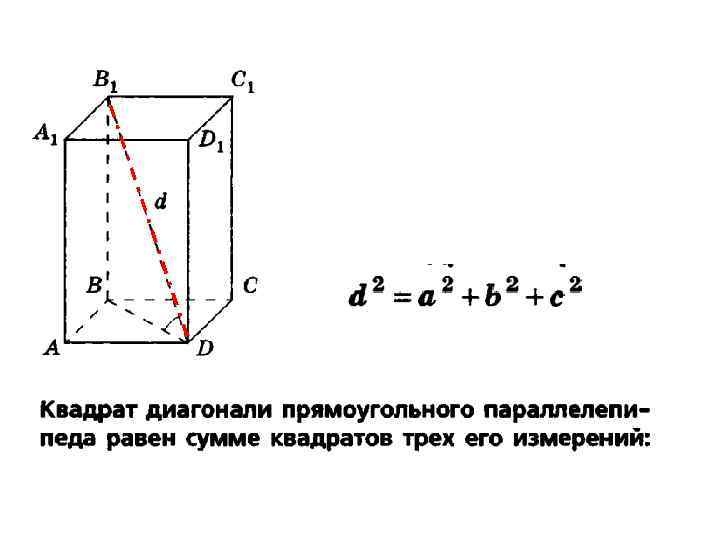
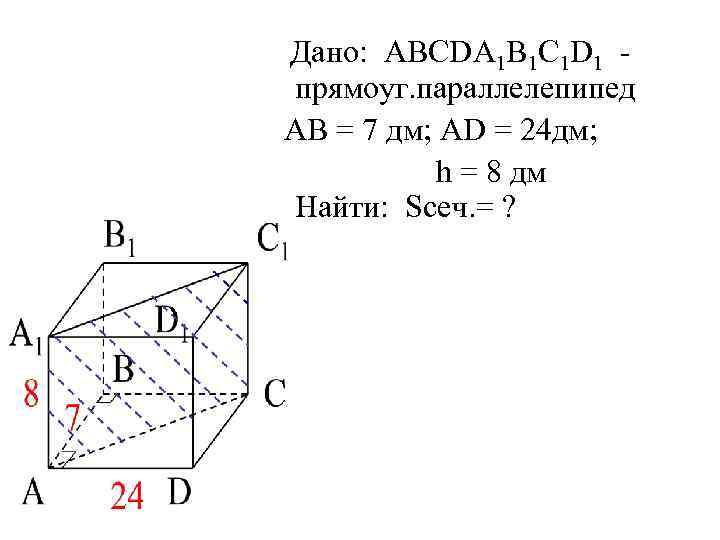Дано: АВСDА 1 В 1 С 1 D 1 прямоуг. параллелепипед АВ = 7 дм; АD = 24 дм; h = 8 дм Найти: Sсеч. = ?

Решение: Sсеч = S АА 1 С 1 С – прямоугольник; Sсеч = АС∙АА 1; АВСД – прямоугольник АС 2 = АВ 2 + ВС 2 Sсеч= 25∙ 8 = 200 дм 2 =2 м 2 Ответ: 2 м 2

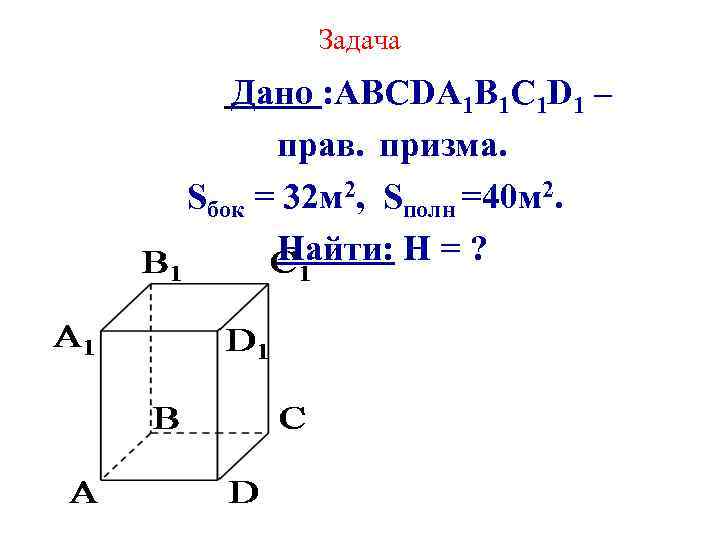Задача Дано : АВСDА 1 В 1 С 1 D 1 – прав. призма. Sбок = 32 м 2, Sполн =40 м 2. Найти: H = ?

Решение: Sбок = Р∙H ; Sполн. = Sбок+2 Sосн ; 2 Sосн = Sполн – Sбок; Sосн =( Sполн- Sбок): 2; Sосн =( 40 – 32) =4 м 2 Sосн = АD 2; => АD =2 м. ; Р = 4∙АD = 4∙ 2 = 8 ;

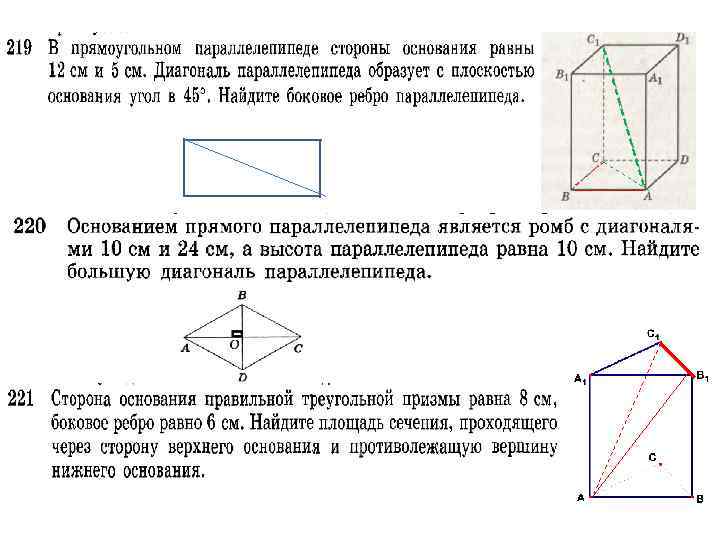
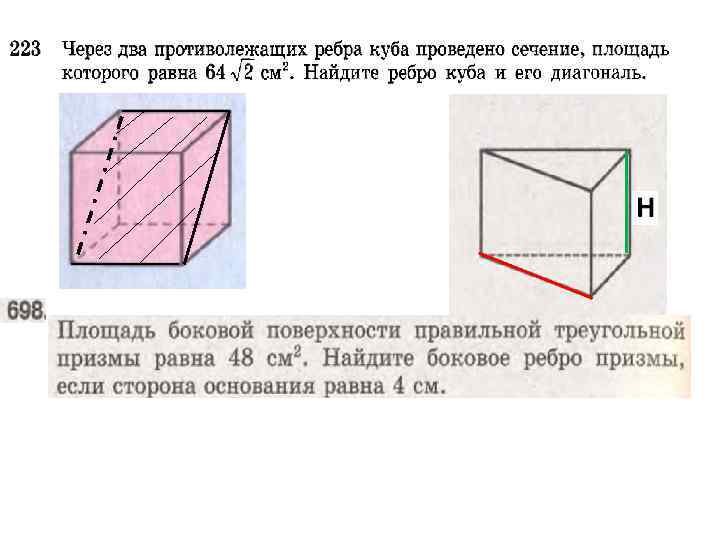
ДОМАШНЕЕ ЗАДАНИЕ • п. 27 - 31 , страница 67 • № 225, • № 226

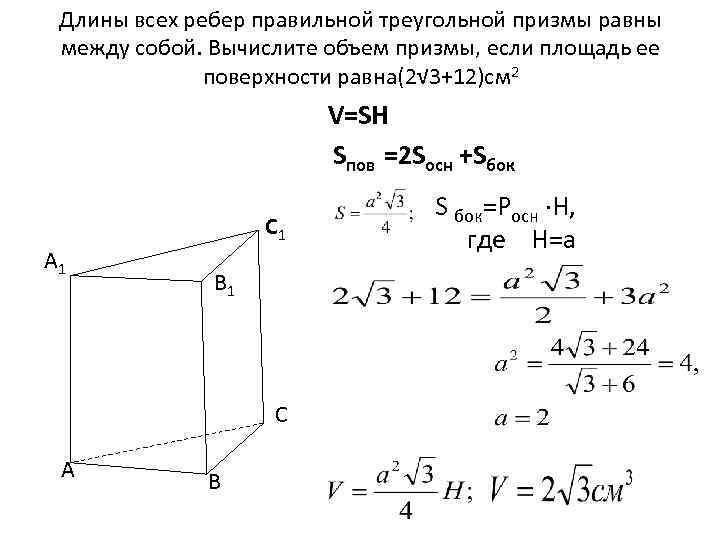Длины всех ребер правильной треугольной призмы равны между собой. Вычислите объем призмы, если площадь ее поверхности равна(2√ 3+12)cм 2 V=SH Sпов =2 Sосн +Sбок C 1 A 1 B 1 C А B S бок=Pосн ∙H, где H=a

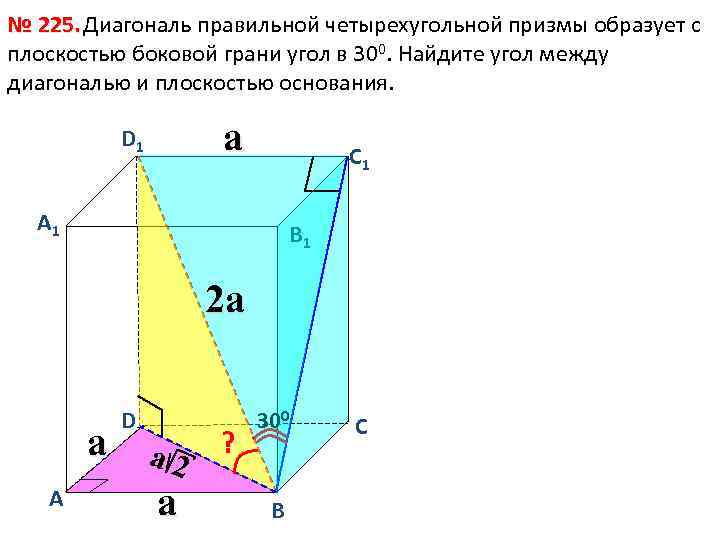№ 225. Диагональ правильной четырехугольной призмы образует с плоскостью боковой грани угол в 300. Найдите угол между диагональю и плоскостью основания. D 1 a С 1 А 1 В 1 2 a D А a a 2 a ? 300 В С

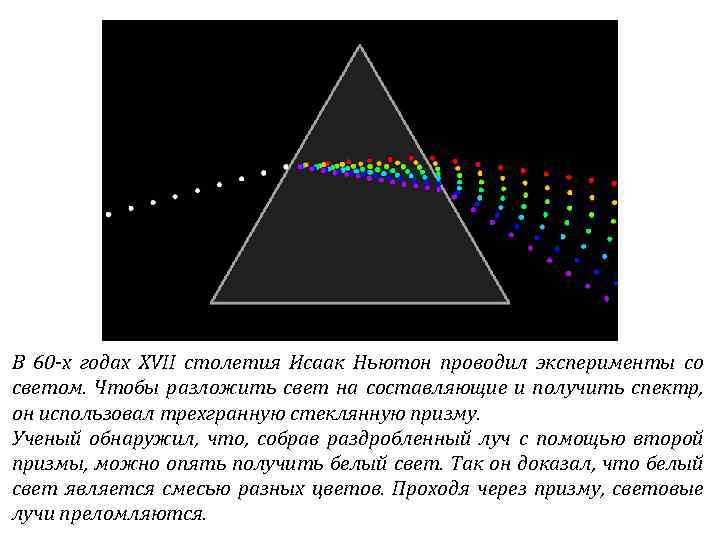В 60 -х годах ХVII столетия Исаак Ньютон проводил эксперименты со светом. Чтобы разложить свет на составляющие и получить спектр, он использовал трехгранную стеклянную призму. Ученый обнаружил, что, собрав раздробленный луч с помощью второй призмы, можно опять получить белый свет. Так он доказал, что белый свет является смесью разных цветов. Проходя через призму, световые лучи преломляются.

«Я затемнил мою комнату, − писал он, − и сделал очень маленькое отверстие в ставне для пропуска солнечного света» . На пути солнечного луча ученый поставил особое трехгранное стеклышко – призму. На противоположной стене он увидел разноцветную полоску – спектр. Ньютон объяснил это тем, что призма разложила белый цвет на составляющие его цвета. Ньютон первый разгадал, что солнечный луч многоцветный.

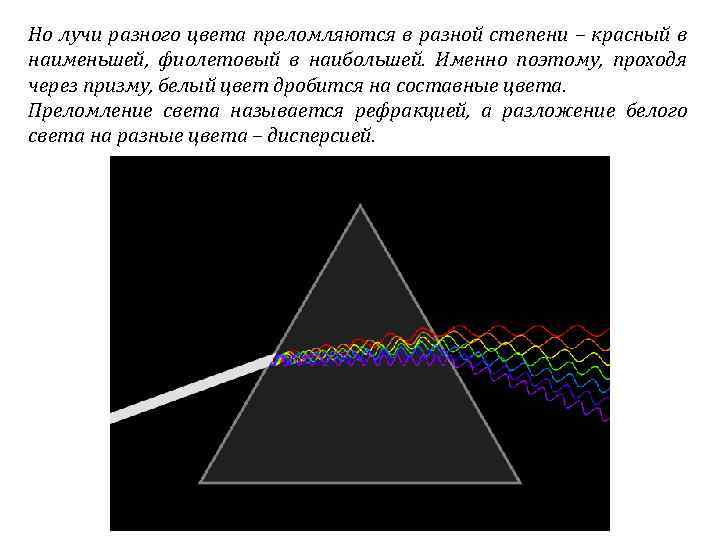Но лучи разного цвета преломляются в разной степени – красный в наименьшей, фиолетовый в наибольшей. Именно поэтому, проходя через призму, белый цвет дробится на составные цвета. Преломление света называется рефракцией, а разложение белого света на разные цвета – дисперсией.

Использование призмы для творческих фотоэффектов

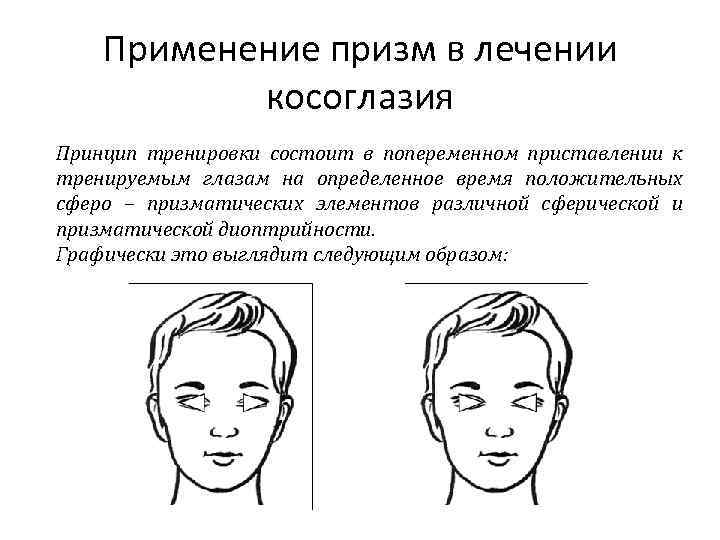Применение призм в лечении косоглазия Принцип тренировки состоит в попеременном приставлении к тренируемым глазам на определенное время положительных сферо – призматических элементов различной сферической и призматической диоптрийности. Графически это выглядит следующим образом:

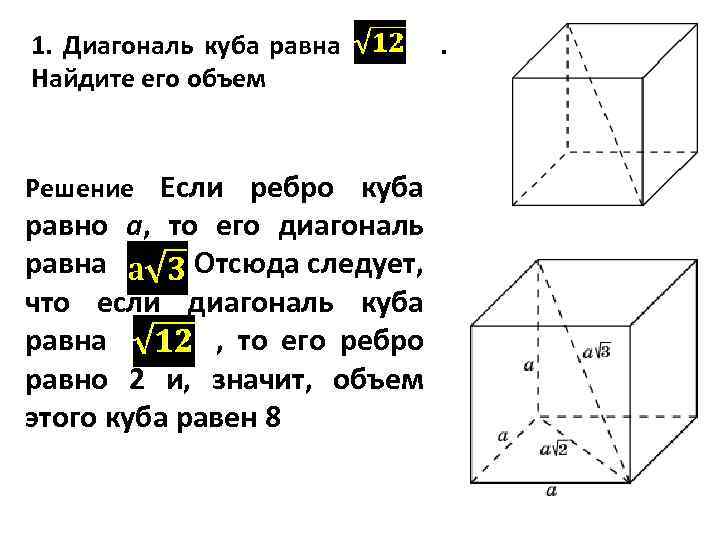1. Диагональ куба равна Найдите его объем Решение Если ребро куба равно a, то его диагональ равна. Отсюда следует, что если диагональ куба равна , то его ребро равно 2 и, значит, объем этого куба равен 8 .

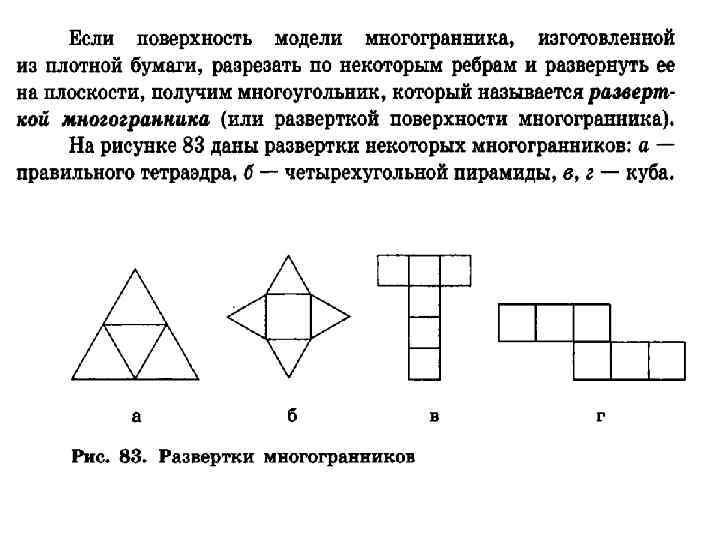
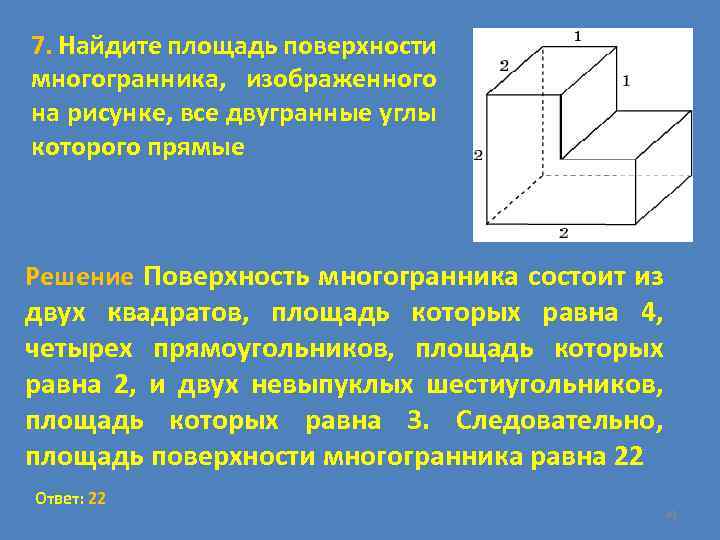7. Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого прямые Решение Поверхность многогранника состоит из двух квадратов, площадь которых равна 4, четырех прямоугольников, площадь которых равна 2, и двух невыпуклых шестиугольников, площадь которых равна 3. Следовательно, площадь поверхности многогранника равна 22 Ответ: 22 49