Приведение дробей к общему знаменателю
Основное свойство дроби Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь. Дроби можно приводить только к тем 4 2∙ 2 2 = которые 6 знаменателям, 3 ∙ 2 = кратны исходным. 3 2 3 = 4 6 = 6 9 = 8 12 =… 9 кратно 3 12 кратно 3
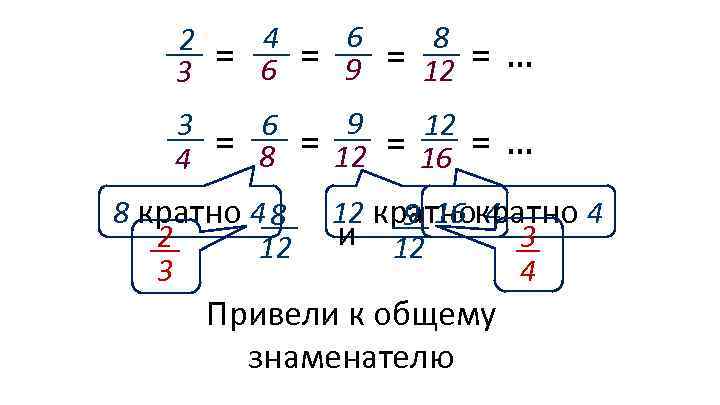
2 3 3 4 = 4 6 = 6 8 8 кратно 4 8 2 12 3 = 6 9 = 9 12 = 8 12 =… = 12 16 =… 12 кратно 4 9 16 4 и 12 3 4 Привели к общему знаменателю
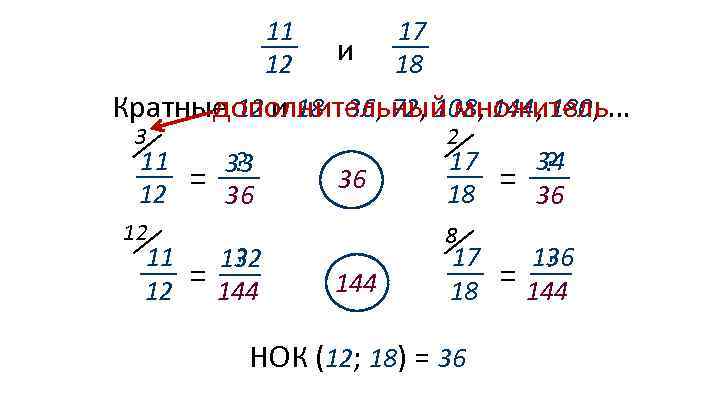
11 12 и 17 18 Кратные 12 и 18: 36, 72, 108, 144, 180, … дополнительный множитель 3 11 12 = 12 11 12 = ? 33 36 132 ? 144 2 36 17 18 = 34 ? 36 = 136 ? 144 8 144 17 18 НОК (12; 18) = 36
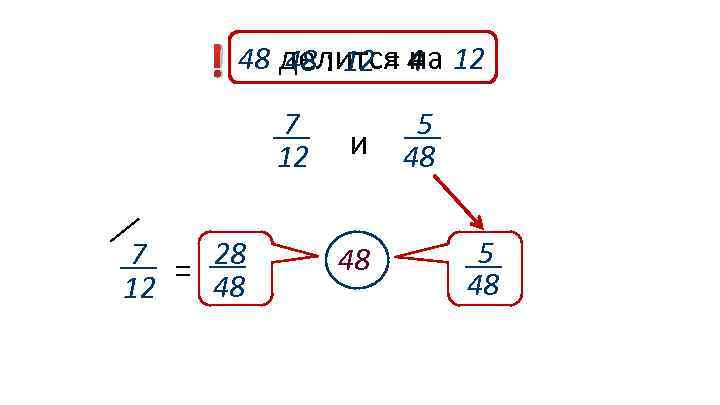
48 : 12 = на ! 48 делится 4 12 7 12 28 7 = 48 12 и 48 5 48
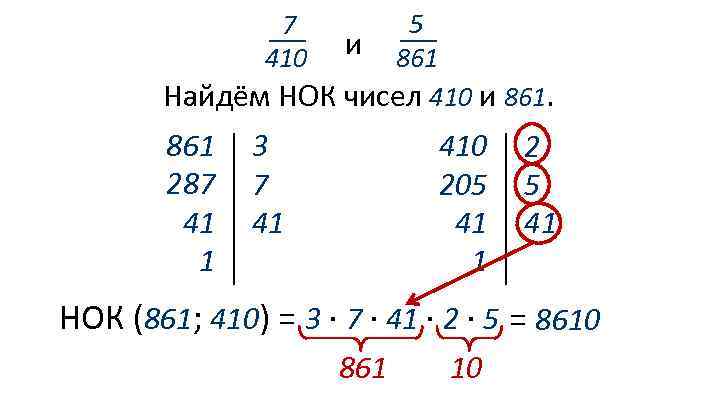
5 и 861 Найдём НОК чисел 410 и 861. 7 410 861 287 41 1 3 7 41 410 205 41 1 2 5 41 НОК (861; 410) = 3 ∙ 7 ∙ 41 ∙ 2 ∙ 5 = 8610 861 10
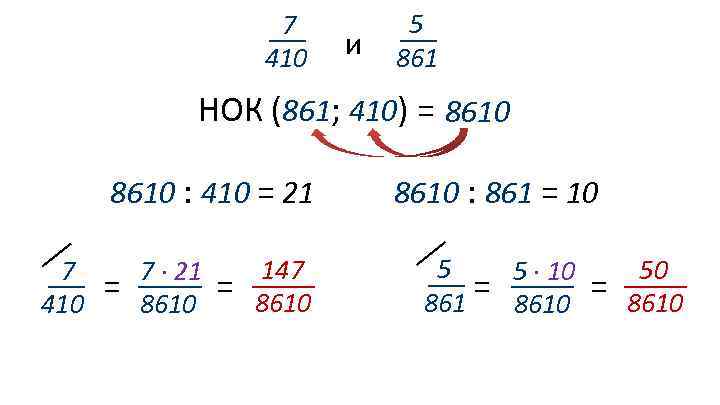
7 410 и 5 861 НОК (861; 410) = 8610 : 410 = 21 7 410 = 7 ∙ 21 8610 = 147 8610 : 861 = 10 5 5 ∙ 10 = 8610 861 = 50 8610
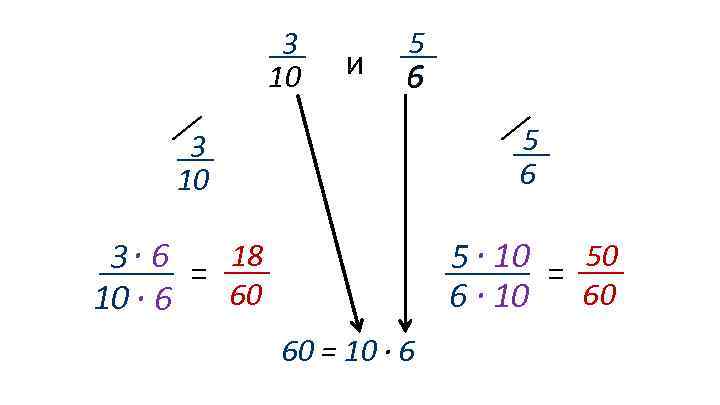
3 10 и 5 6 3 10 3 ∙ 6 = 18 60 10 ∙ 6 5 ∙ 10 = 50 60 6 ∙ 10 60 = 10 ∙ 6
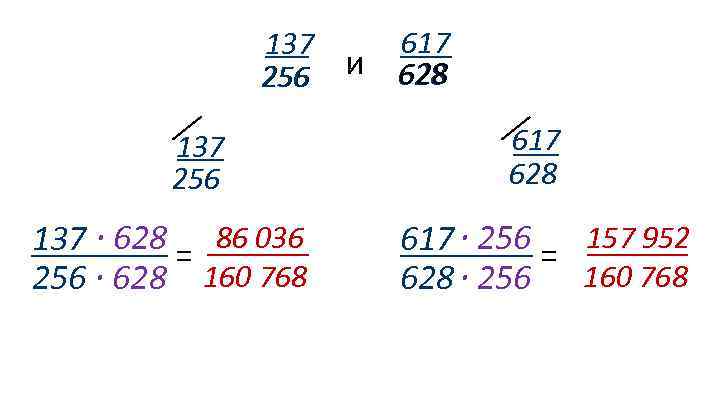
137 256 и 137 256 137 ∙ 628 = 86 036 256 ∙ 628 160 768 617 628 617 ∙ 256 = 157 952 628 ∙ 256 160 768
Любые две дроби можно привести к одному и тому же знаменателю, или, иначе, к общему знаменателю. Обычно дроби приводят к наименьшему общему знаменателю. Он равен наименьшему общему кратному знаменателей данных дробей.
Скачать презентацию Приведение дробей к общему знаменателю Основное свойство
10. Приведение дробей к общему знаменателю.pptx