Privacy Preserving Data Mining Lecture 3 Non-Cryptographic Approaches

Privacy Preserving Data Mining Lecture 3 Non-Cryptographic Approaches for Preserving Privacy (Based on Slides of Kobbi Nissim) Benny Pinkas HP Labs, Israel March 3, 2005 10 th Estonian Winter School in Computer Science 1

Why not use cryptographic methods? d … • Many users contribute data. Cannot require them to participate in a cryptographic protocol. – • In particular, cannot require p 2 p communication between users. Cryptographic protocols incur considerable overhead. March 3, 2005 10 th Estonian Winter School in Computer Science 2

Data Privacy d Data access mechanism March 3, 2005 10 th Estonian Winter School in Computer Science users breach privacy 3

Easy Tempting. Bad Solution A Solution Idea: a. Remove identifying information (name, SSN, …) b. Publish data Mr. Brown d Ms. John Mr. Doe But, ‘harmless’ attributes uniquely identify many patients (gender, age, approx weight, ethnicity, marital status…) • Recall, DOB+gender+zip code identify people whp. • Worse: `rare’ attributes (e. g. disease with prob. 1/3000) • March 3, 2005 10 th Estonian Winter School in Computer Science 4

What is Privacy? • Something should not be computable from query answers E. g. Joe={Joe’s private data} – The definition should take into account the adversary’s power (computational, #of queries, prior knowledge, …) – • Quite often it is much easier to say what is surely nonprivate – March 3, 2005 Intuition: privacy breached able to E. g. Strong breaking of privacy: adversary is if it is possible to compute retrieve (almost) everybody’s private data someone’s private information from his identity 10 th Estonian Winter School in Computer Science 5

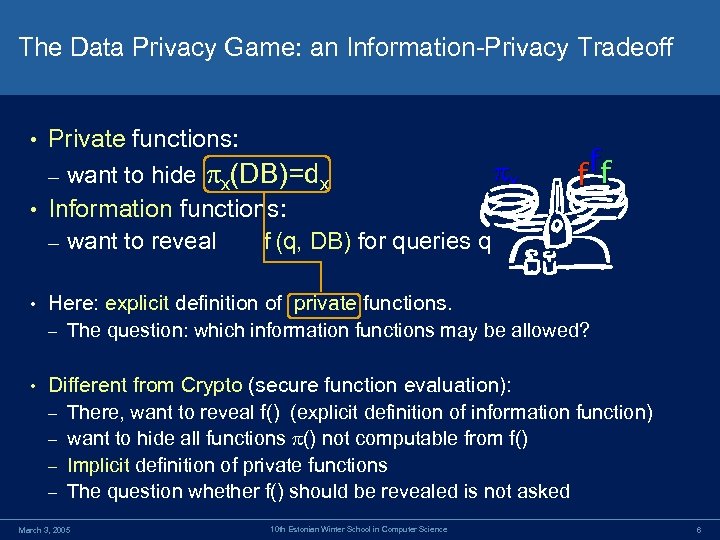The Data Privacy Game: an Information-Privacy Tradeoff Private functions: x – want to hide x(DB)=dx • Information functions: – want to reveal f (q, DB) for queries q • ff f • Here: explicit definition of private functions. – The question: which information functions may be allowed? • Different from Crypto (secure function evaluation): – There, want to reveal f() (explicit definition of information function) – want to hide all functions () not computable from f() – Implicit definition of private functions – The question whether f() should be revealed is not asked March 3, 2005 10 th Estonian Winter School in Computer Science 6

A simplistic model: Statistical Database (SDB) query Mr. Fox 0/1 d {0, 1}n q [n] Ms. John 0/1 answer aq= i q di Mr. Doe 0/1 bits March 3, 2005 10 th Estonian Winter School in Computer Science 7

Approaches to SDB Privacy • • Studied extensively since the 70 s Perturbation – – Add randomness. Give `noisy’ or `approximate’ answers Techniques: • Data perturbation (perturb data and then answer queries as usual) [Reiss 84, Liew Choi Liew 85, Traub Yemini Wozniakowski 84] … • Output perturbation (perturb answers to queries) [Denning 80, Beck 80, Achugbue Chin 79, Fellegi Phillips 74] … – • Recent interest: [Agrawal, Srikant 00] [Agrawal, Aggarwal 01], … Query Restriction – – Answer queries accurately but sometimes disallow queries Require queries to obey some structure [Dobkin Jones Lipton 79] • Restricts number of queries – March 3, 2005 Auditing [Chin Ozsoyoglu 82, Kleinberg Papadimitriou Raghavan 01] 10 th Estonian Winter School in Computer Science 8

Some Recent Privacy Definitions X – data, Y – (noisy) observation of X [Agrawal, Srikant ‘ 00] Interval of confidence – Let Y = X+noise (e. g. uniform noise in [-100, 100]. – Perturb input data. Can still estimate underlying distribution. – Tradeoff: more noise less accuracy but more privacy. – Intuition: large possible interval privacy preserved • Given Y, we know that within c% confidence X is in [a 1, a 2]. For example, for Y=200, with 50% X is in [150, 250]. • a 2 -a 1 defines the amount of privacy at c% confidence – Problem: there might be some a-priori information about X • X = someone’s age & Y= -97 March 3, 2005 10 th Estonian Winter School in Computer Science 9

The [AS] scheme can be turned against itself • Assume that N is large – Even if the data-miner doesn’t have a-priori information about X, it can estimate it given the randomized data Y. • The perturbation is uniform in [-1, 1] • [AS]: privacy interval 2 with confidence 100% • Let fx(X)=50% for x [0, 1], and 50% for x [4, 5]. • But, after learning fx(X) the value of X can be easily localized within an interval of size at most 1. – Problem: aggregate information provides information that can be used to attack individual data March 3, 2005 10 th Estonian Winter School in Computer Science 10

Some Recent Privacy Definitions X – data, Y – (noisy) observation of X • [Agrawal, Aggarwal ‘ 01] Mutual information – Intuition: • High entropy is good. I(X; Y) = H(X)-H(X|Y) (mutual information) • small I(X; Y) (mutual information) privacy preserved (Y provides little information about X). • Problem [EGS] : Average notion. Privacy loss can happen with low but significant probability, but without affecting I(X; Y). – Sometimes I(X; Y) seems good but privacy is breached – March 3, 2005 10 th Estonian Winter School in Computer Science 11

Output Perturbation (Randomization Approach) • Exact answer to query q: – aq = i q di • Actual SDB answer: âq • Perturbation : – For • all q: | âq – aq | ≤ Questions: Does perturbation give any privacy? – How much perturbation is needed for privacy? – Usability – March 3, 2005 10 th Estonian Winter School in Computer Science 12

Privacy Preserved by Perturbation n Database: d R{0, 1}n (uniform input distribution!) âq Algorithm: on query q, 1. Let aq= i q di q/2 2. If | aq - |q|/2 | < return âq = |q| / 2 3. Otherwise return âq = aq q/2 aq 2 Privacy is preserved n (lgn) – Assume poly(n) queries – If n (lgn)2, whp always use rule 2 • No information about d is given! • (but database is completely useless…) • Shows that sometimes perturbation n is enough for privacy. Can we do better? March 3, 2005 10 th Estonian Winter School in Computer Science 13

Perturbation << n Implies no Privacy • The previous useless database achieves the best possible perturbation. • Theorem [Dinur-Nissim]: Given any DB and any DB response algorithm with perturbation = o( n), there is a poly-time reconstruction algorithm that outputs a database d’, s. t. dist(d, d’) < o(n). strong breaking of privacy March 3, 2005 10 th Estonian Winter School in Computer Science 14

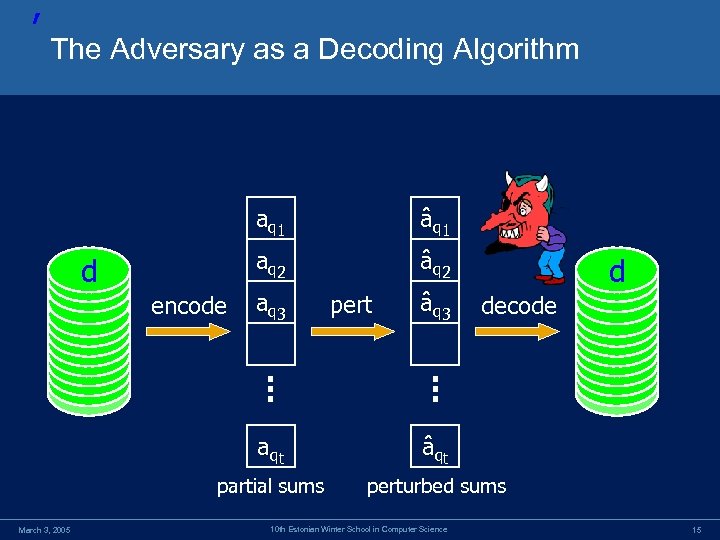’ The Adversary as a Decoding Algorithm a q 1 a q 2 d encode â q 1 â q 2 a q 3 pert â q 3 d decode a qt partial sums March 3, 2005 â qt perturbed sums 10 th Estonian Winter School in Computer Science 15

Proof of Theorem [DN 03] The Adversary Reconstruction Algorithm • Query phase: Get âqj for t random subsets q 1, …, qt • Weeding phase: Solve the Linear Program (over ): 0 xi 1 | i qj xi - âqj | • Rounding: Let ci = round(xi), output c Observation: A solution always exists, e. g. x=d. March 3, 2005 10 th Estonian Winter School in Computer Science 16

Why does the Reconstruction Algorithm Work? • Consider x {0, 1}n s. t. dist(x, d)=c·n = (n) • Observation: – – The differences in the sum of these coordinates is, with constant probability, at least ( n) (> = o( n) ). – • A random q contains c’·n coordinates in which x≠d Such a q disqualifies x as a solution for the LP Since the total number of queries q is polynomial, then all such vectors x are disqualified with overwhelming probability. March 3, 2005 10 th Estonian Winter School in Computer Science 17

Summary of Results (statistical database) small DB – Unlimited adversary: • Perturbation of magnitude (n) required medium DB [Dinur, Nissim 03] : – Polynomial-time adversary: • Perturbation of magnitude (sqrt(n)) is required (shown above) – In both cases, adversary may reconstruct a good approximation for the database • Disallows even very weak notions of privacy large DB • – Bounded adversary, restricted to T << n queries (Su. LQ): • There is a privacy preserving access mechanism with perturbation << sqrt(T) • Chance for usability • Reasonable model as database grows larger and larger March 3, 2005 10 th Estonian Winter School in Computer Science 18

Su. LQ for Multi-Attribute Statistical Database (SDB) Database {di, j} Row distribution D (D 1, D 2, …, Dn) k attributes n persons 0 0 0 1 1 0 Query (q, f) q [ n] Answer aq, f= i q f(di) f : {0, 1}k {0, 1} f f f aq, f 1 0 0 1 1 f 0 0 1 March 3, 2005 10 th Estonian Winter School in Computer Science 19

Privacy and Usability Concerns for the Multi-Attribute Model [DN] Rich set of queries: subset sums over any property of the k attributes – Obviously increases usability, but how is privacy affected? • More to protect: functions of the k attributes • Relevant factors: – What is the adversary’s goal? – Row dependency • Vertically split data (between k or less databases): – Can privacy still be maintained with independently operating databases? • March 3, 2005 10 th Estonian Winter School in Computer Science 20

Privacy Definition - Intuition • 3 -phase adversary – Phase 0: defines a target set G of poly(n) functions g: {0, 1}k {0, 1} • Will try to learn some of this information about someone Phase 1: adaptively queries the database T=o(n) times – Phase 2: chooses an index i of a row it intends to attack and a function g G use all – • Attack: – given d-i – try to guess g(di, 1…di, k) March 3, 2005 10 th Estonian Winter School in Computer Science gained info to choose i, g 21

The Privacy Definition • • P 0 i, g – a-priori probability that g(di, 1…di, k)=1 p Ti, g – a-posteriori probability that g(di, 1…di, k)=1 – • Given answers to the T queries, and d-i Define conf(p) = log (p/(1 -p)) – – 1 -1 relationship between p and conf(p) conf(1/2)=0; conf(2/3)=1; conf(1)= • conf i, g = conf(p. Ti, g) – conf(p 0 i, g) • ( , T) – privacy: (“relative privacy”) – March 3, 2005 For all distributions D 1…Dn , row i, function g and any adversary making at most T queries: Pr[ conf i, g > ] = neg(n) 10 th Estonian Winter School in Computer Science 22

The Su. LQ* Database Adversary restricted to T << n queries • On query (q, f): • • q [n] • f : {0, 1}k {0, 1} (binary function) aq, f = i q f(di, 1…di, k) – Let N Binomial(0, T ) – Return aq, f+N – Let *Su. LQ – Sub Linear Queries March 3, 2005 10 th Estonian Winter School in Computer Science 23

Privacy Analysis of the Su. LQ Database • Pmi, g - a-posteriori probability that g(di, 1…di, k)=1 – • Given d-i and answers to the first m queries conf(pmi, g) Describes a random walk on the line with: Starting point: conf(p 0 i, g) – Compromise: conf(pmi, g) – conf(p 0 i, g) > – • W. h. p. more than T steps needed to reach compromise conf(p 0 i, g) March 3, 2005 10 th Estonian Winter School in Computer Science conf(p 0 i, g) + 24

Usability: One multi-attribute Su. LQ DB • Statistics of any property f of the k attributes I. e. for what fraction of the (sub)population does f(d 1…dk) hold? – Easy: just put f in the query – Other applications: • k independent multi-attribute Su. LQ DBs • Vertically partitioned Sul. Q DBs • Testing whether Pr[ | ] ≥ Pr[ ]+ – Caveat: we hide g() about a specific row (not about multiple rows) – March 3, 2005 10 th Estonian Winter School in Computer Science 0 1 0 1 1 1 0 1 1 0 0 1 25

Overview of Methods • Input Perturbation Query SDB • Data Perturbation SDB’ User Response Output Perturbation (Restricted) Query SDB • Perturbed Response User Query Restriction (Restricted) Query SDB March 3, 2005 Exact Response Or Denial 10 th Estonian Winter School in Computer Science User 26

Query restriction (Restricted) Query User SDB • Exact Response Or Denial The decision whether to answer or deny the query Can be based on the content of the query and on answers to previous queries – Or, can be based on the above and on the content of the database – March 3, 2005 10 th Estonian Winter School in Computer Science 27

Auditing • [AW 89] classify auditing as a query restriction method: – “Auditing of an SDB involves keeping up-to-date logs of all queries made by each user (not the data involved) and constantly checking for possible compromise whenever a new query is issued” • Partial motivation: May allow for more queries to be posed, if no privacy threat occurs. Early work: Hofmann 1977, Schlorer 1976, Chin, Ozsoyoglu 1981, 1986 • Recent interest: Kleinberg, Papadimitriou, Raghavan 2000, Li, • Wang, Jajodia 2002, Jonsson, Krokhin 2003 March 3, 2005 10 th Estonian Winter School in Computer Science 28

How Auditors may Inadvertently Compromise Privacy March 3, 2005 10 th Estonian Winter School in Computer Science 29

The Setting q = (f , i 1, …, ik) f (di 1, …, dik) • Dataset: d={d 1, …, dn} – • Statistical database Entries di: Real, Integer, Boolean Query: q = (f , i 1, …, ik) – f : Min, Max, Median, Sum, Average, Count… Bad users will try to breach the privacy of individuals • Compromise uniquely determine di (very weak def) • March 3, 2005 10 th Estonian Winter School in Computer Science 30

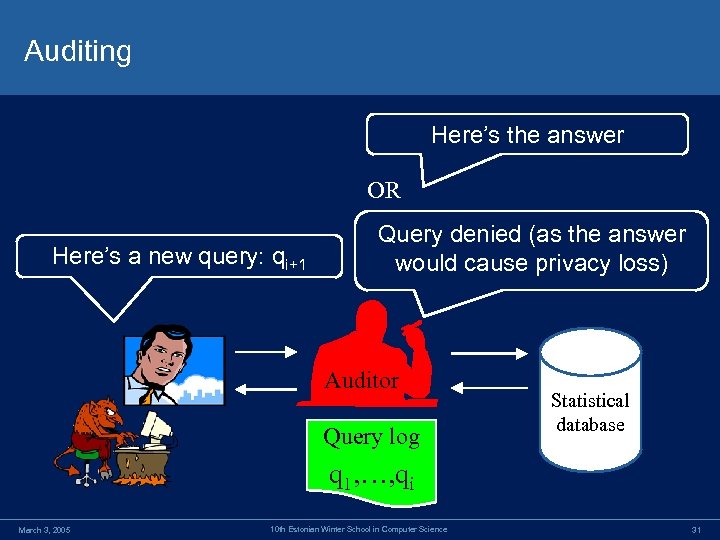Auditing Here’s the answer OR Here’s a new query: qi+1 Query denied (as the answer would cause privacy loss) Auditor Query log Statistical database q 1, …, qi March 3, 2005 10 th Estonian Winter School in Computer Science 31

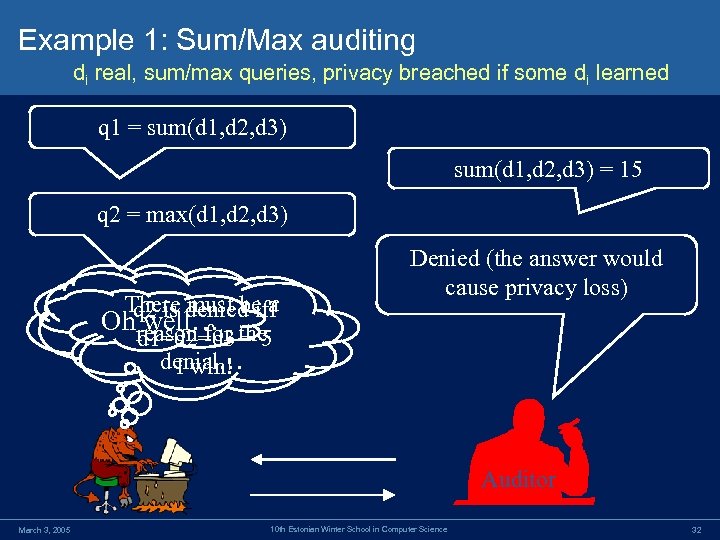Example 1: Sum/Max auditing di real, sum/max queries, privacy breached if some di learned q 1 = sum(d 1, d 2, d 3) = 15 q 2 = max(d 1, d 2, d 3) There denied iff q 2 is must be a Ohreason for the well… d 1=d 2=d 3 = 5 denial… I win! Denied (the answer would cause privacy loss) Auditor March 3, 2005 10 th Estonian Winter School in Computer Science 32

Sounds Familiar? David Duncan, Former auditor for Enron and partner in Andersen: Mr. Chairman, I would like to answer the committee's questions, but on the advice of my counsel I respectfully decline to answer the question based on the protection afforded me under the Constitution of the United States. March 3, 2005 10 th Estonian Winter School in Computer Science 33

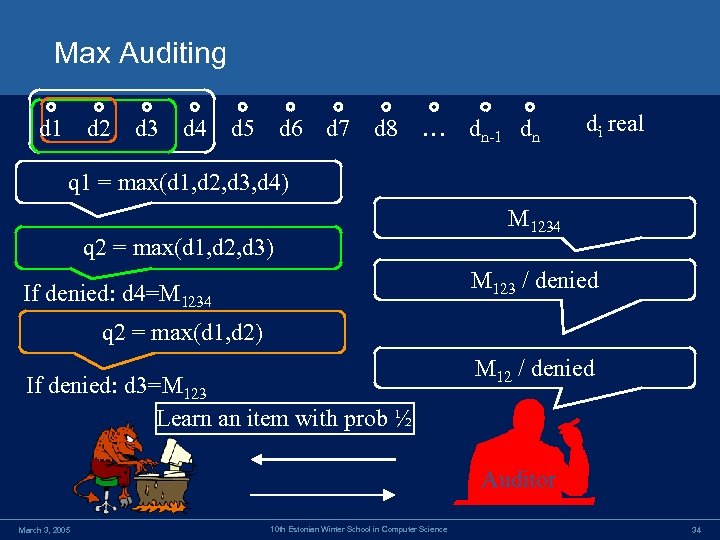Max Auditing d 1 d 2 d 3 d 4 d 5 d 6 d 7 d 8 … dn-1 dn di real q 1 = max(d 1, d 2, d 3, d 4) q 2 = max(d 1, d 2, d 3) M 1234 M 123 / denied If denied: d 4=M 1234 q 2 = max(d 1, d 2) If denied: d 3=M 123 Learn an item with prob ½ M 12 / denied Auditor March 3, 2005 10 th Estonian Winter School in Computer Science 34

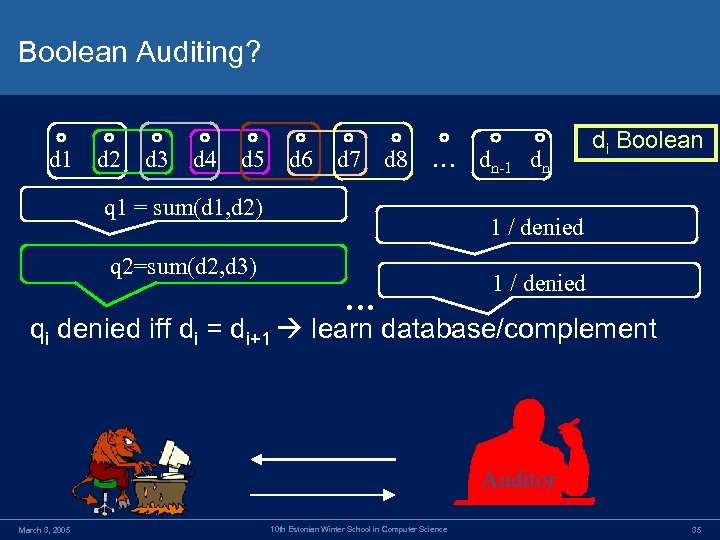Boolean Auditing? d 1 d 2 d 3 d 4 d 5 d 6 d 7 d 8 … dn-1 dn q 1 = sum(d 1, d 2) di Boolean 1 / denied q 2=sum(d 2, d 3) … 1 / denied qi denied iff di = di+1 learn database/complement Auditor March 3, 2005 10 th Estonian Winter School in Computer Science 35

The Problem • The problem: – Query denials leak (potentially sensitive) information • Users cannot decide denials by themselves Possible assignments to {d 1, …, dn} Assignments consistent with (q 1, …qi, a 1, …, ai) qi+1 denied March 3, 2005 10 th Estonian Winter School in Computer Science 36

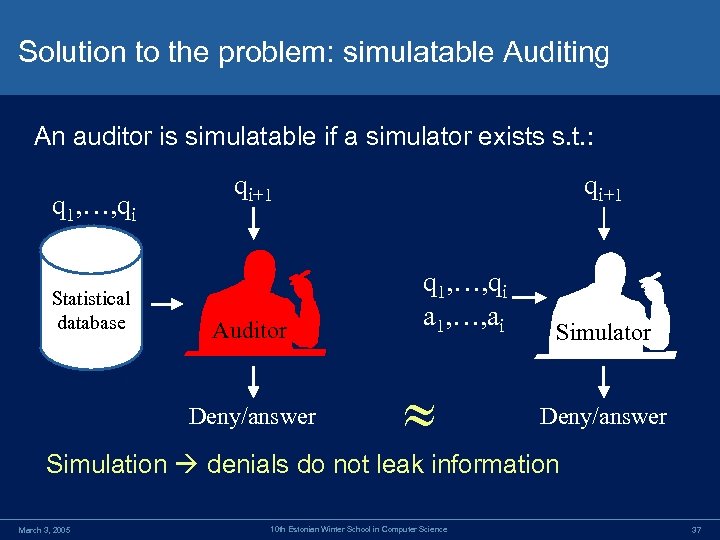Solution to the problem: simulatable Auditing An auditor is simulatable if a simulator exists s. t. : q 1, …, qi Statistical database qi+1 Auditor Deny/answer qi+1 q 1, …, qi a 1, …, ai Simulator Deny/answer Simulation denials do not leak information March 3, 2005 10 th Estonian Winter School in Computer Science 37

Why Simulatable Auditors do not Leak Information? Possible assignments to {d 1, …, dn} Assignments consistent with (q 1, …qi, a 1, …, ai ) qi+1 denied/allowed March 3, 2005 10 th Estonian Winter School in Computer Science 38

Simulatable auditing March 3, 2005 10 th Estonian Winter School in Computer Science 39

Query Restriction for Sum Queries • Given: – D={x 1, . . , xn} dataset, xi – S is a subset of X. Query: xi S xi • Is it possible to compromise D? – Here compromise means: uniquely determine xi from the queries • Can compromise if subsets arbitrarily small: – sum(x 9)= x 9 March 3, 2005 10 th Estonian Winter School in Computer Science 40

Query Set Size Control Do not permit queries that involve a small subset of the database. • Compromise still possible • – Want to discover x: sum(x, y 1, . . , yk) - sum(y 1, . . , yk) = x Issue: Overlap • In general, overlap is not enough. • Need to restrict also the number of queries – Note that overlap itself sometimes restricts number of queries (e. g. size of queries = cn, overlap = const, only about 1/c possible queries) – March 3, 2005 10 th Estonian Winter School in Computer Science 41

Restricting Set-Sum Queries • Restricting the sum queries based on Number of database elements in the sum – Overlap with previous sum queries – Total number of queries – • Note that the criteria are known to the user – • They do not depend on the contents of the database Therefore, the user can simulate the denial/no-denial answer given by the DB – Simulatable auditing March 3, 2005 10 th Estonian Winter School in Computer Science 42

Restricting Overlap and Number of Queries • Assume: – |Query Qi| ≥ k – |Qi Qj| ≤ r – Adversary knows a-priori at most L values, L+1 < k • Claim: Data cannot be compromised with fewer than 1+(2 k-L)/r Sum Queries. 1 0 0 0 1 1 2 1 0 0 1 0 x 1 x 2 x 3. . = Q 1 Q 2 Q 3. . . ≥k ≥k xl ≤r xn March 3, 2005 ≤r ≤r Qt ≥k 10 th Estonian Winter School in Computer Science ≥k 43

Overlap + Number of Queries Claim: Data cannot be compromised with fewer than 1+(2 k-L)/r Sum Queries [Dobkin, Jones, Lipton][Reiss] – • Suppose xc compromised after t queries where each query represented by: – • k < query size, r > overlap, L a-priori known items Qi = xi 1 + xi 2 + … + xik for i =1, …, t Implies that: xc = i=1, t i Qi = i=1, t i j=1, k xij – Let i = 1 if x in query i, 0 otherwise – xc= i=1, t i =1, n i x = =1, n ( i=1, t i i )x – March 3, 2005 10 th Estonian Winter School in Computer Science 44

Overlap + Number of Queries We have: xc= =1, n ( i=1, t i i )x • In the above sum, ( i=1, t i i ) must be 0 for all x except for xc (in order for xc to be compromised) • This happens iff i =0 for all i, or if i = j =1 and i j have opposite signs – or i =0, in which case the ith query didn’t matter March 3, 2005 10 th Estonian Winter School in Computer Science 45

Overlap + Number of Queries • • • Wlog, first query contains xc, second query is of opposite sign. In the first query, k elements are probed The second query adds at least k-r elements Elements from first and second queries cannot be canceled within the same (additional) query (opposite signs requires) Therefore each new query cancels items from first or from second query, but not from both. Need to cancel 2 k-r-L elements. – Need 2+(2 k-r-L)/r queries, i. e. 1+(2 k-L)/r. March 3, 2005 10 th Estonian Winter School in Computer Science 46

Notes • The number of queries satisfying |Qi|≥ k and |Qi Qj| ≤r is small If k=n/c for some constant c and r=const, then there are only ~c queries where no two queries overlap by more than 1. – Hence , query sequence length may be uncomfortably short. – Or, if r=k/c (overlap is a constant fraction of query size) then number of queries, 1+(2 k-L)/r, is O( c). – March 3, 2005 10 th Estonian Winter School in Computer Science 47

Conclusions Privacy should be defined analyzed rigorously – In particular, assuming randomization privacy is dangerous • High perturbation is needed for privacy against polynomial adversaries – Threshold phenomenon – above n: total privacy, below n: no privacy (for poly-time adversary) – Main tool: a reconstruction algorithm • Careless auditing might leak private information • Self Auditing (simulatable auditors) is safe – Decision whether to allow a query based on previous `good’ queries and their answers • • Without access to DB contents • Users may apply the decision procedure by themselves March 3, 2005 10 th Estonian Winter School in Computer Science 48

To. Do • Come up with good model and requirements for database privacy – Learn from crypto – Protect against more general loss of privacy • Simulatable auditors are a starting point for designing more reasonable audit mechanisms March 3, 2005 10 th Estonian Winter School in Computer Science 49

References • Course web page: A Study of Perturbation Techniques for Data Privacy, Cynthia Dwork and Nina Mishra and Kobbi Nissim, http: //theory. stanford. edu/~nmishra/cs 369 -2004. html – Privacy and Databases http: //theory. stanford. edu/~rajeev/privacy. html – March 3, 2005 10 th Estonian Winter School in Computer Science 50

Foundations of CS at the Weizmann Institute • • • Uri Feige Oded Goldreich Shafi Goldwasser David Harel Moni Naor • • • David Peleg Amir Pnueli Ran Raz Omer Reingold Adi Shamir Yellow crypto • All students receive a fellowship • Language of instruction English March 3, 2005 10 th Estonian Winter School in Computer Science 51