Privacy Preserving Data Mining Lecture 2 Cryptographic Solutions

Privacy Preserving Data Mining Lecture 2 Cryptographic Solutions Benny Pinkas HP Labs, Israel March 1, 2005 10 th Estonian Winter School in Computer Science 1

Secure two-party computation - definition Input: Output: As if… y x F(x, y) and nothing else y x F(x, y) March 1, 2005 10 th Estonian Winter School in Computer Science F(x, y) 2

Secure Function Evaluation A major topic of cryptographic research • How to let n parties, P 1, . . , Pn compute a function F(x 1, . . , xn) • Where input xi is known to party Pi – Parties learn the final input and nothing else – • Caveat: cryptographic definitions of secure computation are both too strong and too weak: Too strong: do not allow leakage of harmless information; the price of this extra security is in efficiency. – Too weak: do not address leakage or misuse caused by the function itself (e. g. , information implied by the outputs, or misbehavior in choosing an input). – March 1, 2005 10 th Estonian Winter School in Computer Science 3

Secure Function Evaluation • Major Result [Yao]: “Any function that can be evaluated using polynomial resources can be securely evaluated using polynomial resources” (under some cryptographic assumption) March 1, 2005 10 th Estonian Winter School in Computer Science 5

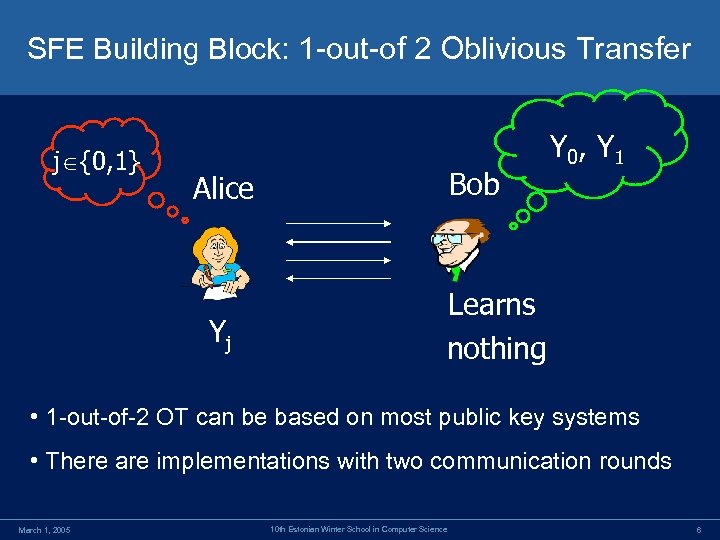SFE Building Block: 1 -out-of 2 Oblivious Transfer j {0, 1} Bob Alice Yj Y 0 , Y 1 Learns nothing • 1 -out-of-2 OT can be based on most public key systems • There are implementations with two communication rounds March 1, 2005 10 th Estonian Winter School in Computer Science 6

General Two party Computation Two party protocol • Input: – Sender: Function F (some representation) • The sender’s input Y is already embedded in F – Receiver: • X 0, 1 n Output: – Receiver: F(x) and nothing else about F – Sender: nothing about x March 1, 2005 10 th Estonian Winter School in Computer Science 7

Representations of F • • • Boolean circuits [Yao, GMW, …] Algebraic circuits [BGW, …] Low deg polynomials [BFKR] Matrices product over a large field [FKN, IK] Randomizing polynomials [IK] Communication Complexity Protocol [NN] March 1, 2005 10 th Estonian Winter School in Computer Science 8

Secure two-party computation of general functions [Yao] • First, represent the function F as a Boolean circuit C – It’s always possible – Sometimes it’s easy (additions, comparisons) – Sometimes the result is inefficient (e. g. for indirect addressing, e. g. A[x] ) • Then, “garble” the circuit • Finally, evaluate the garbled circuit March 1, 2005 10 th Estonian Winter School in Computer Science 9

Garbling the circuit • Bob constructs the circuit, and then garbles it. W values will serve as cryptographic keys wk 0, wk 1 G wi 0, wi 1 March 1, 2005 w. J 0, w. J 1 10 th Estonian Winter School in Computer Science Wk 0 0 on wire k Wk 1 1 on wire k (Alice will learn one string per wire, but not which bit it corresponds to. ) 10

Gate tables • For every gate, every combination of input values is used as a key for encrypting the corresponding output • Assume G=AND. Bob constructs a table: Encryption of wk 0 using keys wi 0, w. J 0 – Encryption of wk 0 using keys wi 0, w. J 1 – Encryption of wk 0 using keys wi 1, w. J 0 – Encryption of wk 1 using keys wi 1, w. J 1 – • March 1, 2005 (AND(0, 0)=0) (AND(0, 1)=0) (AND(1, 0)=0) (AND(1, 1)=1) Result: given wix, w. Jy, can compute wk. G(x, y) 10 th Estonian Winter School in Computer Science 11

Secure computation Bob sends the table of gate G to Alice • Given, e. g. , wi 0, w. J 1, Alice computes wk 0 by decrypting the corresponding entry in the table, but she does not know the actual values of the wires. • Encryption of wk 0 using keys wi 0, w. J 0 wk 0, wk 1 Encryption of wk 0 using keys wi 0, w. J 1 Encryption of wk 1 using keys wi 1, w. J 1 G Encryption of wk 0 using keys wi 1, w. J 0 Permuted order March 1, 2005 wi 0, wi 1 10 th Estonian Winter School in Computer Science w. J 0, w. J 1 12

Secure computation • Bob sends to Alice – Tables encoding each circuit gate. – Garbled values (w’s) of his input values. – Translation from garbled values of output wires to actual 0/1 values. • March 1, 2005 If Alice gets garbled values (w’s) of her input values, she can compute the output of the circuit, and nothing else. 10 th Estonian Winter School in Computer Science 13

Alice’s input • For every wire i of Alice’s input: – The parties run an OT protocol – Alice’s input is her input bit (s). – Bob’s input is wi 0, wi 1 – Alice learns wis The OTs for all input wires can be run in parallel. • Afterwards Alice can compute the circuit by herself. • March 1, 2005 10 th Estonian Winter School in Computer Science 14

Secure computation – the big picture • • • Represent the function as a circuit C Bob sends to Alice 4|C| encryptions (e. g. 64|C| Bytes), 4 encryptions for every gate. Alice performs an OT for every input bit. (Can do, e. g. 100 -1000 OTs per sec. ) ~One round of communication. Efficient for medium size circuits! March 1, 2005 10 th Estonian Winter School in Computer Science 15

Example • The Millionaires problem: comparing two N bit numbers • What’s the overhead? March 1, 2005 10 th Estonian Winter School in Computer Science 16

Applications • • • Two parties. Two large data sets. Max? Mean? Median? Intersection? Decision Tree learning? ID 3? March 1, 2005 10 th Estonian Winter School in Computer Science 17

Fairplay – a secure two-party computation system Malkhi, Nissan, P. , Sella • A a full fledged secure two-party computation system, implementing Yao’s “garbled circuit” protocol. • Goals: – – – Investigate whether two-party SFE is practical Actual measurements of overall computation Breakdown of computation into parts Computation versus communication? Test-bed for various optimizations March 1, 2005 10 th Estonian Winter School in Computer Science 18

Fairplay • The Compilation paradigm – Programs written in SFDL, a high-level programming language – Allows clear, formal, easily understandable definition and requirements by humans SHDL: Low-level language describing Boolean circuits – SFDL SHDL compiler and optimizer – SHDL Java programs implementing Yao’s protocol – March 1, 2005 10 th Estonian Winter School in Computer Science 19

Fairplay – SFDL example program Millionaires { type int = Int<20>; // 20 -bit integer type Alice. Input = int; type Bob. Input = int; type Alice. Output = Boolean; type Bob. Output = Boolean; type Output = struct {Alice. Output alice, Bob. Output bob}; type Input = struct {Alice. Input alice, Bob. Input bob}; function Output output(Input input) { output. alice = input. alice > input. bob; output. bob = input. bob > input. alice; } March 1, 2005 10 th Estonian Winter School in Computer Science 20

SFDL properties Conventional syntax (C/Pascal-like) • Type system – Boolean, integer, enumerated • Program structure • Declarations: global constants, types – Sequence of functions (no nesting [C], no recursion) – Function name is its return value [Pascal] – • Conditional execution and loops – • if-then, if-then-else statements, For-loop (loop boundaries should be known at compile time) Assignments and expressions – constants, variables, array entries, structure items, function calls, operators (+, -, logical, comparison), parenthesis March 1, 2005 10 th Estonian Winter School in Computer Science 21

SHDL example 0 input //output$input. bob$0 1 input //output$input. bob$1 2 input //output$input. bob$2 3 input //output$input. bob$3 4 input //output$input. alice$0 5 input //output$input. alice$1 6 input //output$input. alice$2 7 input //output$input. alice$3 8 gate arity 2 table [ 1 0 0 0 ] inputs [ 4 5 ] 9 gate arity 2 table [ 0 1 1 0 ] inputs [ 4 5 ] March 1, 2005 10 th Estonian Winter School in Computer Science 22

kth-ranked element (e. g. median) • Inputs: – – • Output: – • x SA SB s. t. x has k-1 elements smaller than it. The rank k – – • Alice: SA Bob: SB Large sets of unique items ( D). Could depend on the size of input datasets. Median: k = (|SA| + |SB|) / 2 Motivation: Basic statistical analysis of distributed data. E. g. histogram of salaries in CS departments • The Problem: Generic constructions using circuits [Yao …] yield an overhead which is at least linear in k. – – March 1, 2005 10 th Estonian Winter School in Computer Science 23

An (insecure) two-party median protocol SA LA m. A RA m. A < m. B SB LB m. B RB LA lies below the median, RB lies above the median. New median is same as original median. Recursion Need log n rounds (assume each set contains n=2 i items) March 1, 2005 10 th Estonian Winter School in Computer Science 24

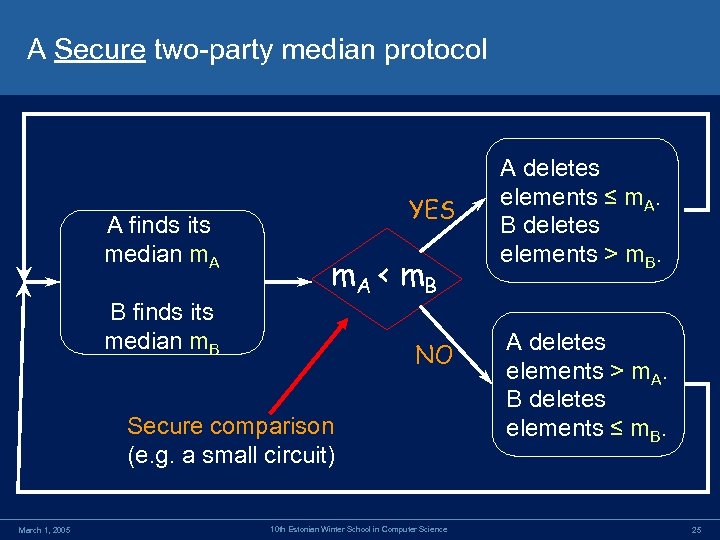A Secure two-party median protocol A finds its median m. A B finds its median m. B YES m. A < m. B NO Secure comparison (e. g. a small circuit) March 1, 2005 10 th Estonian Winter School in Computer Science A deletes elements ≤ m. A. B deletes elements > m. B. A deletes elements > m. A. B deletes elements ≤ m. B. 25

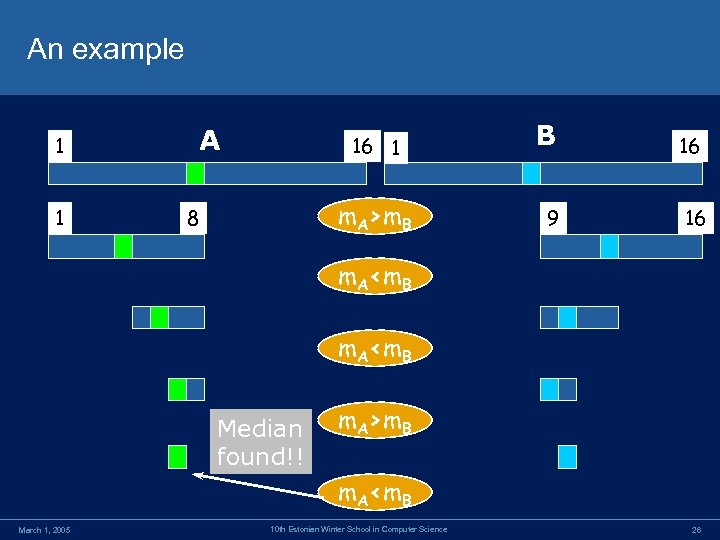An example 1 1 A 16 1 m. A>m. B 8 B 16 9 16 m. Am. B m. A

Proof of security median B A m. A>m. B m. A

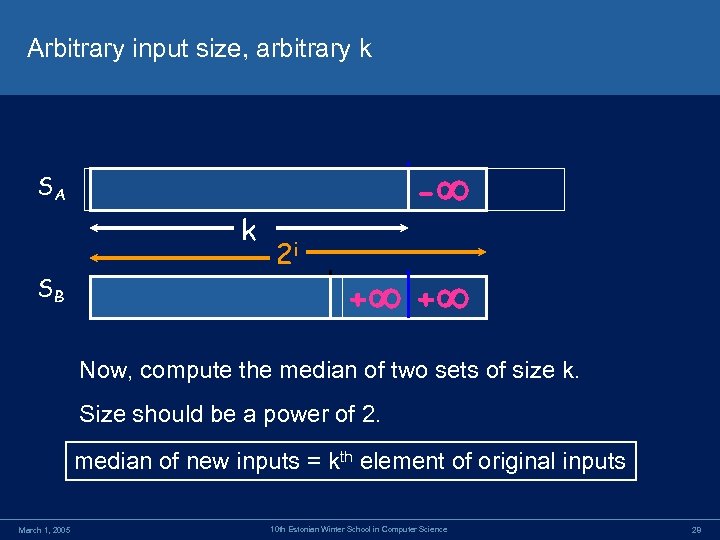Arbitrary input size, arbitrary k - SA k SB 2 i + + Now, compute the median of two sets of size k. Size should be a power of 2. median of new inputs = kth element of original inputs March 1, 2005 10 th Estonian Winter School in Computer Science 28

Hiding size of inputs Can search for kth element without revealing size of input sets. • However, k=n/2 (median) reveals input size. • Solution: Let S=2 i be a bound on input size. • |SA| |SB| March 1, 2005 + - S + - 10 th Estonian Winter School in Computer Science Median of new datasets is same as median of original datasets. 29

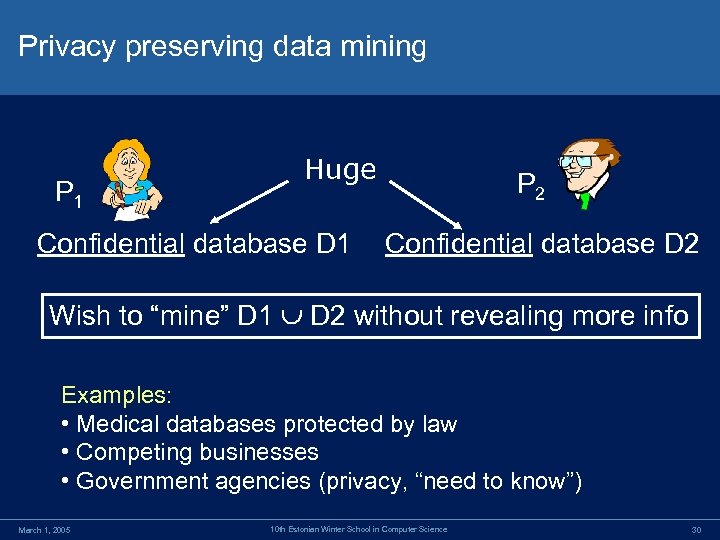Privacy preserving data mining P 1 Huge Confidential database D 1 P 2 Confidential database D 2 Wish to “mine” D 1 D 2 without revealing more info Examples: • Medical databases protected by law • Competing businesses • Government agencies (privacy, “need to know”) March 1, 2005 10 th Estonian Winter School in Computer Science 30

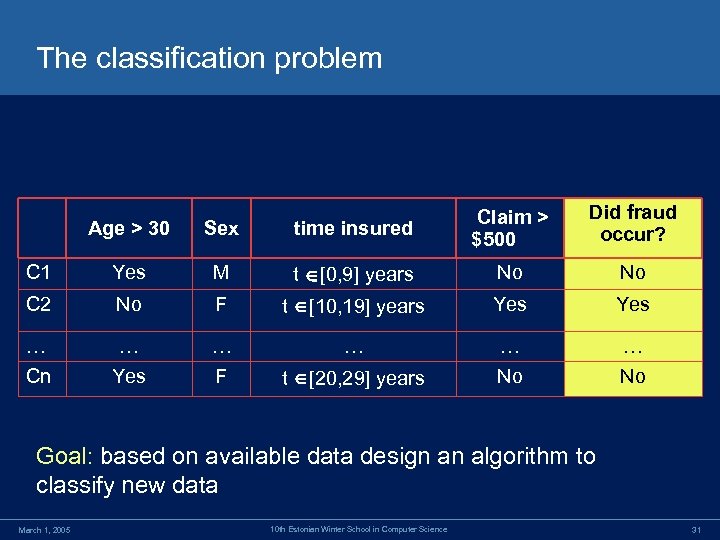The classification problem Did fraud occur? Age > 30 Sex time insured Claim > $500 C 1 Yes M t [0, 9] years No No C 2 No F t [10, 19] years Yes … Cn … Yes … F … … No t [20, 29] years Goal: based on available data design an algorithm to classify new data March 1, 2005 10 th Estonian Winter School in Computer Science 31

Classification using Decision Trees Time insured [0, 9] years ID 3: Choose attribute A that minimizes the conditional entropy of the attribute class > 20 years [10, 19] years Age > 30 Claim > $500 No No No March 1, 2005 Yes No No 10 th Estonian Winter School in Computer Science Yes 32

Privacy Preserving ID 3 • Scenario: The inputs are private information of P 1 and P 2 Main technical problem: Comparing entropies while preserving privacy. (entropy = x logx) • Efficiency: • – – • most computation done independently by parties. The overhead of cryptographic operations depends only on the size of the decision tree (not on the input size). Basic task: compute x log x. x = x 1+x 2 = e. g. , total number of customers with (age > 30) and (fraud = yes) March 1, 2005 10 th Estonian Winter School in Computer Science 33

Privacy Preserving ID 3 • Computing x log x: –x = x 1 + x 2, known to P 1 and P 2 respectively (independently computed from databases). – Might as well compute x lnx, or lnx. – First run a protocol to compute random shares, y 1 + y 2 = ln x • March 1, 2005 ln x is Real. Crypto works over finite fields. Must do numerical analysis. 10 th Estonian Winter School in Computer Science 34

Cryptographic Tools • Secure Function Evaluation (SFE) [Yao] • Oblivious Polynomial Evaluation [NP] Input: Output: A polynomial Q(·) x Q(x) and nothing else nothing Implementation: Two passes, O(degree) (or O( log|F|) ) exponentiations. March 1, 2005 10 th Estonian Winter School in Computer Science 35

Computing random shares of lnx = ln(x 1+x 2) Use Taylor approximation for lnx – x = x 1 + x 2 = 2 n (1+ ) -½ < < ½ – lnx = ln(2 n (1+ )) = ln 2 n + ln(1+ ) ln 2 n + i=1. . k (-1) i-1 i / i = ln 2 n + T( ) • T( ) is a polynomial of degree k. Error is exponentially small in k. • We only know how to work over finite fields • Compute c·lnx, where c compensates for fractions. • Work in F, where |F| sufficiently large. March 1, 2005 10 th Estonian Winter School in Computer Science 36

ln(x 1+x 2) Protocol • Step 1 of the protocol – Find n, – Apply Yao’s protocol to the following small circuit • Input: x 1 and x 2 • Output (random shares): • random a 1 and a 2 s. t. a 1 + a 2 = x-2 n = · 2 n • random b 1 and b 2 s. t. b 1 + b 2 = ln 2 n • Operation: The protocol finds 2 closest to x 1+x 2, computes 2 n = x 1+x 2 - 2 n. –x – March 1, 2005 n = x 1 + x 2 = 2 n + 2 n lnx = ln(2 n (1+ )) = ln 2 n + ln(1+ ) 10 th Estonian Winter School in Computer Science 37

ln(x 1+x 2) Protocol (Cont. ) Step 2 of the protocol – Compute random shares of T( ) (Taylor approx. ) – P 1 chooses a random w 1 F and defines a polynomial Q(x), s. t. w 1 +Q(a 2) = T( ) (recall a 1 + a 2 = · 2 n) – Namely, Q(x) = T( (a 1+x)/2 n ) – w 1. – Run an oblivious poly evaluation in which P 2 computes w 2 = Q(a 2) = T( ) – w 1. – Now the parties have random w 1 and w 2 s. t. – w 1 + w 2 = T( ) ln(1+ ) – (b 1 + w 1) + (b 2 + w 2) ln 2 n + ln(1+ ) = ln x March 1, 2005 10 th Estonian Winter School in Computer Science 38

The rest of the work. . • • • The parties compute shares of lnx Then they compute shares of xlnx Each party computes a share of the entropy by summing shares of x lnx (H(X) = x lnx ) A small circuit finds the attribute giving the minimal conditional entropy The attribute is assigned to the node The databases are divided according to the value of this attribute March 1, 2005 10 th Estonian Winter School in Computer Science 40

Efficiency • lnx protocol: – secure computation of a small circuit – one oblivious polynomial evaluation • ID 3 for a database with: – – 1, 000 transactions 15 attributes 10 values per attribute 4 class values – Communication per node takes seconds (T 1) – Computation per node takes minutes (P 3) March 1, 2005 10 th Estonian Winter School in Computer Science 41

Contributions Cryptographic protocols where the bulk of the operations is done independently. • Data mining • Rigorous model for secure data-mining. – Efficient, secure protocol for specific problems (median, ID 3). – • Cryptography Sub-linear complexity - secure computation for large data sets. – Efficient protocols for complex known algorithms. – Secure computation of logarithms (real function - numerical analysis). – • Drawbacks: Privacy preserving solutions are less efficient – It’s hard to find efficient private solutions for all interesting functions – Security against malicious parties – March 1, 2005 10 th Estonian Winter School in Computer Science 42

References • Lecture notes and overview papers: B. Pinkas, Cryptographic Techniques for Privacy-Preserving Data Mining, SIGKDD Explorations, January 2003. http: //www. pinkas. net/PAPERS/sigkdd. pdf – R. Cramer: Introduction to Secure Computation, 2000. http: //homepages. cwi. nl/~cramer/papers/CRAMER_revised. ps – Ivan Damgård, Theory and practice of multiparty computation, 8 th EWSCS, http: //www. cs. ioc. ee/yik/schools/win 2003/damgard. php – • Research papers: G. Aggarwal, N. Mishra and B. Pinkas, Secure Computation of the K'th-ranked Element, Eurocrypt '2004. http: //www. pinkas. net/PAPERS/ANP 04. pdf – Y. Lindell and B. Pinkas, Privacy Preserving Data Mining, Journal of Cryptology, Vol. 15 – No. 3, 2002. http: //www. pinkas. net/PAPERS/id 3 final. pdf – March 1, 2005 10 th Estonian Winter School in Computer Science 43