Принятие решения в многокритериальных задачах Основными этапами

Принятие решения в многокритериальных задачах

Основными этапами решения любой задачи в теории принятия решений являются: построение модели; ¡ выбор критерия оптимальности; ¡ нахождение оптимального решения. Для построения оценочной функции необходим некоторый измеримый критерий эффективности исходов. Однако в большинстве практических задачах принятия решения исходы оцениваются, как правило, не по одному, а по нескольким критериям. Критерий – это показатель качества. ¡

¡ Если исходы оцениваются по m критериям, где m > 1, то такая задача принятия решений называется многокритериальной. ¡ Основная сложность логического анализа многокритериальных задач состоит в том, что в них, в отличие от «обычных» (однокритериальных) задач появляется эффект несравнимости исходов.

¡ Несравнимость исходов является формой неопределённости, которая, в отличие от стратегической неопределённости, вызванной воздействием среды на объект управления, связана со стремлением лица принимающего решение «достичь противоречивых целей» и может быть названа ценностной неопределённостью. ¡ Выбор между несравнимыми исходами является сложной концептуальной проблемой и составляет основное содержание многокритериальной оптимизации.

Математическая модель задачи (D; f 1, …, fm), D – некоторое множество (множество допустимых исходов), fj – числовая функция, заданная на множестве D. При этом fj (a), оценка исхода a, принадлежащего D по j-му критерию (j=1, …, m). Такая модель соответствует задаче принятия решения в условиях определённости, в которой множество альтернатив отождествляется с множеством допустимых исходов, а оценочная структура задаётся вектором (f 1, …, fm).

Критерий называется позитивным, если большему значению критерия соответствует лучший исход. И негативным в противном случае. Пусть Yj- множество значений функции Тогда множество Y = состоящее из всевозможных упорядоченных наборов оценок по критериям (j=1, …, m) , называется множеством векторных оценок. Любой элемент y Y представляет собой вектор y=(y 1, …, ym), где yj Yj. Для всякого исхода a D набор его оценок по всем критериям, т. е. набор (f 1(a), … , fm(a)) есть векторная оценка исхода a.

Отношение доминирования по Парето Определение. Говорят, что векторная оценка y=(y 1, …, ym) доминирует по Парето векторную оценку = ( , …, ) (записывается в виде: ), если для всех j выполняется неравенство причём по крайней мере для одного индекса j неравенство должно быть строгим.

Отношение доминирования по Парето Определение. Пусть Q - некоторое множество векторных оценок. Векторная оценка y* Q называется Паретооптимальной в Q , если она является максимальным элементом множества Q относительно Паретодоминирования (т. е. если в множестве Q не существует такой векторной оценки y, которая доминирует по Парето векторную оценку y*).

Отношение доминирования по Парето Определение. Говорят, что исход доминирует по Парето исход (записывается в виде ), если векторная оценка исхода доминирует по Парето векторную оценку исхода . Определение. Исход называется Парето-оптимальным исходом во множестве D, если он не доминируется по Парето никаким другим исходом из множества D (т. е. если векторная оценка исхода a* является Парето-оптимальной во множестве векторных оценок

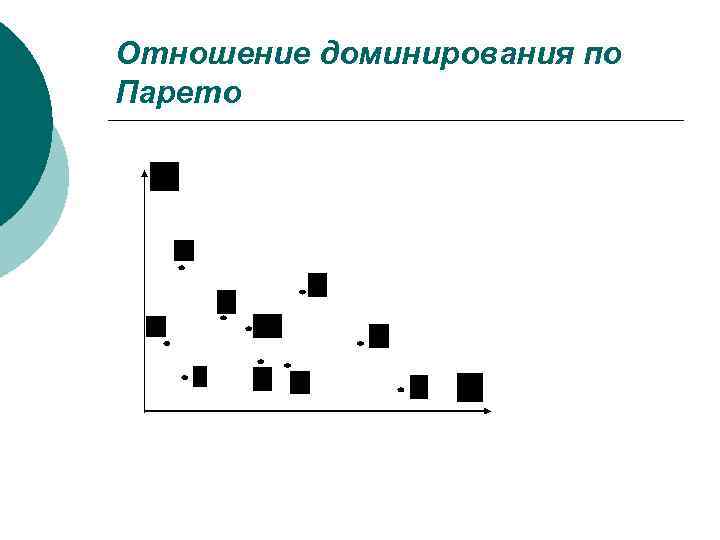Отношение доминирования по Парето

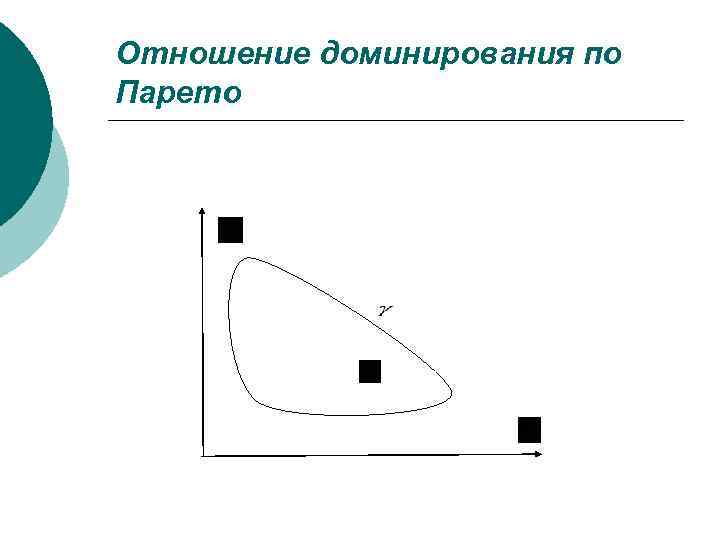Отношение доминирования по Парето

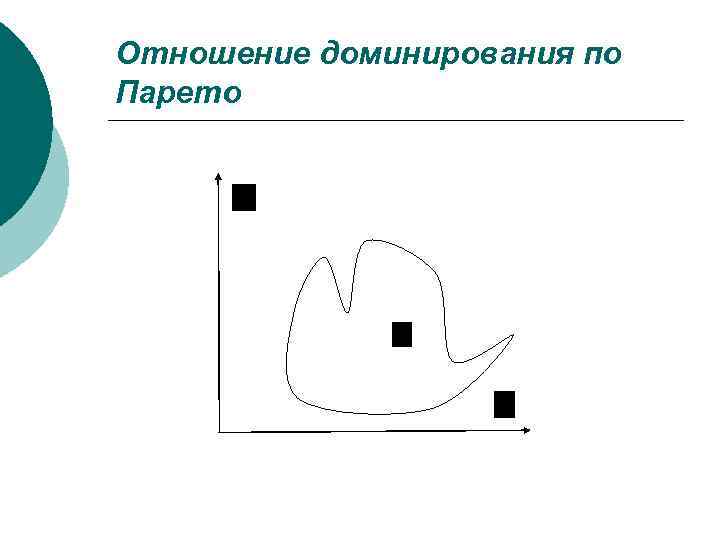Отношение доминирования по Парето

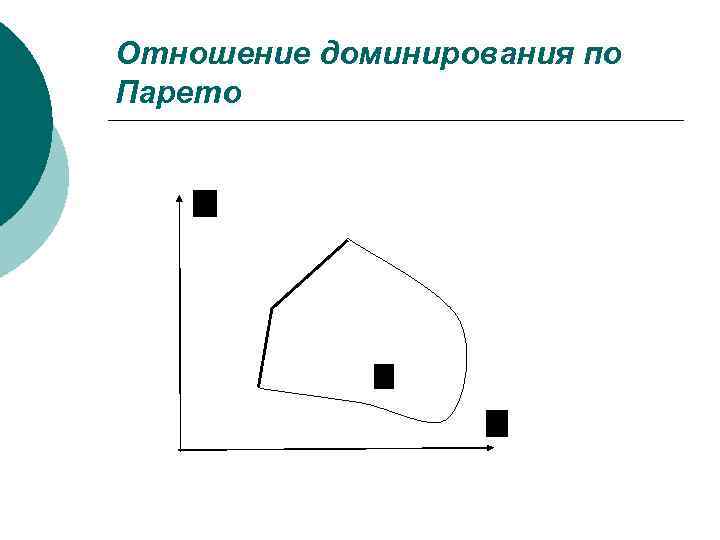Отношение доминирования по Парето

Парето-оптимальность исхода – необходимое условие оптимальности (но не достаточное) ¡ ¡ I подход. Для заданной многокритериальной ЗПР находится множество её Парето-оптимальных исходов, а выбор конкретного оптимального исхода из множества Парето-оптимальных предоставляется ЛПР II подход. Производится сужение множества Паретооптимальных исходов с помощью некоторых формализованных процедур, что облегчает окончательный выбор исхода для ЛПР. Но такое сужение может быть произведено только при наличии дополнительной информации о критериях или о свойствах оптимального решения.

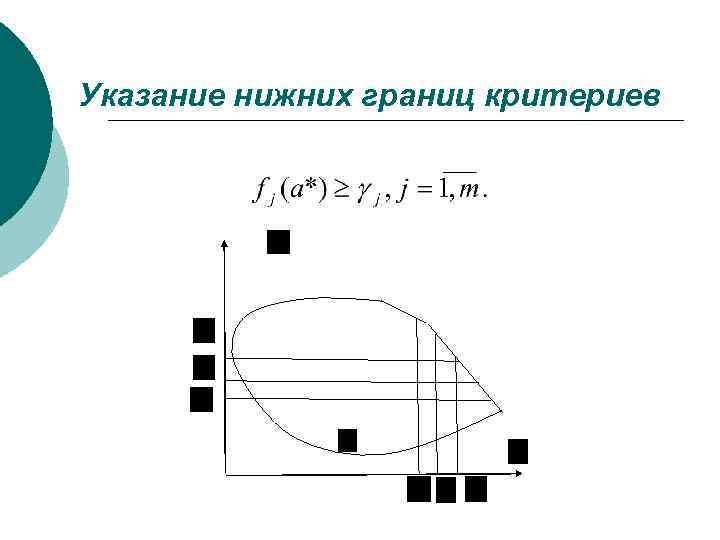Указание нижних границ критериев

Субоптимизация Выделяем один из критериев, а по всем остальным критериям назначаем нижние границы. Оптимальным при этом считается исход, максимизирующий выделенный критерий на множестве исходов, оценки которых по остальным критериям не ниже назначенных. С помощью метода субоптимизации задача многокритериальной оптимизации превращается в задачу «обычной» (скалярной) оптимизации на суженном допустимом множестве.

Лексикографическая оптимизация основана на упорядочении критериев по их относительной важности. Отбирают исходы, которые имеют максимальную оценку по важнейшему критерию. Если такой исход единственный, то его и считают оптимальным. Если же таких исходов несколько, то среди них отбирают те, которые имеют максимальную оценку по следующему (за важнейшим критерию) и т. д. В результате такой процедуры всегда остаётся (по крайней мере, в случае конечного множества исходов) единственный исход – он и будет оптимальным.

Задача. Выбор места работы. Предположим, что Вам предстоит выбрать место работы из девяти вариантов, представленных в таблице. В качестве основных критериев взята: зарплата З, длительность отпуска Д, время поездки на работу В. Так критерий В имеет характер потерь, оценки по этому критерию берутся со знаком «минус» . Какой вариант является оптимальным?

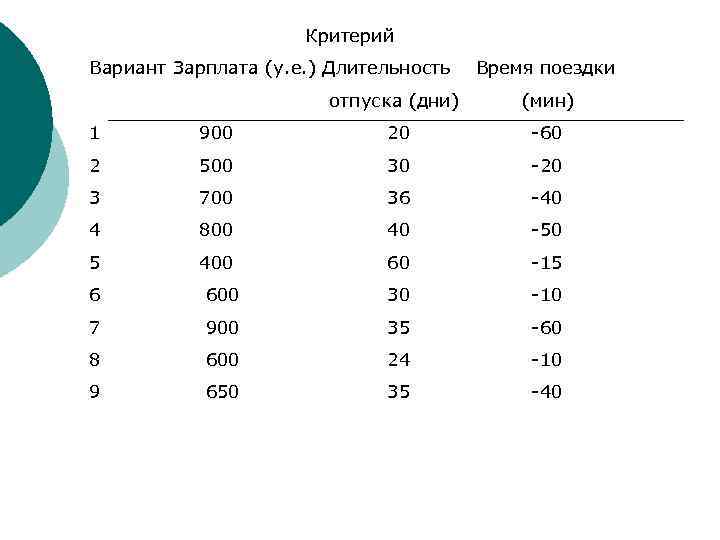Критерий Вариант Зарплата (у. е. ) Длительность Время поездки отпуска (дни) (мин) 1 900 20 -60 2 500 30 -20 3 700 36 -40 4 800 40 -50 5 400 60 -15 6 600 30 -10 7 900 35 -60 8 600 24 -10 9 650 35 -40

Парето-оптимальное множество {3, 4, 5, 6, 7}. а) Указание нижних границ критериев. зарплата – не менее 600; длительность отпуска – не менее 30 дней; время поездки – не более 40 мин. Варианты, удовлетворяющие этим дополнительным ограничениям: {3, 6, 9}; из них оптимальными по Парето является варианты 3 и 6. Остаётся сделать окончательный выбор между вариантами 3 и 6.

б) Субоптимизация. Пусть в качестве выделенного критерия выступает критерий зарплата; ограничения: длительность отпуска – не менее 30 дней, время поездки – не более 40 мин. Остаются варианты: {2, 3, 5, 6, 9}. Из них максимальную зарплату имеет вариант 3. Этот вариант и будет оптимальным. в) Лексикографическая оптимизация. Упорядочим критерии по относительной важности, например, следующим образом: ЗВД Максимальное значение по критерию З имеют варианты 1 и 7. Далее сравниваем эти варианты по второму по важности критерию В. Так как время поездки для этих вариантов одинаково, переходим к третьему критерию Д; по критерию длительность отпуска лучшим является вариант 7, который и является здесь оптимальным. При упорядочении ВДЗ оптимальным будет вариант 6, а при упорядочении ДЗВ – оптимальным становится вариант 5. Замечание 1. У лексикографической оптимизации есть недостаток – фактический учёт одного (важнейшего) критерия. Например, в последнем случае в качестве оптимального выступает вариант 5, который имеет самую низкую оценку по критерию зарплат.

Построение обобщённого критерия Под построением обобщённого критерия в многокритериальной ЗПР понимается процедура, которая «синтезирует» набор оценок по заданным критериям в единую численную оценку, выражающую итоговую полезность этого набора оценок для принимающего решение. Если обобщённый критерий построен, то для каждого допустимого исхода a D может быть найдена численная оценка его полезности.

¡ ¡ Задание обобщённого критерия сводит задачу многокритериальной оптимизации к задаче однокритериальной оптимизации с целевой функцией f. Наиболее распространённым обобщённым критерием является «взвешенная сумма частных критериев» , которая превращает векторную оценку в скалярную оценку Числа в этом случае называют весовыми коэффициентами.

Правило 1. Пусть Q - произвольное множество векторных оценок. Если векторная оценка доставляет максимум функции где >0, то векторная оценка y* является Парето-оптимальной во множестве Q. Правило 2. Пусть Q - выпуклое множество, - Паретооптимальная векторная оценка на множестве Q. Тогда найдутся такие неотрицательные числа , что функция достигает максимума на множестве Q в точке.

Проблема построения обобщенного критерия в многокритериальной ЗПР Зарплата (руб) Длительность отпуска (дни) Время поездки (мин) А 900 20 -60 В 500 30 -40

M 1=900, M 2=30, M 3=60, откуда Так как > то альтернатива В более предпочтительна, чем альтернатива А. Пусть теперь наряду с альтернативами А и В появилась ещё одна альтернатива С, которая характеризуется векторной оценкой (400, 60, -100). В этом случае M 1’=900, M 2’=60, M 3’=100.

¡ ¡ Получаем, что теперь альтернатива А стала более предпочтительной, чем альтернатива В, т. е. порядок предпочтения альтернатив А и В получился в этом случае обратным! Итак, наличие ещё одной альтернативы С меняет предпочтения между альтернативами А и В. Это парадоксальное свойство называется нарушением независимости предпочтений относительно посторонних альтернатив. При этом следует заметить, что дополнительная альтернатива С здесь не конкурирует ни с А, ни с В, так как А и В предпочтительнее, чем С.

Принципиальная сложность построения обобщенного критерия заключена в том, что приходится «соотносить» друг с другом критерии, характеризующие объект с разных сторон; эти критерии имеют часто совершенно различную природу, в силу чего оценки по ним даются в разных шкалах. Построение итоговой ( «интегральной» ) оценки невозможно без соизмерения критериев между собой, что требует большой дополнительной информации об относительной важности этих критериев для принимающего решение.