Принципы симметрии Выполнила студентка 1 курса Сметанникова Александра

Принципы симметрии Выполнила студентка 1 курса Сметанникова Александра Преподаватель доктор медицинских наук профессор П. К. Котенко

Содержание: • • • • Симметрия в математике, физике Центральная симметрия Симметрия вращения Осевая симметрия Зеркальная симметрия Симметрия в живой природе Симметрия растений Симметрия животных Асимметрия живого Человек существо симметричное Симметрия в неживой природе Симметрия кристаллов Заключение

Симметрия в математике, физике • По справедливому замечанию Германа Вейля (известный математик прошлого столетия), у истоков симметрии лежит математика. Замечательные слова, сказанные им: «Симметрия… есть идея, с помощью которой человек веками пытался объяснить и создать порядок, красоту и совершенство» . • Но вместе с тем симметрия воспринимается на ми как элемент красоты вообще и красоты природы в частности. Математики вкладывают в понятие симметрия точный математический смысл, рассматривают специальные виды симметрии. И в результате симметрия становится мощным средством математических исследований, помогает решать трудные задачи.

• • • Итак, геометрический объект или физическое явление считаются симметричными, если с ними можно сделать что то такое, после чего они останутся неизменными. И если говорить о геометрических объектах, то симметрию можно будет называть геометрической, если о физических явлениях, то – физическая симметрия. Например, пятиконечная звезда, будучи повёрнута на 72° (360°: 5), займёт первоначальное положение, а ваш будильник одинаково звенит в любом углу комнаты. Благодаря симметрии все физические приборы (в том числе и будильник) одинаково работают в разных точках пространства, если, конечно, не изменяются окружающие физические условия. Легко вообразить, какая бы царила на Земле неразбериха, если бы эта симметрия была нарушена: вещи бы были непонятной формы, зеркало бы показывало наше отражение задом, а не передом, а мы бы с вами просто не смогли бы ходить, видели одним глазом и ели бы одной рукой. Таким образом, общим для всех них (геометрических объектов или физических явлений) принципом симметрии пронизаны многообразные физические и биологические законы гравитации, электричества и магнетизма, ядерных взаимодействий, наследственности, начиная от текстильного производства, кончая тонкими вопросами строения вещества.

Центральная симметрия • Понятие центральной симметрии следующее: «Фигура называется симметрич ной относительно точки , если О для каж дой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре. Точка О называется центром симметрии фигуры» . Поэтому говорят, что фи гура обладает центральной симметрией.

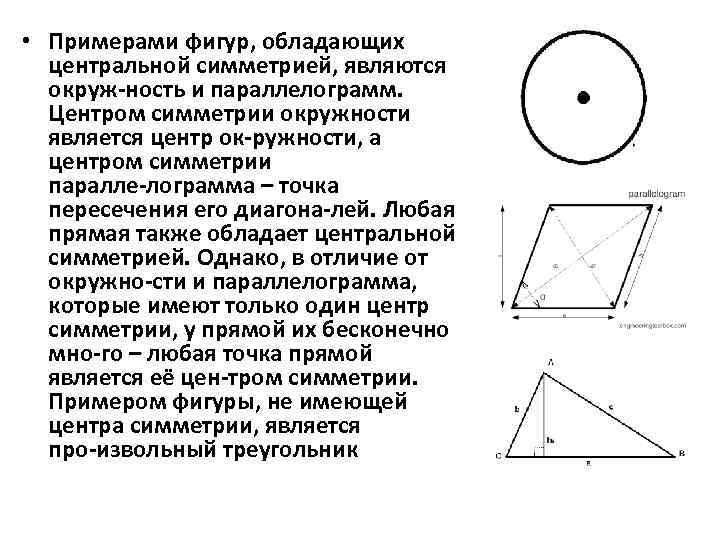• Примерами фигур, обладающих центральной симметрией, являются окруж ность и параллелограмм. Центром симметрии окружности является центр ок ружности, а центром симметрии паралле лограмма – точка пересечения его диагона лей. Любая прямая также обладает центральной симметрией. Однако, в отличие от окружно сти и параллелограмма, которые имеют только один центр симметрии, у прямой их бесконечно мно го – любая точка прямой является её цен тром симметрии. Примером фигуры, не имеющей центра симметрии, является про извольный треугольник

Симметрия вращения • • Тело (или фигура) обладает симметрией вращения, если при повороте на угол 360º/n, где n целое число, около некоторой прямой АВ (ось симметрии) оно полностью совмещается со своим исходным положением. Если число n равно 2, 3, 4 и т. д. , то ось симметрии называется осью второго, третьего и т. д. порядка. Например, если мы разрежем круг на три части с центральными углами по 120º, наложим эти секторы друг на друга (не переворачивая их другой стороной) и прорежем на них фигуру а произвольной формы, то, сложив снова части так, как они лежали, получим фигуру (круг с дырочками), обладающую осью симметрии 3 его порядка. Эта ось перпендикулярна к плоскости чертежа. Поворотом на 120º фигура полностью совмещается со своим исходным положением

• Радиальная симметрия – форма симметрии, сохраняющаяся при вращении объекта вокруг определённой точки или прямой. Часто эта точка совпадает с центром тяжести объекта, то есть той точкой, в которой пересекается бесконечное количество осей симметрии. Подобными объектами могут быть круг, шар, цилиндр или конус. • Шар обладает и центральной, и зеркальной, и осевой симметрией. • Круглый конус имеет осевую симметрию (любого по рядка); ось симметрии — ось конуса. • Правильная пятиугольная призма имеет плоскость симметрии, идущую параллельно основаниям на равном от них расстоянии, и ось симметрии пятого порядка, со впадающую с осью призмы.

Осевая симметрия • Понятие осевой симметрии представлено следующим образом: «Фигура называется симметрич ной относительно прямой , а если для каж дой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре. Прямая a называется осью симметрии фигуры» . Тогда говорят, что фи гура обладает осевой симметрией.

• Приведу примеры фигур, обла дающих осевой симметрией. У неразвернутого угла одна ось симметрии — прямая, на которой расположена биссект риса угла. Равнобедренный (но не равносто ронний) треугольник имеет также одну ось симметрии, а равносторонний треуголь ник— три оси симметрии. Прямоугольник и ромб, не являющиеся квадратами, имеют по две оси симметрии, а квадрат— четыре оси симметрии. У окружности их бесконеч но много — любая прямая, проходящая че рез её центр, является осью симметрии. • Имеются фигуры, у которых нет ни одной оси симметрии. К таким фигурам относятся параллелограмм, отлич ный от прямоугольника, разносторонний треугольник Равнобедренный (но не равносторонний) тре угольник имеет также одну ось симметрии, а равносторонний - три оси.

Зеркальная симметрия • Зеркальная симметрия хорошо знакома каждому человеку из повседневного наблюдения. Как показывает само название, зеркальная симметрия связывает любой предмет и его отражение в плоском зеркале. Говорят, что одна фигура (или тело) зеркально симметрично другой, если вместе они образуют зеркально симметричную фигуру (или тело)

• Важно отметить, что два симметричных другу тела не могут быть вложены или наложены друг на друга. Так перчатку правой руки нельзя надеть на левую руку. • Симметрично зеркальные фигуры при всём своём сходстве существенно отличаются друг от друга. Чтобы убедиться в этом, достаточно поднести лист бумаги к зеркалу и попытаться прочесть несколько слов, напечатанных на ней, буквы и слова просто напросто будут перевёрнуты справа налево. По этой причине симметричные предметы нельзя называть равными, поэтому их называют зеркально равными.

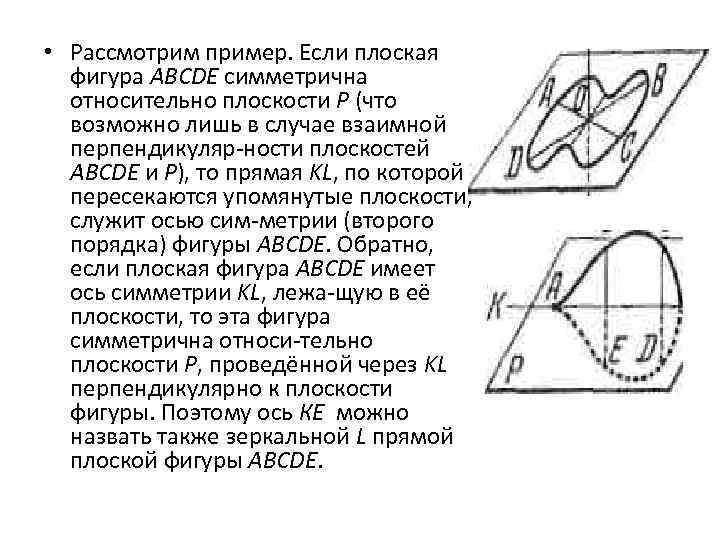• Рассмотрим пример. Если плоская фигура ABCDE симметрична относительно плоскости Р (что возможно лишь в случае взаимной перпендикуляр ности плоскостей ABCDE и Р), то прямая KL, по которой пересекаются упомянутые плоскости, служит осью сим метрии (второго порядка) фигуры ABCDE. Обратно, если плоская фигура ABCDE имеет ось симметрии KL, лежа щую в её плоскости, то эта фигура симметрична относи тельно плоскости Р, проведённой через KL перпендикулярно к плоскости фигуры. Поэтому ось КЕ можно назвать также зеркальной L прямой плоской фигуры ABCDE.

Симметрия в живой природе • Среди бесконечного разнообразия форм живой и неживой природы в изобилии встречаются такие совершенные образцы, чей вид неизменно привлекает наше внимание и ласкает наш взгляд. К числу таких образцов относятся некоторые кристаллы и микробы, многие животные и растения. Мы постоянно любуемся прелестью каждого отдельного цветка, мотылька или раковины и всегда пытаемся проникнуть в тайну их красоты. Нас удивляет и архитектура пчелиных сот, и расположение семян на шапке подсолнечника, и винтообразное расположение листьев на стебле растения

• У биологических объектов встречаются следующие типы симметрии: • а) сферическая симметрия — симметричность относительно вращений в трёхмерном пространстве на произвольные углы; • б) симметрия n го порядка — симметричность относительно поворотов на угол 360°/n вокруг какой либо оси; • в) аксиальная симметрия (радиальная ) — симметричность относительно поворотов на произвольный угол вокруг какой либо оси; • г) двусторонняя (билатеральная) симметрия (от би. . . и лат. lateralis — боковой) — симметричность относительно зеркального отражения; выражается в том, что тело живых организмов делится срединной плоскостью на правую и левую половины, представляющие как бы зеркальное отражение одна другой. ; • д) трансляционная симметрия — симметричность относительно сдвигов пространства в каком либо направлении на некоторое расстояние; • е) триаксиальная асимметрия — отсутствие симметрии по всем трём пространственным осям.

Симметрия растений Изображения на плоскости мно гих предметов окружающего нас мира име ют ось симметрии или центр симметрии. Многие листья деревьев и лепестки цветов симметричны относительно среднего стебля. Среди цветов наблюдаются поворотные симметрии разных порядков. Многие цветы обладают характерным свойством: цветок можно повернуть так, что каждый лепесток займёт положение соседнего, цветок же совместится с самим собой. Такой цветок обладает осью симметрии. Минимальный угол, на который нужно повернуть цветок вокруг оси симметрии, чтобы он совместился с самим собой, называется элементарным углом поворота оси

Симметрия животных • Внимательное наблюдение обнаруживает, что основу красоты многих форм, созданных природой, составляет симметрия, точнее, все её виды – от простейших до самых сложных. Симметрия в строение животных – почти общее явление, хотя почти всегда встречаются исключения из общего правила.

• Под симметрией у животных понимают соответствие в размерах, форме и очертаниях, а также относительное расположение частей тела, находящихся на противоположных сторонах разделяющей линии. Строение тела многих многоклеточных организмов отражает определённые формы симметрии, такие как радиальную (лучевая) или билатеральную (двусторонняя), которые являются основными типами симметрии. Кстати, склонность к регенерации (восстановление) зависит от типа симметрии животного

Асимметрия живого • Понятия симметрии и асимметрии альтернативны: чем более симметричен организм, тем менее он асимметричен и наоборот. Небольшое количество организмов полностью асимметричны. При этом следует различать отсутствие формы (например, у амёбы) от отсутствия симметрии. В природе и биологии симметрия не абсолютна и всегда содержит некоторую степень асимметрии. Например, симметричные листья растений при сложении пополам в точности не совпадают.

• Симметрия в строении животных – почти общее явление, хотя почти всегда встречаются исключения из общего правила, выражающиеся в асимметричном положении той или другой части или того или другого органа. Например, наиболее резким примером асимметричной конфигурации могут служить камбалы и особенно смещение их глаз. Асимметрия (греч. α – «без» и «симметрия» ) – отсутствие симметрии.

Человек существо симметричное • Не станем пока разбираться, существует ли на самом деле абсолютно симметричный человек. У каждого, разумеется, обнаружится родинка, прядь волос или какая нибудь другая деталь, нарушающая внешнюю симметрию. Левый глаз никогда не бывает в точности таким, как правый, да и уголки рта находятся на разной высоте, во всяком случае, у большинства людей. И всё же это лишь мелкие несоответствия. • Никто не усомнится, что внешне человек построен симметрично: левой руке всегда соответствует правая и обе руки совершенно одинаковы! НО! Здесь стоит остановиться. Если бы наши руки и в самом деле были совершенно одинаковы, мы могли бы в любой момент поменять их. Было бы возможно, скажем, путем трансплантации пересадить левую ладонь на правую руку, или, проще, левая перчатка подходила бы тогда к правой руке, но на самом деле это не так. Каждому известно, что сходство между нашими руками, ушами, глазами и другими частями тела такое же, как между предметом и его отражением в зеркале. Многие художники обращали пристальное внимание на симметрию и пропорции человеческого тела, во всяком случае, до тех пор, пока ими руководило желание в своих произведениях как можно точнее следовать природе.

• Известны каноны пропорций, составленные Альбрехтом Дюрером и Леонардо да Винчи. Согласно этим канонам, человеческое тело не только симметрично, но и пропорционально. Леонардо открыл, что тело вписывается в круг и в квадрат. Дюрер занимался поисками единой меры, которая находилась бы в определенном соотношении с длиной туловища или ноги (такой мерой он считал длину руки до локтя).

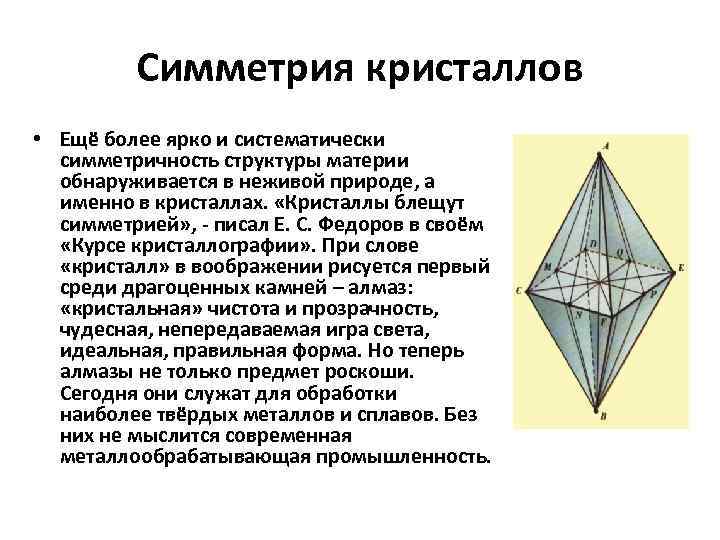Симметрия кристаллов • Ещё более ярко и систематически симметричность структуры материи обнаруживается в неживой природе, а именно в кристаллах. «Кристаллы блещут симметрией» , писал Е. С. Федоров в своём «Курсе кристаллографии» . При слове «кристалл» в воображении рисуется первый среди драгоценных камней – алмаз: «кристальная» чистота и прозрачность, чудесная, непередаваемая игра света, идеальная, правильная форма. Но теперь алмазы не только предмет роскоши. Сегодня они служат для обработки наиболее твёрдых металлов и сплавов. Без них не мыслится современная металлообрабатывающая промышленность.

• Оказывается, не только алмаз кристалл. Обычный сахар и поваренная соль, лёд и песок состоят из множества кристалликов. Больше того, основная масса горных пород, образующих земную кору, состоит из кристаллов. Даже обыкновенная глина представляет собой нагромождение мельчайших кристалликов. Словом, большинство строительных материалов – металлы, камень, песок, глина – кристаллические вещества. Можно сказать, что мы живём в домах, построенных из кристаллов. Неудивительно, что кристаллы являются предметом тщательного изучения. Кристаллы – это твердые тела, имеющие естественную форму многогранника. Для каждого данного вещества существует своя, присущая только ему одному, идеальная форма его кристалла. Эта форма обладает свойством симметрии, т. е. свойством кристаллов совмещаться с собой в различных положениях путём поворотов, отражений, параллельных переносов.

Заключение • И в заключении хочу сказать о том, что быть прекрасным значит быть симметричным и соразмерным. • Доктор Марио Ливио (Mario Livio) из института Space Telescope Science Institute в Балтиморе сделал предположение, что стремление человека к упорядоченным структурам и симметричным объектам не позволяет нам видеть окружающий мир таким, какой он есть в действительности, и законы природы на самом деле могут и не подчиняться законам симметрии, сообщает Live Science. • Симметрия в науке, искусстве и природе давно стала предметом изучения. Известный математик начала ХХ века Джордж Дэвид Беркофф (George David Birkhoff ) из Гарвардского университета вывел математическую формулу для измерения красоты и притягательности произведений искусства. В формуле присутствуют два абстрактных понятия — сложность и упорядоченность (или симметрия). Согласно теории Беркоффа, сложный объект более привлекателен с эстетической точки зрения, если он менее симметричен, и наоборот, симметричный объект должен быть простым по строению. Но метод измерения степени сложности и симметричности объекта, предложенный Беркоффом, показался ученым слишком субъективными, и формула вскоре была забыта.