Принципы решения биматричных игр. Биматричные игры n*m. Биматричные игры 2*2 Выполнил: Подкорытов А. В.
Определение: Биматричная игра – это конечная игра двух игроков с ненулевой суммой, в которой выигрыши каждого игрока задаются матрицами отдельно для соответствующего игрока (в каждой матрице строка соответствует стратегии игрока 1, столбец – стратегии игрока 2, на пересечении строки и столбца в первой матрице находится выигрыш игрока 1, во второй матрице – выигрыш игрока 2).
Виды Биматричных игр: Бескоалиционный Коалиционные Бесконечные Конечные
Биматричные игры n*m.
Матрицы выигрышей:
Вероятность выбора стратегий:
Формулы для случая M*N. Средние выигрыши.
Формулы для случая M*N. Ситуация равновесия:
Формулы для случая M*N. Условия равновесия:
Биматричные игры 2*2.
Матрицы выигрышей:
Смешанные стратегии:
Средние выигрыши:
Условия для ситуации равновесия:
Упростим ситуацию равновесия для первого игрока:
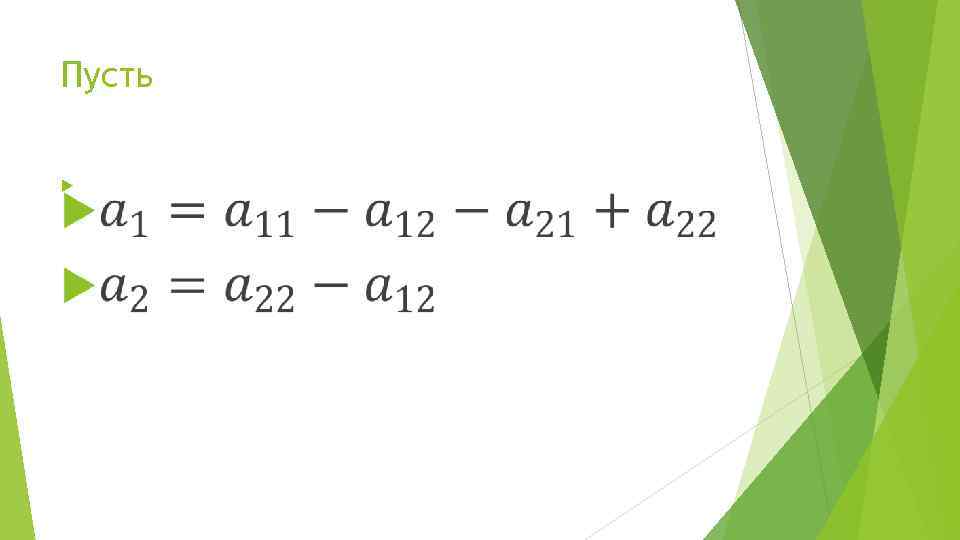
Пусть
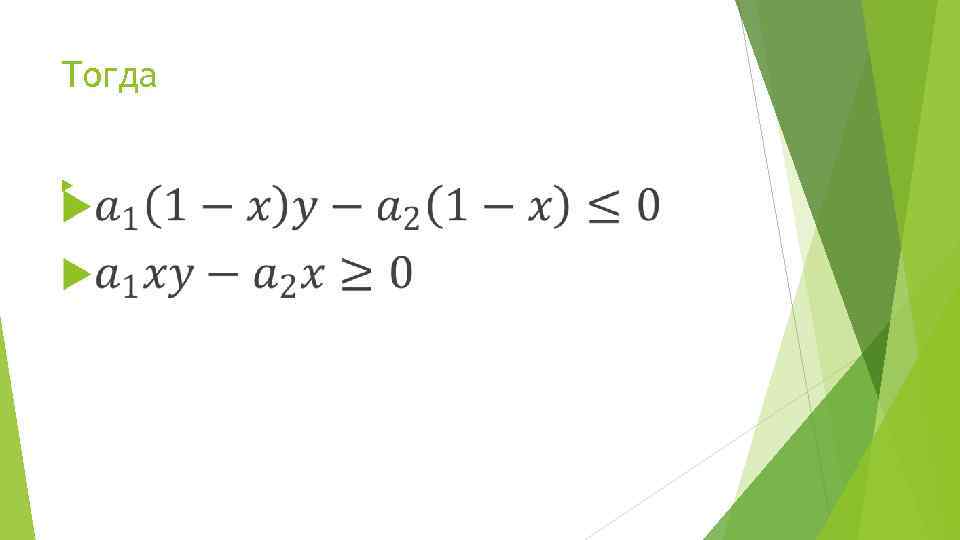
Тогда
Итак,
Найдем х:
Для второго игрока исследования аналогичны.
Множество L решения для второго игрока состоит из:
Результаты следующие:
Итог решения игры 2 х2 Решение игры является пересечение множеств K и L, то есть те значения х и у, которые являются общими для множеств K и L. Средние выигрыши при этом определяются по формуле
Пример решения биматричной игры 2*2.
Условия задачи: Министерство желает построить один из двух объектов на территории города. Городские власти могут принять предложение министерства или отказать. Министерствопервый игрок- имеет две стратегии: строит 1 -й объект, строить 2 й объект. Город-второй игрокимеет две стратегии: принять предложение министерства или отказать. Свои действия(стратегии) они применяют независимо друг от друга.
Матрицы выигрышей:
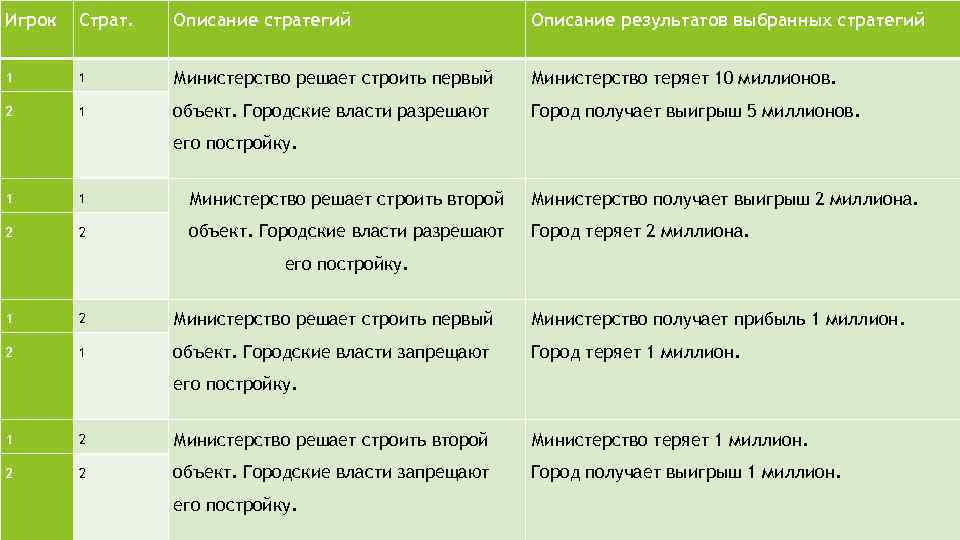
Игрок Страт. Описание стратегий Описание результатов выбранных стратегий 1 1 Министерство решает строить первый Министерство теряет 10 миллионов. 2 1 объект. Городские власти разрешают Город получает выигрыш 5 миллионов. его постройку. 1 1 Министерство решает строить второй Министерство получает выигрыш 2 миллиона. 2 2 объект. Городские власти разрешают Город теряет 2 миллиона. его постройку. 1 2 Министерство решает строить первый Министерство получает прибыль 1 миллион. 2 1 объект. Городские власти запрещают Город теряет 1 миллион. его постройку. 1 2 Министерство решает строить второй Министерство теряет 1 миллион. 2 2 объект. Городские власти запрещают Город получает выигрыш 1 миллион. его постройку.
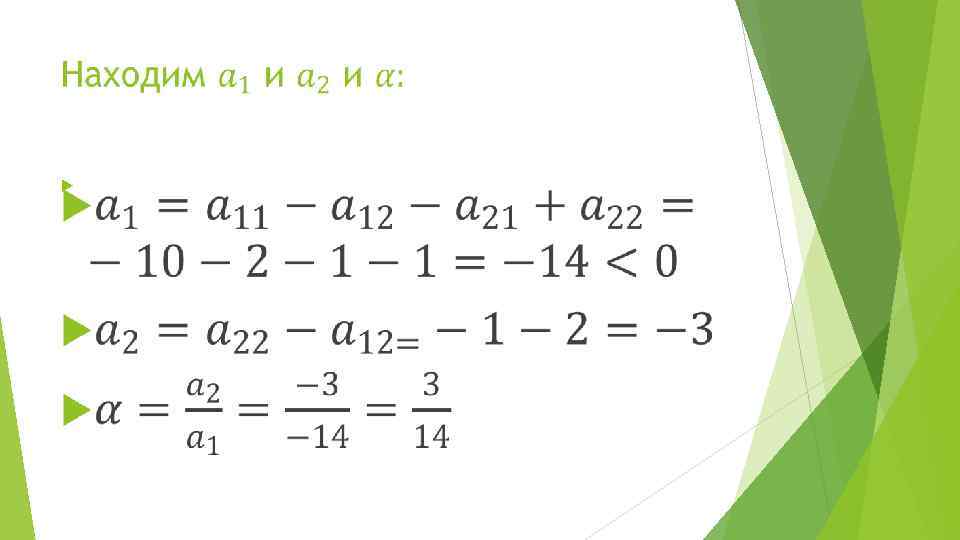
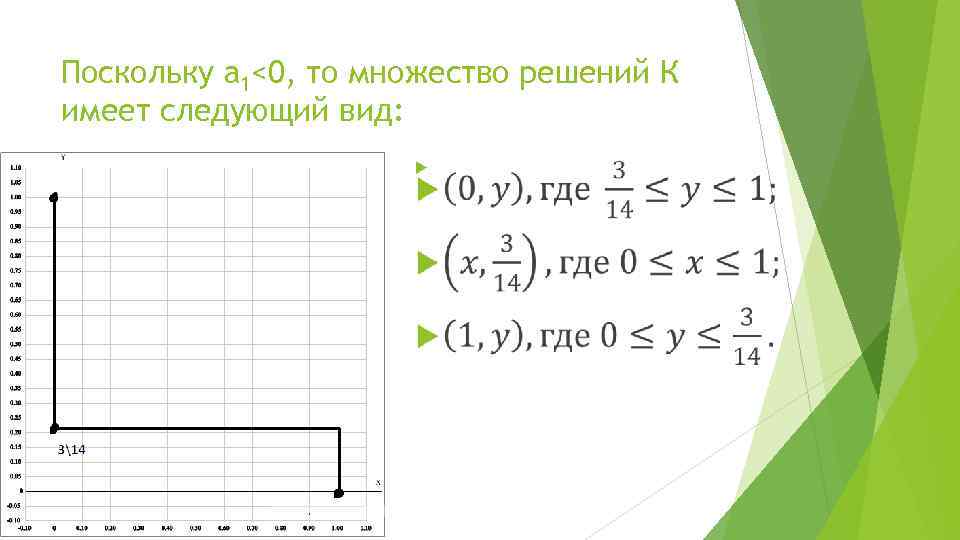
Поскольку а 1<0, то множество решений К имеет следующий вид:
Для второго игрока имеем:
Поскольку b 1>0, то множество L имеет следующий вид:
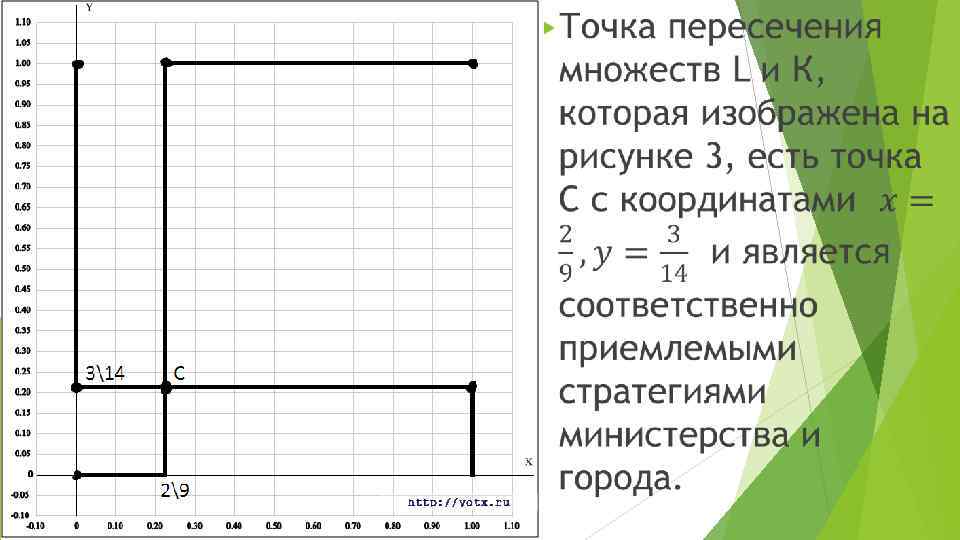
При этом выигрыш соответственно равен:
Таким образом мы получили данные:
Спасибо за внимание
Скачать презентацию Принципы решения биматричных игр Биматричные игры n m Биматричные
Презентация по теории игр.pptx