Принцип возможных перемещений 1 Пример

Принцип возможных перемещений 1

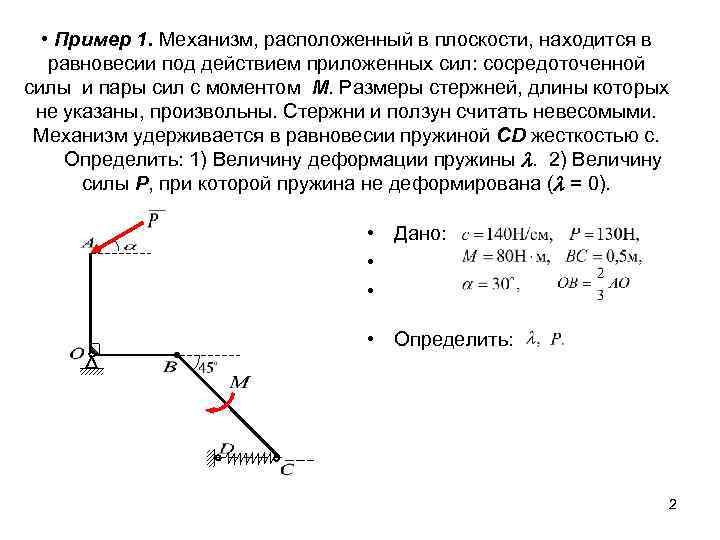• Пример 1. Механизм, расположенный в плоскости, находится в равновесии под действием приложенных сил: сосредоточенной силы и пары сил с моментом М. Размеры стержней, длины которых не указаны, произвольны. Стержни и ползун считать невесомыми. Механизм удерживается в равновесии пружиной СD жесткостью с. Определить: 1) Величину деформации пружины . 2) Величину силы Р, при которой пружина не деформирована ( = 0). • Дано: • • • Определить: 2

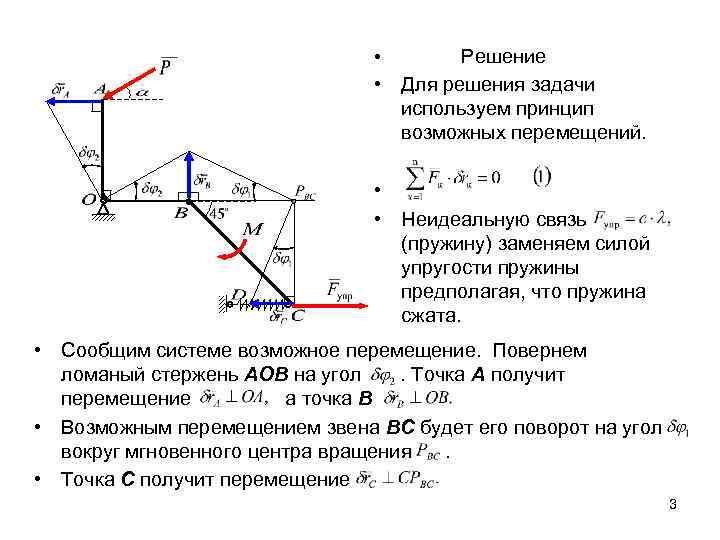Решение • Для решения задачи используем принцип возможных перемещений. • • • Неидеальную связь (пружину) заменяем силой упругости пружины предполагая, что пружина сжата. • Сообщим системе возможное перемещение. Повернем ломаный стержень АОВ на угол. Точка А получит перемещение а точка В • Возможным перемещением звена ВС будет его поворот на угол вокруг мгновенного центра вращения. • Точка С получит перемещение 3

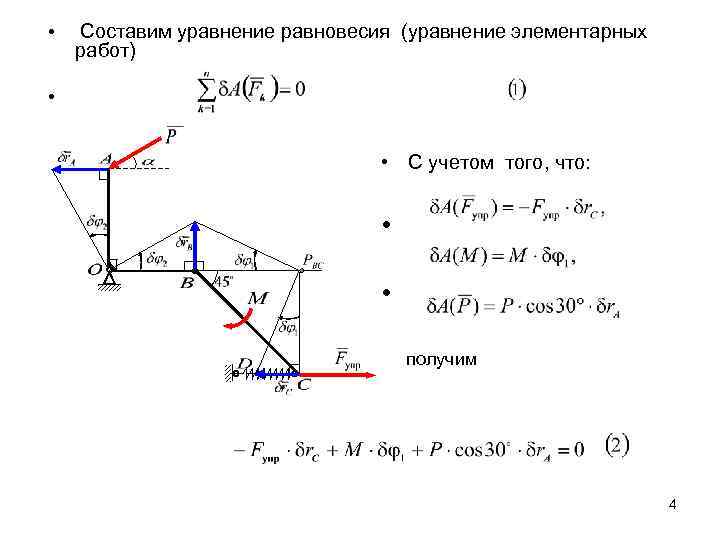• Составим уравнение равновесия (уравнение элементарных работ) • • С учетом того, что: • • получим 4

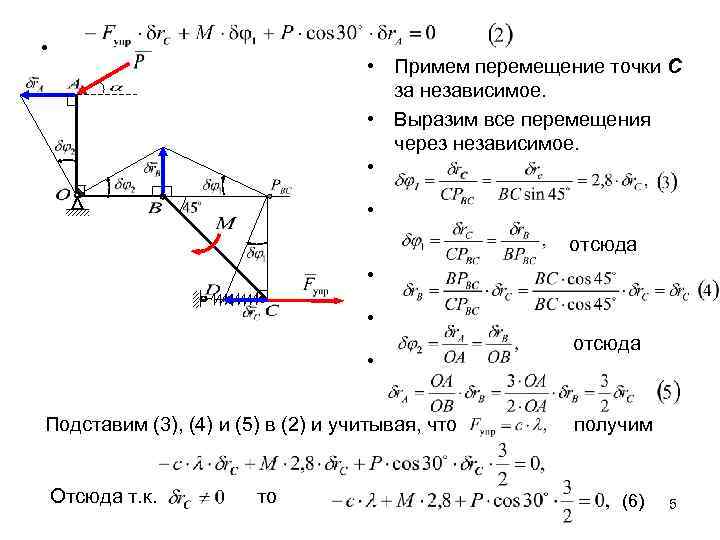• • Примем перемещение точки С за независимое. • Выразим все перемещения через независимое. • • отсюда • • • Подставим (3), (4) и (5) в (2) и учитывая, что Отсюда т. к. то отсюда получим (6) 5

• • Отсюда • • Знак “+” означает, что при таких нагрузках пружина действительно сжата. • 2) Определим силу при которой пружина не деформирована, т. е. • • Тогда из равенства • • Знак “-” говорит о том, что при таком направлении силы пружина будет деформирована при любом значении этой силы. 6

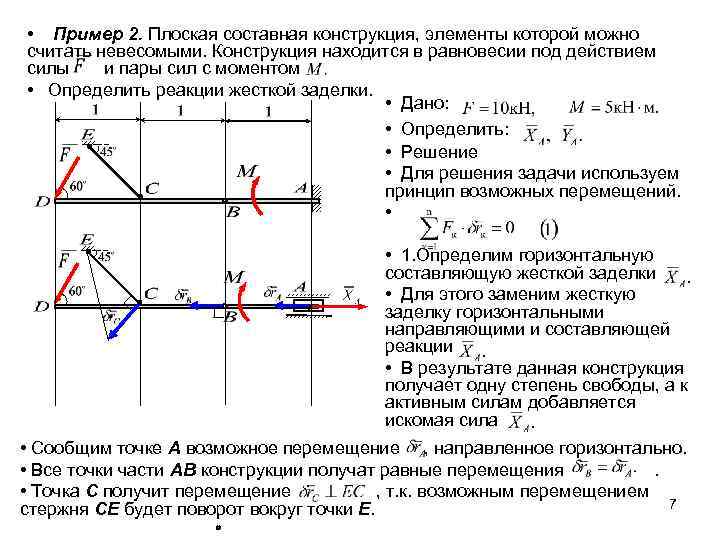• Пример 2. Плоская составная конструкция, элементы которой можно считать невесомыми. Конструкция находится в равновесии под действием силы и пары сил с моментом • Определить реакции жесткой заделки. • Дано: • Определить: • Решение • Для решения задачи используем принцип возможных перемещений. • • 1. Определим горизонтальную составляющую жесткой заделки • Для этого заменим жесткую заделку горизонтальными направляющими и составляющей реакции • В результате данная конструкция получает одну степень свободы, а к активным силам добавляется искомая сила • Сообщим точке А возможное перемещение , направленное горизонтально. • Все точки части АВ конструкции получат равные перемещения. • Точка С получит перемещение , т. к. возможным перемещением 7 стержня СЕ будет поворот вокруг точки Е.

• • • Возможным перемещением звена BCD будет поворот на угол вокруг мгновенного центра вращения (скоростей) (точка пересечения перпендикуляров к и , восстановленных из точек В и С). Точка D получит перемещение. Из возможных перемещений независимым от других может быть только одно (у механизма одна степень свободы). • • • Примем за независимое возможное перемещение и выразим через него все остальные перемещения. Т. к. с другой стороны Откуда Составим уравнение • • Здесь • по теореме Вариньона • т. к. (возможное движение АВ поступательное). 8

• Заменяя в уравнении скобки, получим его выражением через и, вынося за • • Т. к. • • • Из уравнения • • , то находим Т. к. Прямоугольный, то Подставим в численные значения Знак плюс “+” у полученного численного значения указывает на то, что выбранное направление соответствует реальному. 9

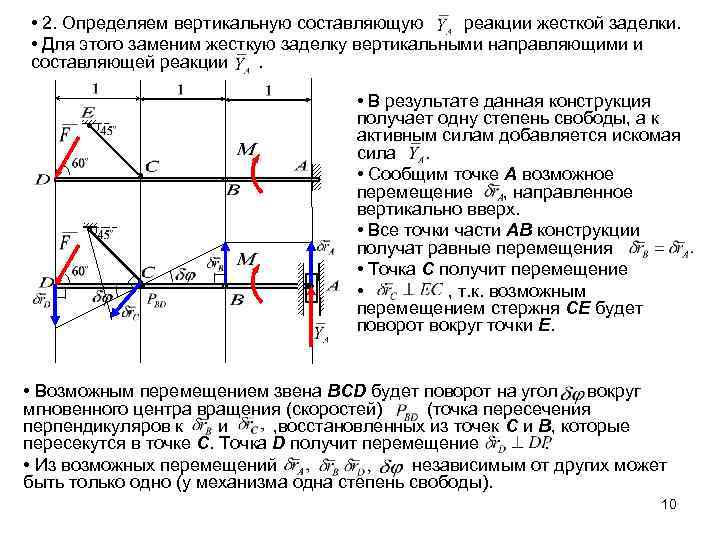• 2. Определяем вертикальную составляющую реакции жесткой заделки. • Для этого заменим жесткую заделку вертикальными направляющими и составляющей реакции. • В результате данная конструкция получает одну степень свободы, а к активным силам добавляется искомая сила • Сообщим точке А возможное перемещение , направленное вертикально вверх. • Все точки части АВ конструкции получат равные перемещения • Точка С получит перемещение • , т. к. возможным перемещением стержня СЕ будет поворот вокруг точки Е. • Возможным перемещением звена BCD будет поворот на угол вокруг мгновенного центра вращения (скоростей) (точка пересечения перпендикуляров к и , восстановленных из точек С и В, которые пересекутся в точке С. Точка D получит перемещение. • Из возможных перемещений независимым от других может быть только одно (у механизма одна степень свободы). 10

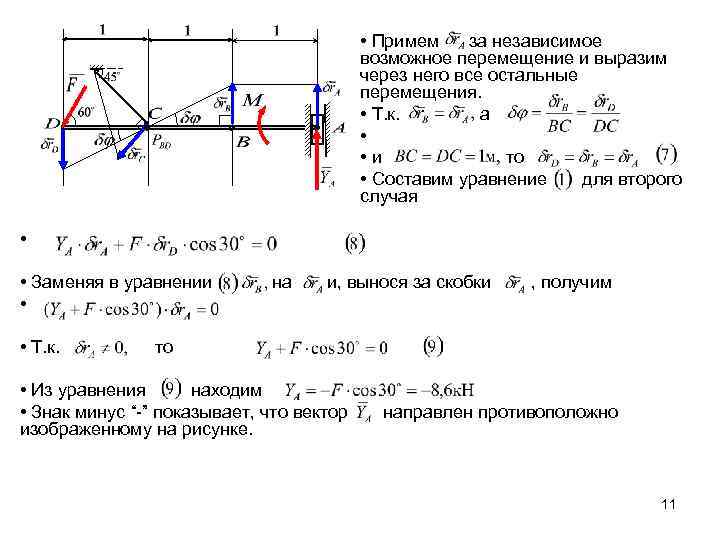• Примем за независимое возможное перемещение и выразим через него все остальные перемещения. • Т. к. а • • и то • Составим уравнение для второго случая • • Заменяя в уравнении • • Т. к. на и, вынося за скобки , получим то • Из уравнения находим • Знак минус “-” показывает, что вектор изображенному на рисунке. направлен противоположно 11

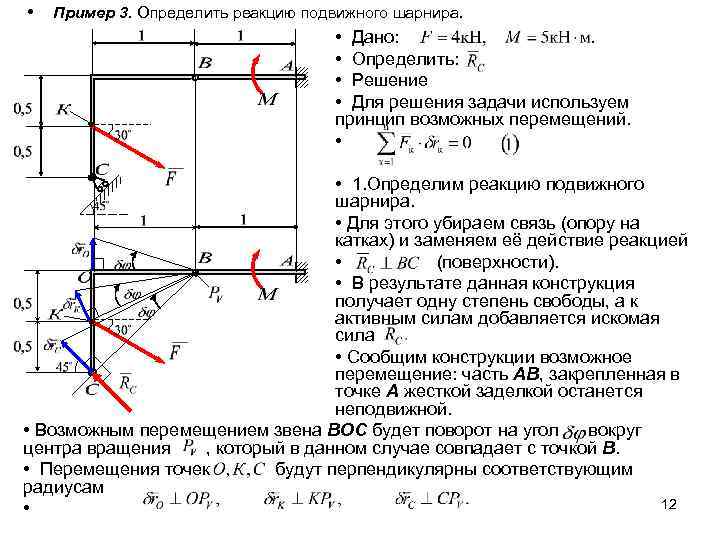• Пример 3. Определить реакцию подвижного шарнира. • Дано: • Определить: • Решение • Для решения задачи используем принцип возможных перемещений. • • 1. Определим реакцию подвижного шарнира. • Для этого убираем связь (опору на катках) и заменяем её действие реакцией • (поверхности). • В результате данная конструкция получает одну степень свободы, а к активным силам добавляется искомая сила • Сообщим конструкции возможное перемещение: часть АВ, закрепленная в точке А жесткой заделкой останется неподвижной. • Возможным перемещением звена ВОС будет поворот на угол вокруг центра вращения , который в данном случае совпадает с точкой В. • Перемещения точек будут перпендикулярны соответствующим радиусам 12 •

• Учитывая, что силы поворот, имеем • и приложены к телу, которому сообщен • По теореме Вариньона • • • Знак работы “+”, если направления поворота тела и момента силы относительно точки поворота совпадают. • т. к. • Составим уравнение , учитывая • • вынесем за скобки и получим • • Так как то • Откуда • С учетом того, что • найдем и . 13

• Пример 3. Определить реактивный момент. • Дано: D С • Определить: M • A В 1 1 • Решение 2 • Для решения задачи используем принцип возможных перемещений. • 60° • Определим реактивный момент жесткой заделки. • Для этого заделку заменим неподвижной шарнирной опорой и искомой парой сил • В результате данная конструкция получает одну степень свободы, а к активным нагрузкам (силе и паре ) добавляется искомая пара сил с моментом. • Сообщим конструкции возможное перемещение. • Повернем часть АВ на угол. Точка В получит перемещение. • Возможное перемещение точка С получит при повороте стержня • Возможным перемещением звена ВС будет поворот на угол вокруг центра вращения (точка пересечения перпендикуляров к и , восстановленных из точек В и С). Перемещения точек будут перпендикулярны соответствующим радиусам 14 •

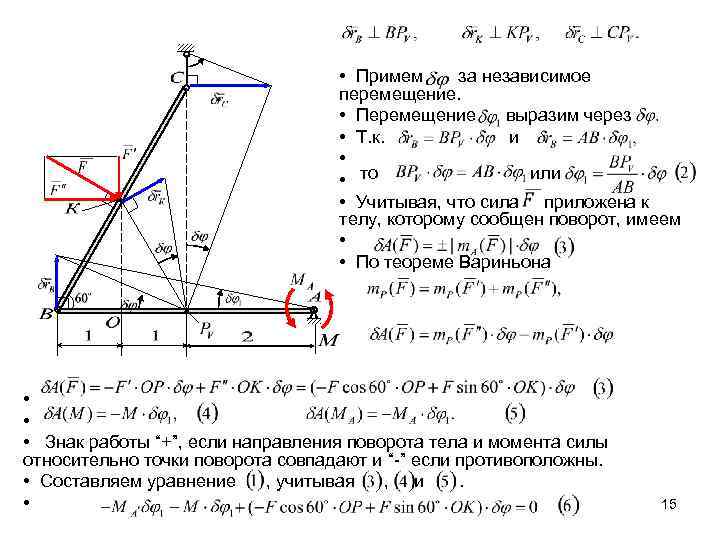• Примем за независимое перемещение. • Перемещение выразим через • Т. к. и • или • то • Учитывая, что сила приложена к телу, которому сообщен поворот, имеем • • По теореме Вариньона • • • Знак работы “+”, если направления поворота тела и момента силы относительно точки поворота совпадают и “-” если противоположны. • Составляем уравнение , учитывая , и. • 15

• Заменяя в уравнении скобки, получим его выражением через и, вынося за • • Т. к. • Из уравнения • • • Учтем, что • • то находим Т. к. прямоугольный, то Подставим в численные значения Знак плюс “+” у полученного численного значения указывает на то, что выбранное направление соответствует реальному. 16