ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ГАЛИЛЕЯ Лекция 7

ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ГАЛИЛЕЯ Лекция 7

• Согласно принципу относительности Галилея, любое механическое явление протекает одинаково во всех инерциальных системах отсчета. • Это означает, что никакими механическими опытами, проводимыми в инерциальной системе отсчета, нельзя установить. Движется ли эта система отсчета прямолинейно и равномерно или покоится. • Принципу относительности Галилея соответствуют преобразования координат Галилея.

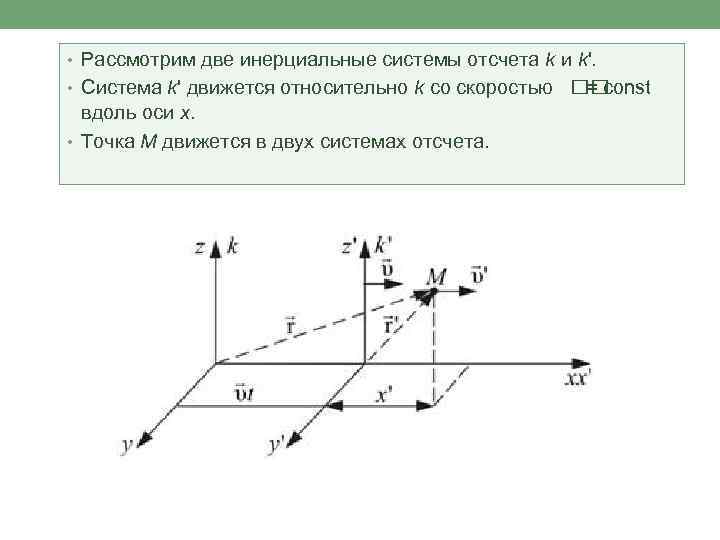• Рассмотрим две инерциальные системы отсчета k и k'. • Система k' движется относительно k со скоростью = const вдоль оси x. • Точка М движется в двух системах отсчета.

• Найдем связь между координатами точки M в обеих системах отсчета. Отсчет начнем, когда начала координат систем совпадают, то есть t = t'. • Совокупность этих уравнений называется преобразованиями Галилея

• В векторной форме преобразования Галилея можно записать так: Продифференцируем это выражение по времени, получим: или (1) Выражение (1) определяет закон сложения скоростей в классической механике. Из него следует, что скорость движения точки М (сигнала) в системе k' и в системе k различна.

• Преобразования Галилея позволяют по известным координатам и времени некоторого события в одной инерциальной системе отсчета, найти координаты и время этого же события в другой инерциальной системе, движущейся относительно первой с некоторой скоростью . • Уравнения классической механики инвариантны относительно преобразований Галилея. • Физические величины, которые при преобразованиях Галилея остаются неизменными, называются инвариантами преобразований Галилея. • Ускорение является инвариантом преобразований Галилея: а = а’.

•