 Принцип Гюйгенса. Закон отражения света.
Принцип Гюйгенса. Закон отражения света.
 Законы отражения и преломления света можно вывести из одного общего принципа, который был впервые выдвинут современником Ньютона, приверженцем волновой теории света Христианом Гюйгенсом…
Законы отражения и преломления света можно вывести из одного общего принципа, который был впервые выдвинут современником Ньютона, приверженцем волновой теории света Христианом Гюйгенсом…
 Принцип Гюйгенса позволяет описывать поведение волн любой природы, но особенно наглядное истолкование принципа - для частиц среды, создающих механические волны… Христиан Гюйгенс 1629 -1695
Принцип Гюйгенса позволяет описывать поведение волн любой природы, но особенно наглядное истолкование принципа - для частиц среды, создающих механические волны… Христиан Гюйгенс 1629 -1695
 Принцип Гюйгенса: «Каждая точка среды, до которой дошло возмущение, сама становится источником вторичных волн. »
Принцип Гюйгенса: «Каждая точка среды, до которой дошло возмущение, сама становится источником вторичных волн. »
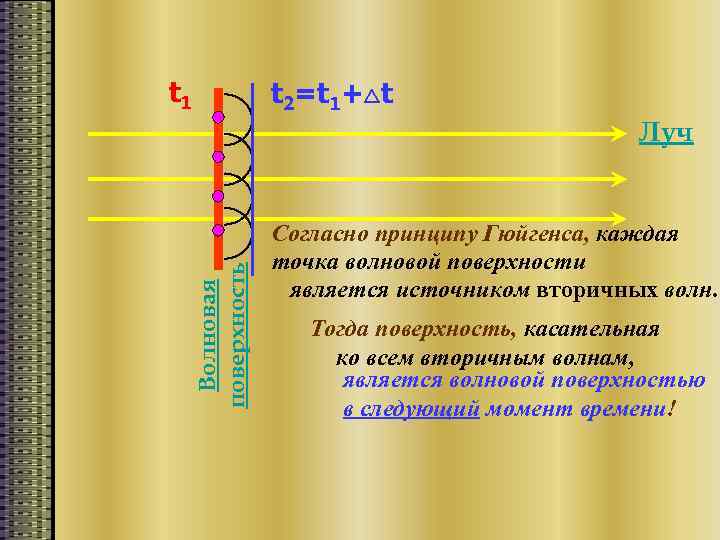 t 1 t 2=t 1+ t Волновая поверхность Луч Согласно принципу Гюйгенса, каждая точка волновой поверхности является источником вторичных волн. Тогда поверхность, касательная ко всем вторичным волнам, является волновой поверхностью в следующий момент времени!
t 1 t 2=t 1+ t Волновая поверхность Луч Согласно принципу Гюйгенса, каждая точка волновой поверхности является источником вторичных волн. Тогда поверхность, касательная ко всем вторичным волнам, является волновой поверхностью в следующий момент времени!
 Принцип Гюйгенса описывает распространение волн любой природы, в том числе и световых. Посмотрите, как изящно выводится закон отражения света с помощью принципа Гюйгенса:
Принцип Гюйгенса описывает распространение волн любой природы, в том числе и световых. Посмотрите, как изящно выводится закон отражения света с помощью принципа Гюйгенса:
 Пусть на границу раздела двух сред падает плоская световая волна.
Пусть на границу раздела двух сред падает плоская световая волна.
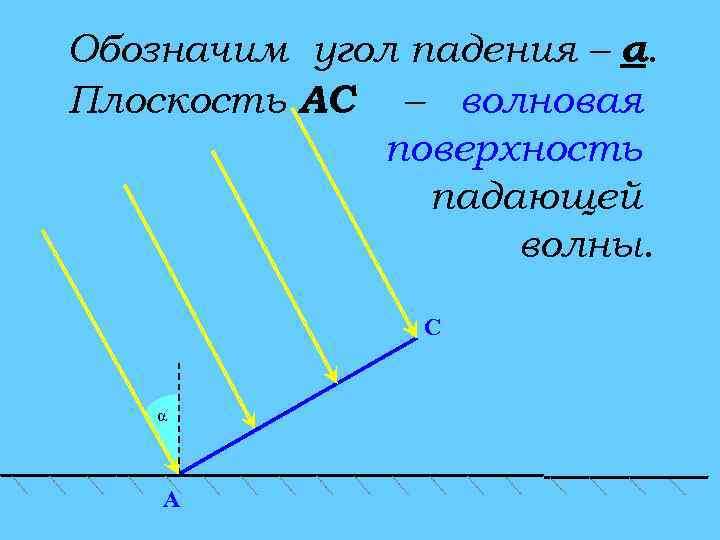 Обозначим угол падения – α. Плоскость АС – волновая поверхность падающей волны. C α A
Обозначим угол падения – α. Плоскость АС – волновая поверхность падающей волны. C α A
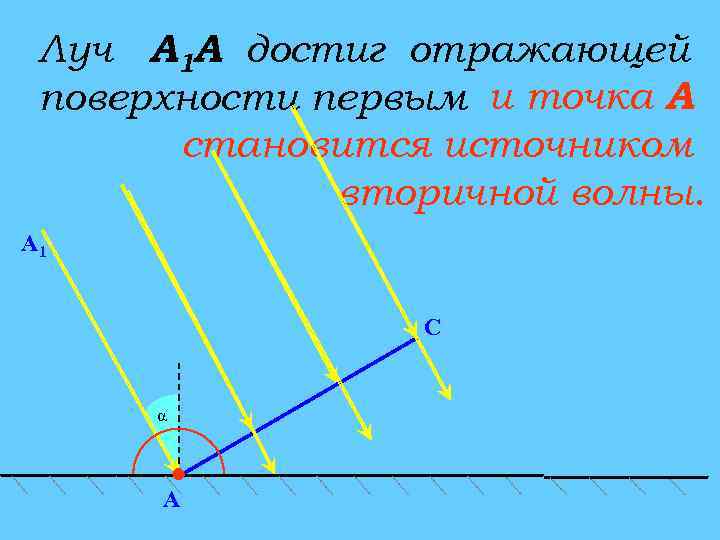 Луч А 1 А достиг отражающей поверхности первым и точка А становится источником вторичной волны. А 1 C α A
Луч А 1 А достиг отражающей поверхности первым и точка А становится источником вторичной волны. А 1 C α A
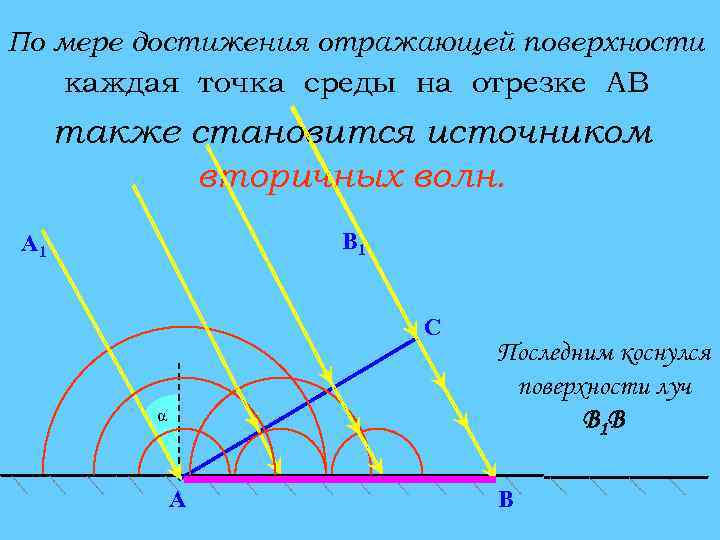 По мере достижения отражающей поверхности каждая точка среды на отрезке АВ также становится источником вторичных волн. В 1 А 1 C α A Последним коснулся поверхности луч В 1 В В
По мере достижения отражающей поверхности каждая точка среды на отрезке АВ также становится источником вторичных волн. В 1 А 1 C α A Последним коснулся поверхности луч В 1 В В
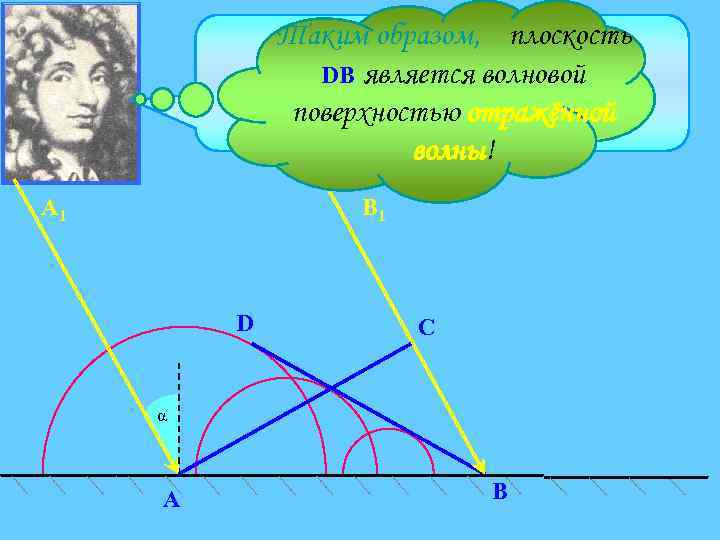 Таким образом, плоскость Поверхность, касательная ко всем вторичным волнам, DB является волновой поверхностью в поверхностью отражённой следующий момент времени. волны! А 1 В 1 D C α A В
Таким образом, плоскость Поверхность, касательная ко всем вторичным волнам, DB является волновой поверхностью в поверхностью отражённой следующий момент времени. волны! А 1 В 1 D C α A В
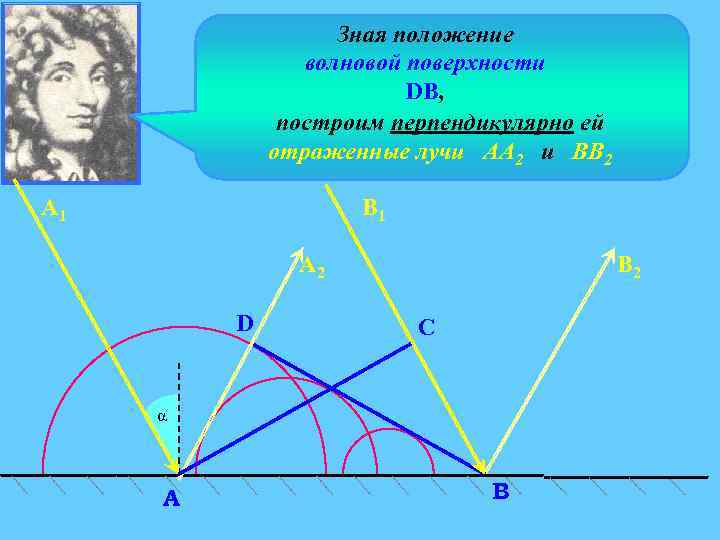 Зная положение волновой поверхности DB, построим перпендикулярно ей отраженные лучи АА 2 и ВВ 2 А 1 В 1 А 2 D В 2 C α A В
Зная положение волновой поверхности DB, построим перпендикулярно ей отраженные лучи АА 2 и ВВ 2 А 1 В 1 А 2 D В 2 C α A В
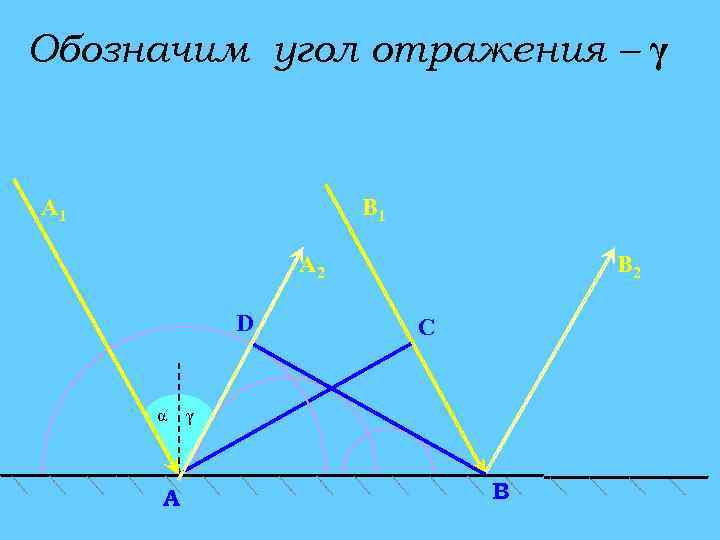 Обозначим угол отражения – γ А 1 В 1 А 2 D α A В 2 C γ В
Обозначим угол отражения – γ А 1 В 1 А 2 D α A В 2 C γ В
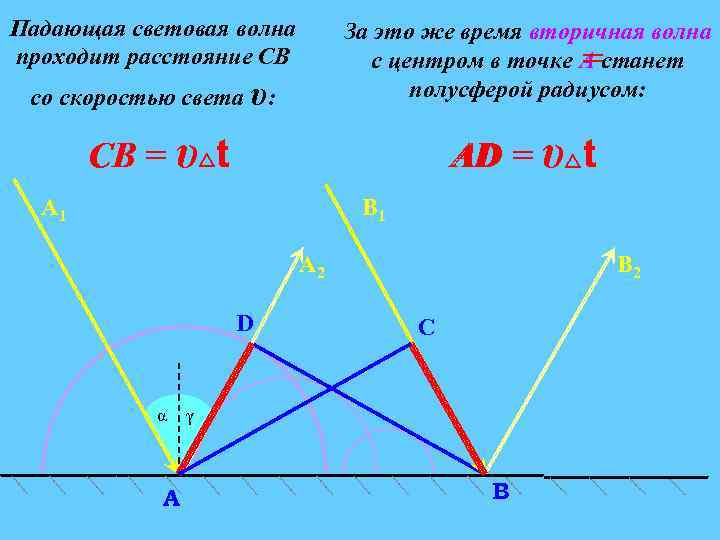 Падающая световая волна проходит расстояние СВ со скоростью света υ: За это же время вторичная волна с центром в точке А станет = полусферой радиусом: СВ = υ t АD = υ t А 1 В 1 А 2 D α A В 2 C γ В
Падающая световая волна проходит расстояние СВ со скоростью света υ: За это же время вторичная волна с центром в точке А станет = полусферой радиусом: СВ = υ t АD = υ t А 1 В 1 А 2 D α A В 2 C γ В
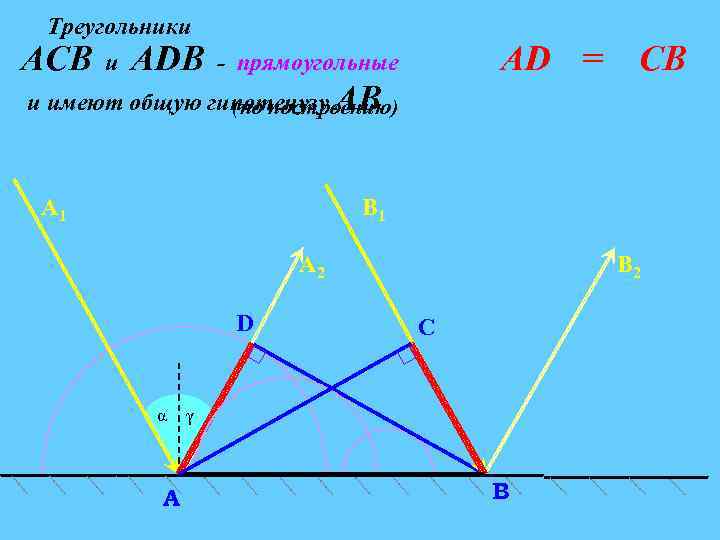 Треугольники АСВ и АDВ АD = - прямоугольные и имеют общую гипотенузу АВ (по построению) А 1 СВ В 1 А 2 D α A В 2 C γ В
Треугольники АСВ и АDВ АD = - прямоугольные и имеют общую гипотенузу АВ (по построению) А 1 СВ В 1 А 2 D α A В 2 C γ В
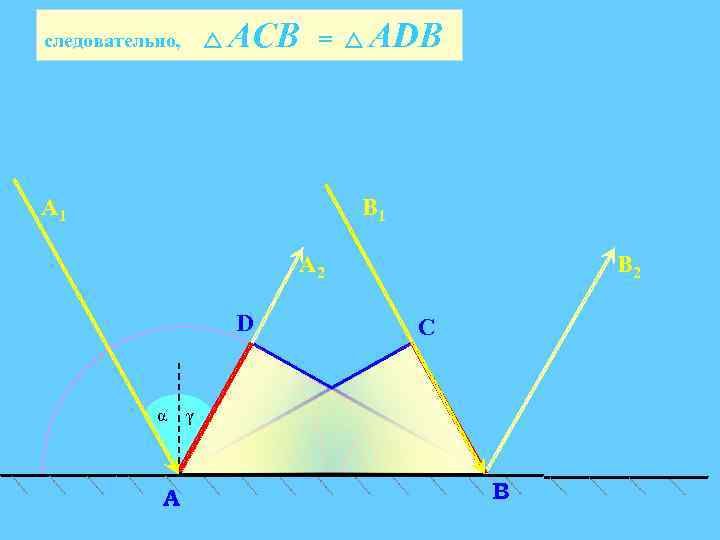 следовательно, АСВ = АDВ А 1 В 1 А 2 D α A В 2 C γ В
следовательно, АСВ = АDВ А 1 В 1 А 2 D α A В 2 C γ В
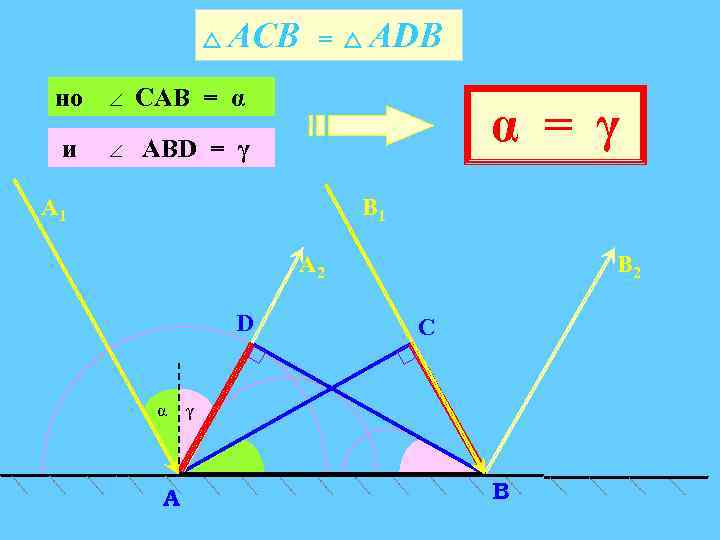 АСВ но САВ = α и = АDВ АВD = γ α = γ А 1 В 1 А 2 D α A В 2 C γ В
АСВ но САВ = α и = АDВ АВD = γ α = γ А 1 В 1 А 2 D α A В 2 C γ В
 Итак: Кроме того, из построения следует: α γ α = γ Падающий луч, луч отражённый и перпендикуляр, восстановленный в точке падения луча к границе раздела двух сред, лежат в одной плоскости.
Итак: Кроме того, из построения следует: α γ α = γ Падающий луч, луч отражённый и перпендикуляр, восстановленный в точке падения луча к границе раздела двух сред, лежат в одной плоскости.